Soru Sor sayfası kullanılarak Üçgende Kenarortay konusu altında Muhteşem üçlü, Dik üçgende kenarortay ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
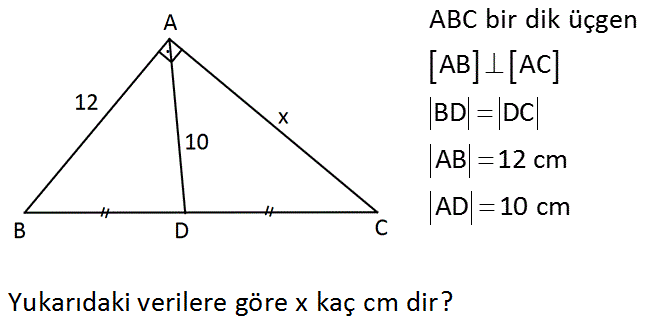

2.SORU
3.SORU

4.SORU
5.SORU
6.SORU
7.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net ABC bir dik üçgen AB AC BD DC AB 12 cm AD 10 cm Yukarıdaki verilere göre x kaç cm dir? Çözüm: Dik üçgende kenarortay eş bölünen tabanlara eşittir. (muhteşem üçlü) AD BD DC 10 cm ABC üçgeninin kenarları 3 – 4 – 5 üçgeninin 4 katıdır. Buradan x 16 cm bulunur. 3
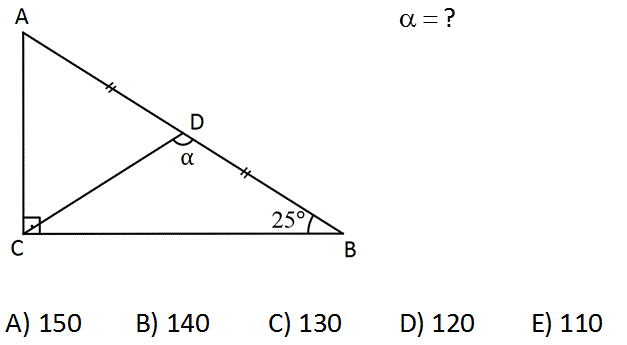
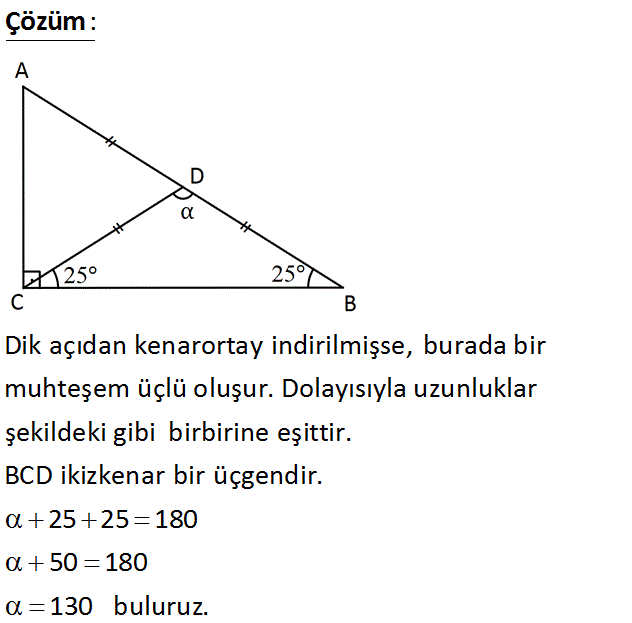
? A) 150 B) 140 C) 130 D) 120 E) 110 www.matematikkolay.net : Çözüm Dik açıdan kenarortay indirilmişse, burada bir muhteşem üçlü oluşur. Dolayısıyla uzunluklar şekildeki gibi birbirine eşittir. BCD ikizkenar bir üçgendir. 25 25 180 50 180 130 buluruz. 4
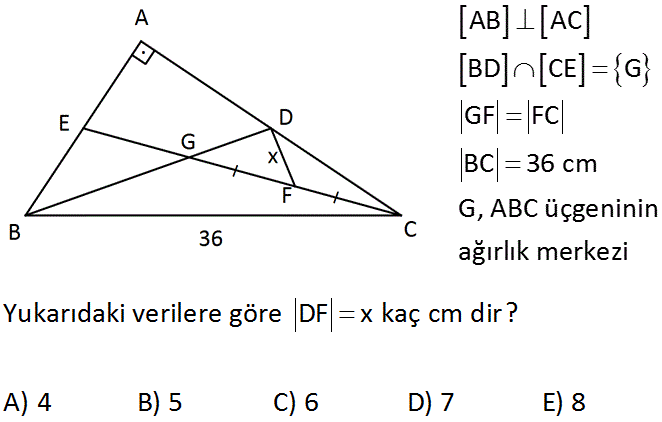
AB AC BD CE G GF FC BC 36 cm G, ABC üçgeninin ağırlık merkezi Yukarıdaki verilere göre DF x kaç cm dir? A) 4 B) 5 C) 6 D) 7 E) 8 Çözüm: www.matematikkolay.net Dik üçgende kenarortay uzunluğu muhteşem üçlü oluşturur. Kenarortay 2k ya k bölünür. ACG üçgenine dikkat edilirse DF uzunluğu iki kenarı da eş bölmüş. O halde DF orta tabandır. 12 DF 6 cm bulunur. 2 8
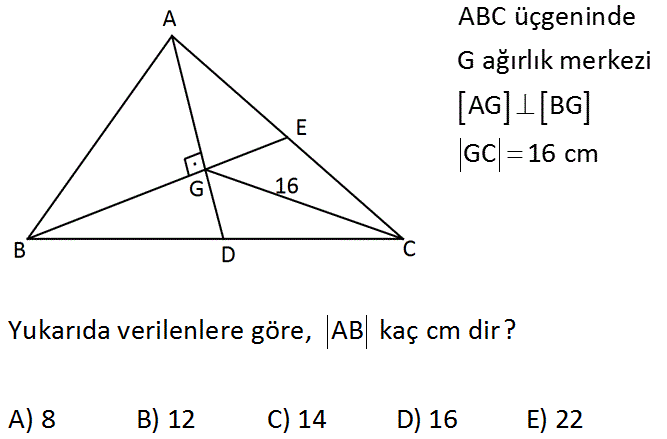
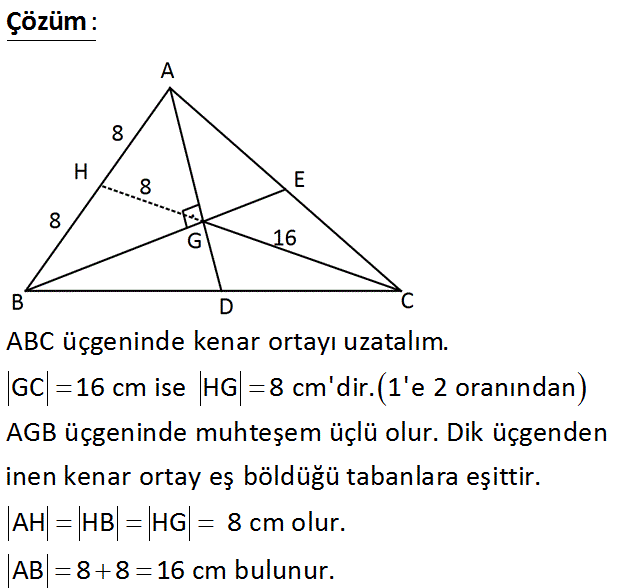
ABC üçgeninde G ağırlık merkezi AG BG GC 16 cm Yukarıda verilenlere göre, AB kaç cm dir? A) 8 B) 12 C) 14 D) 16 E) 22 Çözüm: www.matematikkolay.net ABC üçgeninde kenar ortayı uzatalım. GC 16 cm ise HG 8 cm’dir. 1’e 2 oranından AGB üçgeninde muhteşem üçlü olur. Dik üçgenden inen kenar ortay eş böldüğü tabanlara eşittir. AH HB HG 8 cm olur. AB 8 8 16 cm bulunur. 14
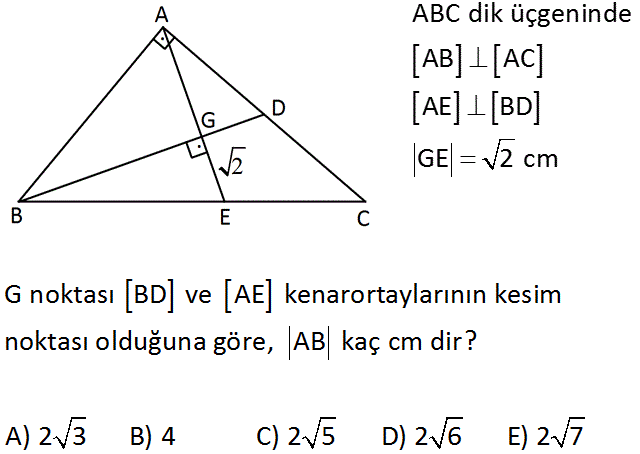
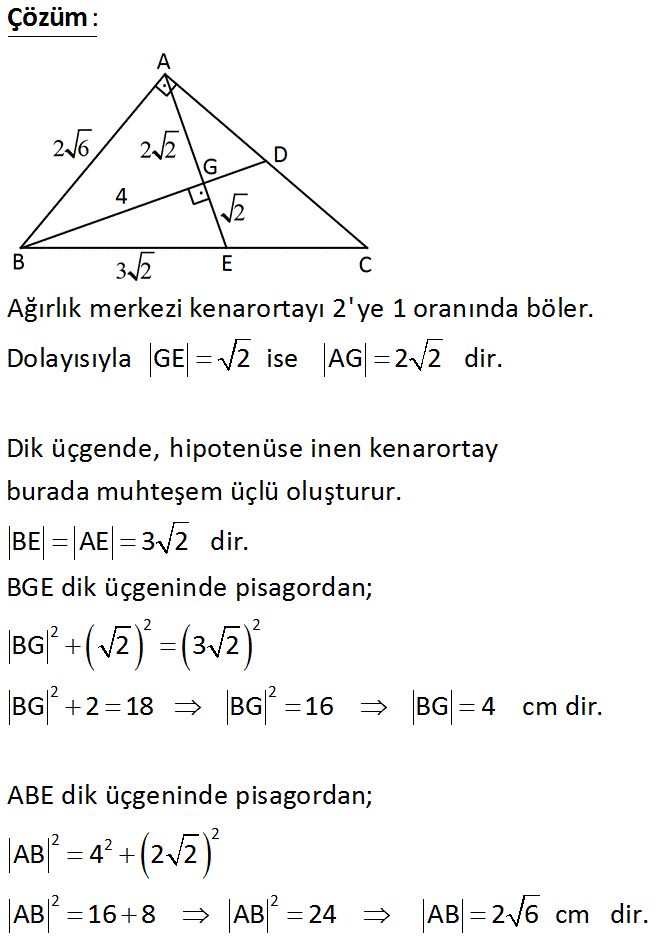
ABC dik üçgeninde AB AC AE BD GE 2 cm G noktası BD ve AE kenarortaylarının kesim noktası olduğuna göre, AB kaç cm dir? A) 2 3 B) 4 C) 2 5 D) 2 6 E) 2 7 www.matematikkolay.net : Çözüm Ağırlık merkezi kenarortayı 2′ ye 1 oranında böler. Dolayısıyla GE 2 ise AG 2 2 dir. Dik üçgende, hipotenüse inen kenarortay burada muhteşem üçlü oluşturur. BE AE 3 2 dir. BGE dik üçgeninde pisagord 2 2 2 2 2 2 2 2 2 2 an; BG 2 3 2 BG 2 18 BG 16 BG 4 cm dir. ABE dik üçgeninde pisagordan; AB 4 2 2 AB 16 8 AB 24 AB 2 6 cm dir. 20
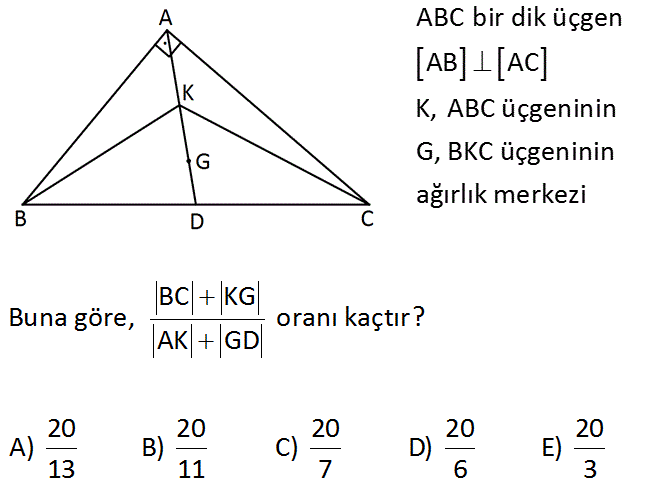
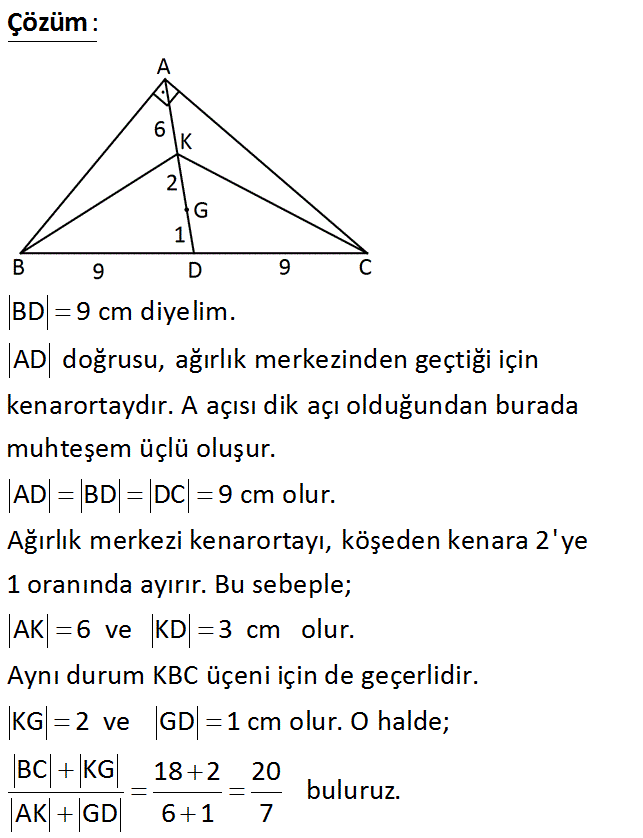
ABC bir dik üçgen AB AC K, ABC üçgeninin G, BKC üçgeninin ağırlık merkezi BC KG Buna göre, oranı kaçtır? AK GD 20 20 20 20 20 A) B) C) D) E) 13 11 7 6 3 Çözüm: www.matematikkolay.net BD 9 cm diyelim. AD doğrusu, ağırlık merkezinden geçtiği için kenarortaydır. A açısı dik açı olduğundan burada muhteşem üçlü oluşur. AD BD DC 9 cm olur. Ağırlık merkezi kenarortayı, köşeden kenara 2’ye 1 or anında ayırır. Bu sebeple; AK 6 ve KD 3 cm olur. Aynı durum KBC üçeni için de geçerlidir. KG 2 ve GD 1 cm olur. O halde; BC KG 18 2 20 buluruz. AK GD 6 1 7 23
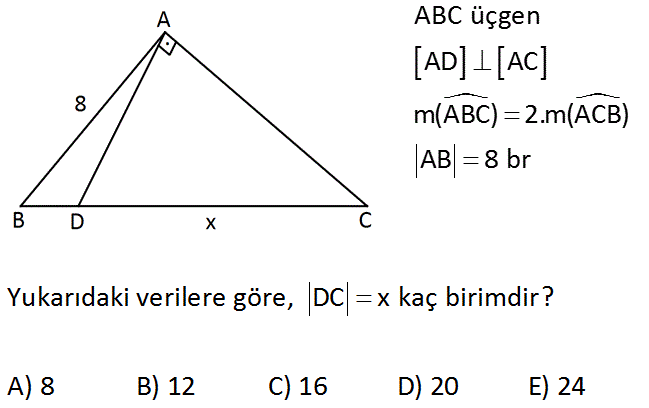
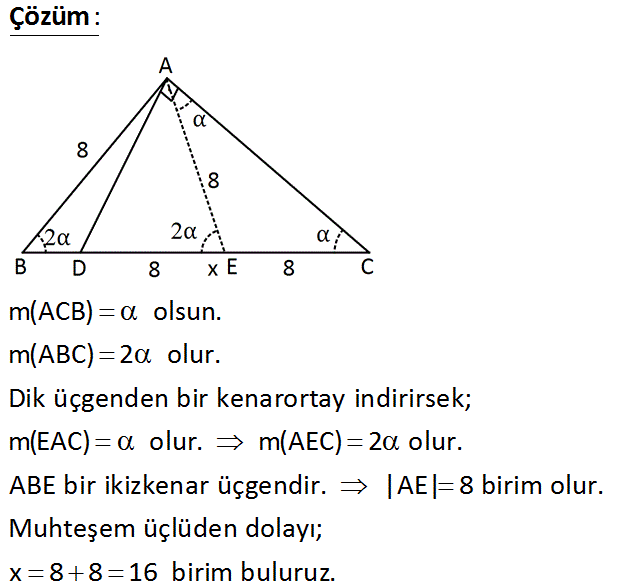
ABC üçgen AD AC m(ABC) 2.m(ACB) AB 8 br Yukarıdaki verilere göre, DC x kaç birimdir? A) 8 B) 12 C) 16 D) 20 E) 24 : Çözüm m(ACB) olsun. m(ABC) 2 olur. Dik üçgenden bir kenarortay indirirsek; m(EAC) olur. m(AEC) 2 olur. ABE bir ikizkenar üçgendir. |AE| 8 birim olur. Muhteşem üçlüden dolayı; x 8 8 16 birim buluruz. www.matematikkolay.net 26

