Soru Sor sayfası kullanılarak Üçgende Kenarortay konusu altında Kenarortay Formülü, Kenarortay Uzunluğu ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

2.SORU

3.SORU
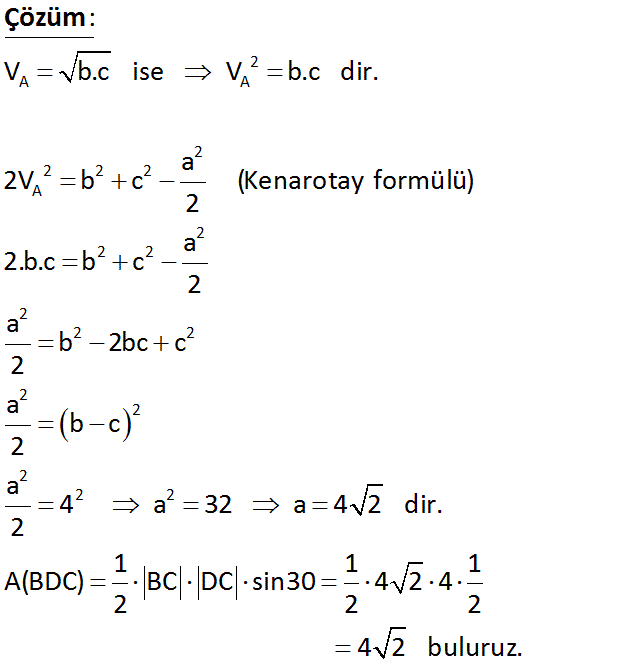
4.SORU
5.SORU

6.SORU

7.SORU
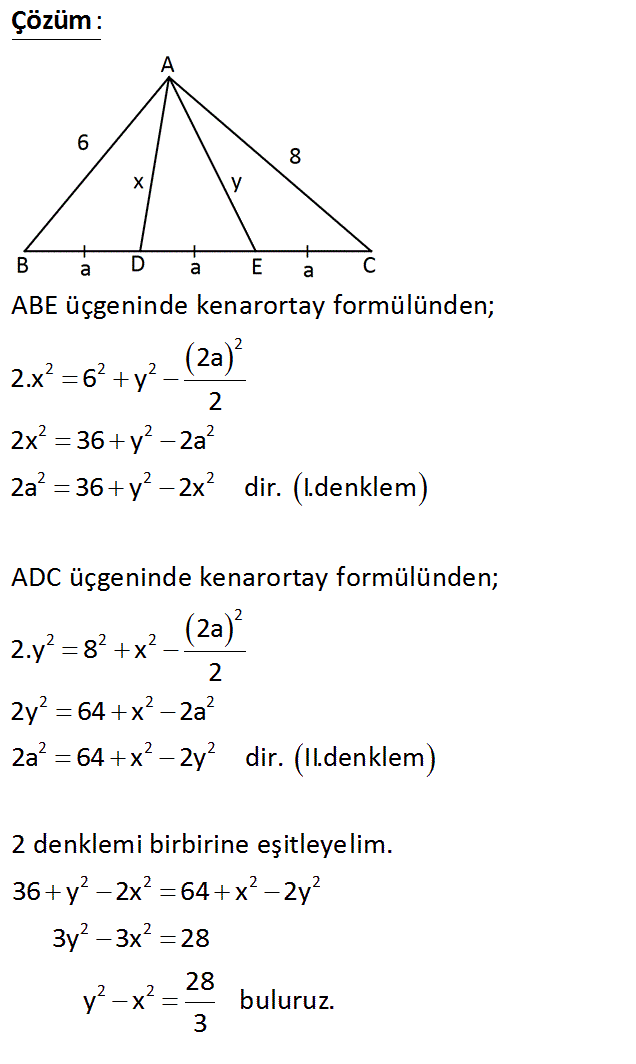
8.SORU
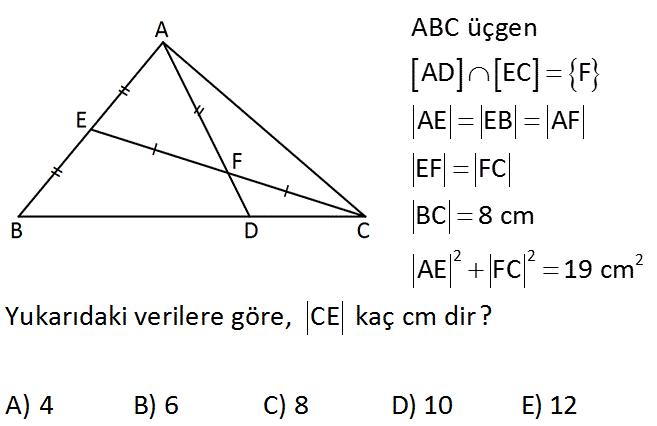

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
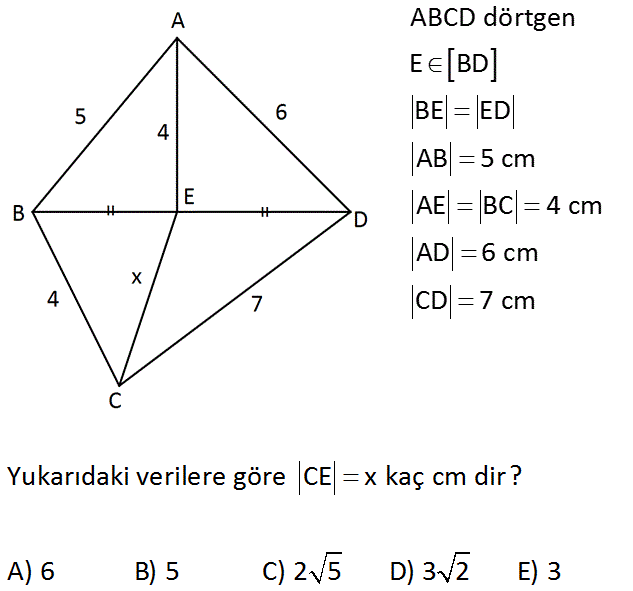
ABCD dörtgen E BD BE ED AB 5 cm AE BC 4 cm AD 6 cm CD 7 cm Yukarıdaki verilere göre CE x kaç cm dir? A) 6 B) 5 C) 2 5 D) 3 2 E) 3 www.matematikkolay.net 2 2 2 2 A 2 2 2 2 2 2 2 a 2b c (Kenarotay formülü) 2 Buna göre; (ABD üçgenindeki kenarortaya göre) a a 2.4 5 6 32 25 36 2 2 a a 32 61 29 dur. 2 2 Şimdi BCD üçg : enin Çözüm 2 2 2 2 2 deki kenarortayı bulalım. a 2 x 16 49 2 2 x 16 49 29 2 x 36 x 18 x 3 2 buluruz. 6
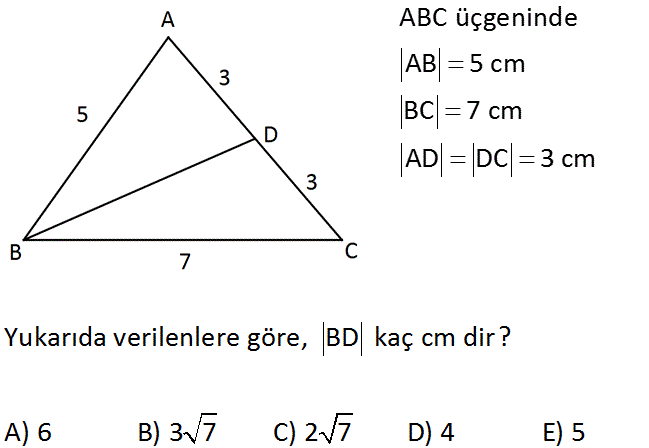
ABC üçgeninde AB 5 cm BC 7 cm AD DC 3 cm Yukarıda verilenlere göre, BD kaç cm dir? A) 6 B) 3 7 C) 2 7 D) 4 E) 5 www.matematikkolay.net b 2 2 2 2 b 2 2 2 2 b 2 b 2 b 2 b 2 b b B’den AC ‘ ye inen kenarortayın uzunluğu BD ‘dir. b 2a c 2 6 27 5 2 249 25 18 274 18 256 56 28 2 28 2 7 bulunur : . Çözüm 15
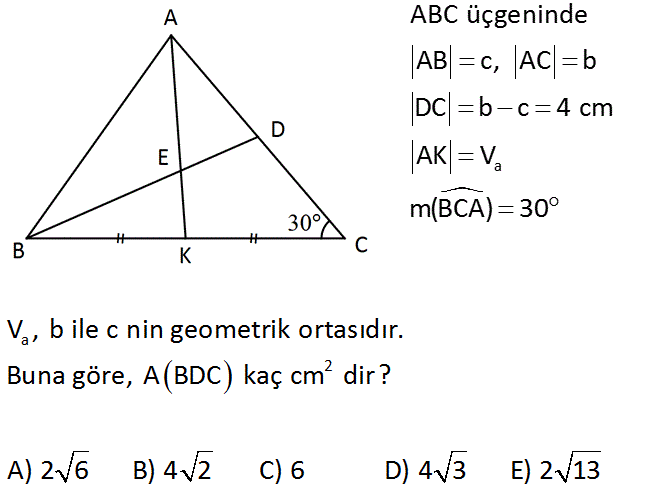
a ABC üçgeninde AB c, AC b DC b c 4 cm AK m(BCA) 30 a 2 , b ile c nin geometrik ortasıdır. Buna göre, A BDC kaç cm dir? A) 2 6 B) 4 2 C) 6 D) 4 3 E) 2 13 www.matematikkolay.net 2 A A 2 2 2 2 A 2 2 2 2 2 2 2 2 2 2 2 b.c ise b.c dir. a 2b c (Kenarotay formülü) 2 a 2.b.c b c 2 a b 2bc c 2 a b c 2 a 4 a 32 a 4 2 dir. 2 1 1 1 A(BDC) BC DC sin30 4 2 4 2 2 2 : Çözüm 4 2 buluruz. 17
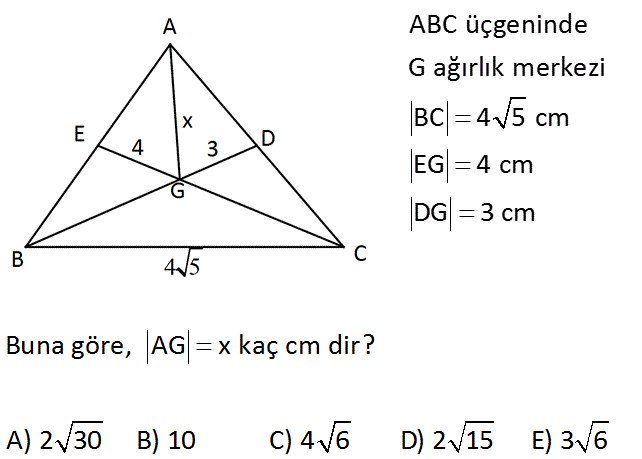
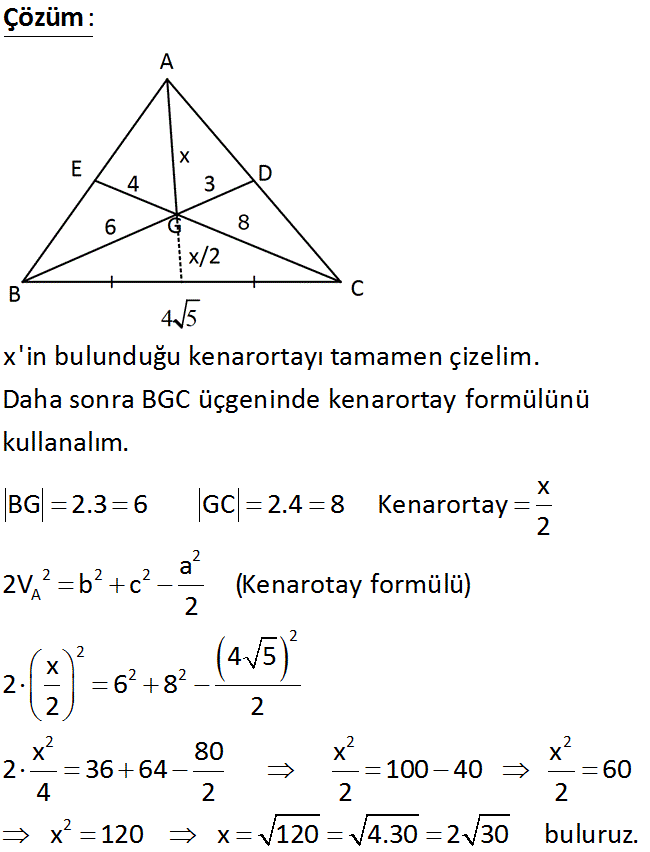
ABC üçgeninde G ağırlık merkezi BC 4 5 cm EG 4 cm DG 3 cm Buna göre, AG x kaç cm dir? A) 2 30 B) 10 C) 4 6 D) 2 15 E) 3 6 www.matematikkolay.net : Çözüm 2 2 2 2 A 2 2 2 2 x’in bulunduğu kenarortayı tamamen çizelim. Daha sonra BGC üçgeninde kenarortay formülünü kullanalım. x BG 2.3 6 GC 2.4 8 Kenarortay 2 a 2b c (Kenarotay formülü) 2 x 4 5 2 6 8 2 2 2 2 2 2 x 80 x x 2 36 64 100 40 60 4 2 2 2 x 120 x 120 4.30 2 30 buluruz. 19
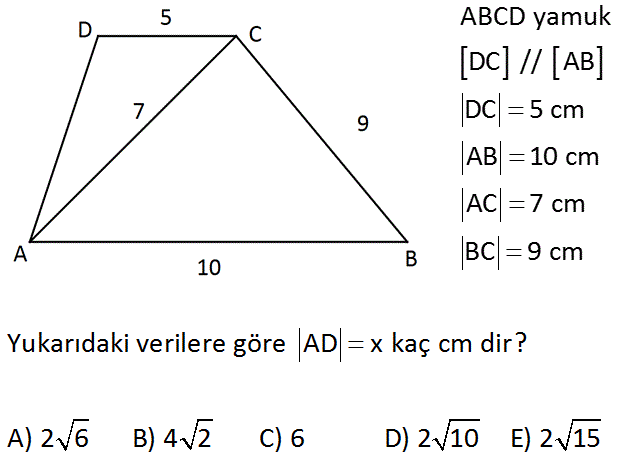
ABCD yamuk DC // AB DC 5 cm AB 10 cm AC 7 cm BC 9 cm Yukarıdaki verilere göre AD x kaç cm dir? A) 2 6 B) 4 2 C) 6 D) 2 10 E) 2 15 Çözüm: www.matematikkolay.net 2 2 2 2 2 2 2 C köşesinden, [AD] ye paralel indirirsek; bu doğru tabanı 5 ve 5 olarak ikiye ayırır. Demek ki bu bir kenarortaymış. Kenarortay uzunluğunu formülle bulalım. 10 2x 7 9 2 2x 49 81 50 2x 80 x 40 x 2 10 b uluruz. 7
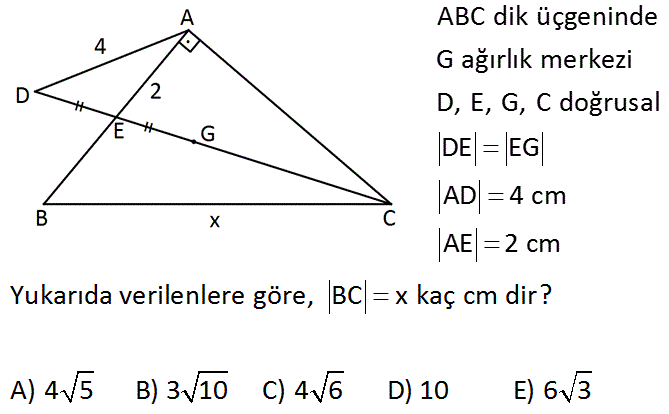
ABC dik üçgeninde G ağırlık merkezi D, E, G, C doğrusal DE EG AD 4 cm AE 2 cm www.matematikkolay.net Yukarıda verilenlere göre, BC x kaç cm dir? A) 4 5 B) 3 10 C) 4 6 D) 10 E) 6 3 : Çözüm 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 DAG üçgeninde kenarortay formülünden; 2a 2.2 16 4k 2 8 16 4k 2a 2a 4k 16 8 2a 4k 8 a 2k 4 olur. Bu cepte AEC üçgeninde pisagordan; AC 3a 2 9a 4 tür. ABC üçgeninde pisagordan; 4 AC 6k 16 9 2 2 2 2 2 2 2 2 2 2 2 2 2 2 a 4 36k 9a 12 36k a yerine 2k 4 yazalım. 9 2k 4 12 36k 18k 36 12 36k 18k 48 36k 48 18k 2 ile çarpalım. 96 36k karekök alalım. 4 6 6k x 4 6 cm buluruz. www.matematikkolay.net 21
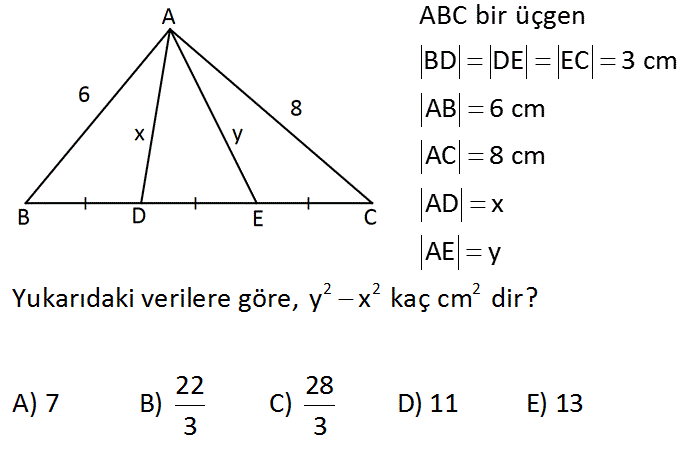
ABC bir üçgen BD DE EC 3 cm AB 6 cm AC 8 cm AD x AE y 2 2 2 Yukarıdaki verilere göre, y x kaç cm dir? 22 28 A) 7 B) C) D) 11 E) 13 3 3 www.matematikkolay.net : Çözüm 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ABE üçgeninde kenarortay formülünden; 2a 2.x 6 y 2 2x 36 y 2a 2a 36 y 2x dir. I.denklem ADC üçgeninde kenarortay formülünden; 2a 2.y 8 x 2 2y 64 x 2a 2a 64 x 2y dir. II.denklem 2 denkl 2 2 2 2 2 2 2 2 emi birbirine eşitleyelim. 36 y 2x 64 x 2y 3y 3x 28 28 y x buluruz. 3 24
2 2 2 ABC üçgen AD EC F AE EB AF EF FC BC 8 cm AE FC 19 cm Yukarıdaki verilere göre, CE kaç cm dir? A) 4 B) 6 C) 8 D) 10 E) 12 Çözüm: www.matematikkolay.net 2 2 2 2 2 2 a 2 2 2 2 2 2 2 2 2 2 2 2 2.19 38 2 2 b a 19 a Kenarortay Formülü:2b c 2 AEC üçgeninde kenarortay formülü uygulayalım. 2a 2.b b AC 2 2b b AC 2a AC 2a 2b b AC 38 b … 1 ABC üçgeninde kenarortay formülü uygulayalım 2 2 2 2 2 2 2 2 2 2 2 2 2 2 38 2 2 2 2 2 2 2 2 2 2 2 19 2 2 . 2b 2. 2a AC 8 2 8a AC 64 2b AC 8a 2b 64 AC 6a 2a 2b 64 AC 6a 38 64 AC 6a 26 ….. 2 1 ve 2 yi eşitleyelim. 38 b 6a 26 64 6a b 64 a b 5a 5a 45 a 9 a 3 CE 2a 6 cm bulunur. 27

