Soru Sor sayfası kullanılarak Üçgende Kenarortay konusu altında Ağırlık Merkezi ve Orta Taban ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU

3.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
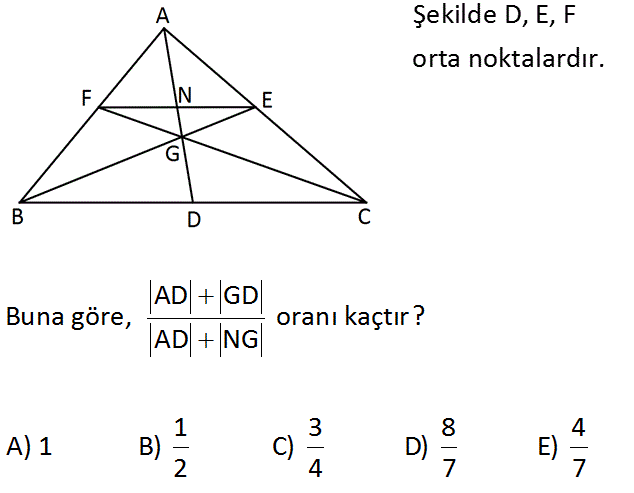
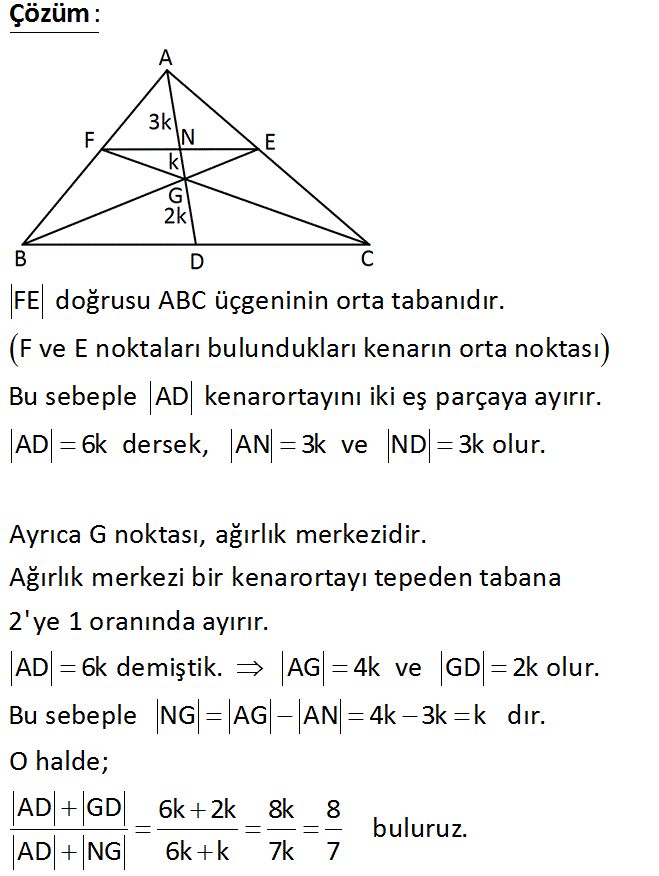
Şekilde D, E, F orta noktalardır. AD GD Buna göre, oranı kaçtır? AD NG 1 3 8 4 A) 1 B) C) D) E) 2 4 7 7 : Çözüm www.matematikkolay.net FE doğrusu ABC üçgeninin orta tabanıdır. F ve E noktaları bulundukları kenarın orta noktası Bu sebeple AD kenarortayını iki eş parçaya ayırır. AD 6k dersek, AN 3k ve ND 3k olur. Ayrıca G noktası, ağır lık merkezidir. Ağırlık merkezi bir kenarortayı tepeden tabana 2’ye 1 oranında ayırır. AD 6k demiştik. AG 4k ve GD 2k olur. Bu sebeple NG AG AN 4k 3k k dır. O halde; AD GD 6k 2k 8k 8 b AD NG 6k k 7k 7 uluruz. 22
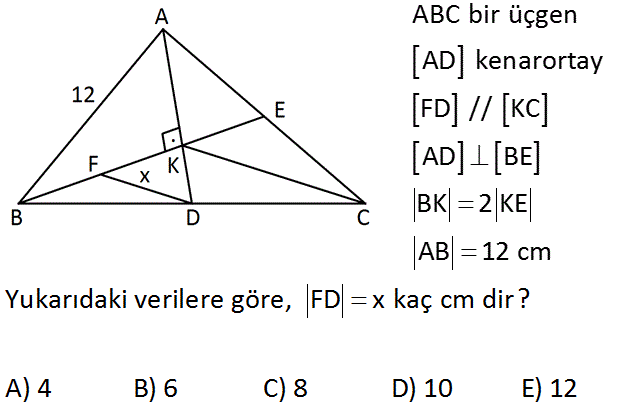
www.matematikkolay.net ABC bir üçgen AD kenarortay FD // KC AD BE BK 2 KE AB 12 cm Yukarıdaki verilere göre, FD x kaç cm dir? A) 4 B) 6 C) 8 D) 10 E) 12 : Çözüm AD kenarortay ve BE doğrusu K noktasında 1’e 2 oranında parçalandığı için K noktası ağırlık merkezidir. CK doğrusunu devam ettirirsek, bu doğru da kenarortay olur. K açısı 90 olduğundan burada muhteş em üçlü oluşur. Her biri 6 cm olur. KC 2.6 12 cm olur. AD kenarortayından dolayı BD DC dir. FD / /KC olduğundan FD uzunluğu KC’nin yarısıdır. Orta taban 12 FD 6 cm buluruz. 2 www.matematikkolay.net 25
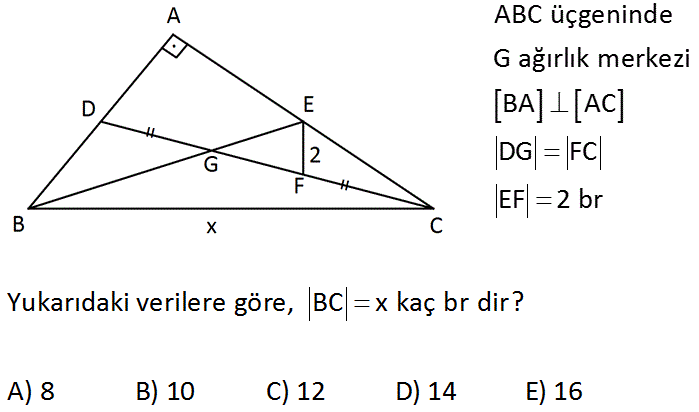
ABC üçgeninde G ağırlık merkezi BA AC DG FC EF 2 br Yukarıdaki verilere göre, BC x kaç br dir? A) 8 B) 10 C) 12 D) 14 E) 16 www.matematikkolay.net : Çözüm Ağırlık merkezi, bir kenarortayı köşeden kenara 2’ye 1 oranında böler. DG a ise GC 2a dır. FC a verilmiş. GF 2a a a kalır. E noktası AC nin orta noktasıdır. BE kenarortay old. AGC üçgenide EF uzun luğu orta tabandır. E ve F orta noktalar olduğu için EF 2 cm ise AG 2 EF 2.2 4 cm olur. AG 4 olduğundan GT 2 olur. 2’ye 1 orandan dolayı AT 6 ise BT CT 6 cm dir. Muhteş. üçlü x 6 6 12 br buluru z. 30

