Soru Sor sayfası kullanılarak Üçgende Kenarortay konusu altında Ağırlık Merkezi, Kenarortayların kesim noktası ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU
3.SORU
4.SORU
5.SORU
6.SORU

7.SORU
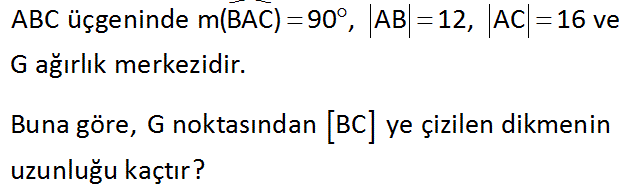

8.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
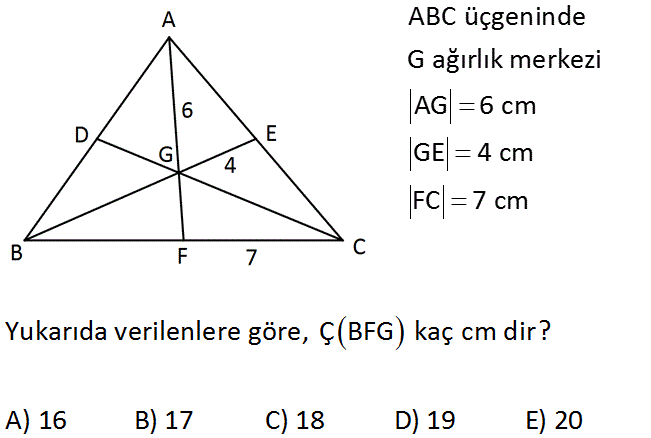
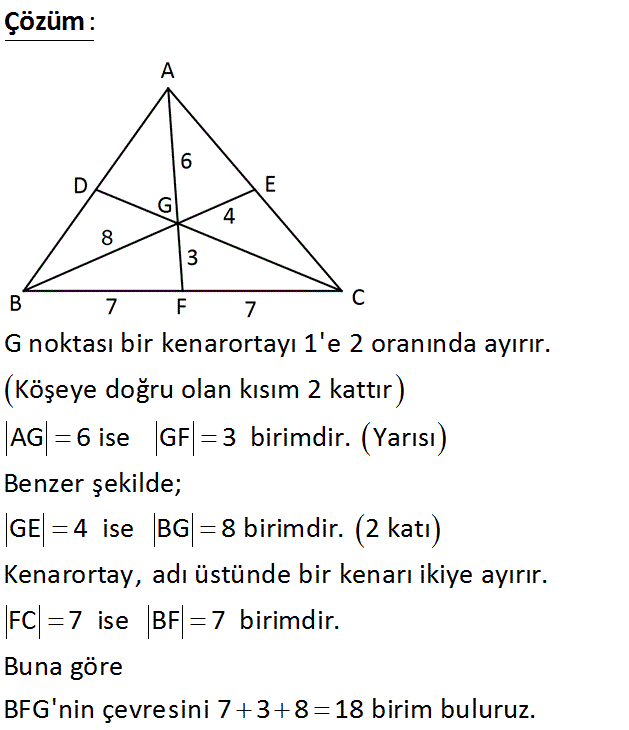
ABC üçgeninde G ağırlık merkezi AG 6 cm GE 4 cm FC 7 cm Yukarıda verilenlere göre, ÇBFG kaç cm dir? A) 16 B) 17 C) 18 D) 19 E) 20 Çözüm: www.matematikkolay.net G noktası bir kenarortayı 1’e 2 oranında ayırır. Köşeye doğru olan kısım 2 kattır AG 6 ise GF 3 birimdir. Yarısı Benzer şekilde; GE 4 ise BG 8 birimdir. 2 katı Kenarortay, adı üstünde bir kenarı ikiye ayırır. FC 7 ise BF 7 birimdir. Buna göre BFG’nin çevresini 7 3 8 18 birim buluruz. 16
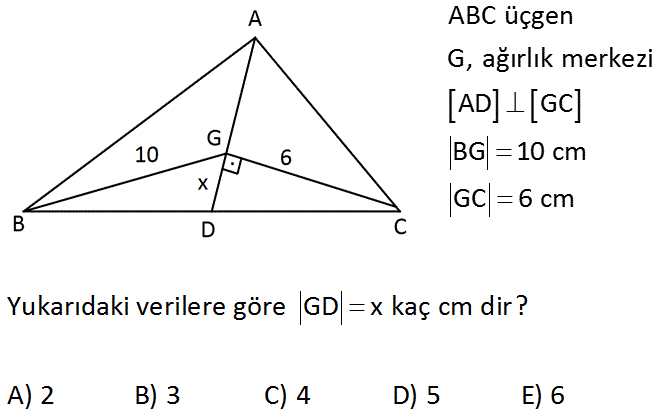
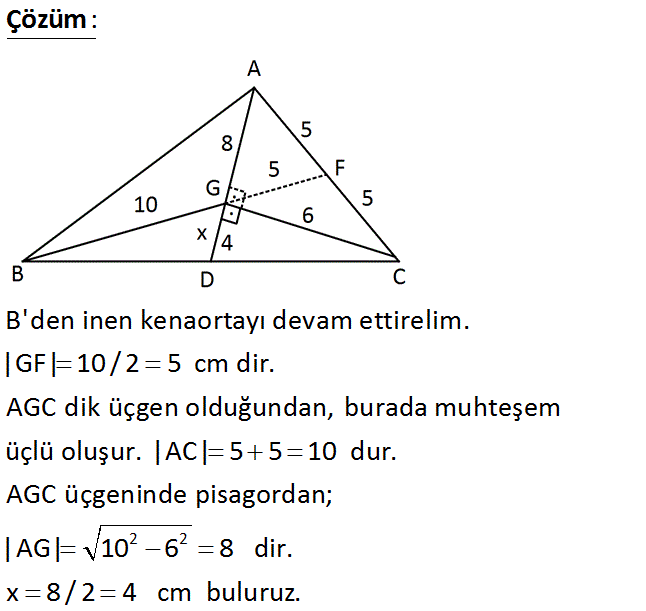
ABC üçgen G, ağırlık merkezi AD GC BG 10 cm GC 6 cm Yukarıdaki verilere göre GD x kaç cm dir? A) 2 B) 3 C) 4 D) 5 E) 6 Çözüm: www.matematikkolay.net 2 2 B’den inen kenaortayı devam ettirelim. |GF| 10 / 2 5 cm dir. AGC dik üçgen olduğundan, burada muhteşem üçlü oluşur. |AC| 5 5 10 dur. AGC üçgeninde pisagordan; |AG| 10 6 8 dir. x 8 / 2 4 cm buluruz. 5
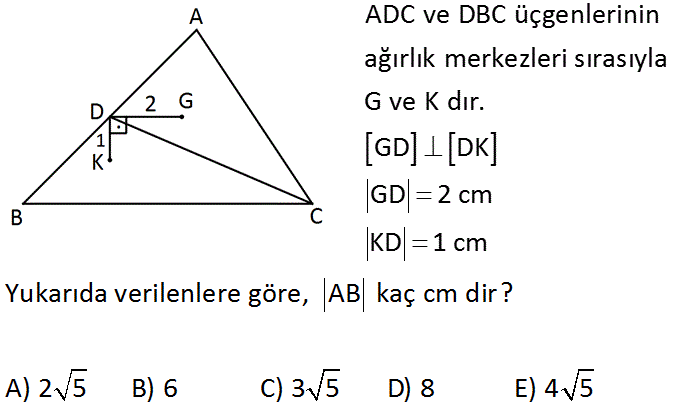
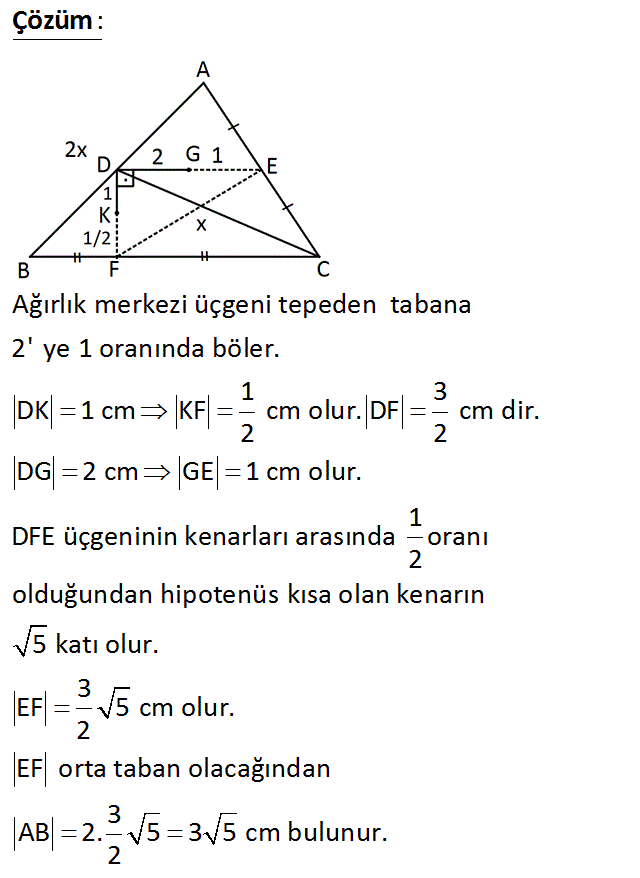
ADC ve DBC üçgenlerinin ağırlık merkezleri sırasıyla G ve K dır. GD DK GD 2 cm KD 1 cm Yukarıda verilenlere göre, AB kaç cm dir? A) 2 5 B) 6 C) 3 5 D) 8 E) 4 5 Çözüm: www.matematikkolay.net Ağırlık merkezi üçgeni tepeden tabana 2′ ye 1 oranında böler. 1 3 DK 1 cm KF cm olur. DF cm dir. 2 2 DG 2 cm GE 1 cm olur. 1 DFE üçgeninin kenarları arasında oranı 2 olduğundan hipotenüs kısa olan kenarın 5 katı olur. 3 EF 5 cm olur. 2 EF orta taban olacağından 3 AB 2. 5 3 5 cm bulunur. 2 12
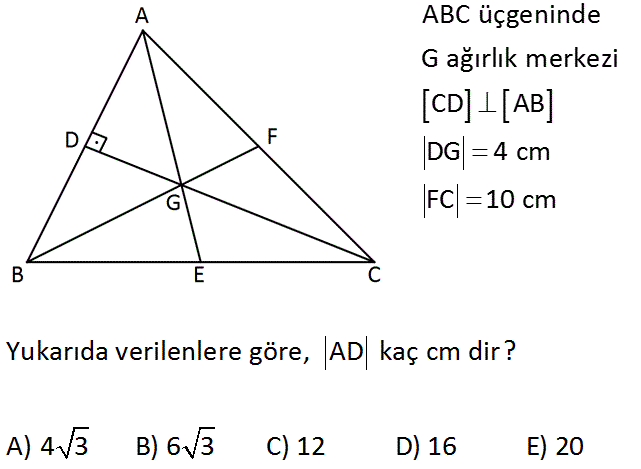
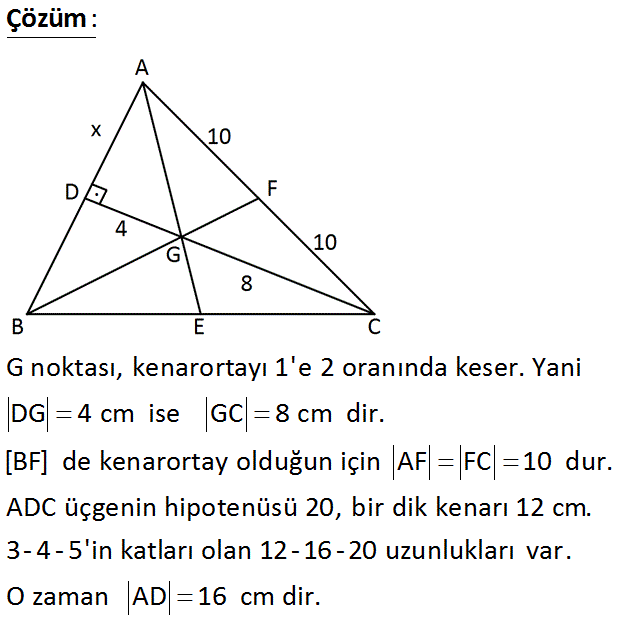
ABC üçgeninde G ağırlık merkezi CD AB DG 4 cm FC 10 cm Yukarıda verilenlere göre, AD kaç cm dir? A) 4 3 B) 6 3 C) 12 D) 16 E) 20 Çözüm: www.matematikkolay.net G noktası, kenarortayı 1’e 2 oranında keser. Yani DG 4 cm ise GC 8 cm dir. [BF] de kenarortay olduğun için AF FC 10 dur. ADC üçgenin hipotenüsü 20, bir dik kenarı 12 cm. 3- 4 – 5’in katları olan 12 – 16 – 20 uzunlukları var. O zaman AD 16 cm dir. 13
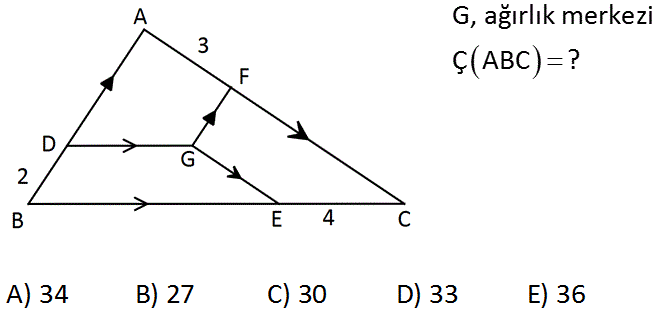
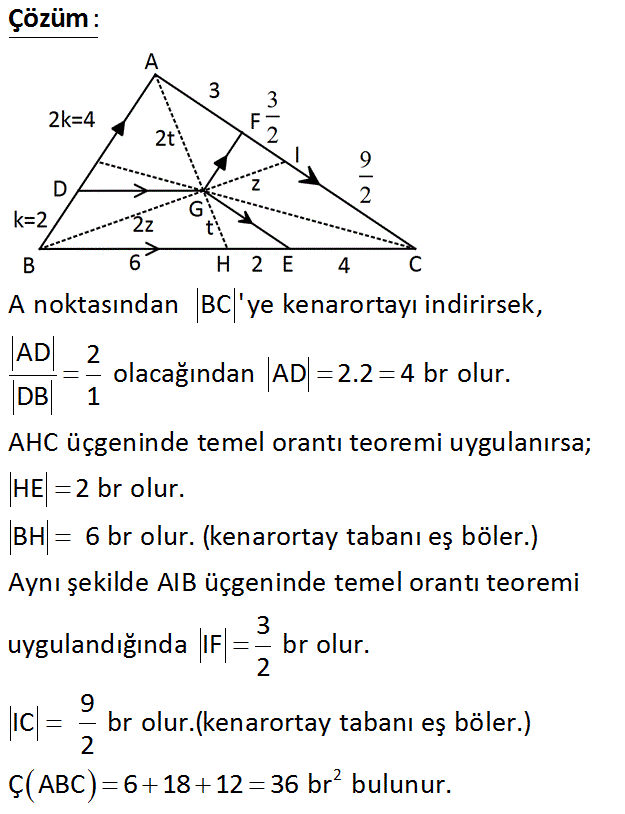
G, ağırlık merkezi Ç ABC ? A) 34 B) 27 C) 30 D) 33 E) 36 : Çözüm www.matematikkolay.net A noktasından BC ‘ ye kenarortayı indirirsek, AD 2 olacağından AD 2.2 4 br olur. DB 1 AHC üçgeninde temel orantı teoremi uygulanırsa; HE 2 br olur. BH 6 br olur. (kenarortay tabanı eş böler.) Aynı şekilde AI 2 B üçgeninde temel orantı teoremi 3 uygulandığında IF br olur. 2 9 IC br olur.(kenarortay tabanı eş böler.) 2 Ç ABC 6 18 12 36 br bulunur. 10
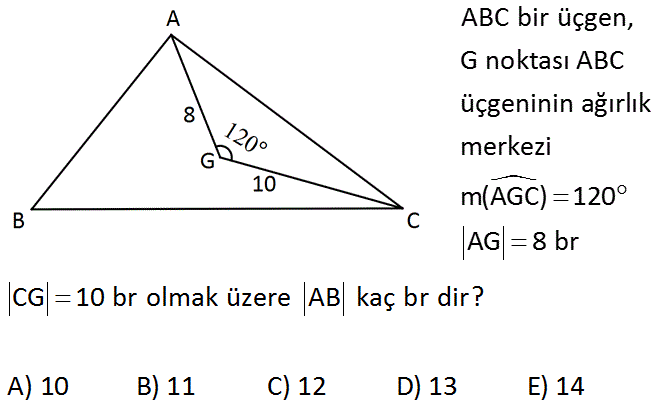
ABC bir üçgen, G no ktası ABC üçgeninin ağırlık merkezi m(AGC) 120 AG 8 br CG 10 br olmak üzere AB kaç br dir? A) 10 B) 11 C) 12 D) 13 E) 14 : Çözüm 2 2 2 2 2 2 Ağırlık merkezi kenarortayı 2′ ye 1 oranında ayırır. Buradan |DG|’ yi 5 buluruz. |AD| uzunluğunu ise kosinüs teoremi ile bulabiliriz. |AD| 5 8 2.5.8.cos60 1 |AD| 25 64 2.5.8 2 |AD| 89 40 |AD| 49 |AD| 7 b uluruz. |AB| 2.7 14 buluruz. 2
ABC üçgeninde m(BAC) 90 , AB 12, AC 16 ve G ağırlık merkezidir. Buna göre, G noktasından BC ye çizilen dikmenin uzunluğu kaçtır? Çözüm: www.matematikkolay.net Verilen üçgeni çizdiğimizde hipotenüs 20 br olur. Ağırlık merkezi kenar ortayı 2’ye 1 oranında böler. Üçgenin yüksekliğini çizdiğimizde; h.20=12.16 12.16 48 h= br. 20 5 G den inen yükseklik h’ın 3’te 1’i kad ardır. h 48 16 3,2 br bulunur. 3 3.5 5 9
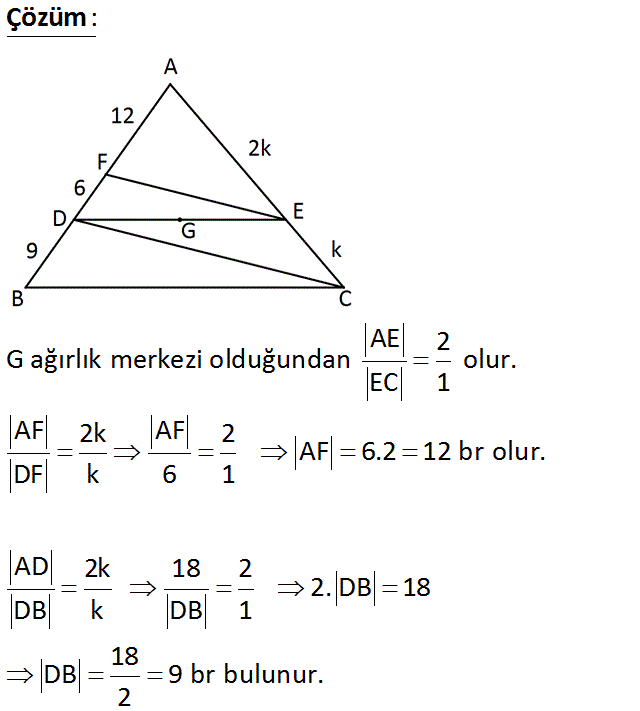
ABC üçgeninde G ağırlık merkezi DE // BC FE // DC DF 6 br Yukarıda verilenlere göre, DB kaç br dir? A) 4 B) 6 C) 8 D) 9 E) 12 Çözüm: www.matematikkolay.net AE 2 G ağırlık merkezi olduğundan olur. EC 1 AF 2k AF 2 AF 6.2 12 br olur. DF k 6 1 AD 2k 18 2 2. DB 18 DB k DB 1 18 DB 9 br bulunur. 2 11

