Soru Sor sayfası kullanılarak Üçgende Alan konusu altında Üçgende Alan Zor Sorular ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU

3.SORU


4.SORU


5.SORU
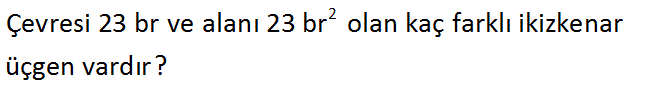
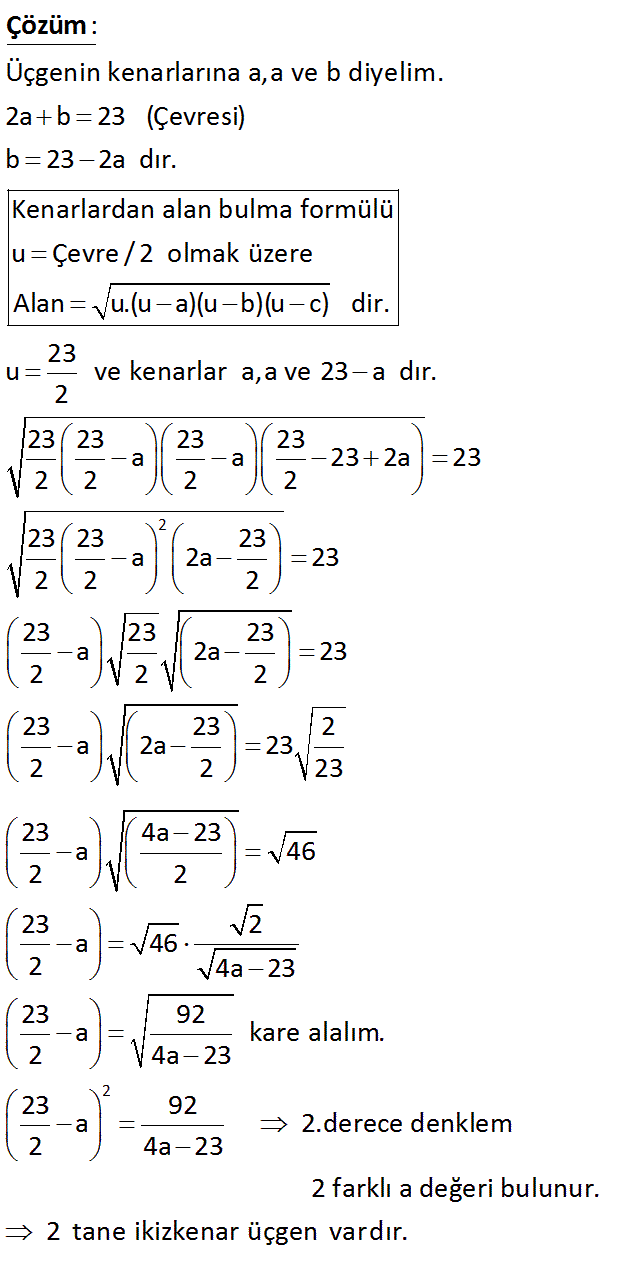
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
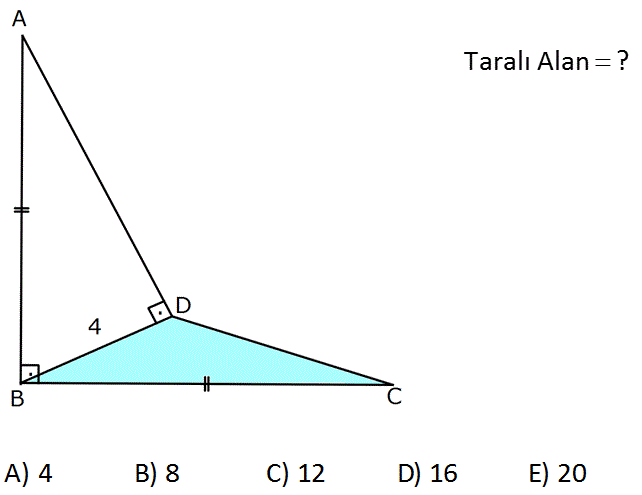
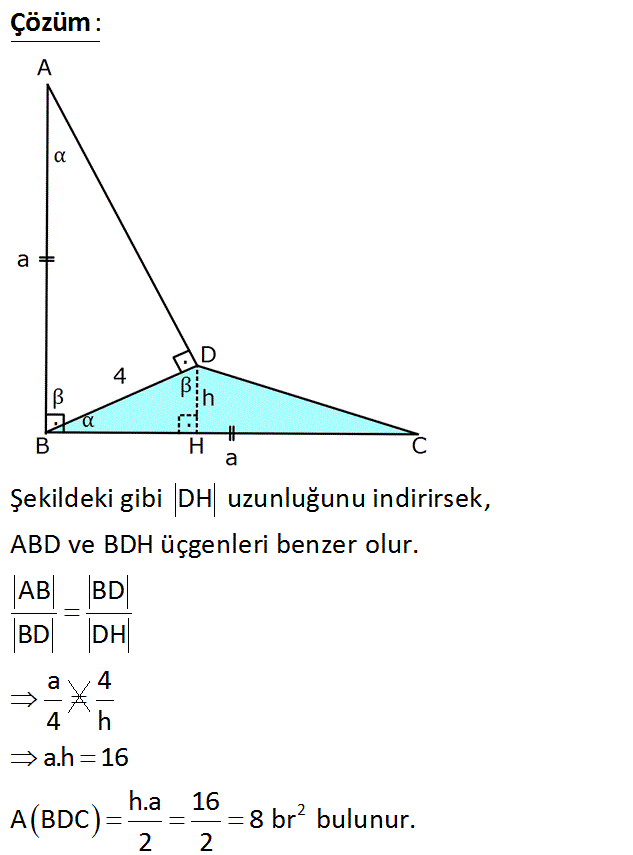
www.matematikkolay.net Taralı Alan ? A) 4 B) 8 C) 12 D) 16 E) 20 : Çözüm Şekildeki gibi DH uzunluğunu indirirsek, ABD ve BDH üçgenleri benzer olur. AB BD BD DH a 4 2 4 h a.h 16 h.a 16 A BDC 8 br bulunur. 2 2 www.matematikkolay.net 17
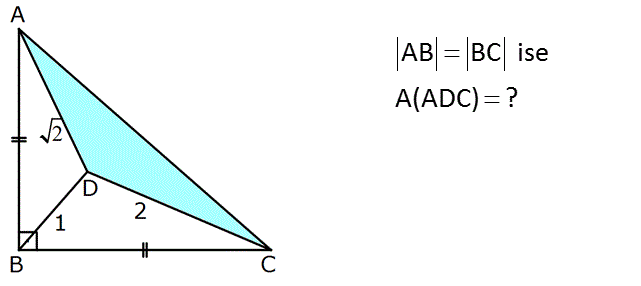
AB BC ise A(ADC) ? www.matematikkolay.net : ÇözümABD üçgeninin eşini BEC olarak çizelim. m(ABD) a , m(BAD) b olsun. m(EBC) a, m(BCE) b , BE 1 , EC 2 olur. BDE üçgeninin kenarları 1’er birim ve aradaki açı da 90 olduğundan DE 2 dir. 45 45 90 DEC 2 üçgeninde de kenarlar 2 2 2 birim ise bu üçgen de bir 45- 45-90 üçgenidir. m(DEC) 90 dir. Taralı alanın tabanını AD 2 kabul edersek, buna ait yükseklik EC 2 dir. 2 2 O halde Alan 1 br buluruz. 2 35
a b c a b c a, b ve c bir üçgenin kenar uzunluklarını; h , h ve h de kenarlara ait yükseklikleri göstermektedir. a b 9 1 1 1 h h h olduğuna göre, c kaçtır? A) 2 B) 3 C) 4 D) 6 E) 9 a a b c Bir üçgenin kenarı ile o kenara ait yükseklik çarpılıp, yarıya bölünürse o üçgenin alanı bulunur. a.h Örneğin; A dır. 2 a.h 2A diyebiliriz. Aynı şekilde; b.h 2A ve c.h 2A dır. : Buna göre Çözüm a b c a b c a b c ; 1 1 1 a b c h h h a.h b.h c.h a b c 2A 2A 2A a b 2A c 2A a b c 9 c buluruz. 46
a b 2 2 2 2 a b ABC üçgeninin iki kenarının uzunlukları a ve b; bu kenarlara ait yükseklik uzunlukları sırasıyla h ve h dir. a h b h olduğuna göre, m(ACB) kaç derecedir? www.matematikkolay.net 2 2 2 2 a b 2 2 2 2 b a a a b b 2 2 2 2 b a 2 2 a 2 2 b a b 2 2 2 a 2 2 2 b a b 2 2 2 2 b a 2 2 2 b a b 2 2 2 2 2 2 2 b a b b a 2 2 2 b a a h b h a b h h ah Not : a.h b.h b h a b h h ah a h h h : a h a h h h a h a h h h h a h a h h (h h ) a (h h ) Çözüm 2 2 2 b b a h (h h ) 2 2 b b a h a h a kenarı , b’nin yüksekliği ise bu bir dik üçgen olmalıdır. m(ACB) 90 buluruz. 11
2 Çevresi 23 br ve alanı 23 br olan kaç farklı ikizkenar üçgen vardır? www.matematikkolay.net Üçgenin kenarlarına a,a ve b diyelim. 2a b 23 (Çevresi) b 23 2a dır. Kenarlardan alan bulma formülü u Çevre / 2 olmak üzere Alan u.(u a)(u b)(u c) dir. 23 u ve kenarlar a,a ve 23 a dır. 2 23 2 2 2 : 3 Çözüm 2 23 23 a a 23 2a 23 2 2 23 23 23 a 2a 23 2 2 2 23 23 23 a 2a 23 2 2 2 23 23 2 a 2a 23 2 2 23 23 4a 23 a 46 2 2 23 2 a 46 2 4a 23 23 92 a kare 2 4a 23 2 alalım. 23 92 a 2.derece denklem 2 4a 23 2 farklı a değeri bulunur. 2 tane ikizkenar üçgen vardır. www.matematikkolay.net 28


hocam 3. soru yanlis bir soru
Uyarınız için teşekkürler. Üçgen eşitsizliğini sağlamayan değerlerle soru oluşturulmuş. Şimdi düzeltildi.