Alan parçalama, Alanların Oranı

www.matematikkolay.net ABC üçgen 2 BD 2 DE 7 AE 6 EC Yukarıdaki verilere göre, taralı alanın ABC üçgeninin alanına oranı kaçtır? 12 17 18 19 21 A) B) C) D) E) 23 41 65 75 89 : Çözüm Taralı alana 18A dersek, 3k 18A ise 2k 16 A olur. A ABE 18A 12A 30A olur. 6t 30 A ise 7t 35A olur. A ABC 30A 35A 65A olur. Taralı Alan 18A 18 buluruz. A ABC 65A 65       16
2 GE // BC DG // AF G, Ağırlık merkezi G BF A(BDG) 16 cm  2 Yukarıdaki verilere göre, taralı alanların toplamı kaç cm dir? A) 12 B) 14 C) 21 D) 28 E) 36 www.matematikkolay.net : Çözüm Kenarortay, ağırlık merkezi tarafından 2’ye 1 oranın – da bölünür. Bu sebeple BG 2k, GF k diyebiliriz. DG/ /AF olduğundan BDG BAF dır. BG 2k 2 Benzerlik oranı da tür. BF 3k 3 Alanları oranı da, benzerli  2 k oranının karesine eşittir. A(BDG) 2 16 A(BAF) 3        4 4 A(BAF) 2 2 A(BAF) 36 cm 9 Kenarortay sebebiyle AF FC dir. Dolayısıyla; A(BAF) A(BFC) 36 cm dir. GE / /BC olduğundan |FE| t , |EC| 2t diyebiliriz. A(FGE) A olsun. A(BGE) 2A olur. (Tabanı 2k,  yükseklikleri aynı) A(BFE) 3A oldu. A(BEC) 6A olur. (Tabanı 2t, yükseklikleri ay 2 2 nı) O halde; A 2A 6A 36 9A 36 A 4 cm Taralı alanlar A 6A 7A 7.4 28 cm buluruz.      18
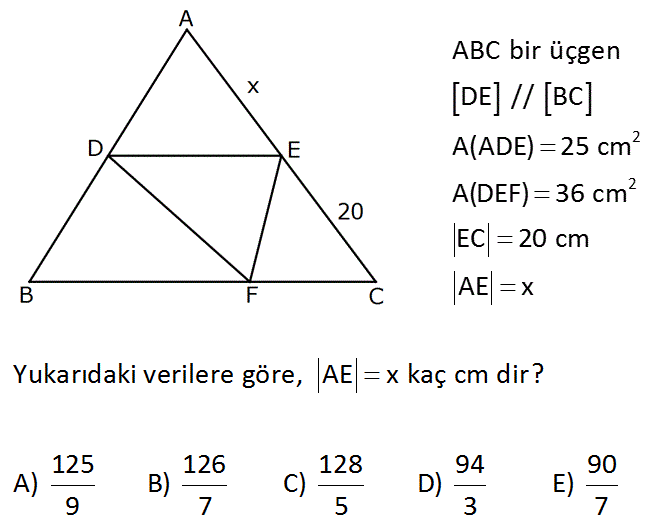
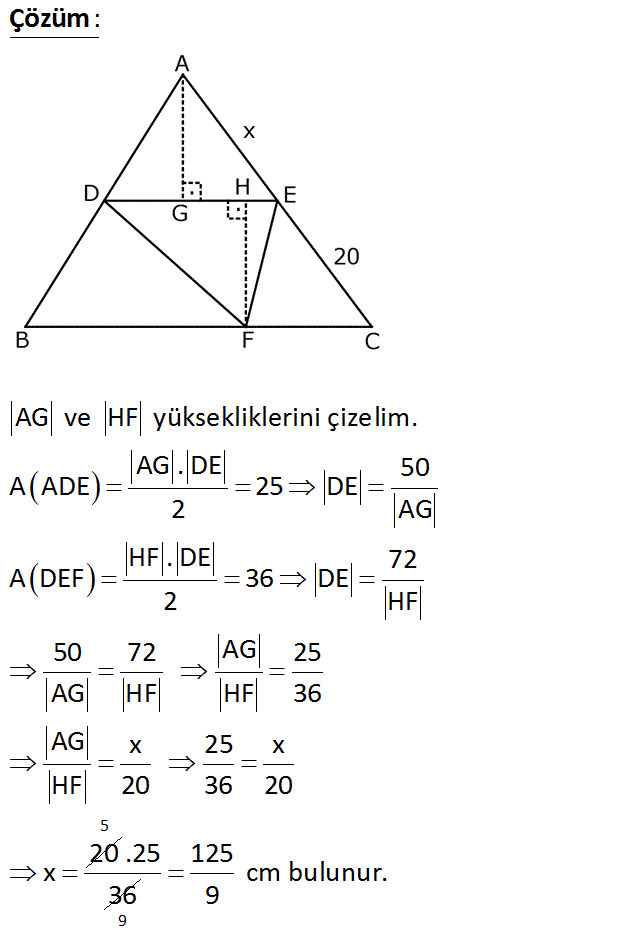
2 2 ABC bir üçgen DE // BC A(ADE) 25 cm A(DEF) 36 cm EC 20 cm AE x www.matematikkolay.net Yukarıdaki verilere göre, AE x kaç cm dir? 125 126 128 94 90 A) B) C) D) E) 9 7 5 3 7 : Çözüm AG ve HF yüksekliklerini çizelim. AG . DE 50 A ADE 25 DE 2 AG HF . DE 72 A DEF 36 DE 2 HF 50 72 AG 25 AG HF HF 36 AG x 25 x HF 20 36 20 20 x        5 .25 36 9 125 cm bulunur. 9 www.matematikkolay.net 26
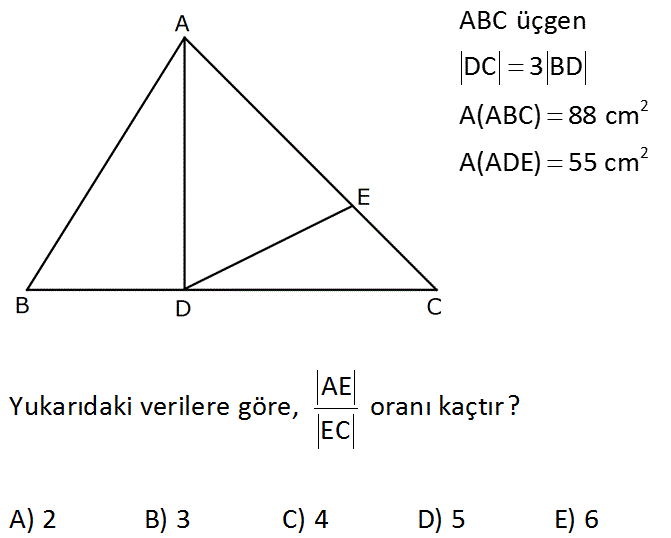
www.matematikkolay.net 2 2 ABC üçgen DC 3 BD A(ABC) 88 cm A(ADE) 55 cm AE Yukarıdaki verilere göre, oranı kaçtır? EC A) 2 B) 3 C) 4 D) 5 E) 6 : Çözüm Üçgende alan tabanlarının oranıyla parçalanır. A ABC 88 ise A ABD 22, A ADC 66 olur. A ADE 55 ise A DEC 11 olur. A ADE AE 55 5 bulunur. A DEC EC 11 41
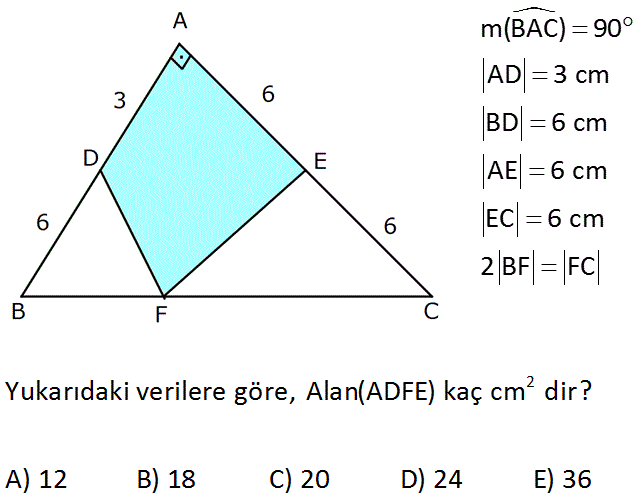
www.matematikkolay.net m(BAC) 90 AD 3 cm BD 6 cm AE 6 cm EC 6 cm 2 BF FC  2 Yukarıdaki verilere göre, Alan(ADFE) kaç cm dir? A) 12 B) 18 C) 20 D) 24 E) 36 www.matematikkolay.net : Çözüm 2 k 2k 2 2 AB . AC 9.12 A ABC 54 cm dir. 2 2 2 BF FC BF k ise BD 2k dır. ABF üçgeni ile AFC üçgeni, Tüm alanı tabanları oranında paylaşırar. 54 cm yi 1’e 2 oranında paylaştırısak; A ABF 18 cm ve  2 2 2 A AFC 36 cm olur. ADF üçgeni ile DBF üçgeni, ABF nin alanını tabanları oranında paylaşırar. 18 cm yi 3’e 6 oranında paylaştırısak; A ADF 6 cm olur. AFE üçgeni ile EFC üçgeni, AFC nin alanını 2 2 2 tabanları oranında paylaşırar. 36 cm yi 6’ya 6 oranında paylaştırısak; A AFE 18 cm olur. A ADFE A ADF A AFE 6 18 24 cm dir.   www.matematikkolay.net 53
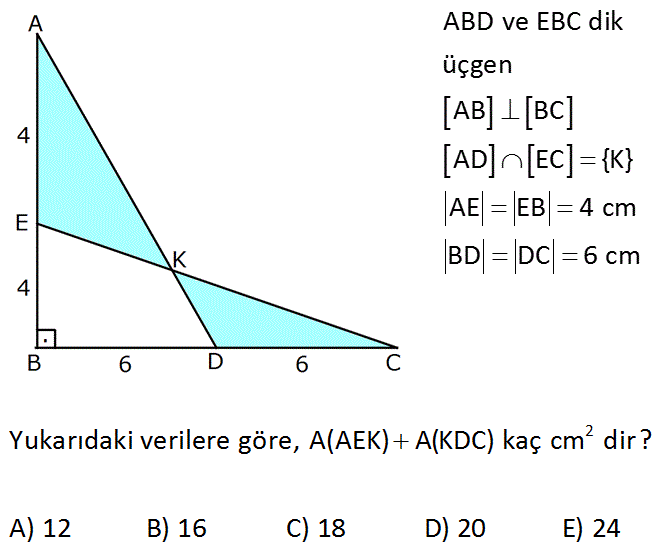
ABD ve EBC dik üçgen AB BC AD EC {K} AE EB 4 cm BD DC 6 cm  2 Yukarıdaki verilere göre, A(AEK) A(KDC) kaç cm dir? A) 12 B) 16 C) 18 D) 20 E) 24  : Çözüm www.matematikkolay.net [AD] ve [EC] kenarortay olduğundan, bunların kesişim noktasından geçen [BT] doğrusu da kenarortaydır. Tüm kenarortaylar, üçgenin alanını 6 eş parçaya bölerler. Bu sebeple 6A Üçgenin Alanı 8 6A 4 .12 2 2 2 6A 48 A 8 cm dir. Taralı alanlar A A 2A 2.8 16 cm buluruz.    54
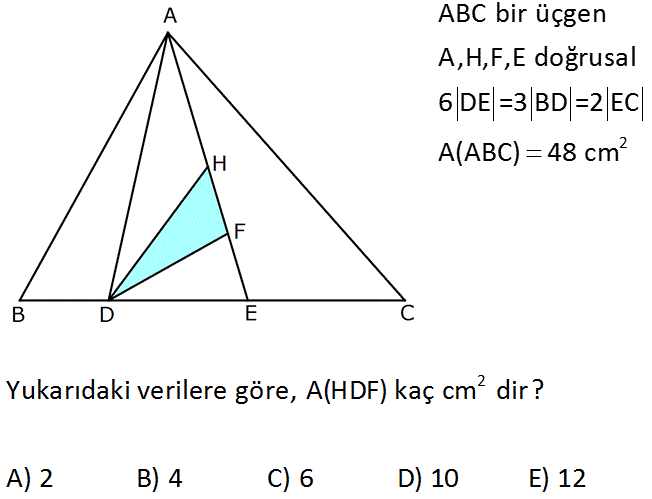
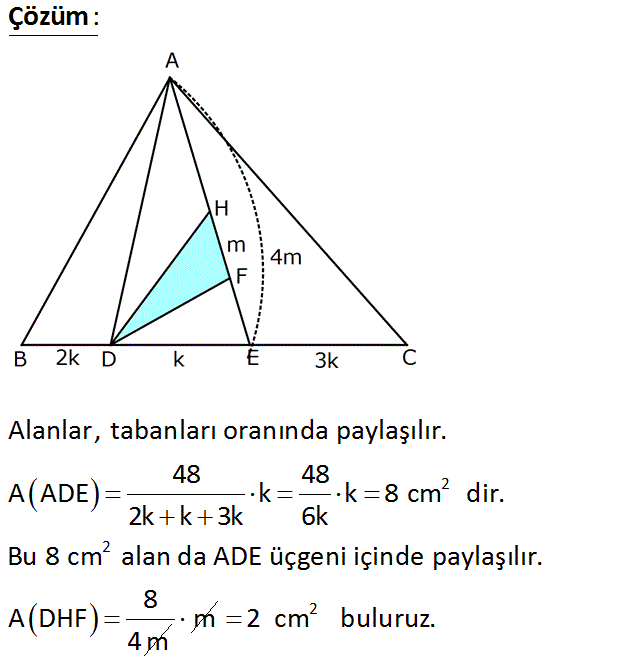
2 ABC bir üçgen A,H,F,E doğrusal 6 DE =3 BD =2 EC A(ABC) 48 cm 2 Yukarıdaki verilere göre, A(HDF) kaç cm dir? A) 2 B) 4 C) 6 D) 10 E) 12 www.matematikkolay.net : Çözüm 2 2 Alanlar, tabanları oranında paylaşılır. 48 48 A ADE k k 8 cm dir. 2k k 3k 6k Bu 8 cm alan da ADE üçgeni içinde paylaşılır. 8 A DHF 4m      m 2 2 cm buluruz. 57
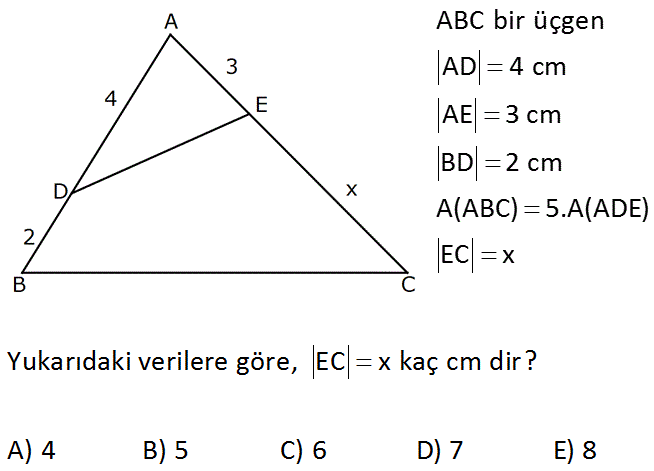
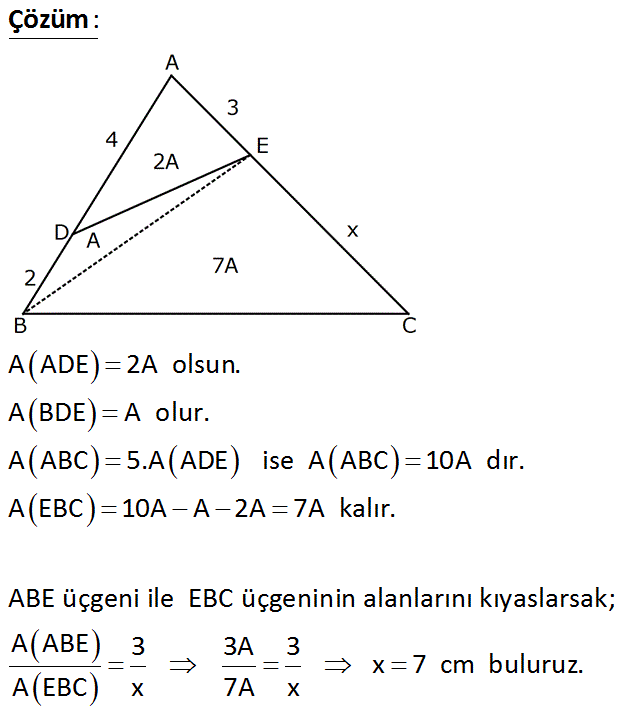
ABC bir üçgen AD 4 cm AE 3 cm BD 2 cm A(ABC) 5.A(ADE) EC x Yukarıdaki verilere göre, EC x kaç cm dir? A) 4 B) 5 C) 6 D) 7 E) 8 Çözüm: www.matematikkolay.net A ADE 2A olsun. A BDE A olur. A ABC 5.A ADE ise A ABC 10A dır. A EBC 10A A 2A 7A kalır. ABE üçgeni ile EBC üçgeninin alanlarını kıyaslarsak; A ABE 3 3A 3 x 7 cm buluruz. A EBC x 7A x     58
ABC eşkenar üçgenin iç teğet çemberi ile DEFG karesi çizilmiştir. Yukarıdaki verilere göre, karenin alanının eşkenar üçgeninin alanına oranı kaçtır? 3 2 2 2 3 A) B) C) 2 3 9 5 2 D) E) 2  3 5 Çözüm: www.matematikkolay.net Çemberin yarıçapına 1 diyelim. Karenin bir kenarı 2 birim olur. (45 – 45 -90) 30 -60 -90 üçgeni nedeniyle |AZ| 2 birim olur. Üçgenin yüksekliği 2 1 3 birimdir. ADC (30 -60 -90) üçgenine göre üçgenin bir kenarı 2  2 2 3 birimdir. 2 2 8 Alanları oranı 2 3 3 12 3 4 4 2 12 3 -3 3 2 2 3 buluruz. 3 3 9 25
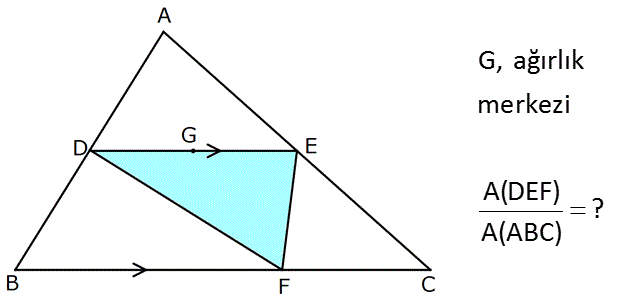
G, ağırlık merkezi A(DEF) ? A(ABC) Çözüm: www.matematikkolay.net Ağırlık merkezi kenarortayı, köşeden kenara 2’ye 1 oranında ayırır. Yükseklikler ve tabanların oranı da buna uygun olacaktır. 2a.h A DEF 2 2 buluruz. A ABC 3a.3h 9 2 59
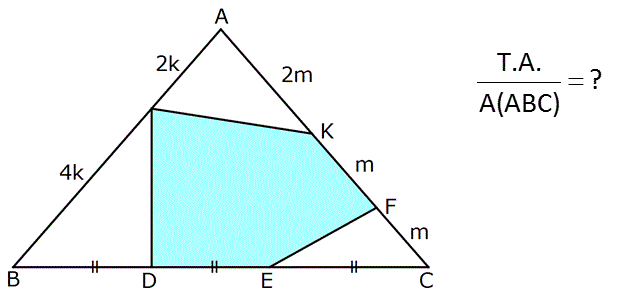
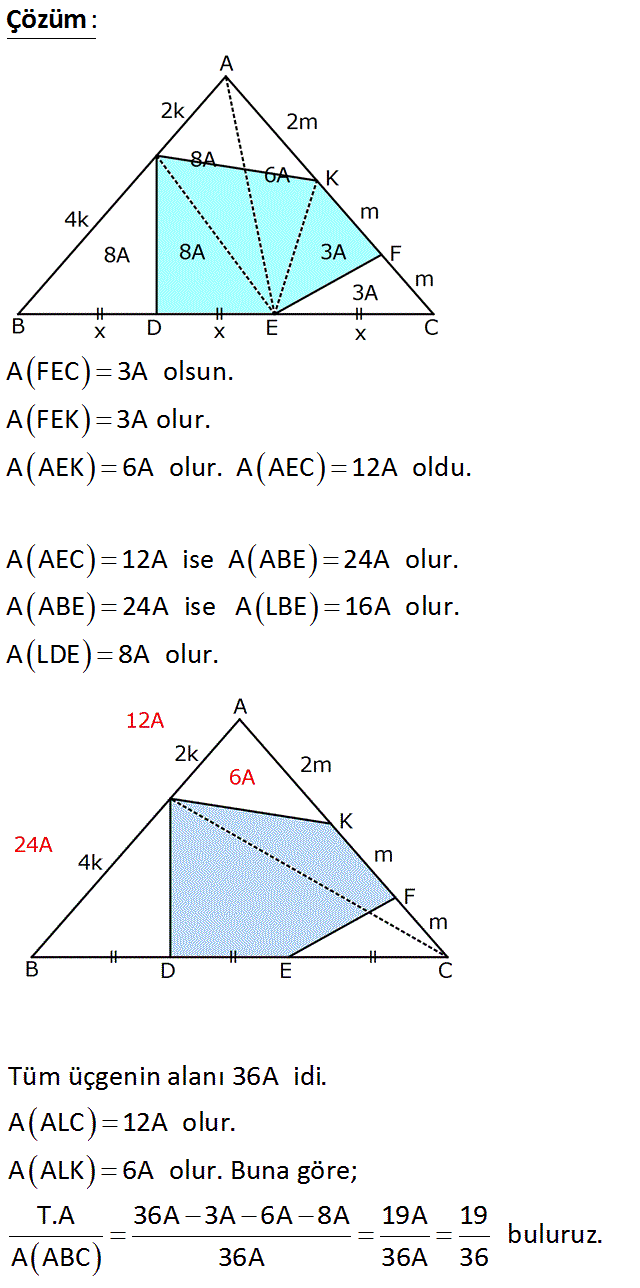
T.A. ? A(ABC) www.matematikkolay.net : Çözüm A FEC 3A olsun. A FEK 3A olur. A AEK 6A olur. A AEC 12A oldu. A AEC 12A ise A ABE 24A olur. A ABE 24A ise A LBE 16A olur. A LDE 8A olur. Tüm üçgenin alanı 36A idi. A ALC 12A olur. A ALK 6A olur. Buna göre; T.A 36A 3A 6A 8A 19A 19 buluruz. A ABC 36A 36A 36    www.matematikkolay.net 61