Soru Sor sayfası kullanılarak Üçgende Açıortay konusu altında İç teğet çemberinin merkezi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
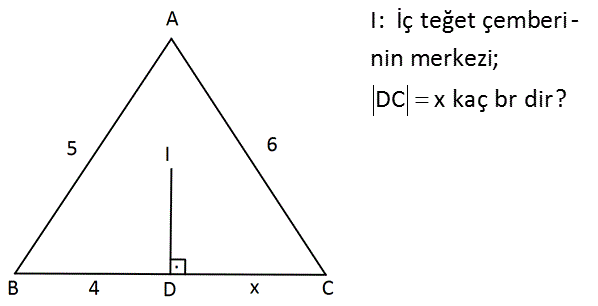

2.SORU


3.SORU
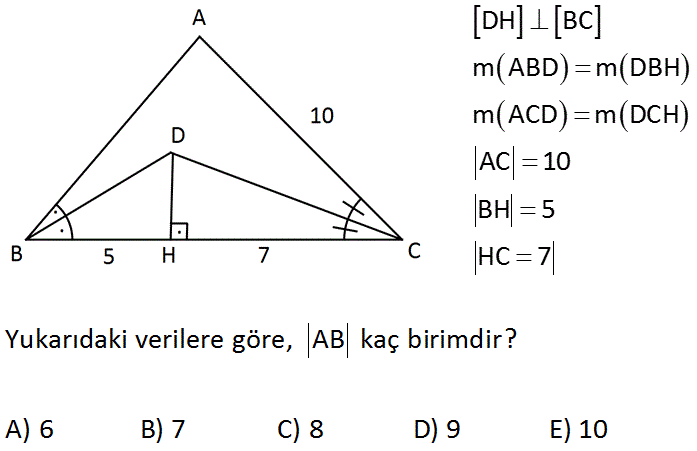
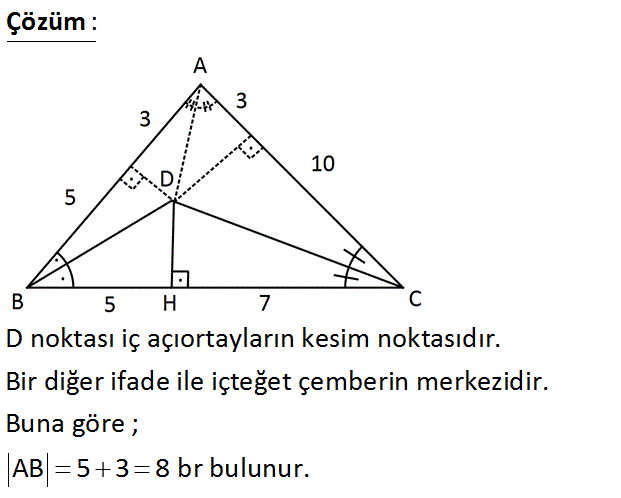
4.SORU


5.SORU
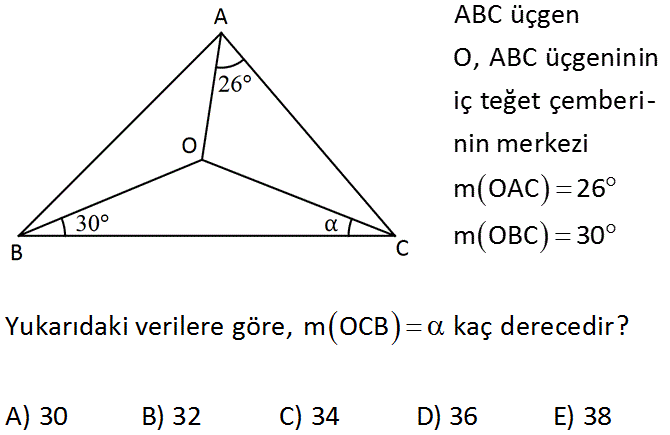
6.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
I: İç teğet çemberi – nin merkezi; DC x kaç br dir? Çözüm: İçteğet çemberinin merkezi, açıortayların kesişim yeridir. Açıortayların kolları birbirine eşittir. Buradan adım adım giderek x=5 buluruz. 14
ABC üçgen, D: iç teğet çemberinin merkezi, EF // BC BC 12 cm BE 3 cm CF 5 cm Yukarıdaki verilere göre, ÇAEF kaç cm dir? A) 16 B) 18 C) 20 D) 22 E) 24 Çözüm: İç teğet çemberinin merkezi, açıortayların kesişim yeridir. Şekildeki gibi iki açıortayı çizdiğimizde, iç ters açılardan; EBD üçgeni ve DFC üçgeninin ikizkenar üçgen olduklarını göreceğiz. Buna göre |EF| 3 5 8 dir. ABC ile AEF üçgenleri arasında benzerlikten; |AE| 6 ve |AF| 10 cm bulunur. Çevre(AEF) 6 8 10 24 cm buluruz. 17
DH BC m ABD m DBH m ACD m DCH AC 10 BH 5 HC 7 Yukarıdaki verilere göre, AB kaç birimdir? A) 6 B) 7 C) 8 D) 9 E) 10 : Çözüm D noktası iç açıortayların kesim nokta sıdır. Bir diğer ifade ile içteğet çemberin merkezidir. Buna göre ; AB 53 8 br bulunur. 22
Dik koordinat düzleminde, köşeleri A 12, 6 , B 12, 6 ve C noktaları olan ABC üçgeninin açıortay – ları orjinde kesişmektedir. Buna göre, C noktasının koordinatları toplamı kaçtır? A) 8 B) 9 C) 10 D) 11 E) 1 2 Çözüm: Açıortayların kesişim yeri içteğet çemberinin merke – zidir. Şekildeki gibi kenar uzunluklarını yazdık tan sonra; AEC ODC üçgeni arasında benzerlik uygulayabiliriz. 12 2 6 1 6 y 12 a 6 y 2a y 2a 6 dır. a y 12 a 2y (y 2a 6 yazarsak) 12 a 4a 12 24 3a a 8 dir. y 2a 6 10 buluruz. y değe ri 10 ise; C noktasının koordinatları (10,0) dır. 24
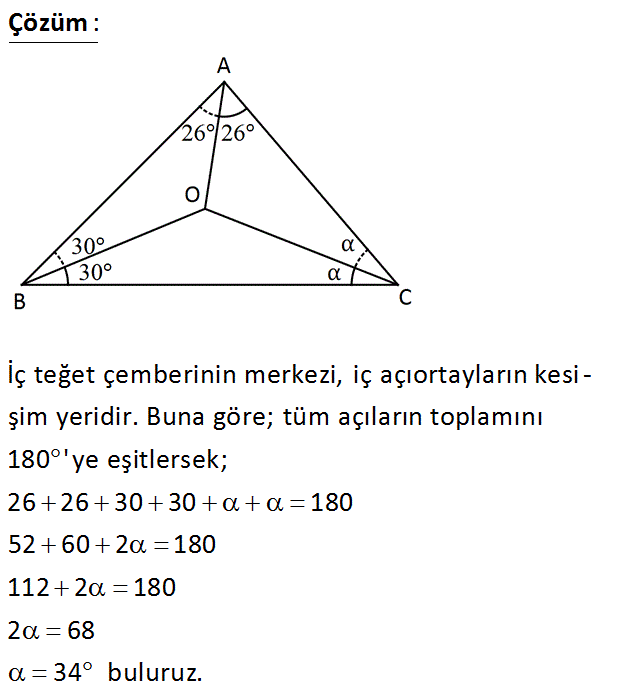
ABC üçgen O, ABC üçgeninin iç teğet çemberi – nin merkezi m OAC 26 m OBC 30 Yukarıdaki verilere göre, mOCB kaç derecedir? A) 30 B) 32 C) 34 D) 36 E) 38 : Çözüm İç teğet çemberinin merkezi, iç açıortayların kesi – şim yeridir. Buna göre; tüm açıların toplamını 180 ‘ye eşitlersek; 26 26 30 30 180 52 60 2 180 112 2 180 2 68 34 buluruz. 26
ABC üçgen AC BC BC 8 cm AC 6 cm D: İç açıortayların kesim noktası Yukarıdaki verilere göre, CD x kaç cm dir? A) 2 B) 2 2 C) 3 D) 10 E) 4 06.Ağu A(ABC) 24 tür. 2 ABC bir 6 8 10 üçgenidir. |AB| 10 6 8 10 24 Çevrenin yarısı u 12 dir. 2 2 u.r 24 olmalıdır. 12.r 24 r 2 dir. Açıortayların kesişim yeri iç teğet çemberinin merkezidir v : e Çözüm bu çemberin yarıçapını biz 2 cm bulduk. İçteğet çemberinin yarıçapı ile oluşan üçgende x uzunluğu hipotenüstür. Buradan x 2 2 buluruz 29

