Soru Sor sayfası kullanılarak Üçgende Açıortay konusu altında İç açıortayların kesim noktası ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
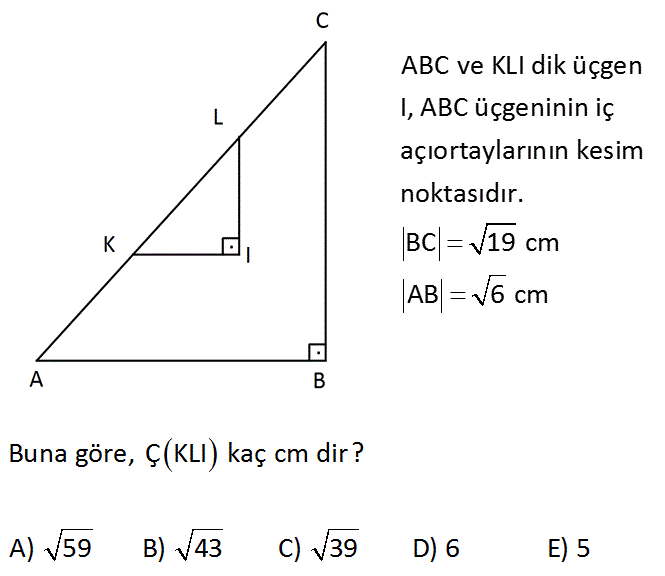

2.SORU

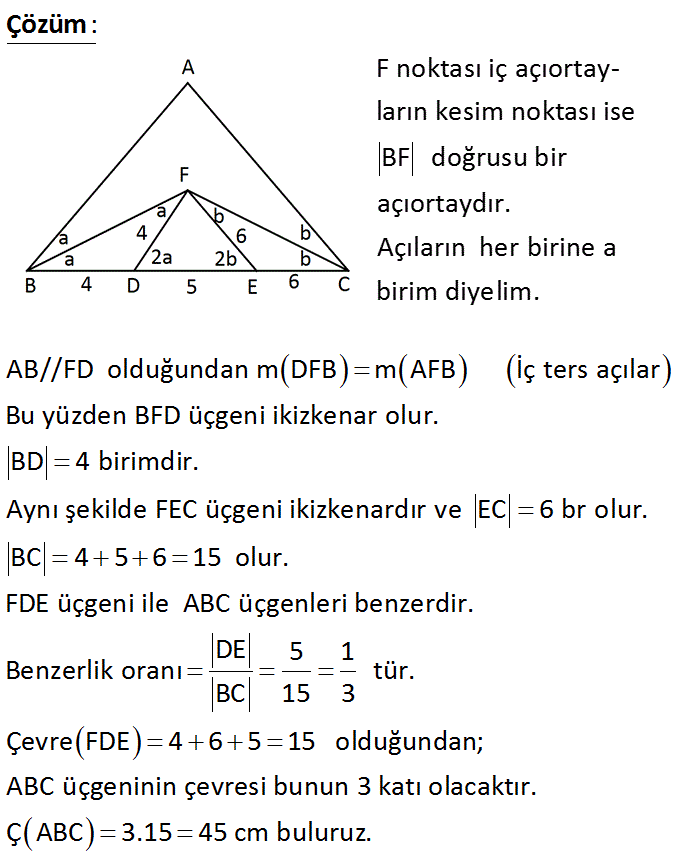
3.SORU

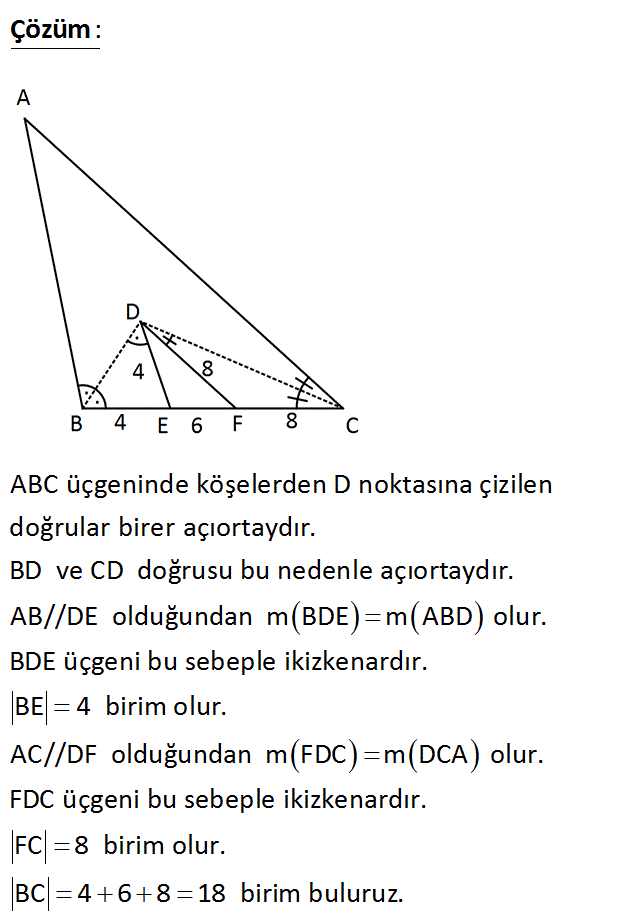
4.SORU
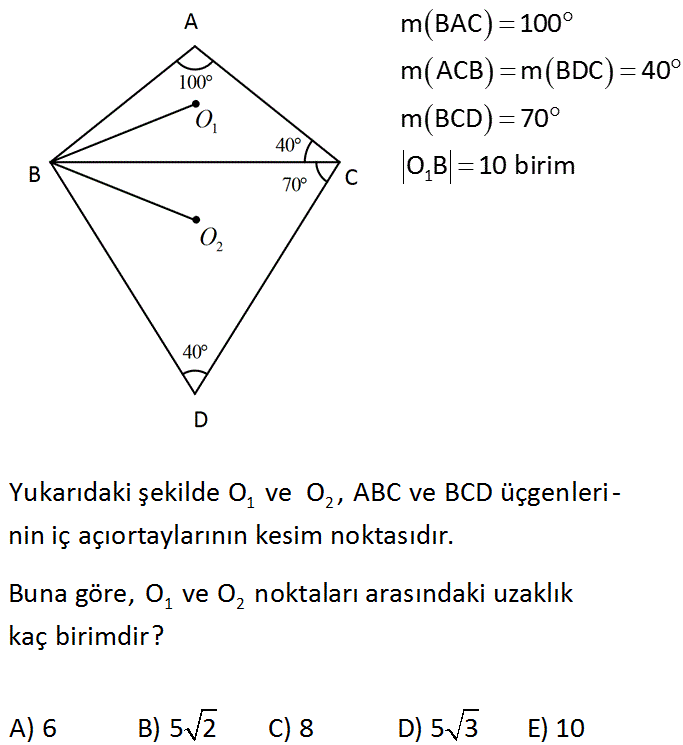
5.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
ABC ve KLI dik üçgen I, ABC üçgeninin iç açıortaylarının kesim noktasıdır. BC 19 cm AB 6 cm Buna göre, ÇKLI kaç cm dir? A) 59 B) 43 C) 39 D) 6 E) 5 Çözüm: İki üçgen de dik üçgen olduğundan; KI//AB ve LI//BC dir. AI açıortayının ayırdığı açılara a diyelim. m KIA a olur. İç ters açılar AKI üçgeni ikizkenar bir üçgen olur. KI KA x olur. 2 2 Aynı durum diğer açıortay için de geçerli. LI y olur. Çevre KLI x y z AC dir. AC 19 6 Pisagor AC 25 AC 5 buluruz. 8
ABC üçgen F: iç açıortayların kesim noktası DF // AB EF // AC DF 4 cm EF 6 cm DE 5 cm Yukarıda verilenlere göre, ÇABC kaç cm dir? A) 45 B) 36 C) 30 D) 24 E) 21 Çözüm: F noktası iç açıortayların kesim noktası ise BF doğrusu bir açıortaydır. Açıların her birine a birim diyelim. AB//FD olduğundan mDFB mAFB İç ters açılar Bu yüzden BFD üçgeni ikizkenar olur. BD 4 birimdir. Aynı şekilde FEC üçgeni ikizkenardır ve EC 6 br olur. BC 4 5 6 15 olur. FDE üçgeni ile ABC üçgenleri be nzerdir. DE 5 1 Benzerlik oranı tür. BC 15 3 Çevre FDE 4 6 5 15 olduğundan; ABC üçgeninin çevresi bunun 3 katı olacaktır. Ç ABC 3.15 45 cm buluruz. 11
AB // DE AC ve DF DE 4 birim DF 8 birim EF 6 birim Yukarıdaki şekilde D, ABC üçgeninin iç açıortayları – nın kesim noktası olduğuna göre, BC uzunluğu kaç birimdir? A) 16 B) 18 C) 20 D) 22 E) 24 : Çözüm ABC üçgeninde köşelerden D noktasına çizilen doğrular birer açıortaydır. BD ve CD doğrusu bu nedenle açıortaydır. AB//DE olduğundan m BDE m ABD olur. BDE üçgeni bu sebeple ikizkenardır. BE 4 birim olur. AC//DF olduğundan mFDC mDCA olur. FDC üçgeni bu sebeple ikizkenardır. FC 8 birim olur. BC 4 6 8 18 birim buluruz. 4
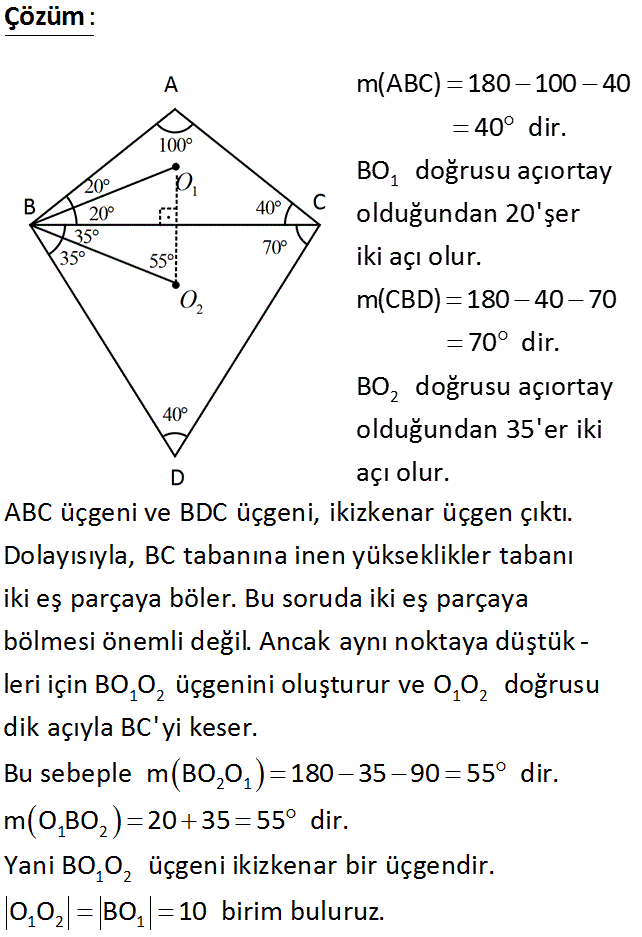
1 m BAC 100 m ACB m BDC 40 m BCD 70 O B 10 birim 1 2 1 2 Yukarıdaki şekilde O ve O , ABC ve BCD üçgenleri – nin iç açıortaylarının kesim noktasıdır. Buna göre, O ve O noktaları arasındaki uzaklık kaç birimdir? A) 6 B) 5 2 C) 8 D) 5 3 E) 10 : Çözüm 1 2 m(ABC) 180 100 40 40 dir. BO doğrusu açıortay olduğundan 20’şer iki açı olur. m(CBD) 180 40 70 70 dir. BO doğrusu açıortay olduğundan 35’er iki açı olur. ABC üçgeni ve BDC üçgeni, ikizkenar üçgen çıktı. Dolayısıyla, BC tabanına inen yükseklikler tabanı iki eş parçaya böler. Bu soruda iki eş parçaya bölmesi önemli değil. Ancak aynı noktaya düştük – leri için 1 2 1 2 2 1 1 2 1 2 1 2 1 BO O üçgenini oluşturur ve O O doğrusu dik açıyla BC’ yi keser. Bu sebeple m BO O 180 35 90 55 dir. m O BO 20 35 55 dir. Yani BO O üçgeni ikizkenar bir üçgendir. O O BO 10 birim buluruz. 2
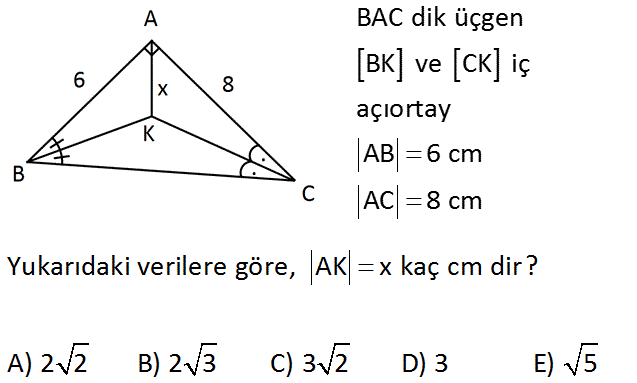
BAC dik üçgen BK ve CK iç açıortay AB 6 cm AC 8 cm Yukarıdaki verilere göre, AK x kaç cm dir? A) 2 2 B) 2 3 C) 3 2 D) 3 E) 5 Çözüm: 2 2 2 Pisagordan ; |BC| 6 8 10 dur. 6.8 48 Üçgenin alanı da 24 cm dir. 2 2 Açıortayların kesim yeri iç teğet çemberinin merke – zidir. A açısının dik olması nedeniyle bu çemberin yarıçapları ile üçgenin üst kısmında bir kare oluşur. Şimdi r yi bulalım. Üçgenin alanı u.r (u Çevrenin yarısı) 6 8 10 24 r 24 2 24 r r 2 dir. 2 O halde, x r 2 2 2 cm buluruz. 40

