Soru Sor sayfası kullanılarak Üçgende Açıortay konusu altında İç Açıortay Bağıntısı, Açıortay oranları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
2.SORU
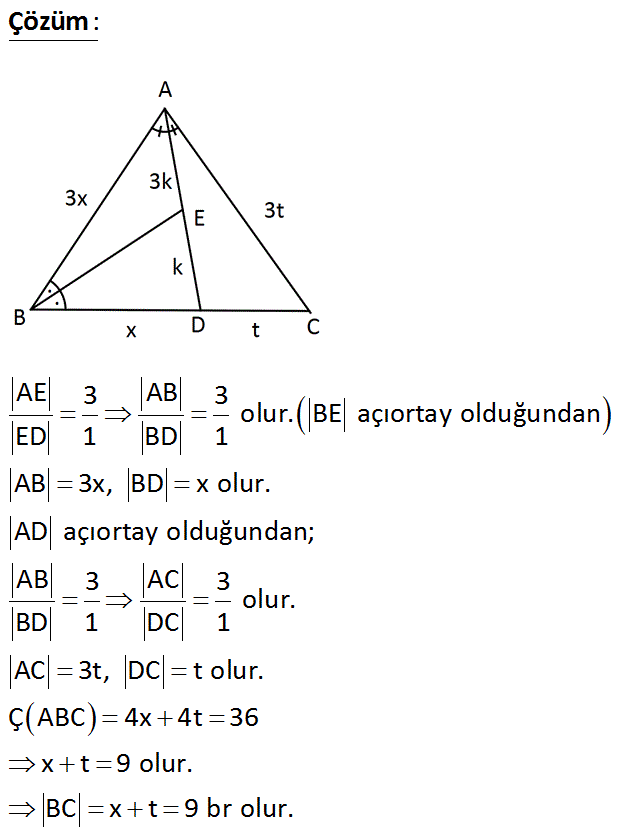
3.SORU
4.SORU
5.SORU
6.SORU
7.SORU
8.SORU
9.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
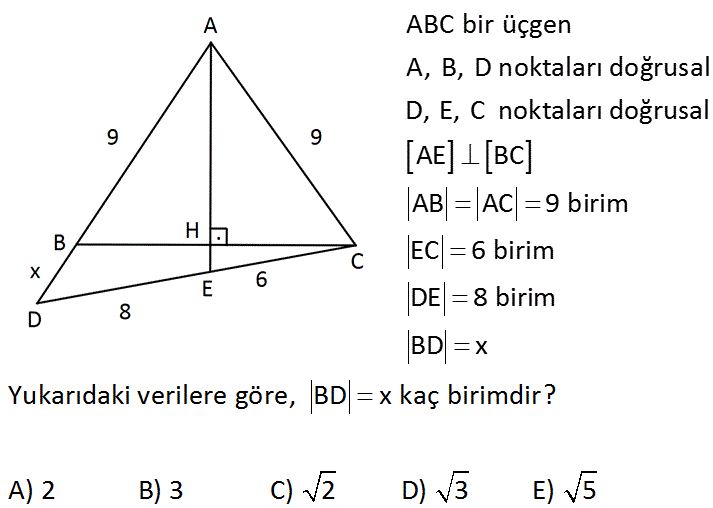
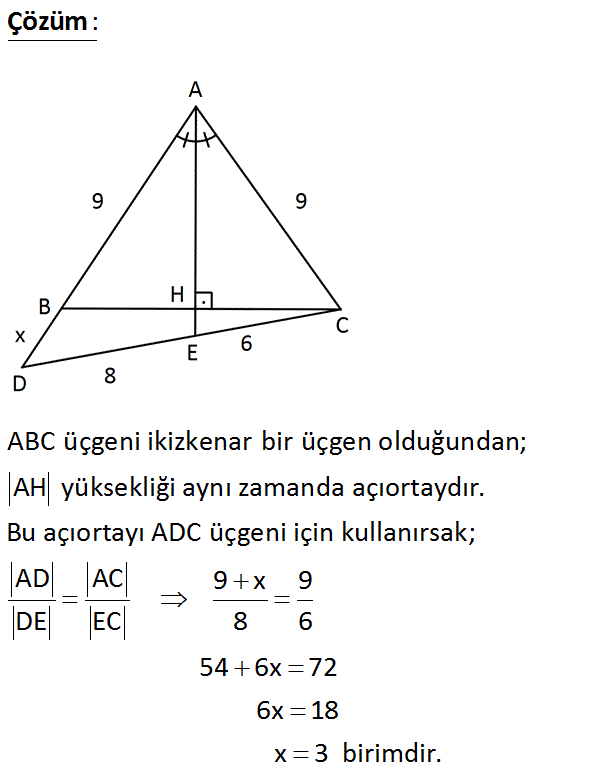
ABC bir üçgen A, B, D noktaları doğrusal D, E, C noktaları doğrusal AE BC AB AC 9 birim EC 6 birim DE 8 birim BD x Yukarıdaki verilere göre, BD x kaç birimdir? A) 2 B) 3 C) 2 D) 3 E) 5 Çözüm: ABC üçgeni ikizkenar bir üçgen olduğundan; AH yüksekliği aynı zamanda açıortaydır. Bu açıortayı ADC üçgeni için kullanırsak; AD AC 9 x 9 DE EC 8 6 54 6x 72 6x 18 x 3 birimdir. 6
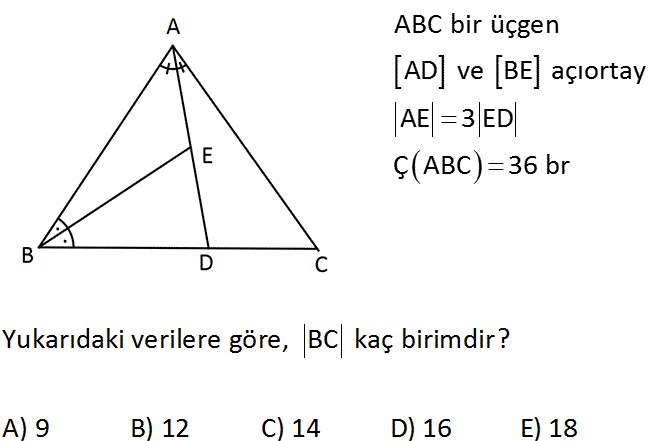
ABC bir üçgen AD ve BE açıortay AE 3 ED Ç ABC 36 br Yukarıdaki verilere göre, BC kaç birimdir? A) 9 B) 12 C) 14 D) 16 E) 18 Çözüm: AE 3 AB 3 olur. BE açıortay olduğundan ED 1 BD 1 AB 3x, BD x olur. AD açıortay olduğundan; AB 3 AC 3 olur. BD 1 DC 1 AC 3t, DC t olur. Ç ABC 4x 4t 36 x t 9 olur. BC x t 9 br olur. 7
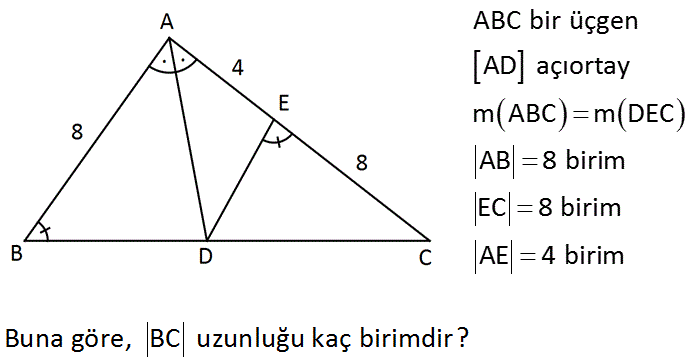
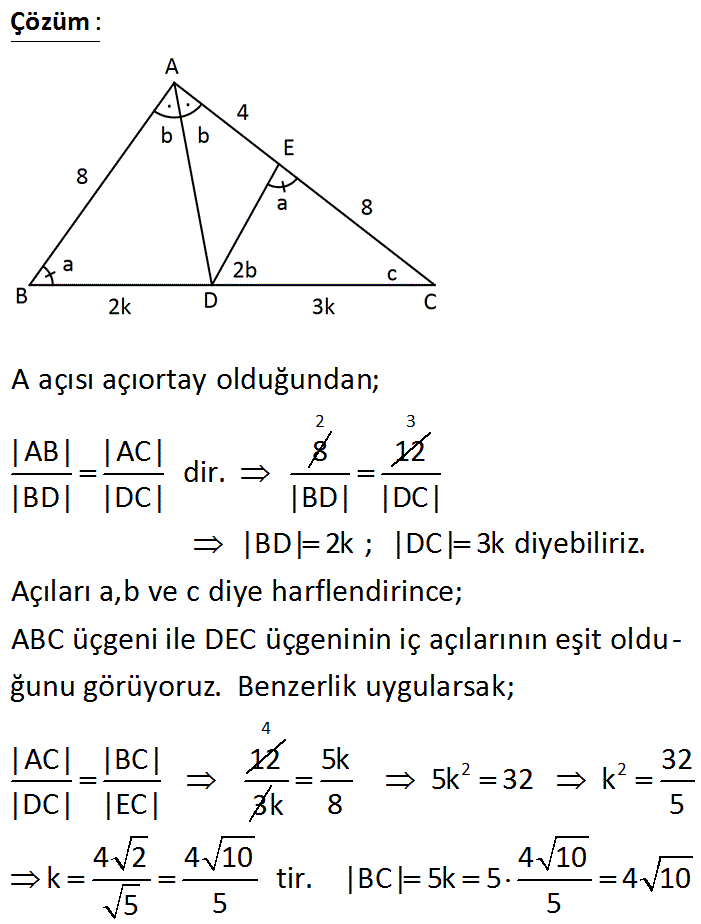
ABC bir üçgen AD açıortay m ABC m DEC AB 8 birim EC 8 birim AE 4 birim Buna göre, BC uzunluğu kaç birimdir? Çözüm: A açısı açıortay olduğundan; |AB| |AC| 8 dir. |BD| |DC| 2 12 |BD| 3 |DC| |BD| 2k ; |DC| 3k diyebiliriz. Açıları a,b ve c diye harflendirince; ABC üçgeni ile DEC üçgeninin iç açılarının eşit oldu – ğunu görüyoruz. Benzerlik uygularsak; |AC| | |BC| 12 DC| |EC| 4 3 2 2 5k 32 5k 32 k k 8 5 4 2 4 10 4 10 k tir. |BC| 5k 5 4 10 5 5 5 21
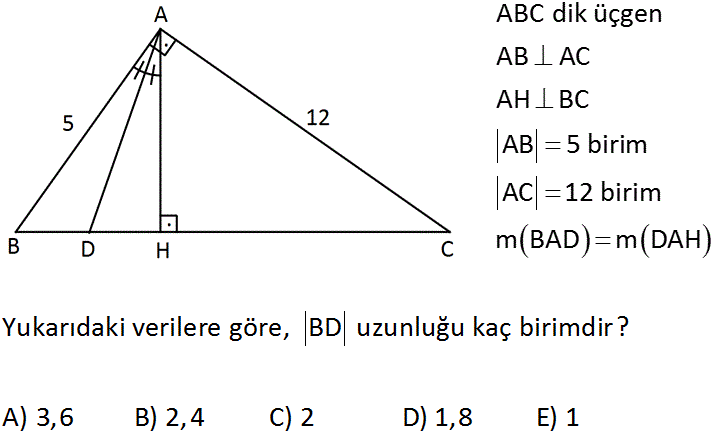
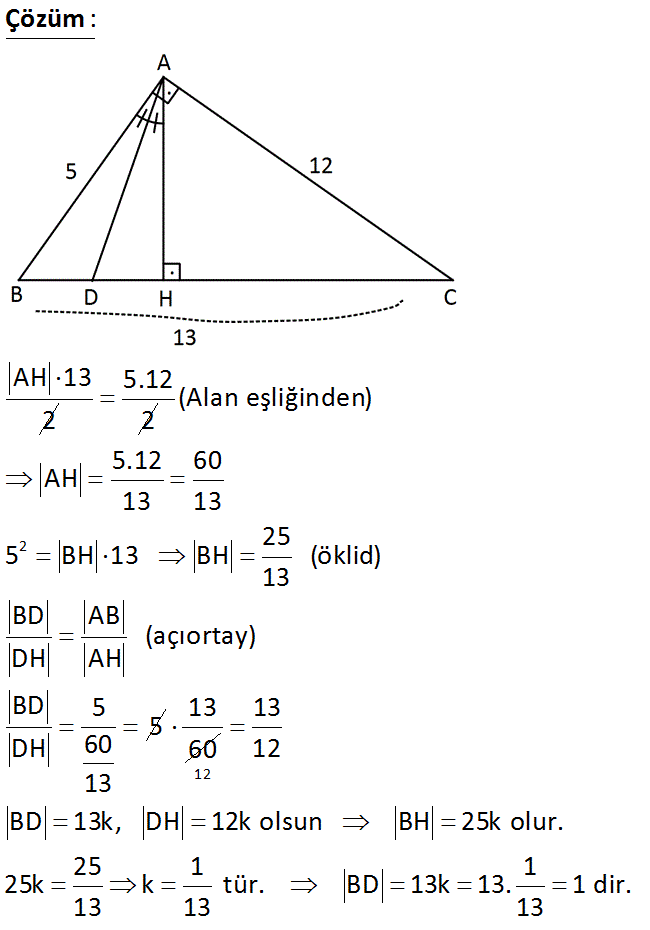
ABC dik üçgen AB AC AH BC AB 5 birim AC 12 birim m BAD m DAH Yukarıdaki verilere göre, BD uzunluğu kaç birimdir? A) 3,6 B) 2,4 C) 2 D) 1,8 E) 1 Çözüm: AH 13 2 5.12 2 2 (Alan eşliğinden) 5.12 60 AH 13 13 25 5 BH 13 BH (öklid) 13 BD AB (açıortay) DH AH BD 5 5 DH 60 13 13 60 12 13 12 BD 13k, DH 12k olsun BH 25k olur. 25 1 1 25k k tür. BD 13k 13. 1 dir. 13 13 13 28
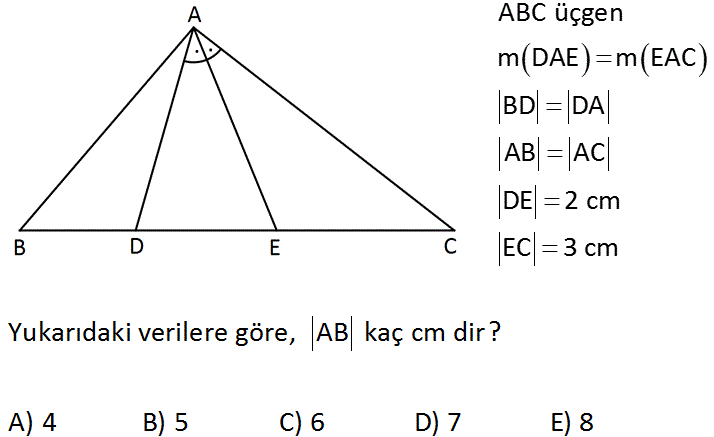
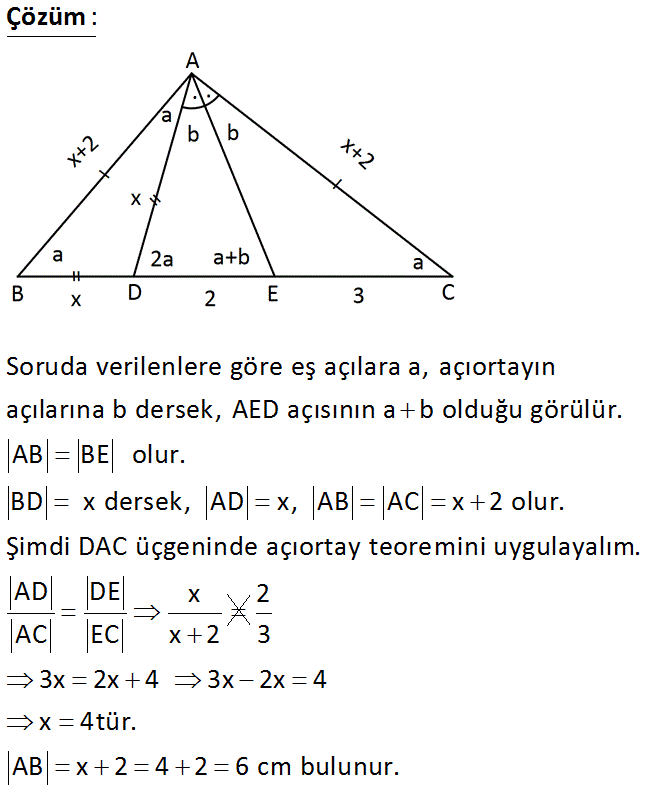
ABC üçgen m DAE m EAC BD DA AB AC DE 2 cm EC 3 cm Yukarıdaki verilere göre, AB kaç cm dir? A) 4 B) 5 C) 6 D) 7 E) 8 : Çözüm Soruda verilenlere göre eş açılara a, açıortayın açılarına b dersek, AED açısının a b olduğu görülür. AB BE olur. BD x dersek, AD x, AB AC x 2 olur. Şimdi DAC üçgeninde açıortay teoremini uygulayalım. A D DE x AC EC x 2 2 3 3x 2x 4 3x 2x 4 x 4tür. AB x 2 4 2 6 cm bulunur. 31
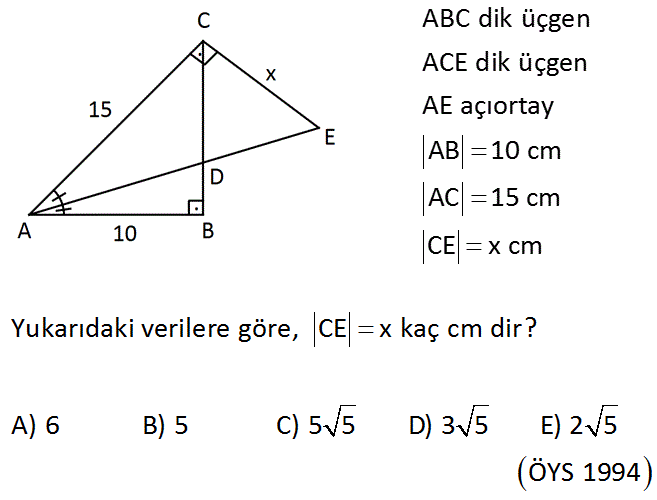
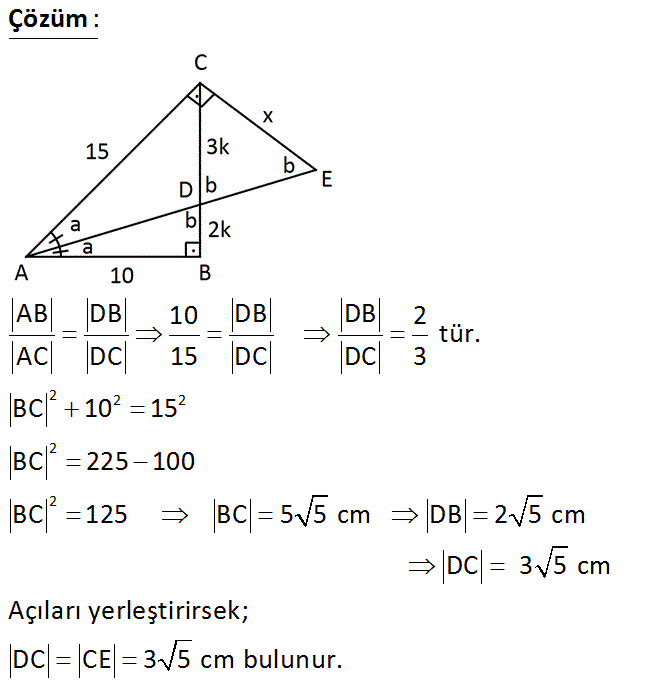
ABC dik üçgen ACE dik üçgen AE açıortay AB 10 cm AC 15 cm CE x cm Yukarıdaki verilere göre, CE x kaç cm dir? A) 6 B) 5 C) 5 5 D) 3 5 E) 2 5 ÖYS 1994 Çözüm: 2 2 2 2 2 AB DB 10 DB DB 2 tür. AC DC 15 DC DC 3 BC 10 15 BC 225 100 BC 125 BC 5 5 cm DB 2 5 cm DC 3 5 cm Açıları yerleştirirsek; DC CE 3 5 cm bul unur. 34
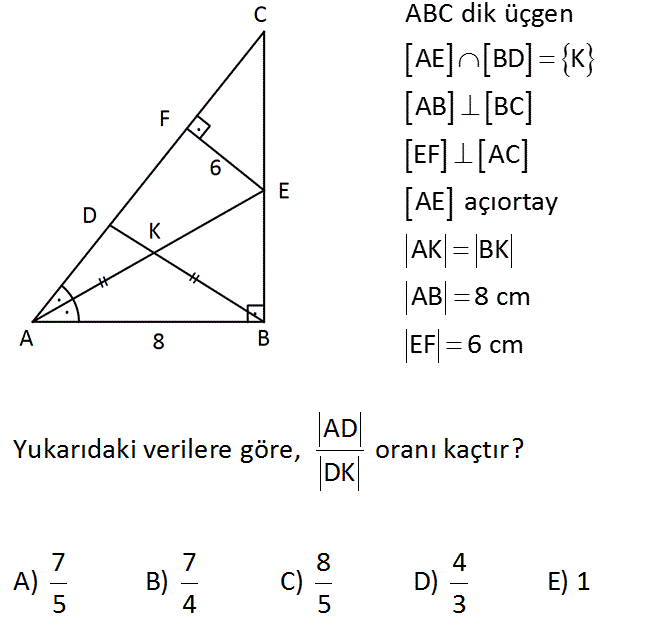
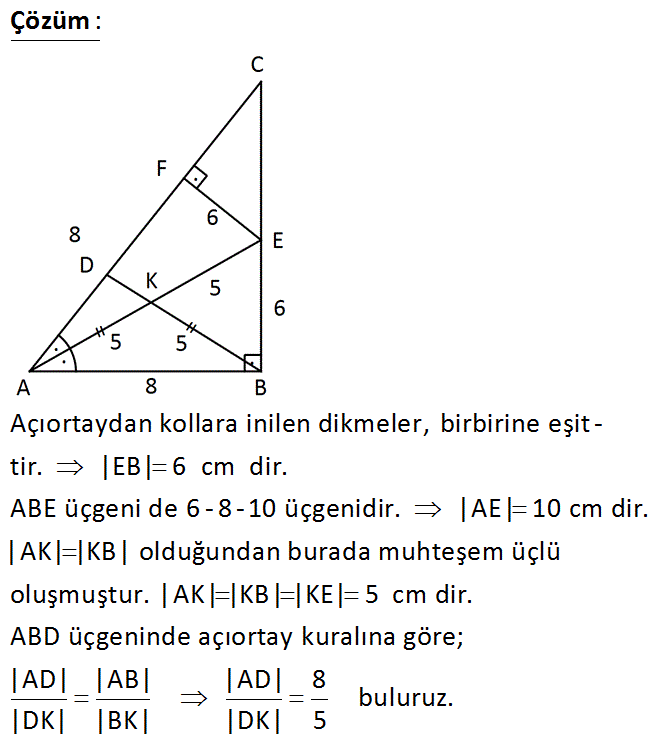
ABC dik üçgen AE BD K AB BC EF AC AE açıortay AK BK AB 8 cm EF 6 cm AD Yukarıdaki verilere göre, oranı kaçtır? DK 7 7 8 4 A) B) C) D) E) 1 5 4 5 3 Çözüm: Açıortaydan kollara inilen dikmeler, birbirine eşit – tir. |EB| 6 cm dir. ABE üçgeni de 6 -8 -10 üçgenidir. |AE| 10 cm dir. |AK| |KB| olduğundan burada muhteşem üçlü oluşmuştur. |AK| |KB| |KE| 5 cm d ir. ABD üçgeninde açıortay kuralına göre; |AD| |AB| |AD| 8 buluruz. |DK| |BK| |DK| 5 35
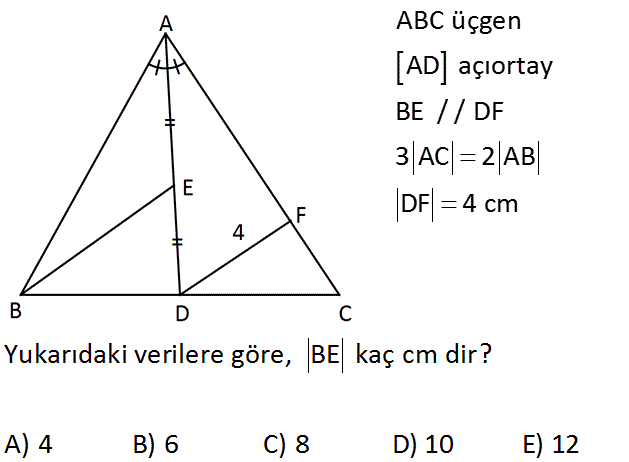
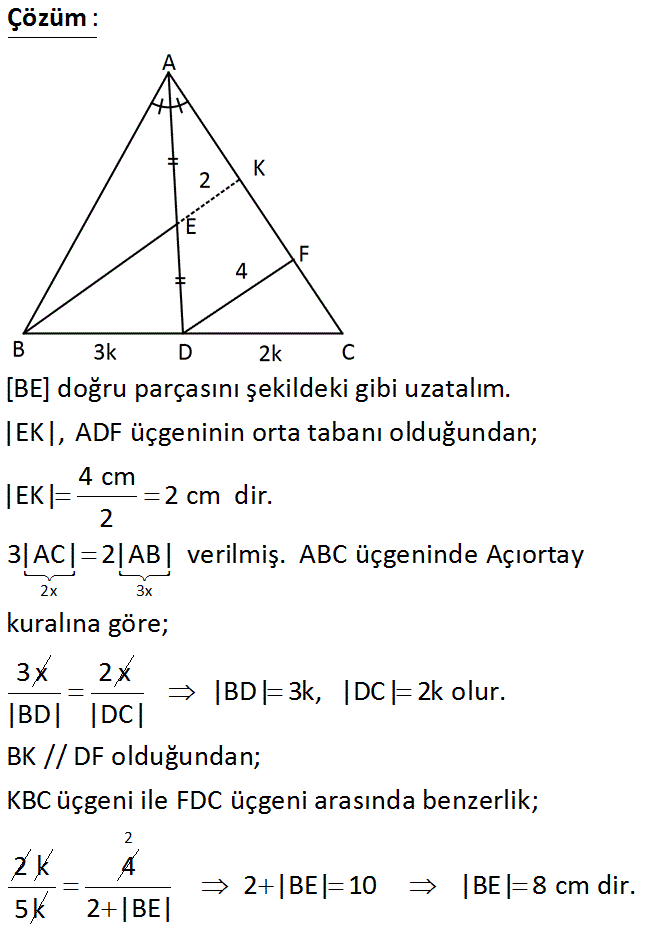
ABC üçgen AD açıortay BE / / DF 3 AC 2 AB DF 4 cm Yukarıdaki verilere göre, BE kaç cm dir? A) 4 B) 6 C) 8 D) 10 E) 12 Çözüm: 2x 3x [BE] doğru parçasını şekildeki gibi uzatalım. |EK|, ADF üçgeninin orta tabanı olduğundan; 4 cm |EK| 2 cm dir. 2 3|AC| 2|AB| verilmiş. ABC üçgeninde Açıortay kuralına göre; 3x 2 x |BD| |BD| 3k, |DC| 2k olur. |DC| BK // DF olduğundan; KBC üçgeni ile FDC üçgeni arasında benzerlik; 2 k 5k 4 2 2 |BE| 10 |BE| 8 cm dir. 2 |BE| 36
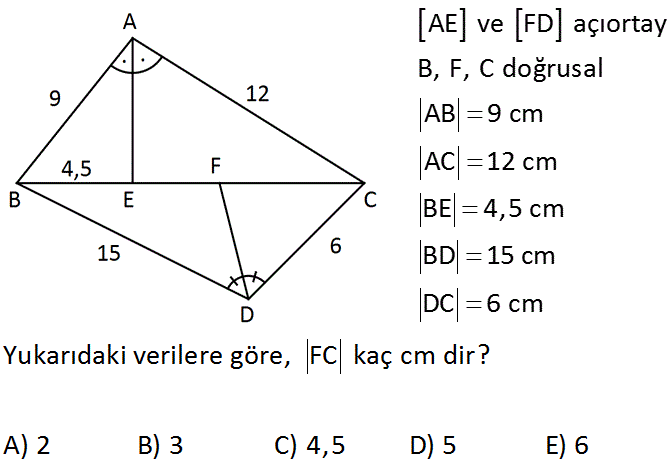
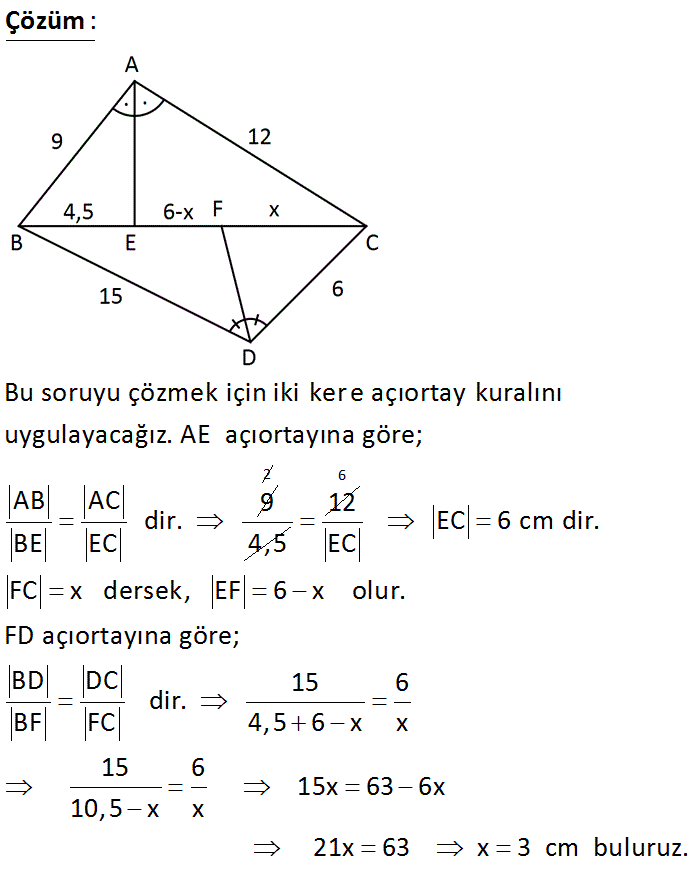
AE ve FD açıortay B, F, C doğrusal AB 9 cm AC 12 cm BE 4,5 cm BD 15 cm DC 6 cm Yukarıdaki verilere göre, FC kaç cm dir? A) 2 B) 3 C) 4,5 D) 5 E) 6 Çözüm: Bu soruyu çözmek için iki kere açıortay kuralını uygulayacağız. AE açıortayına göre; AB AC 9 dir. BE EC 2 4,5 12 6 EC 6 cm dir. EC FC x dersek, EF 6 x olur. FD açıortayına göre; BD DC 15 6 dir. BF FC 4,5 6 x x 15 6 15x 63 6x 10,5 x x 21x 63 x 3 cm b uluruz. 41

