Soru Sor sayfası kullanılarak Üçgende Açıortay konusu altında Dış Açıortay Bağıntısı, Dış Açıortay oranları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

2.SORU
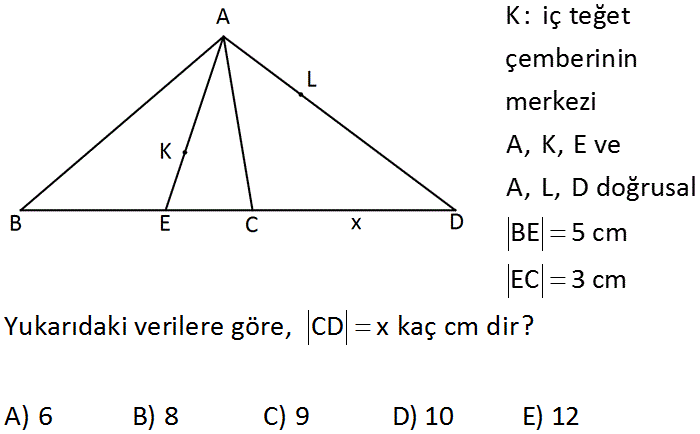
3.SORU
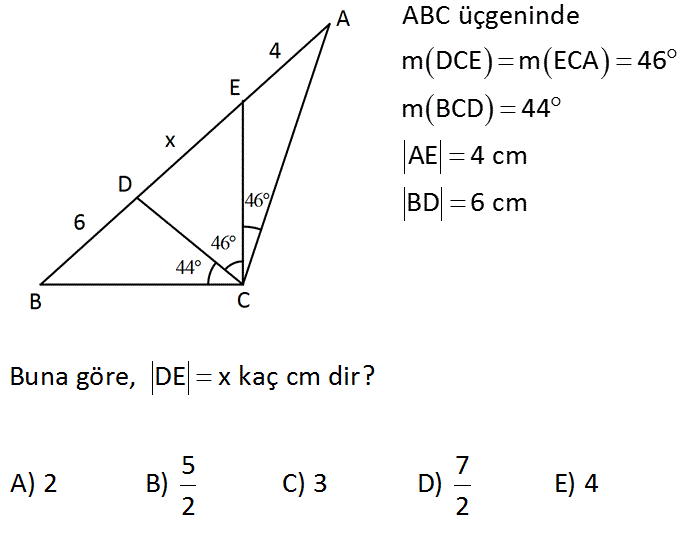
4.SORU

5.SORU
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
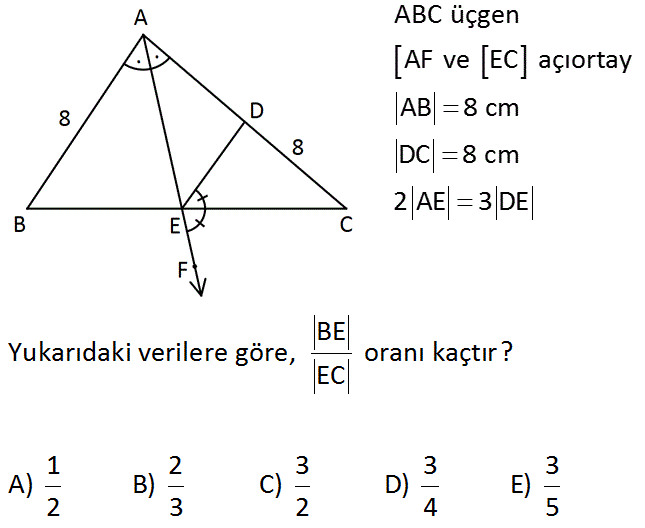
ABC üçgen AF ve EC açıortay AB 8 cm DC 8 cm 2 AE 3 DE BE Yukarıdaki verilere göre, oranı kaçtır? EC 1 2 3 3 3 A) B) C) D) E) 2 3 2 4 5 : Çözüm AEC üçgeninde dış açıortay kuralını uygulayalım. 3x y 8 2x 8 3 2 y 8 2y 16 24 2y 8 y 4 tür. 8 ABC üçgeninde iç açıortay kuralını uygulayalım. AB BE 8 BE BE 2 bulunur. AC EC 12 EC EC 3 44
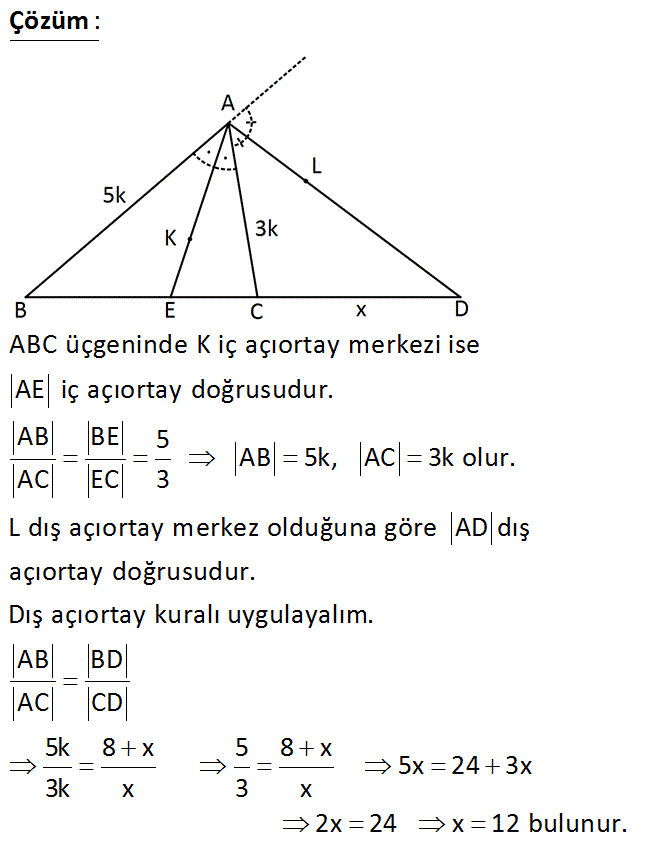
K : iç teğet çemberinin merkezi A, K, E ve A, L, D d oğrusal BE 5 cm EC 3 cm Yukarıdaki verilere göre, CD x kaç cm dir? A) 6 B) 8 C) 9 D) 10 E) 12 : Çözüm ABC üçgeninde K iç açıortay merkezi ise AE iç açıortay doğrusudur. AB BE 5 AB 5k, AC 3k olur. AC EC 3 L dış açıortay merkez olduğuna göre AD dış açıortay doğrusudur. Dış açıortay kuralı uygulayalım. AB B AC D CD 5k 8 x 5 8 x 5x 24 3x 3k x 3 x 2x 24 x 12 bulunur. 45
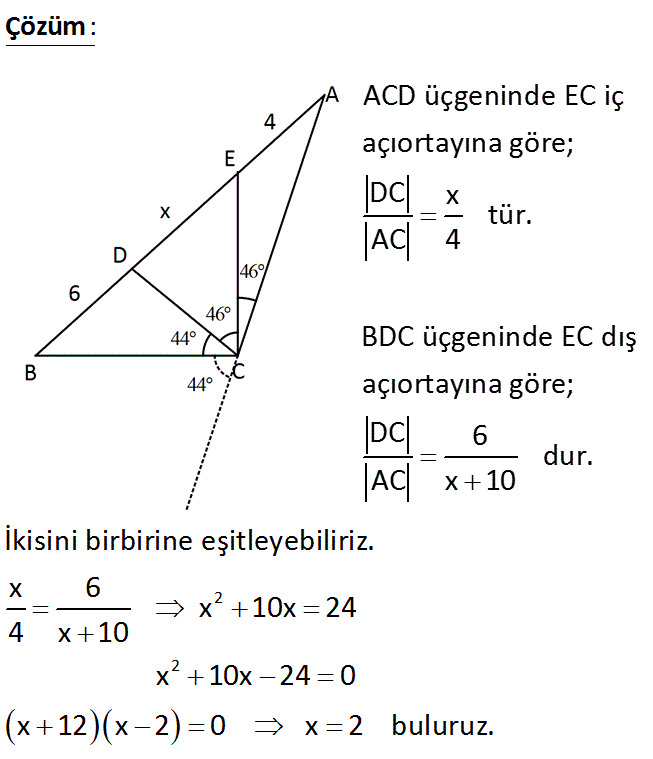
ABC üçgeninde m DCE m ECA 46 m BCD 44 AE 4 cm BD 6 cm Buna göre, DE x kaç cm dir? 5 7 A) 2 B) C) 3 D) E) 4 2 2 : Çözüm ACD üçgeninde EC iç açıortayına göre; DC x tür. AC 4 BDC üçgeninde EC dış açıortayına göre; DC 6 dur. AC x 10 2 2 İkisini birbirine eşitleyebiliriz. x 6 x 10x 24 4 x 10 x 10x 24 0 x 12 x 2 0 x 2 buluruz. 9
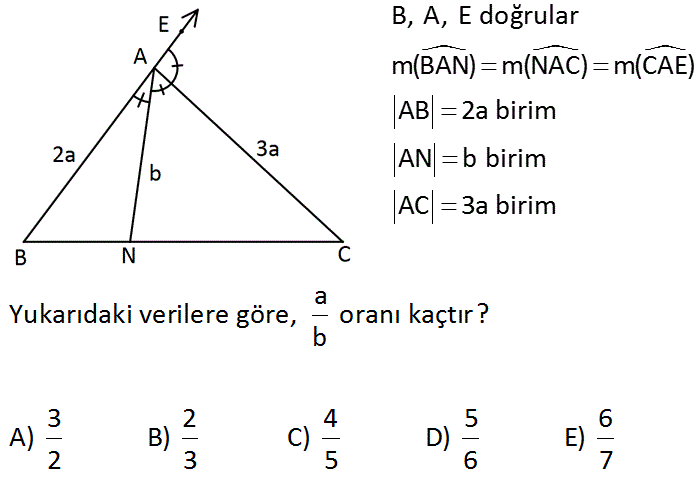
B, A, E doğrular m(BAN) m(NAC) m(CAE) AB 2a birim AN b birim AC 3a birim a Yukarıdaki verilere göre, oranı kaçtır? b 3 2 4 5 6 A) B) C) D) E) 2 3 5 6 7 : Çözüm AN bir iç açıortaydır. İç açıortaya göre; AB AC olmalıdır. BN NC 2a 3a BN BN 2k , NC 3k diyebiliriz. NC Ayrıca, AC doğrusu da ABN üçgeninin bir dış açıortayıdır. Dış açıortaya göre; AB AN olmalıdır. BC NC 2a 5k b 3k a 5 6a 5b buluruz. b 6 46
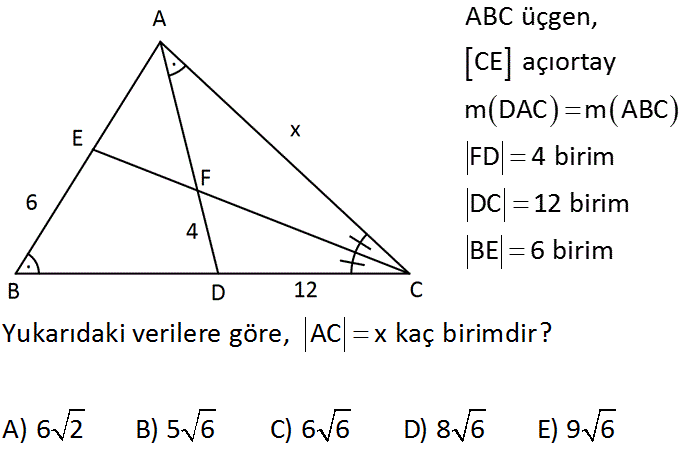
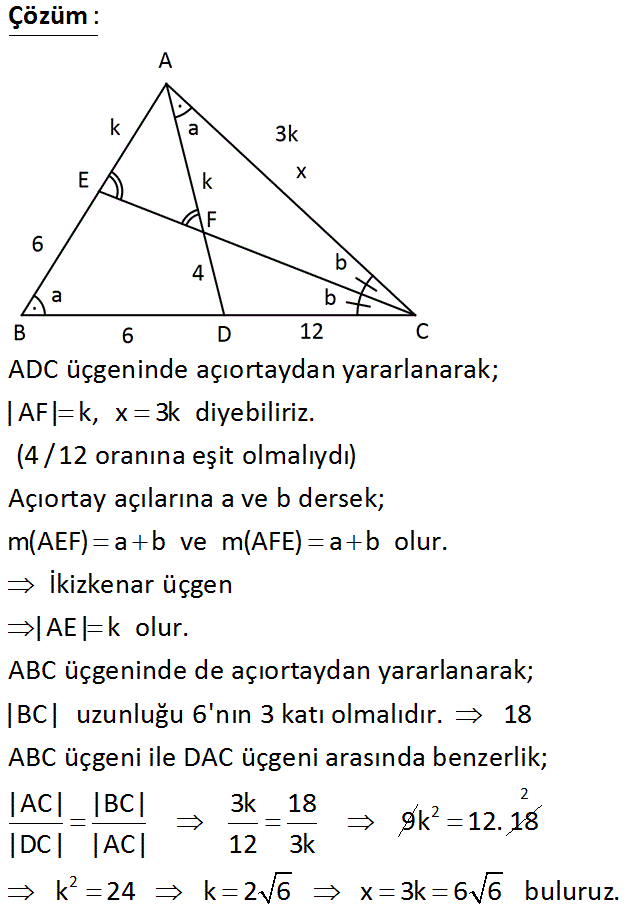
ABC üçgen, CE açıortay m DAC m ABC FD 4 birim DC 12 birim BE 6 birim Yukarıdaki verilere göre, AC x kaç birimdir? A) 6 2 B) 5 6 C) 6 6 D) 8 6 E) 9 6 : Çözüm ADC üçgeninde açıortaydan yararlanarak; |AF| k, x 3k diyebiliriz. (4 /12 oranına eşit olmalıydı) Açıortay açılarına a ve b dersek; m(AEF) a b ve m(AFE) a b olur. İkizkenar üçgen |AE| k olur. ABC üçgeninde de açıortaydan yararlanarak; |BC| uzunluğu 6’nın 3 katı olmalıdır. 18 ABC üçgeni ile DAC üçgeni arasında benzerlik; |AC| |BC| 3k 18 9 |DC| |AC| 12 3k k2 12. 18 2 2 k 24 k 2 6 x 3k 6 6 buluruz. 18

