Soru Sor sayfası kullanılarak Üçgende Açıortay konusu altında Açıortay ve üçgende uzunluk bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

2.SORU

3.SORU

4.SORU
5.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
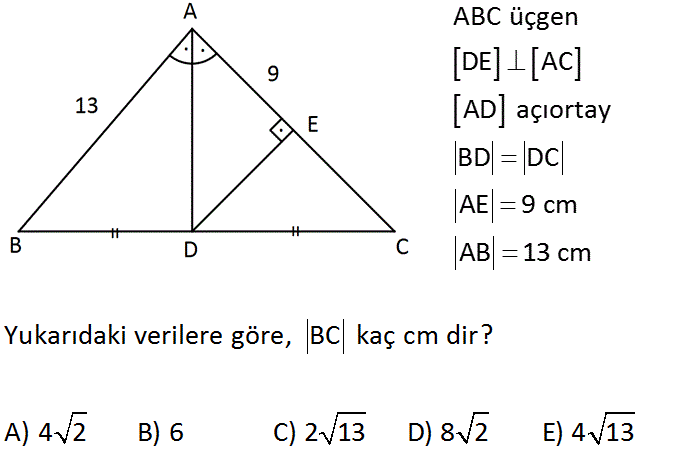
ABC üçgen DE AC AD açıortay BD DC AE 9 cm AB 13 cm Yukarıdaki verilere göre, BC kaç cm dir? A) 4 2 B) 6 C) 2 13 D) 8 2 E) 4 13 : Çözüm 2 2 2 2 Bir üçgende açıortay doğrusu aynı zamanda kenarortaysa;aynı doğru yüksekliktir ve üçgen ikizkenardır.Buna göre; EC 4 cm olur. ADC üçgeninde öklid uygularsak; h 4.9 h 36 h 6 cm olur. DC 6 4 52 2 13 tü r. BC 2 DC BC 4 13 cm bulunur. 23
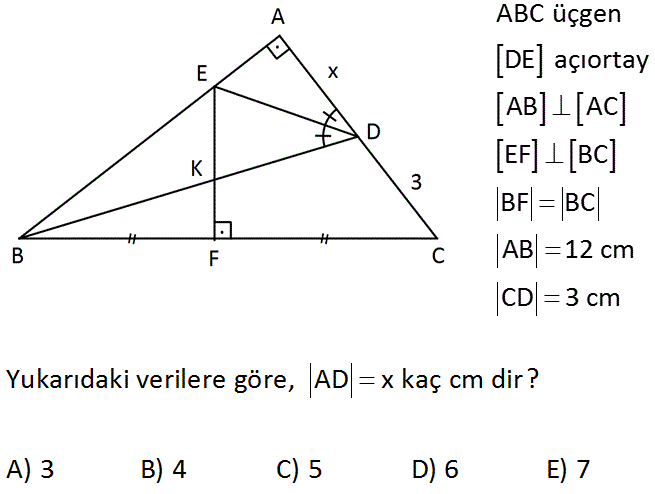
ABC üçgen DE açıortay AB AC EF BC BF BC AB 12 cm CD 3 cm Yukarıdaki verilere göre, AD x kaç cm dir? A) 3 B) 4 C) 5 D) 6 E) 7 : Çözüm FE ‘yi uzatıp, üçgeni tamamlarsak, yükseklik tabanı iki eş parçaya böldüğü için, Üçgen ikizkenar olur. HBD üçgeninde iki açıortay E noktasında kesiştiğine göre diğer açı da açıortaydır. HBD üçgeninde AB do ğrusu hem yükseklik hem açıortay olduğundan üçgen ikizkenar olur. HA x olur. HB 2x 3 olur. ABH üçgenine bakarsak; x 12 2x 3 üçgeninde x 5 olursa 5 12 13 üçgeni olur. x 5 bulunur. 33
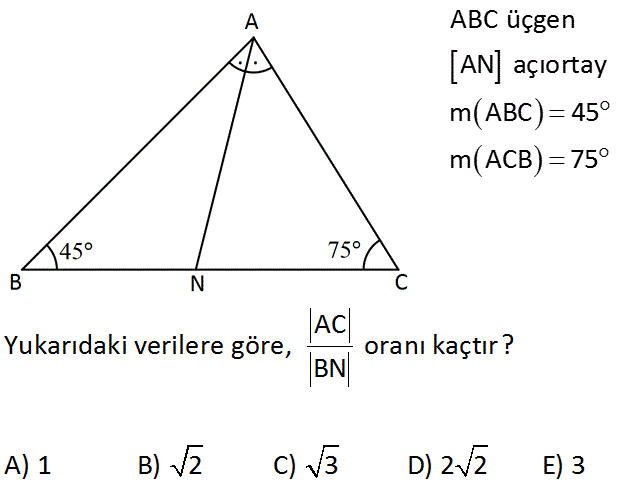
ABC üçgen AN açıortay m ABC 45 m ACB 75 AC Yukarıdaki verilere göre, oranı kaçtır? BN A) 1 B) 2 C) 3 D) 2 2 E) 3 : Çözüm m(BAC) 180 45 75 180 120 60 dir. Açıortay açıları 30 dir. N’den D’ye bir dikme çekelim. BDN üçgeni bir 45- 45-90 üçgenidir. |BD| |DN| k dersek; |BN| k 2 olur. ADN üçgeni de 30 -60 -90 üçgenidir. |AN| 2k olur. m(ANC) 30 45 75 olduğundan; ANC üçgeni bir ikizkenar üçgendir. |AC| 2k olur. O halde; AC 2k 2 buluruz. BN k 2 37
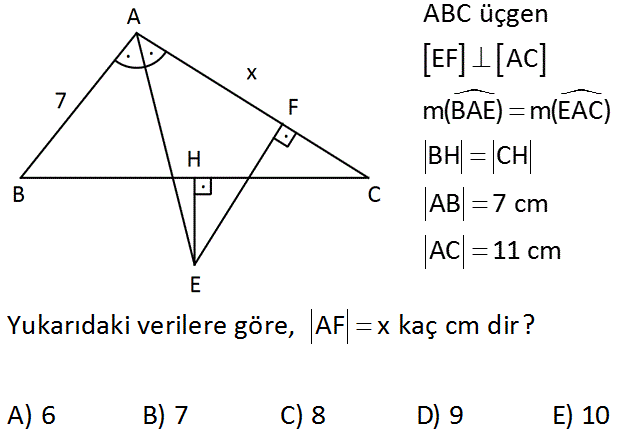
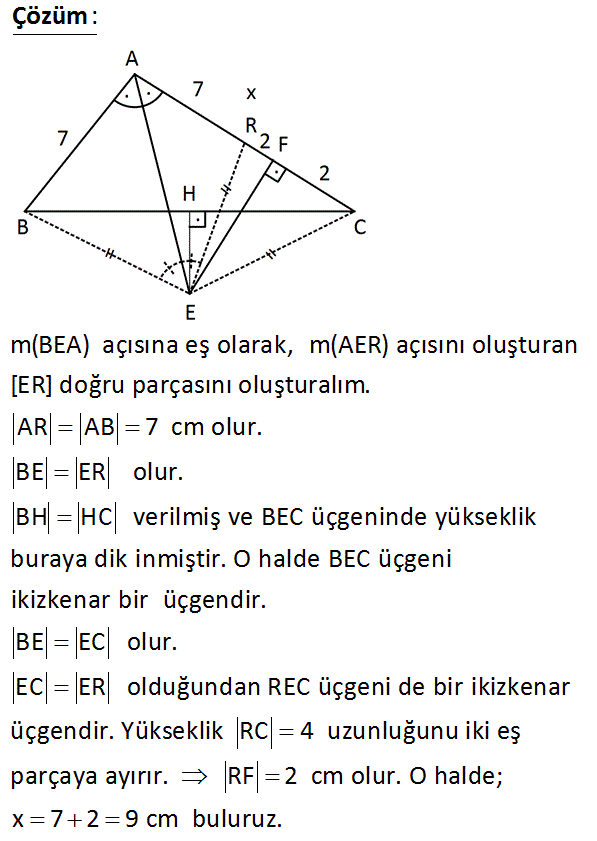
ABC üçgen EF AC m(BAE) m(EAC) BH CH AB 7 cm AC 11 cm Yukarıdaki verilere göre, AF x kaç cm dir? A) 6 B) 7 C) 8 D) 9 E) 10 : Çözüm m(BEA) açısına eş olarak, m(AER) açısını oluşturan [ER] doğru parçasını oluşturalım. AR AB 7 cm olur. BE ER olur. BH HC verilmiş ve BEC üçgeninde yükseklik buraya dik inmiştir. O halde BEC üçgeni ik izkenar bir üçgendir. BE EC olur. EC ER olduğundan REC üçgeni de bir ikizkenar üçgendir. Yükseklik RC 4 uzunluğunu iki eş parçaya ayırır. RF 2 cm olur. O halde; x 7 2 9 cm buluruz. 42
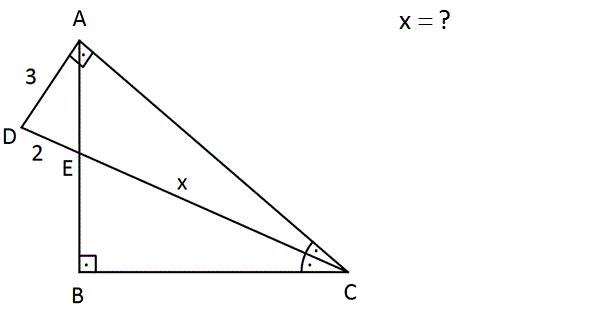
x? Çözüm: Açıortayın açılarına a derece diyelim. m(BEC) b olsun. a b 90 dir. ADC üçgeninin açılarına göre m(ADC) b olmalıdır. m(AED) m(BEC) b dir. O halde; ADE üçgeni ikizkenar bir üçgendir, AE 3 birim olu 2 2 r. A’dan H’ye dikme indirelim. DH HE 1 olur. Pisagordan; AH 3 1 2 2 dir. Öklitten; AH DH . HC 8 1. HC HC 8 birim olur. x 8 1 7 birim buluruz. 48

