Orta taban ile açı kenar bağıntısı, Paralel çizerek kenarı bulma

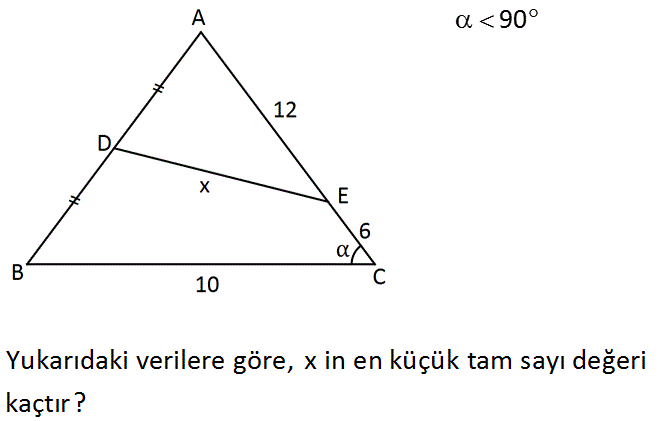
  90 Yukarıdaki verilere göre, x in en küçük tam sayı değeri kaçtır? www.matematikkolay.net : Çözüm 2 2 2 2 2 [BC]’ ye paralel D köşesinden bir doğru çekelim. Bu doğru 5 birim olur. [AC] kenarı da iki eş parçaya ayrılır. Buradan |FE| 3 birim olur. m(DFE) 90 olduğundan, x 5 3 x 25 9 x 34 x en az 6 olmalıdır.       15
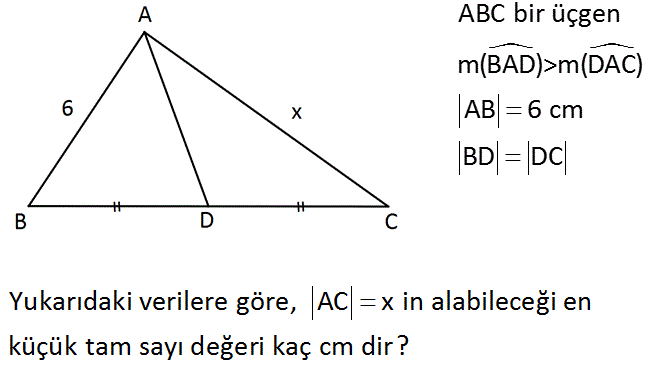
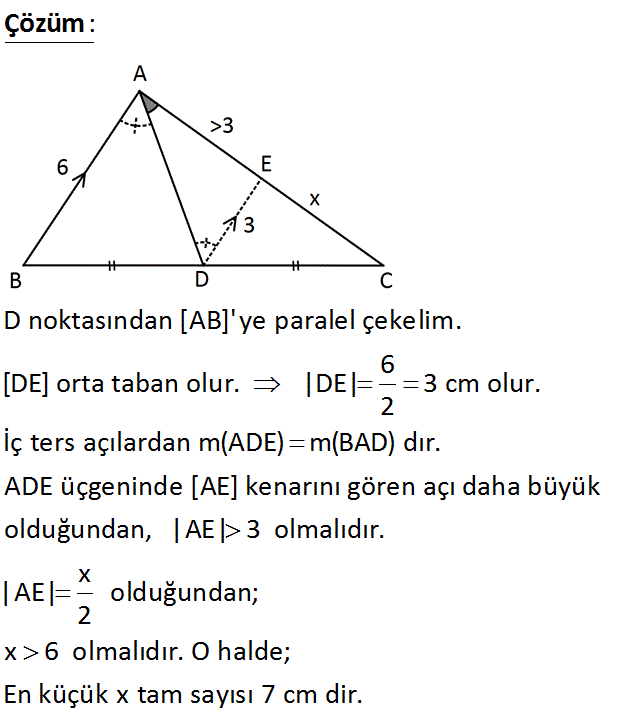
ABC bir üçgen m(BAD)>m(DAC) AB 6 cm BD DC Yukarıdaki verilere göre, AC x in alabileceği en küçük tam sayı değeri kaç cm dir? www.matematikkolay.net : Çözüm D noktasından [AB]’ ye paralel çekelim. 6 [DE] orta taban olur. |DE| 3 cm olur. 2 İç ters açılardan m(ADE) m(BAD) dır. ADE üçgeninde [AE] kenarını gören açı daha büyük olduğundan, |AE| 3 olmalıdır. |AE|   x olduğundan; 2 x 6 olmalıdır. O halde; En küçük x tam sayısı 7 cm dir.  17
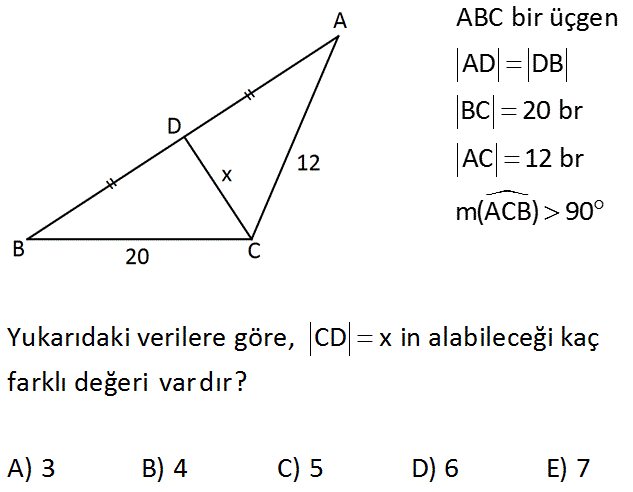
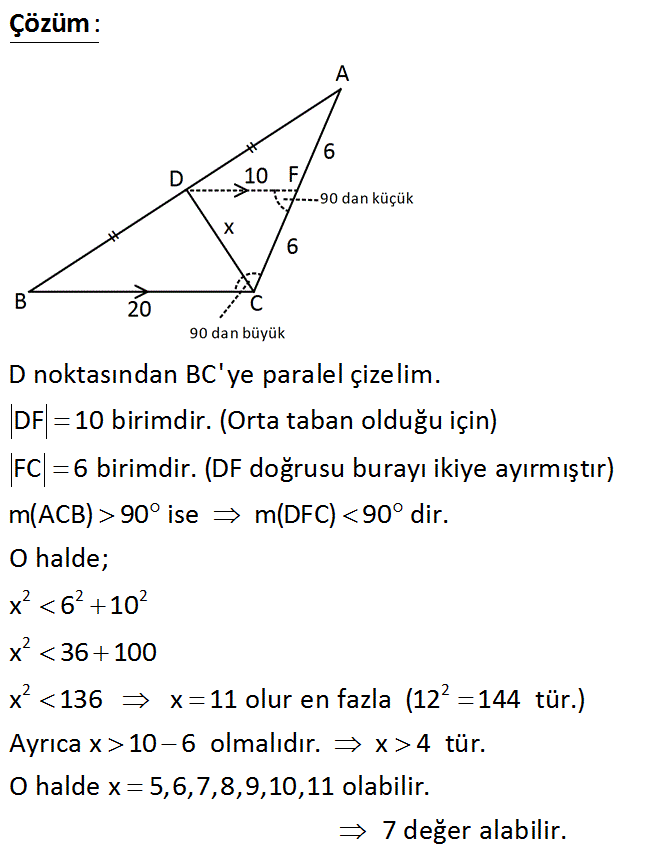
ABC bir üçgen AD DB BC 20 br AC 12 br m(ACB) 90   Yukarıdaki verilere göre, CD x in alabileceği kaç farklı değeri var dır? A) 3 B) 4 C) 5 D) 6 E) 7 Çözüm: www.matematikkolay.net 2 2 2 2 2 D noktasından BC’ ye paralel çizelim. DF 10 birimdir. (Orta taban olduğu için) FC 6 birimdir. (DF doğrusu burayı ikiye ayırmıştır) m(ACB) 90 ise m(DFC) 90 dir. O halde; x 6 10 x 36 100 x 136 x 11            2 olur en fazla (12 144 tür.) Ayrıca x 10 6 olmalıdır. x 4 tür. O halde x 5,6,7,8,9,10,11 olabilir. 7 değer alabilir.      25
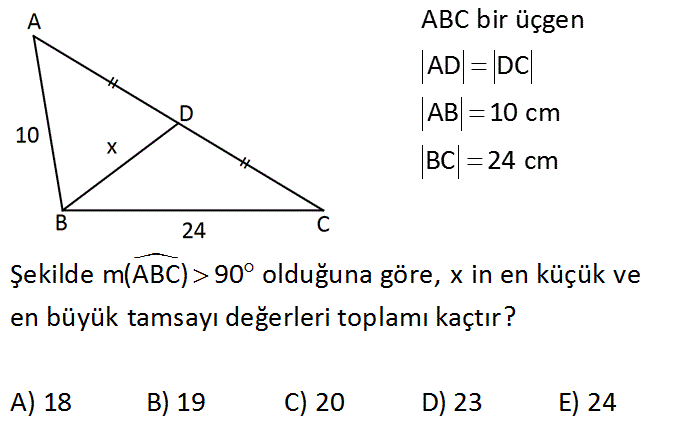
ABC bir üçgen AD DC AB 10 cm BC 24 cm Şekilde m(ABC) 90 olduğuna göre, x in en küçük ve en büyük tamsayı değerleri toplamı kaçtır? A) 18 B) 19 C) 20 D) 23 E) 24   www.matematikkolay.net Çözüm:   2 2 2 2 AB’ye paralel olacak şekilde DE’ yi çizelim. AD DC olduğundan; 10 DE orta tabandır ve DE 5 cm olur. 2 24 BE 12 cm olur. 2 m(ABC) 90 ise m(DEC) 90 dır. Yöndeş açılar m(BED) 90 olur. O halde; x BE DE x       2 2 2 2 12 5 x 144 25 x 169 x 13 tür. En fazla 12 olabilir. BDE üçgenine göre ; x 12 5 x 7 olmalıdır. En az 8 olabilir. Bu değerlerin toplamını 8 12 20 buluruz.            39
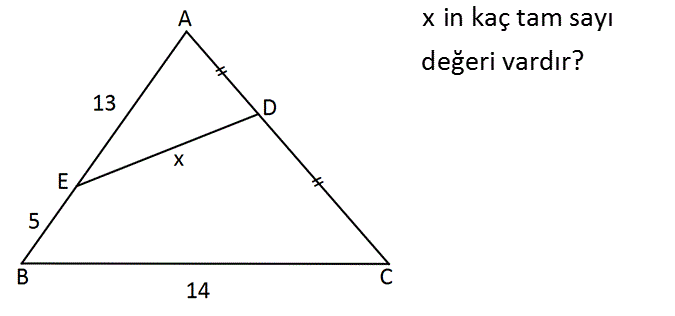
x in kaç tam sayı değeri vardır? Çözüm: www.matematikkolay.net BC ye paralel olarak FD yi çizelim. FD orta taban olur. FD 7 dir. AB kenarı da iki parçaya ayrılır. AF 9 ve FB 9 birim olur. FE 13 9 4 birim kalır. EFD üçgenine göre; 7 4 x 7 4 3 x 11 olmalıdır.        x  4,5,6,7,8,9,10  7 tam sayı değeri 45
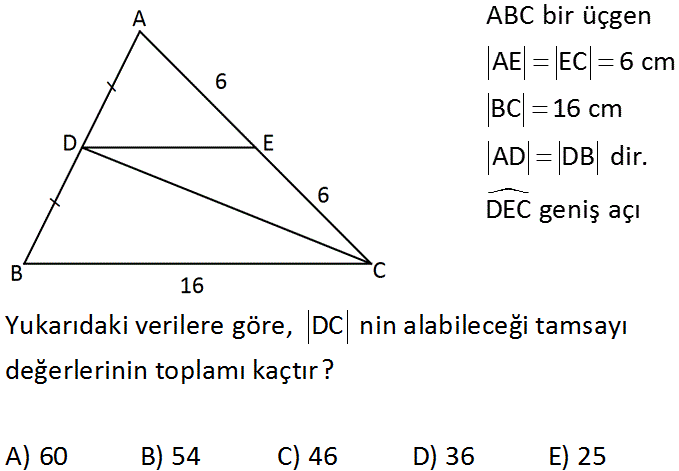
ABC bir üçgen AE EC 6 cm BC 16 cm AD DB dir. DEC geniş açı www.matematikkolay.net Yukarıdaki verilere göre, DC nin alabileceği tamsayı değerlerinin toplamı kaçtır? A) 60 B) 54 C) 46 D) 36 E) 25 2 2 2 2 2 2 2 2 DE uzunluğu, ABC üçgeninin orta tabanıdır. 16 Dolayısıyla DE 8 cm dir. 2 DEC üçgeninde E açısı geniş açı ise, DC DE EC olmalıdır. DC 8 6 DC 64 36 DC 100 DC 10 dur. Ayrıca bir üçgenin kenarı, :         Çözüm diğer iki kenarın topla – mından fazla olamaz. Yani; DC 6 8 DC 14 tür. Buna göre; DC 11,12 ve 13 olabilir. Toplarsak; 11 12 13 36 buluruz.      
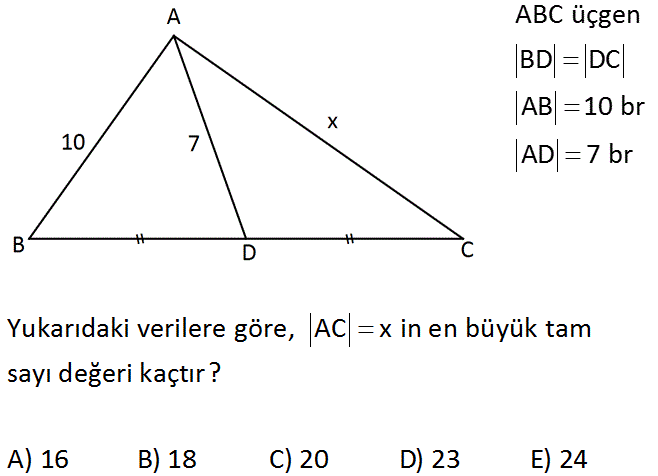
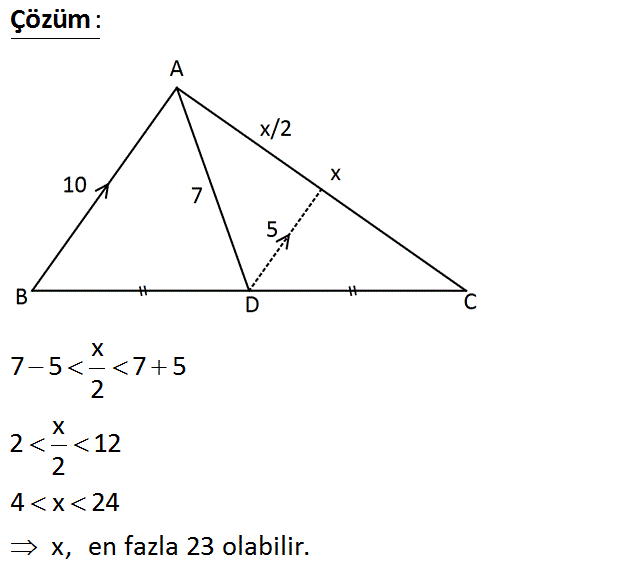
ABC üçgen BD DC AB 10 br AD 7 br Yukarıdaki verilere göre, AC x in en büyük tam sayı değeri kaçtır? A) 16 B) 18 C) 20 D) 23 E) 24 : Çözüm x 7 5 7 5 2 x 2 12 2 4 x 24 x, en fazla 23 olabilir.          2
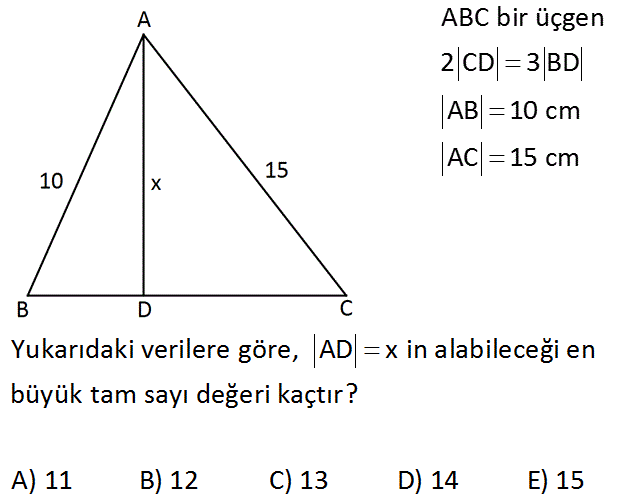
www.matematikkolay.net ABC bir üçgen 2 CD 3 BD AB 10 cm AC 15 cm Yukarıdaki verilere göre, AD x in alabileceği en büyük tam sayı değeri kaçtır? A) 11 B) 12 C) 13 D) 14 E) 15 Çözüm: 2|CD| 3|BD| ise |CD| 3k ve |BD| 2k diyebi – liriz. D köşesinden [AB]’ ye paralel çizersek, ABC üçgeni ile benzer bir üçgen elde ederiz. Benzerlikten; 3k |EC| |EC| 9 ve |AE| 6 cm buluruz. 5k 15 3k 5k  |DE| |DE| 6 cm buluruz. 10 ADE üçgenine göre; x 6 6 x 12 dir. En büyük tam sayı değerini 11 cm buluruz.       www.matematikkolay.net 9
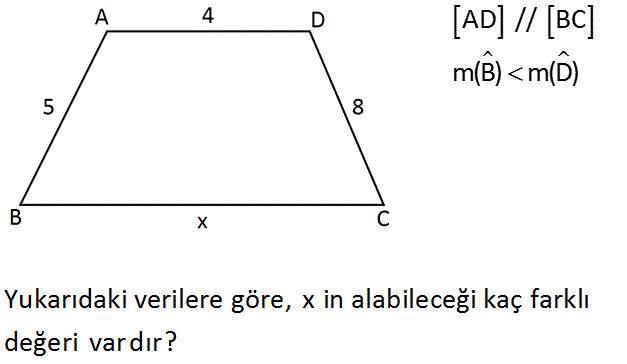
    AD // BC m(B) m(D)  Yukarıdaki verilere göre, x in alabileceği kaç farklı değeri var dır? : Çözüm m(B) m(D) ise AB’ye paralel olarak DE yi çizdiğimizde bir DEC üçgeni oluşabilmelidir. 8 5 |EC| 8 5 3 |EC| 13 |EC| 4,5,6,7,8,9,10,11,12 9 farklı değer x değeri de 9 farklı değer alacaktır.          22