Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında Yerel Ekstremum, Yerel Maksimum, Yerel Minimum
ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU

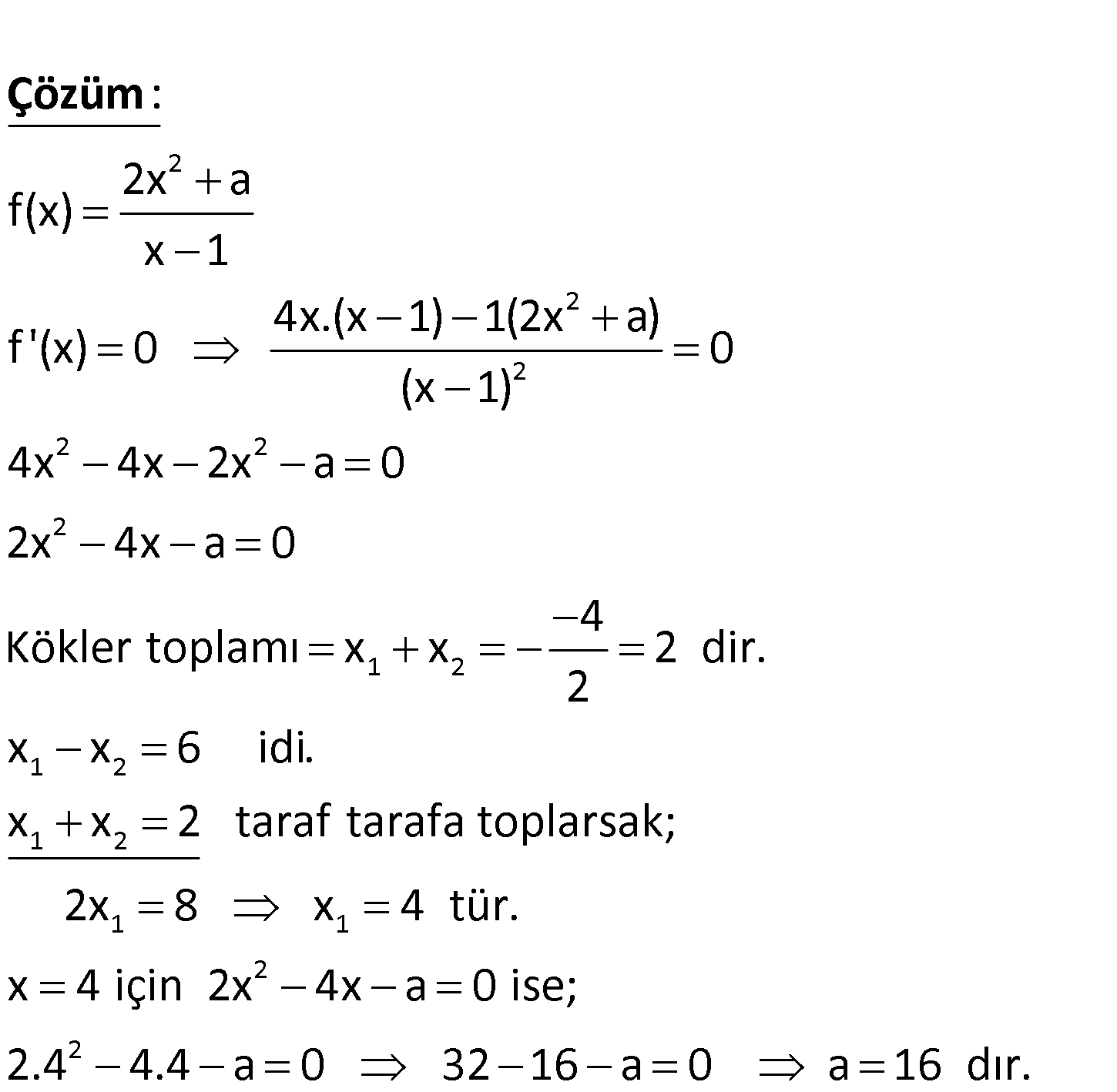
4.SORU


5.SORU

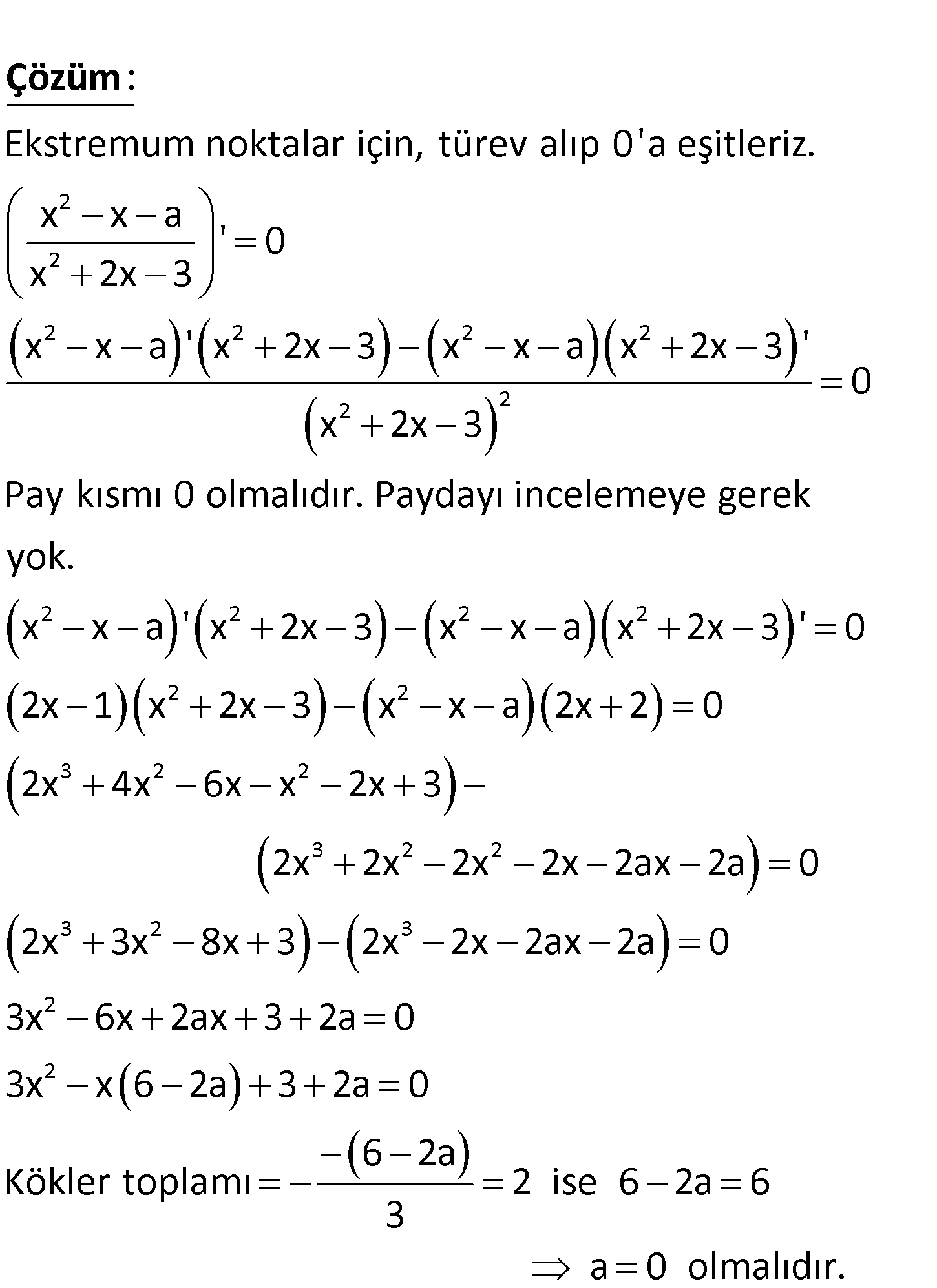
6.SORU


7.SORU

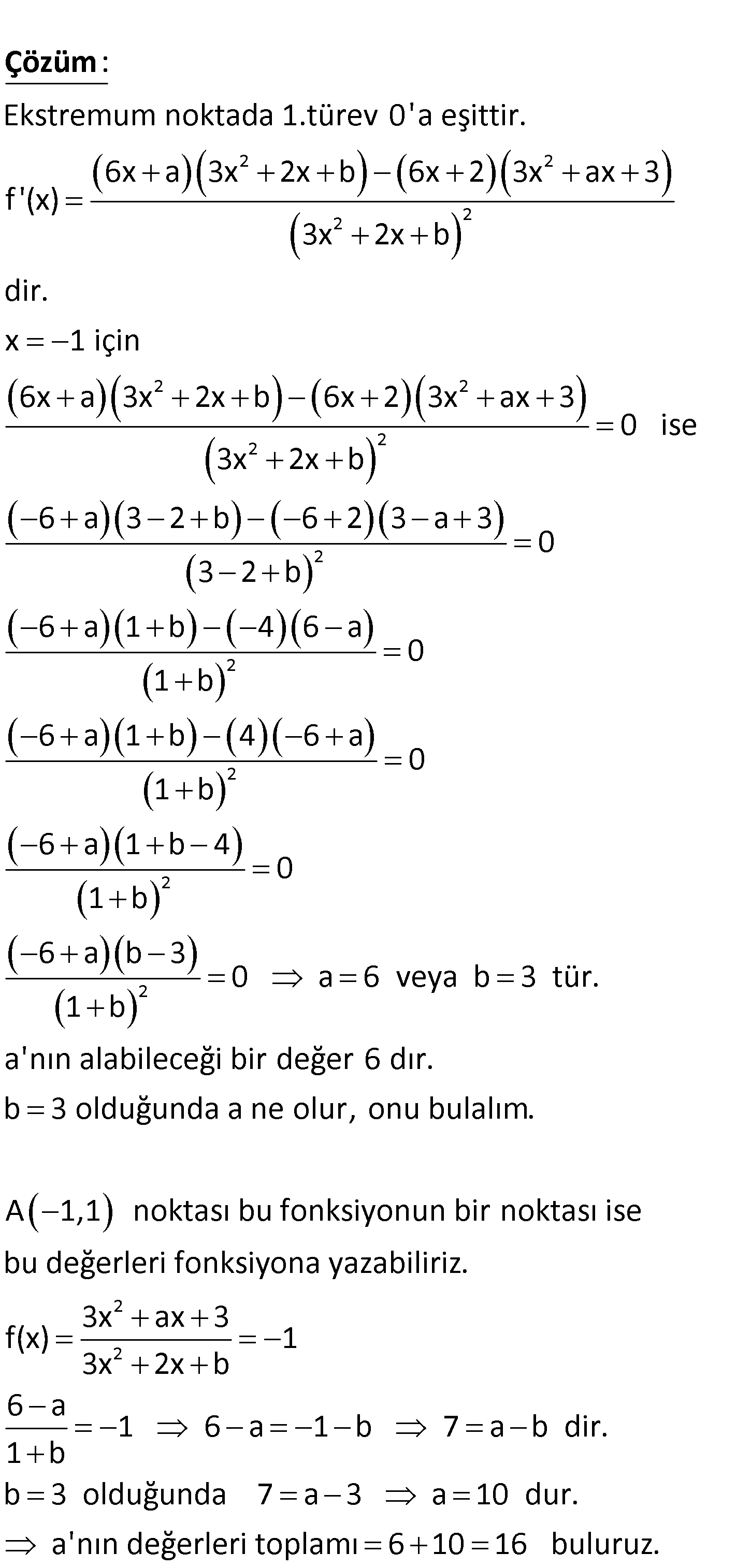
8.SORU


9.SORU

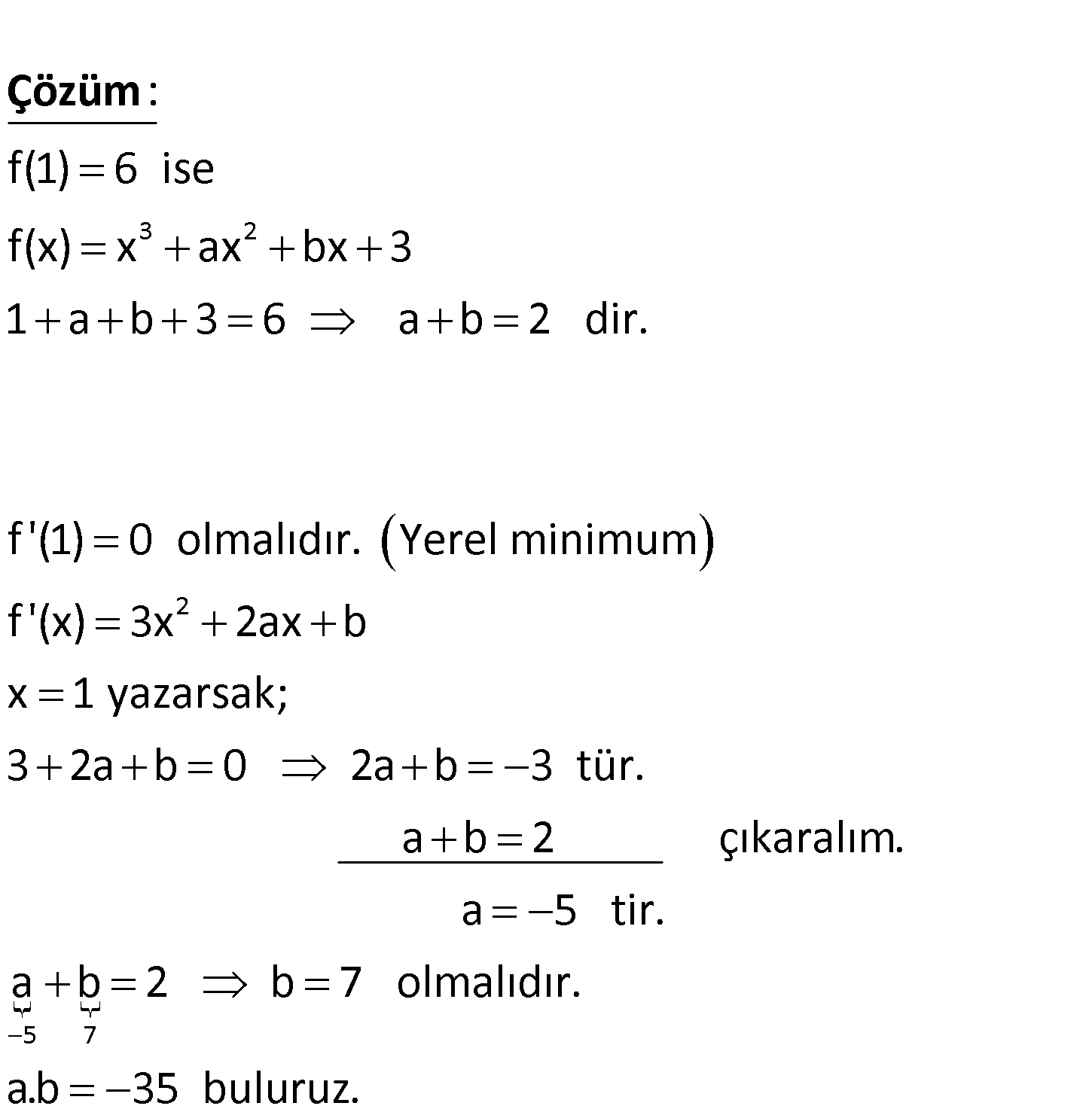
10.SORU
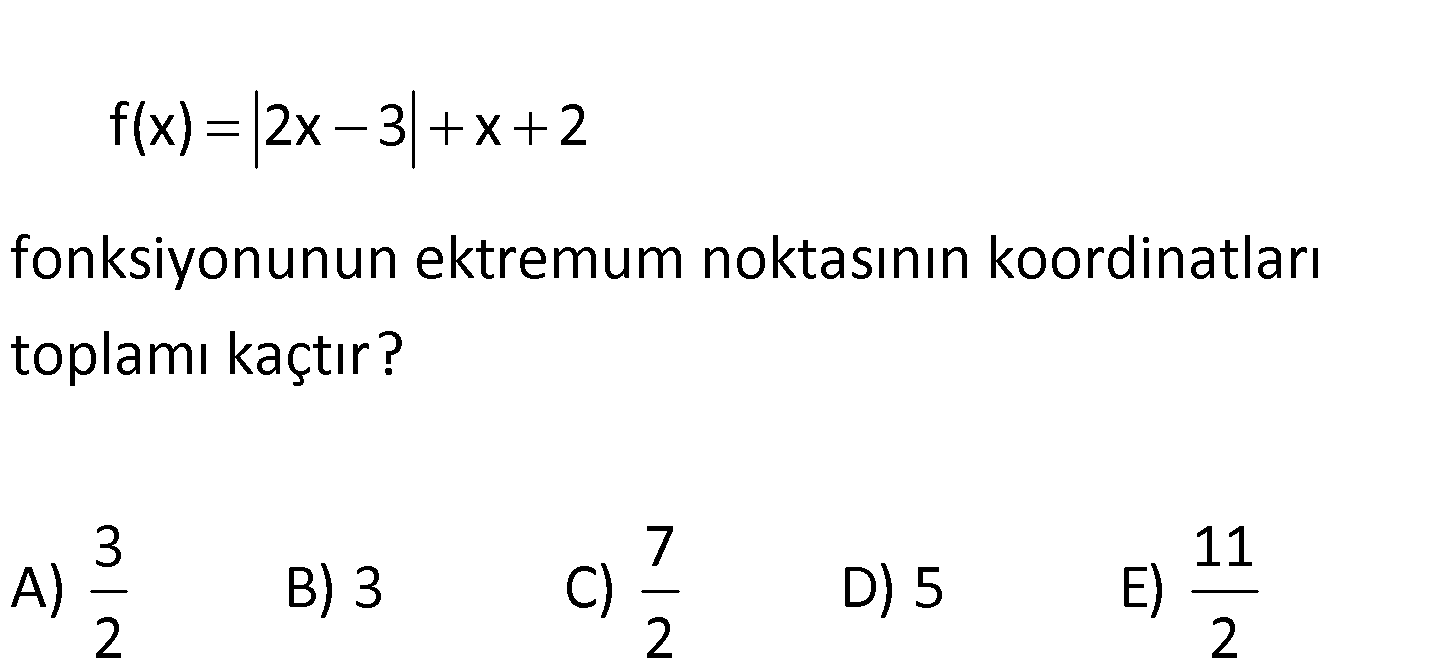

11.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3 f(x) x mx n eğrisinin ( 1, 5) noktasında yerel ekstremumu olduğuna göre, m.n çarpımı kaçtır ? www.matematikkolay.net 3 2 f(x) x mx n yerel ekstremum noktasında türev, 0’a eşittir. Buna göre; f ‘( 1) 0 dır. 3x m 0 : 3 Çözüm 3 m 0 m 3 tür. ( 1,5) noktası, f(x)’in bir noktası olduğundan; f( 1) 5 x 3x n 5 1 3 n 5 n 3 tür. m.n 3.3 9 buluruz. 64
2 x x f(x) x m fonksiyonunun A(1, n) noktasında bir ekstremum olduğuna göre, m.n çarpımı kaçt ır? 1 2 4 A) 1 B) C) D) E)2 3 3 3 2 2 Ekstremum noktalarda türev 0’a eşittir. (2x 1)(x m) (1)(x x) f ‘(x) (x m) x 1 içi : n f ‘(x) 0 o Çözüm 2 2 2 2 lmalıdır. (2 1)(1 m) (1)(1 1) 3 3m 2 f ‘(1) 0 0 (1 m) (1 m) 1 3m 1 0 1 3m 0 m buluruz. (1 m) 3 x 1 için fonksiyon hangi değeri almış, bulalım. x x 1 1 2 f(1) 3 tür. (n 3 tür.) x m 1 2 1 3 3 Buna göre 1 ; m.n 3 1 buluruz. 3 73
2 1 2 2 1 2x a f(x) fonksiyonunun ekstremum noktaları – x 1 nın apsisleri x ve x dir. x x 6 olduğuna gör e, a kaçtır? A) 16 B) 12 C) 10 D) 8 E) 4 2 2 2 2 2 2 1 2x a f(x) x 1 4x.(x 1) 1(2x a) f ‘(x) 0 0 (x 1) 4x 4x 2x a 0 2x 4x a 0 Kökler toplamı x : x Çözüm 2 1 2 1 2 1 1 2 2 4 2 dir. 2 x x 6 idi. x x 2 taraf tarafa toplarsak; 2x 8 x 4 tür. x 4 için 2x 4x a 0 ise; 2.4 4.4 a 0 32 16 a 0 a 16 dır. www.matematikkolay.net 87
www.matematikkolay.net Başkatsayısı 1 olan üçüncü dereceden gerçel katsayılı bir P(x) polinom fonksiyonunun köklerinden ikisi 2 ve 3 tür. P(x) in x 1 noktasında bir yerel ekstremumı oldu – ğuna göre, üçüncü kök kaçtır? 1 1 2 A) 3 B) 2 C) D) E) 2 3 3 P(x) (x 2)(x 3)(x a) şeklinde bir polinomdur. P'(x) (x 3)(x a) (x 2)(x a) (x 3)(x 2) P'(1) 0 : Çözüm ise; (1 3)(1 a) (1 2)(1 a) (1 3)(1 2) 0 2 2a 1 a 2 0 3a 1 1 a buluruz. 3 95
www.matematikkolay.net 2 2 x x a y eğrisinin yerel maksimum ve yerel x 2x 3 minimum noktalarının apsisleri toplamının 2 olm ası için a kaç olmalıdır? A) 6 B) 4 C) 2 D) 1 E) 0 2 2 2 2 2 Ekstremum noktalar için, türev alıp 0’a eşitleriz. x x a ‘ 0 x 2x 3 x x a ‘ x 2x 3 x x : Çözüm 2 2 2 2 2 2 2 2 2 3 2 2 3 2 2 3 a x 2x 3 ‘ 0 x 2x 3 Pay kısmı 0 olmalıdır. Paydayı incelemeye gerek yok. x x a ‘ x 2x 3 x x a x 2x 3 ‘ 0 2x 1 x 2x 3 x x a 2x 2 0 2x 4x 6x x 2x 3 2x 2x 2x 2x 2ax 2a 0 2x 3 2 3 2 2 x 8x 3 2x 2x 2ax 2a 0 3x 6x 2ax 3 2a 0 3x x 6 2a 3 2a 0 6 2a Kökler toplamı 2 ise 6 2a 6 3 a 0 olmalıdır. www.matematikkolay.net 135
2 f(x) x 8x 7 fonksiyonunun yerel minimu m nokt ası hangisi i d r? 2 : Türevini 0’a eşitleyerek kritik noktayı bulalım. f ‘(x) 2x 8 0 x 4 tür. x 4 için f(x 8x ) x Çözüm 7 f(4) 16 32 7 9 Tek bir kritik nokta var. Bu da yerel minimum noktasıdır zaten. Bu nok tanın koordinatı da (4, 9) dur. 14
www.matematikkolay.net 2 2 fonksiyonunun A( 1, 1) noktası bir yerel 3x ax 3 f( extre – mum nokta x) 3 sı x 2x olduğuna g b öre, a nın alabileceği değerlerin toplamı kaçtır? A) 8 B) 12 C) 16 D) 20 E) 24 www.matematikkolay.net 2 2 2 2 Ekstremum noktada 1.türev 0’a eşittir. 6x a 3x 2x b 6x 2 3x ax 3 f ‘(x) 3x 2x b dir. x 1 i : çi Çözüm 2 2 2 2 2 2 2 2 2 n 6x a 3x 2x b 6x 2 3x ax 3 0 ise 3x 2x b 6 a 3 2 b 6 2 3 a 3 0 3 2 b 6 a 1 b 4 6 a 0 1 b 6 a 1 b 4 6 a 0 1 b 6 a 1 b 4 0 1 b 6 a b 3 0 a 6 veya b 3 tür. 1 b a’nın alabileceği bir değer 6 dır. b 3 ol 2 2 duğunda a ne olur, onu bulalım. A 1,1 noktası bu fonksiyonun bir noktası ise bu değerleri fonksiyona yazabiliriz. 3x ax 3 f(x) 1 3x 2x b 6:00 AM 1 6 a 1 b 7 a b dir. 1 b b 3 olduğunda 7 a 3 a 10 dur. a’nın değerleri toplamı 6 10 16 buluruz. www.matematikkolay.net 154
2 3 ax b y eğrisi (1, 2) noktasında yerel maksimum x değerini alıyorsa b kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 3 3 1,2 noktasını denkleme yazalım. a b 2 a b 2 dir. 1 x 1 için, türevi 0 olmalıdır. Yerel : Çözüm 2 3 2 2 3 3 1 maksimum 2ax.x ax b .1 y’ x x 1 yazalım. 2a a b 0 olmalıdır. 2a 2 0 a 1 1 a b 2 idi. b 1 olmalıdır. 187
www.matematikkolay.net 3 2 f(x) x ax bx 3 fonksiyonu A(1, 6) noktasında yerel minimuma sahip olduğuna göre, a.b çarpı – m ının sonucu kaçtır? A) 30 B) 32 C) 35 D) 38 E) 40 3 2 f(1) 6 ise f(x) x ax bx 3 1 a b 3 6 a b 2 dir. f ‘(1) 0 olmalıdır. Yerel minimum f ‘(x) : Çözüm 2 5 7 3x 2ax b x 1 yazarsak; 3 2a b 0 2a b 3 tür. a b 2 çıkaralım. a 5 tir. a b 2 b 7 olmalıdır. a.b 35 buluruz. 195
f(x) 2x 3 x 2 fonksiyonunun ektremum noktasının koordinatları toplamı kaçtır? 3 7 A) B) 3 C) D) 2 2 11 5 E) 2 www.matematikkolay.net f(x) |2x 3| x 2 3 x için f(x) 2x 3 x 2 2 f(x) x 5 f ‘(x) 1 azal : an 3 x Çözüm için f(x) 2x 3 x 2 2 f(x) 3x 1 f ‘(x) 3 ar tan Azalanlık tan artanlığa geçiş var. 3 Ekstremum nokta x ‘de olur. 2 3 3 7 x için f(x) 0 2 dir. 2 2 2 3 7 10 Koordinat toplamı: 5 b 2 2 2 uluruz. 45
www.matematikkolay.net 3 2 f ‘(x) fonksiyonunun yerel minimu f(x) x 6x 3x 1 ise m değeri kaçtır? A) 21 B) 15 , C) 12 D) 9 E) 3 2 f ‘ x 3x 12x 3 Soruda bu fonksiyonun yerel minimum değeri soruluyor. f(x) in değil Tekra : r türev Çözüm 2 2 alarak, minimum değerin nerde olduğunu bulalım. 3x 12x 3 ‘ 0 6x 12 0 6x 12 x 2 dir. x 2 için 3x 12x 3 3.4 24 3 12 24 3 12 3 15 buluruz. 157

