Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında Teğetin kestiği diğer nokta ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU


5.SORU

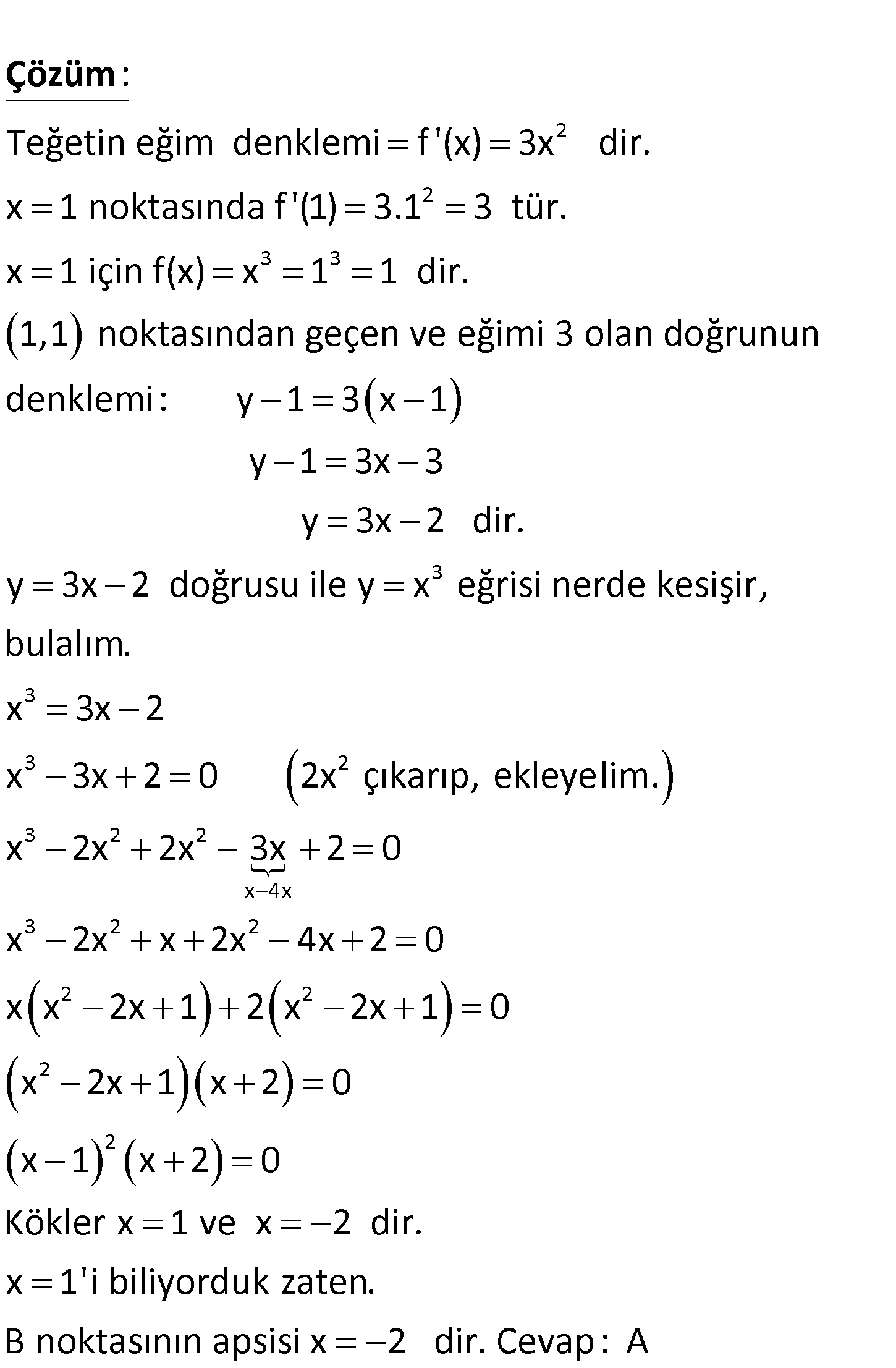
6.SORU


Burdan sonraki sorular, Fen Lisesi Müfredatı için geçerlidir.
7.SORU

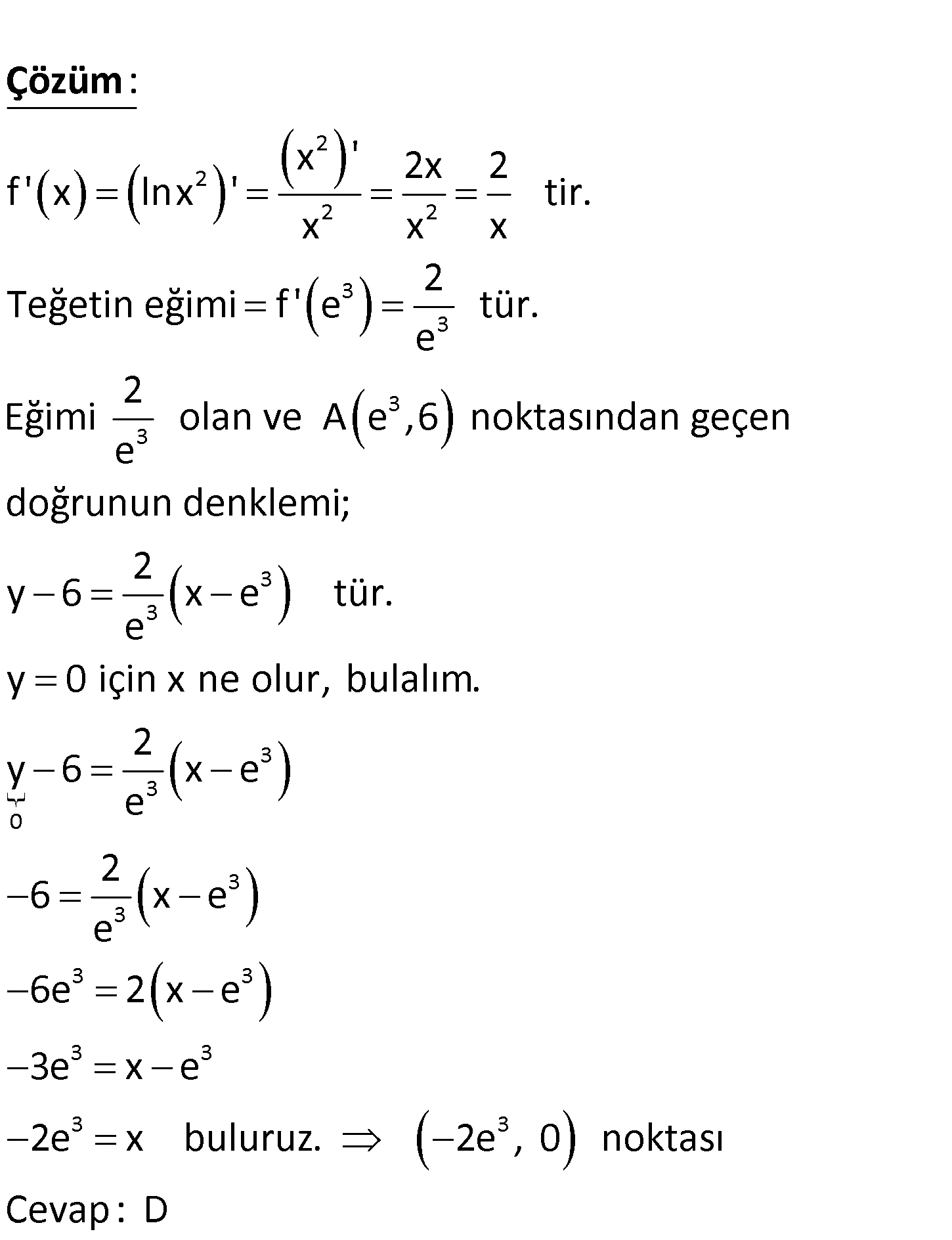
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3 2 y x 4x eğrisinin x 2 deki teğeti, eğriyi P(m,n) noktasında kesiyor. Buna göre, m ka A çtır? ) 2 B) 1 C) 0 D) 1 E) 2 www.matematikkolay.net 2 2 İlk türev, teğetin eğimini verir. y’ 3x 8x x 2 için y’ 3.2 8.2 12 16 4 tür. (eğim) x : Çözüm 3 2 3 2 3 2 3 2 2 için y x 4x 2 4.2 8 4.4 0 dır. Eğimi 4 olan ve (2,0) noktasından geçen doğru – nun denklemi; y 0 4(x 2) y 4x tir. y x 4x ile y 4x in kesişim noktası; x 4x 4x 3 2 2 2 teğet nok. x 4x 4x 0 x(x 4x 4) 0 x( x 2 ) 0 x 0 noktasında kesiyor. m 0 buluruz. 63
3 2 f(x) x x 3x eğrisinin başlangıç noktasındaki teğetinin eğriyi kestiği diğer nok tanın apsisi kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 2 f ‘(x) 3x 2x 3 Teğetin eğimi: f ‘(0) 3 tür. 0 noktasındaki y değeri f(0) 0 dır. Buna göre; : te Çözüm 3 2 ğet denklemi y 3x tir. Diğer noktayı bulmak için, ortak çözüm yapalım. y 3x yazarak x’i bulabiliriz. y x x 3x 3x x3 x2 3x 2 0 x (x 1) x 1 buluruz. 71
2 y f(x) x 4x 3 eğrisinin x 1 apsisli noktasın – daki teğeti, tepe noktasından çizilen teğeti K nok – tasında kesiyor. K noktasının apsisi kaçtır? 1 1 1 1 1 A) B) C) D) E) 3 4 5 2 12 www.matematikkolay.net 2 Teğetin eğimi f ‘( 1) 2x 4 2 4 6 dır. f( 1) x 4x 3 1 4 3 8 dir. ( 1,8) noktasından geç : en Çözüm 2 ve eğimi 6 olan doğru; y 8 6(x ( 1)) y 8 6x 6 y 6x 2 dir. b 4 Parabolün tepe noktası 2 2a 2 f(2) x 4x 3 4 8 3 1 dir. y 1 doğrusu ile y 6x 2 nin kesişimini bulalım. 1 1 6x 2 6x 3 x bulur 2 uz. 80
www.matematikkolay.net 2 x Yukarıdaki grafikte y parabolü ve bu parabolün 4 A(4, 4) noktasındaki teğeti verilmiştir. Buna gör e, bu teğetin B(7, 0) noktasına en yakın olduğu nok tanın apsisi kaçtır? 5 7 9 A) B) 3 C) D) 4 E) 2 2 2 : Çözüm www.matematikkolay.net Parabolün x 4 noktasındaki türevi, teğetin eğimidir. 2x x y’ dir. 4 2 4 x 4 noktasında y ‘ 2 dir. Te 2 ğetin eğimi 4, 4 noktasından geçen ve eğimi 2 olan doğru y 4 2 x 4 y 4 2x 8 y 2x 4 0 dır. Teğetin denklemi En yakın uzaklık için bu doğruya bir dik çizmeliyiz. Dik doğruların eğimleri çarpımı 1 olduğundan bu dikmenin eğimi, 1 m.2 1 m olmalıdır. 2 1 7, 0 noktasından geçen ve eğimi olan doğru 2 1 y 0 x 7 2 7 x y dir. Dikmenin denklemi 2 Teğet denklemi ile kesiştiği yeri bulmak için, bu değeri teğet denklem inde yazalım. 7 x y 2x 4 0 2x 4 0 2 7 x 4x 8 15 5x 0 0 2 2 x 3 buluruz. 150
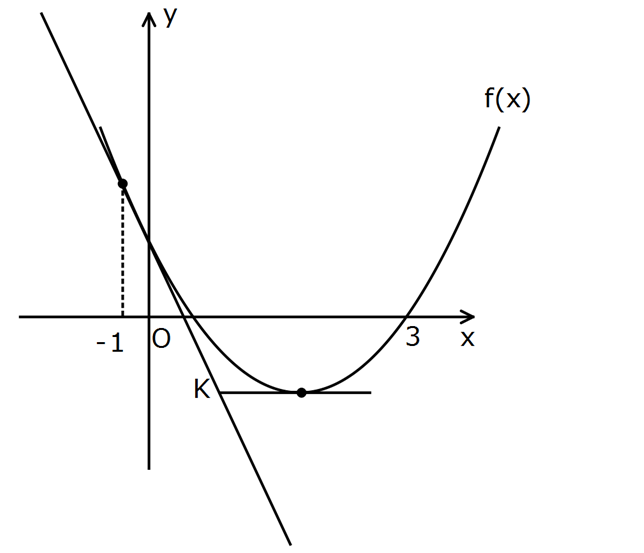
3 eğrisinin x 1 apsisli noktasındaki teğeti eğriyi bir başka B noktasın da kest f(x) iğ x ine gö re, B noktasının apsisi kaçtır? A) 2 B) 1 C) 1 D) 2 E) 3 www.matematikkolay.net 2 2 3 3 Teğetin eğim denklemi f ‘(x) 3x dir. x 1 noktasında f ‘(1) 3.1 3 tür. x 1 için f( : x) x 1 Çözüm 3 1 dir. 1,1 noktasından geçen ve eğimi 3 olan doğrunun denklemi: y 1 3 x 1 y 1 3x 3 y 3x 2 dir. y 3x 2 doğrusu ile y x eğrisi nerde ke 3 3 2 3 2 2 x 4x 3 2 2 2 2 2 2 sişir, bulalım. x 3x 2 x 3x 2 0 2x çıkarıp, ekleyelim. x 2x 2x 3x 2 0 x 2x x 2x 4x 2 0 x x 2x 1 2 x 2x 1 0 x 2x 1 x 2 0 x 1 x 2 0 Kökler x 1 ve x 2 dir. x 1’i biliyorduk zaten. B noktasın ın apsisi x 2 dir. Cevap: A 158
3 f(x) x 1 eğrisine, üzerindeki x 1 apsisli nok – tasından çizilen teğet eğriyi başka bir noktada k esi – yor. Buna göre, bu nok tanın koordinatlarını bulunuz. www.matematikkolay.net 2 2 3 3 Teğetin denklemini elde etmeliyiz. Teğetin eğimi f ‘( 1) 3x 3.( 1) 3 tür. f( 1) x 1 ( 1) : 1 Çözüm 3 2 dir. ( 1, 2) noktasından geçen ve eğimi 3 olan doğru y ( 2) 3.(x ( 1)) y 2 3.(x 1) y 2 3x 3 y 3x 1 doğrusudur. Denklemleri birbirine eşitleyerek kesişim noktasını bulabiliriz. x 1 3x 1 3 3 2 2 x 2 x 3x 2 0 x x 2x 2 0 x(x 1) 2(x 1) 0 x(x 1)(x 1) 2(x 1) 0 (x 1)(x.(x 1) 2) 0 (x 1)(x x 2) 0 (x 1)(x 2)(x 1) 0 Diğer x noktası x 2 dir. x 2 için y 3x 1 3.2 1 7 dur. Kesişim noktası (2, 7) bulu ruz. 31
www.matematikkolay.net 2 3 3 f(x) lnx eğrisine A(e , 6) noktasından çizilen teğet x eksenini hangi noktada keser? A) (4e , 3 3 3 3 0) B) (2e , 0) C) ( e , 0) D) ( 2e , 0) E) ( 3e , 0) 2 2 2 2 3 3 3 3 x ‘ 2x 2 f ‘ x lnx ‘ tir. x x x 2 Teğetin eğimi f ‘ e tür. e 2 Eğimi olan ve A e ,6 noktasın e : Çözüm 3 3 3 3 0 3 3 3 3 3 3 3 3 dan geçen doğrunun denklemi; 2 y 6 x e tür. e y 0 için x ne olur, bulalım. 2 y 6 x e e 2 6 x e e 6e 2 x e 3e x e 2e x buluruz. 2e , 0 noktası Cevap: D www.matematikkolay.net 165

