Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında Teğetin Eğimi, Teğetin Denklemi, Normalin Eğimi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU

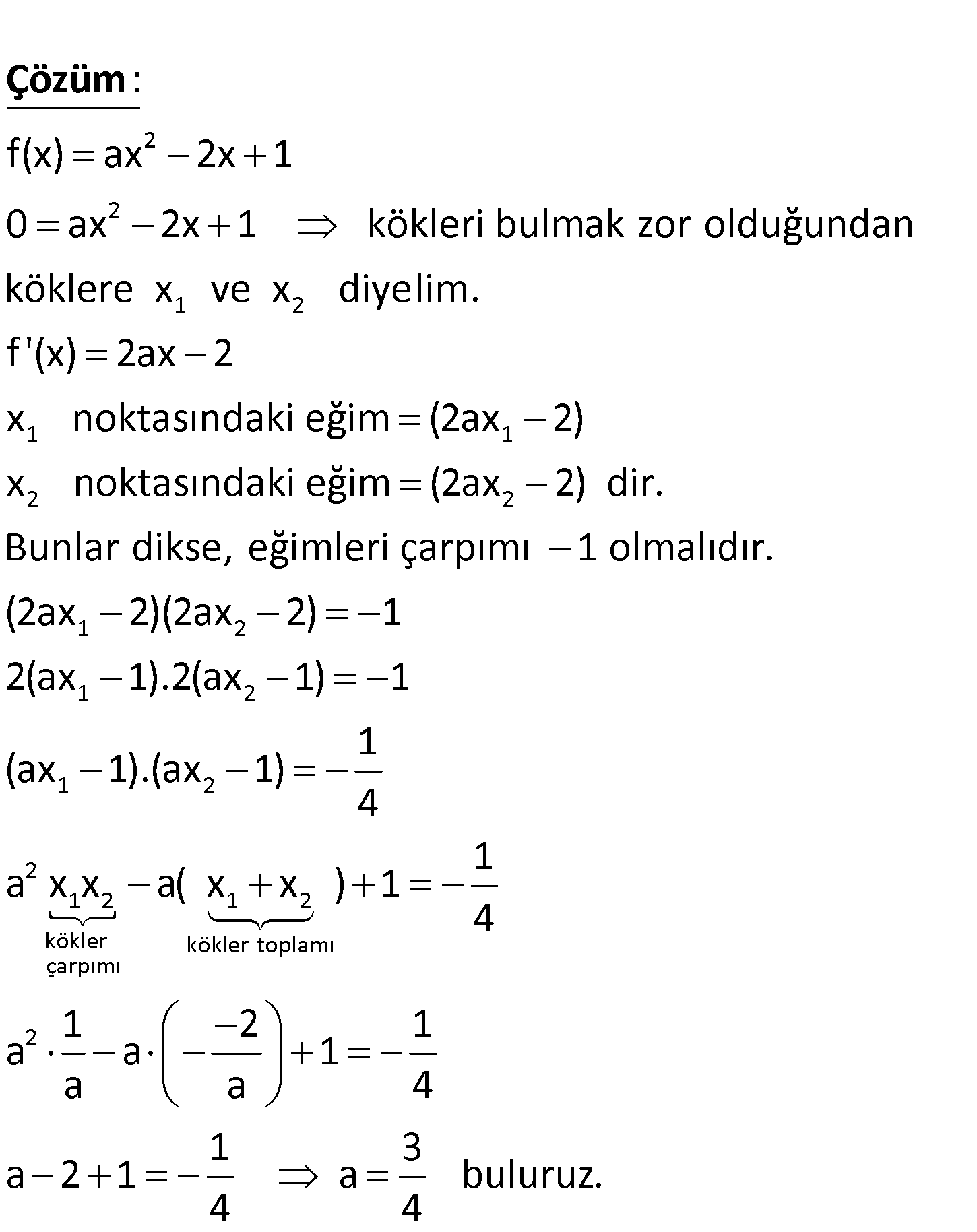
5.SORU

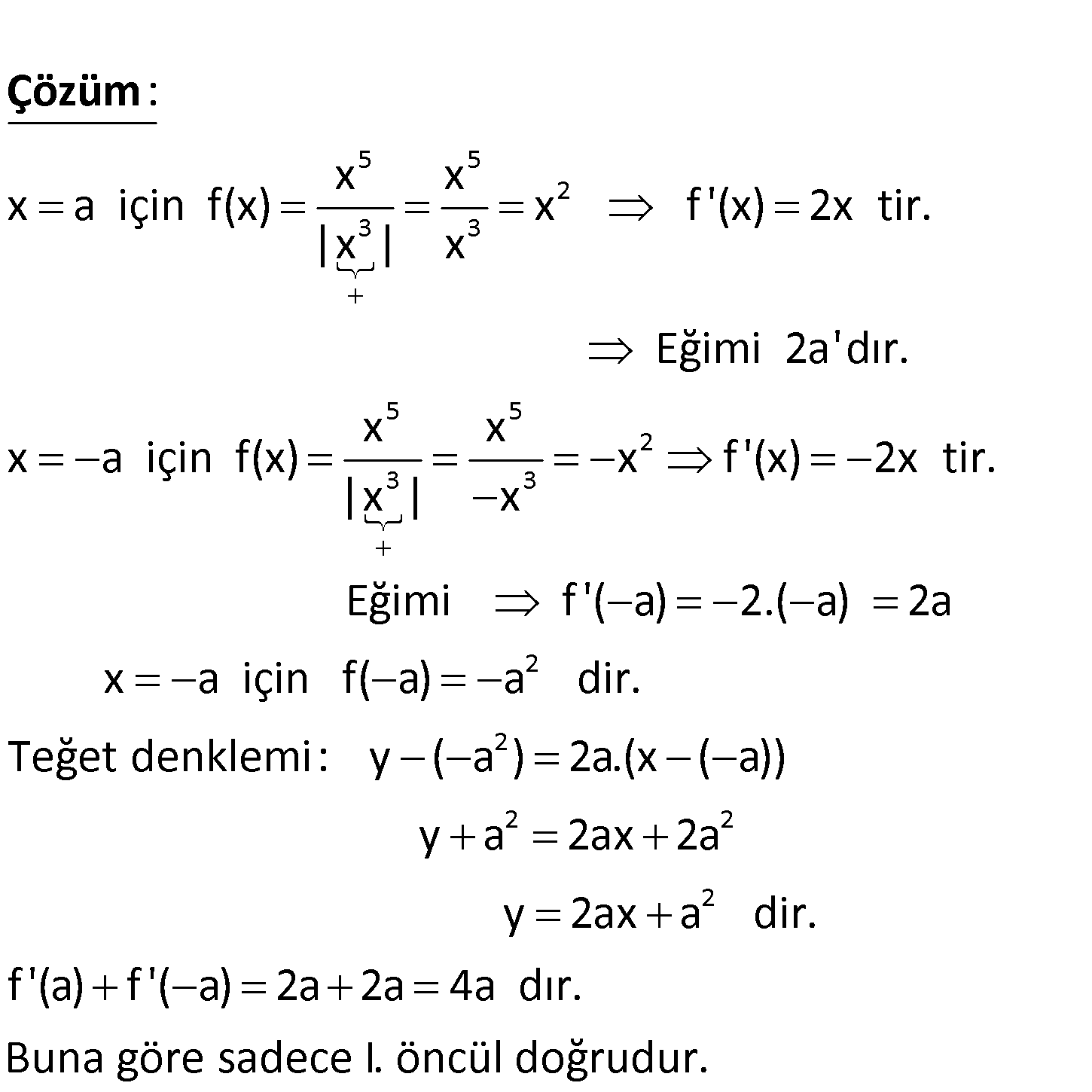
6.SORU
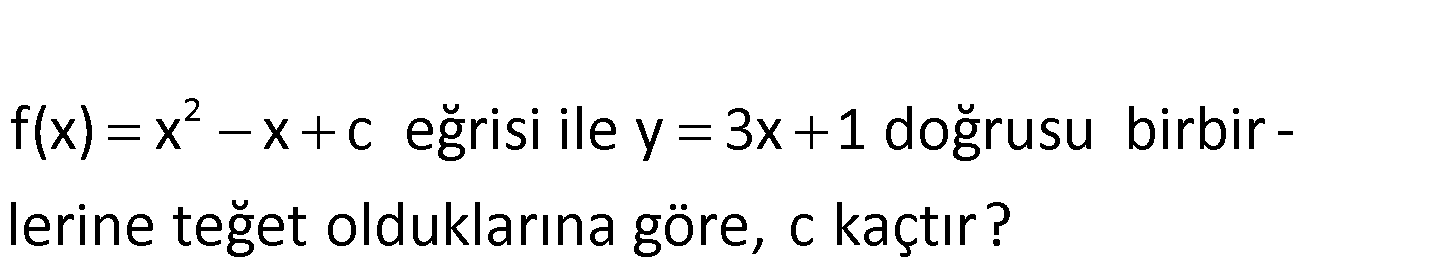

7.SORU

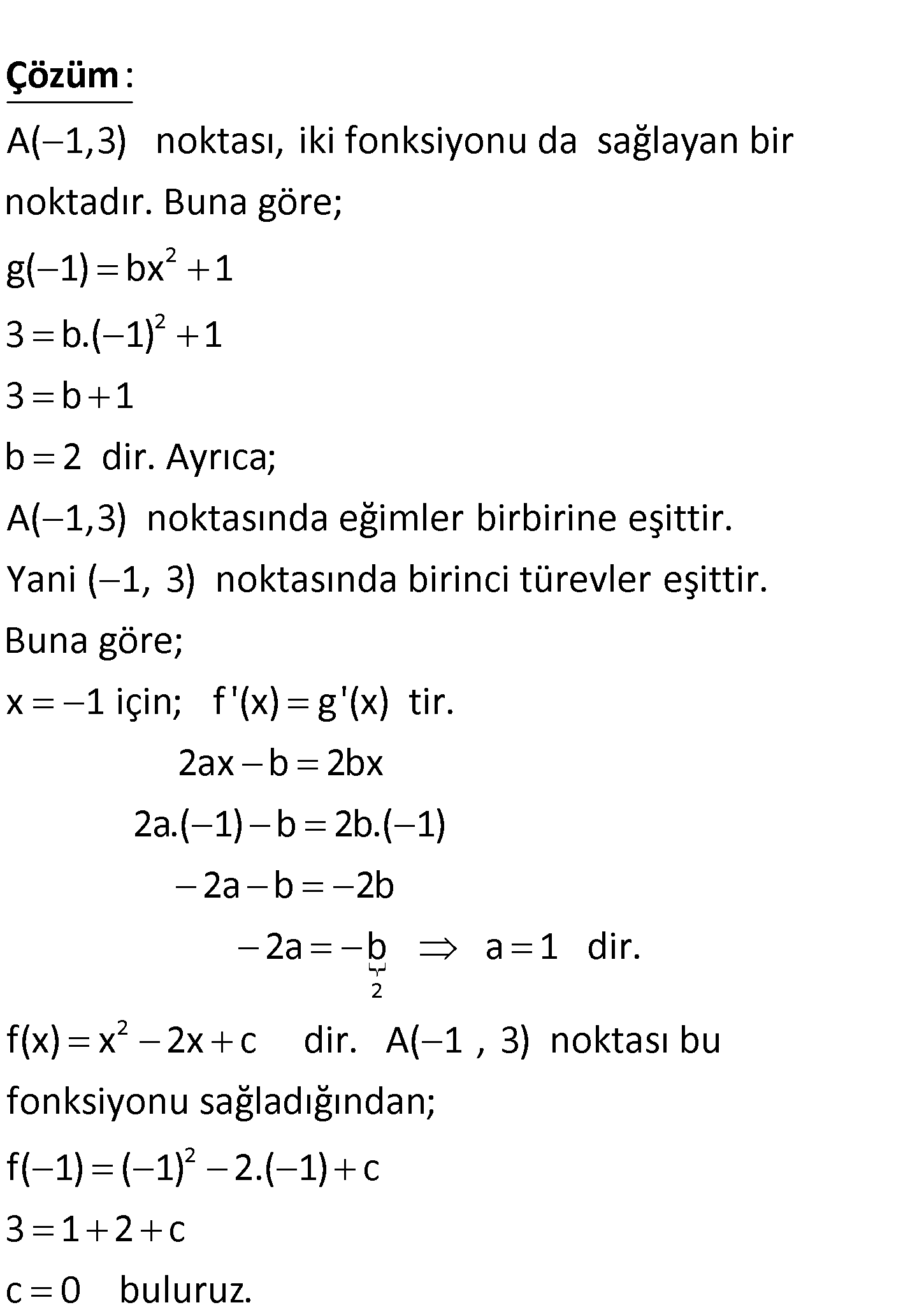
8.SORU


9.SORU
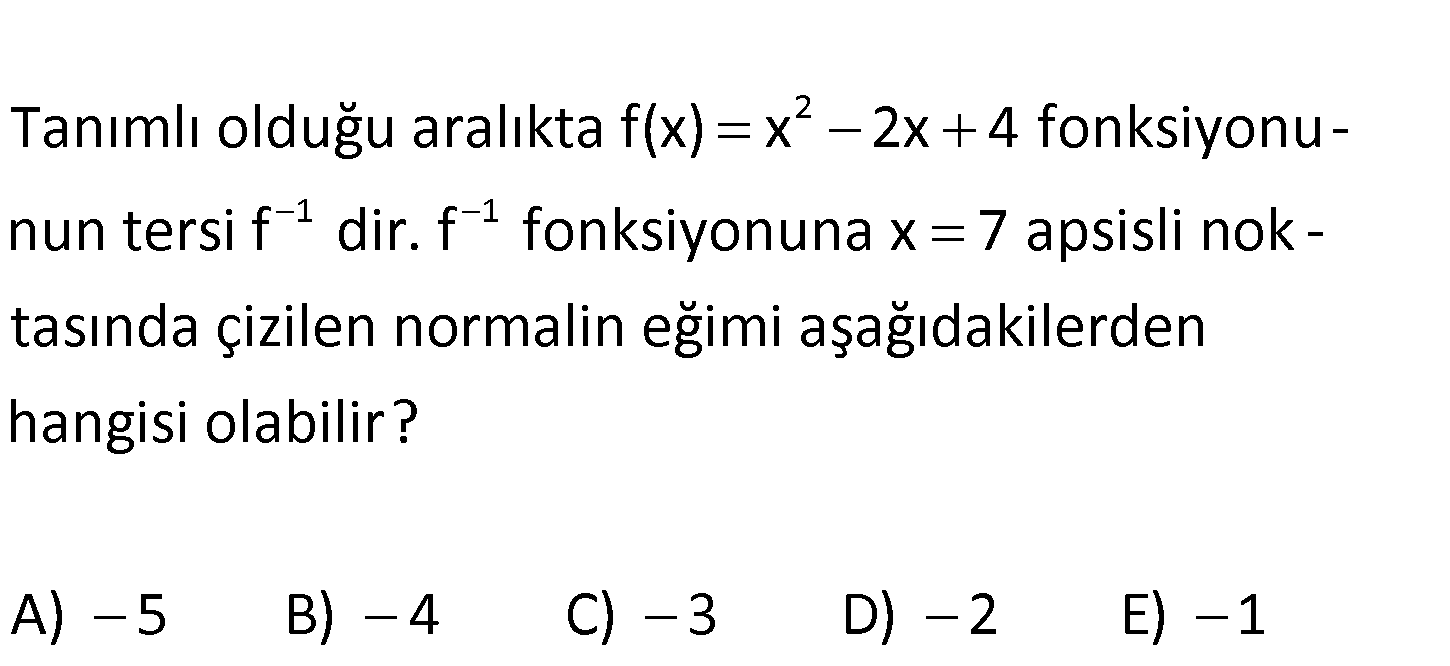

10.SORU


11.SORU

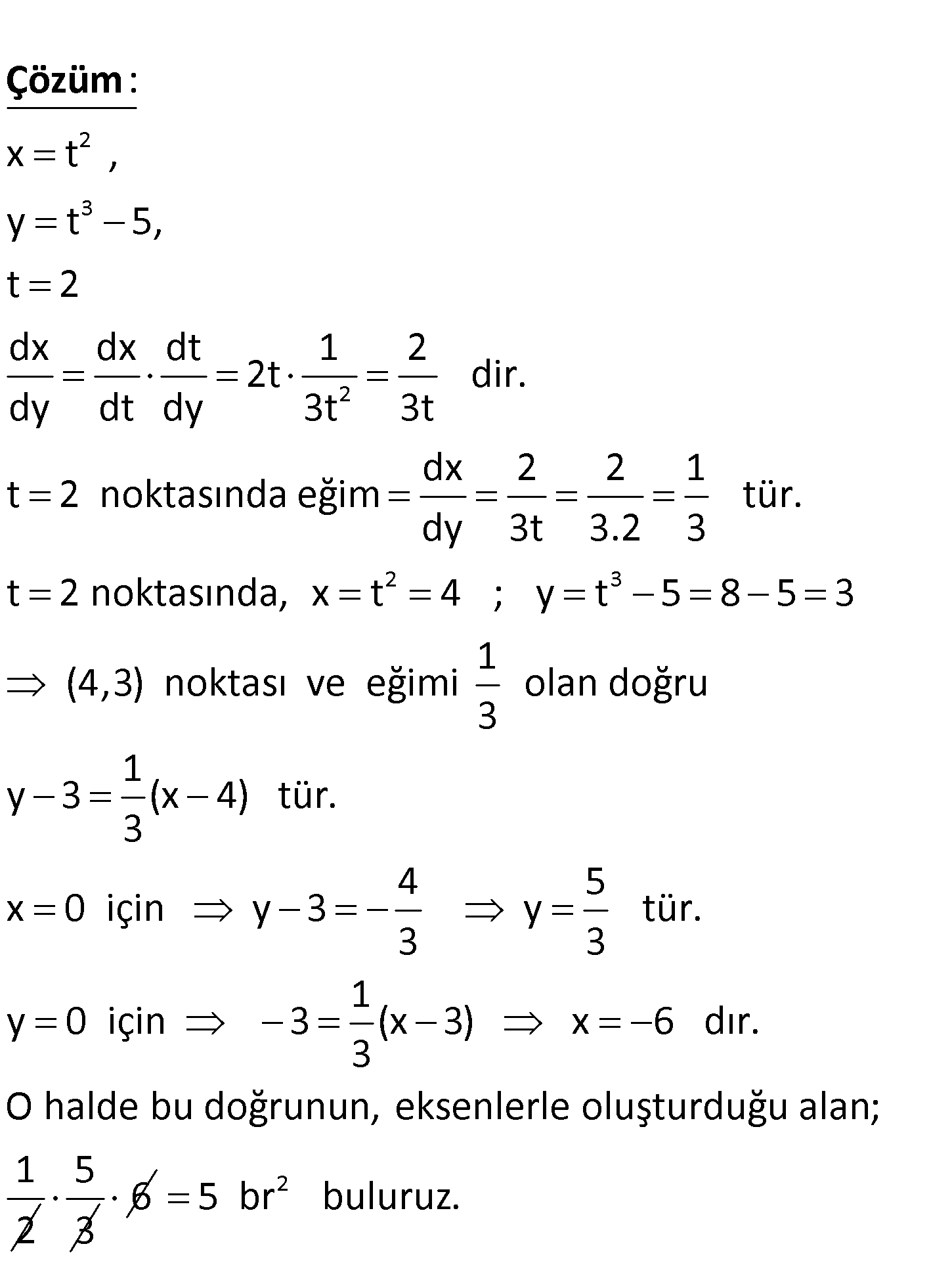
12.SORU


13.SORU
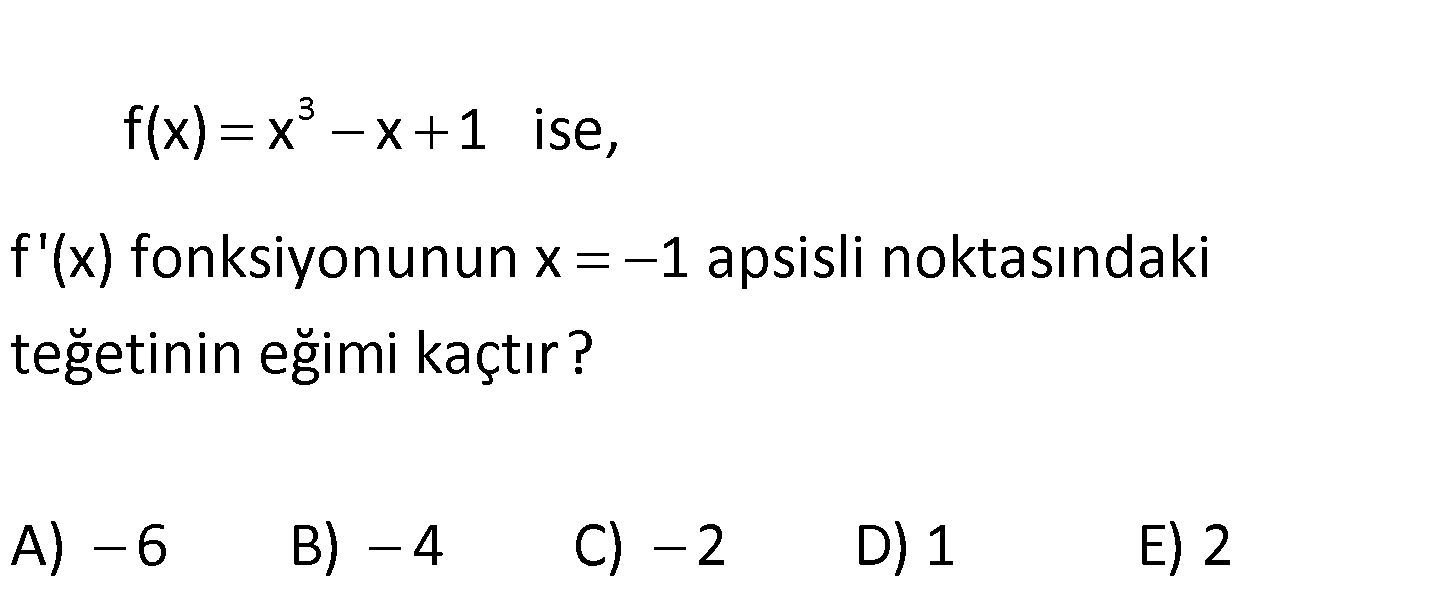

Burdan sonraki sorular, Fen Lisesi Müfredatı için geçerlidir.
14.SORU
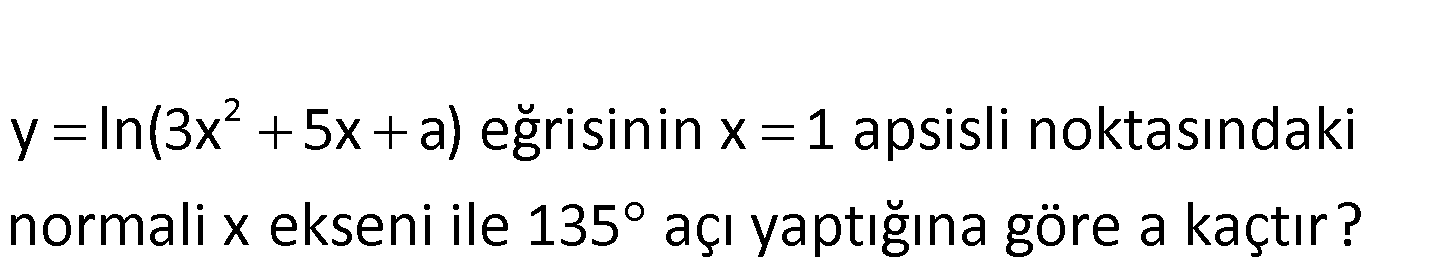

15.SORU
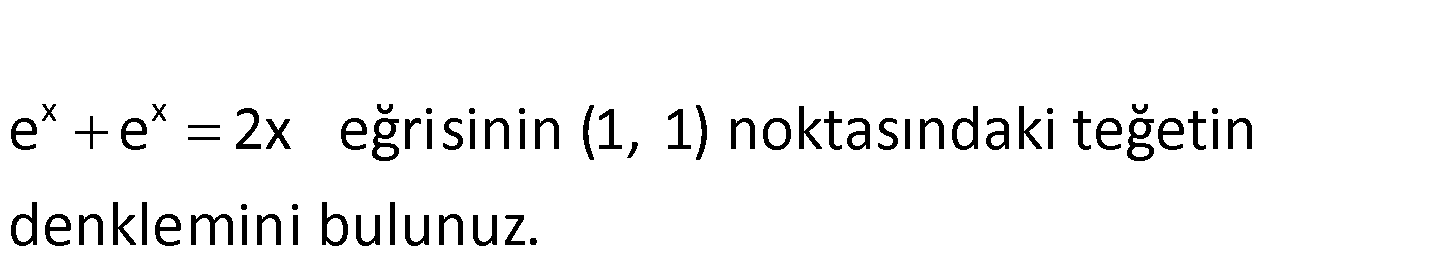

16.SORU
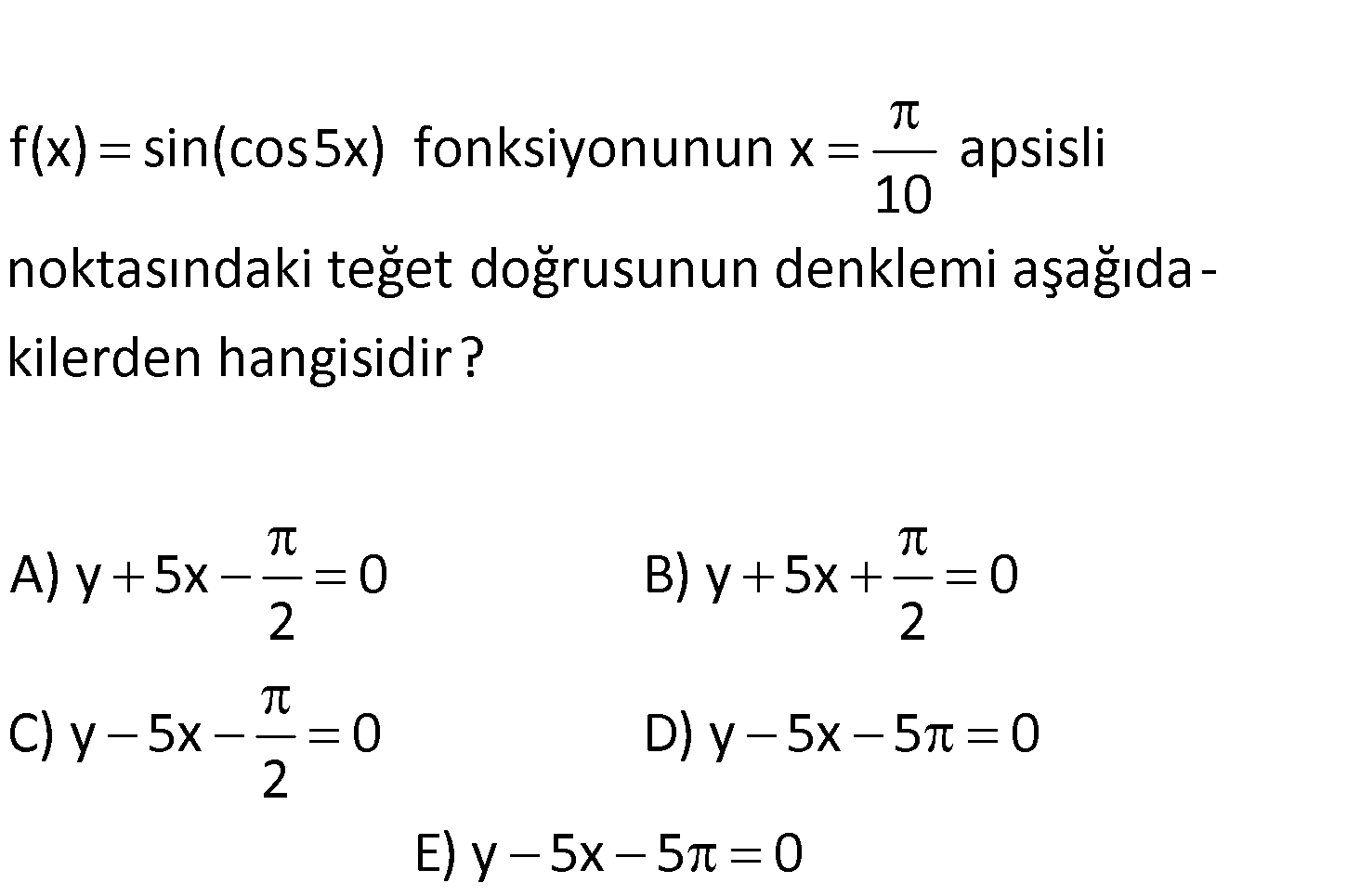
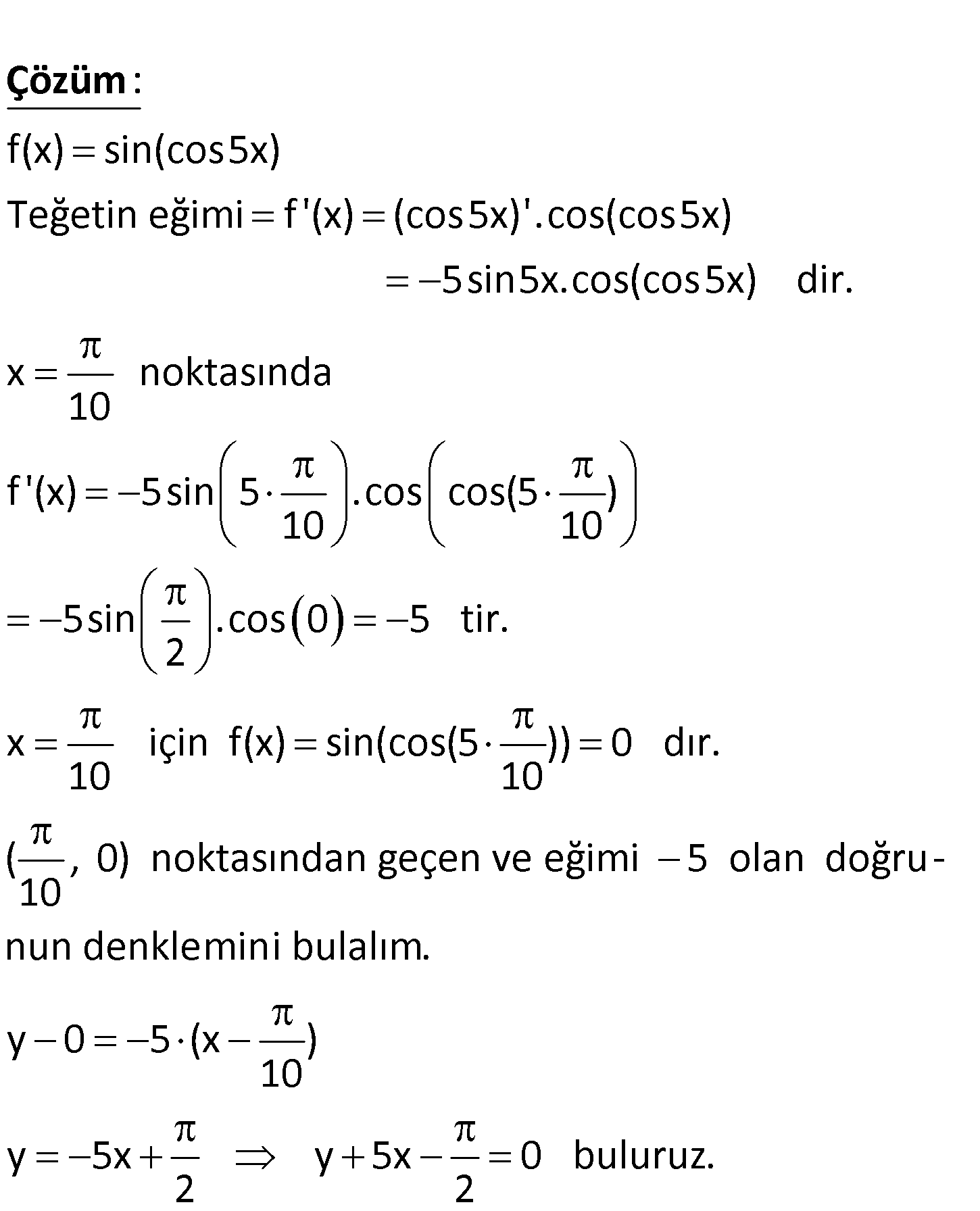
17.SORU
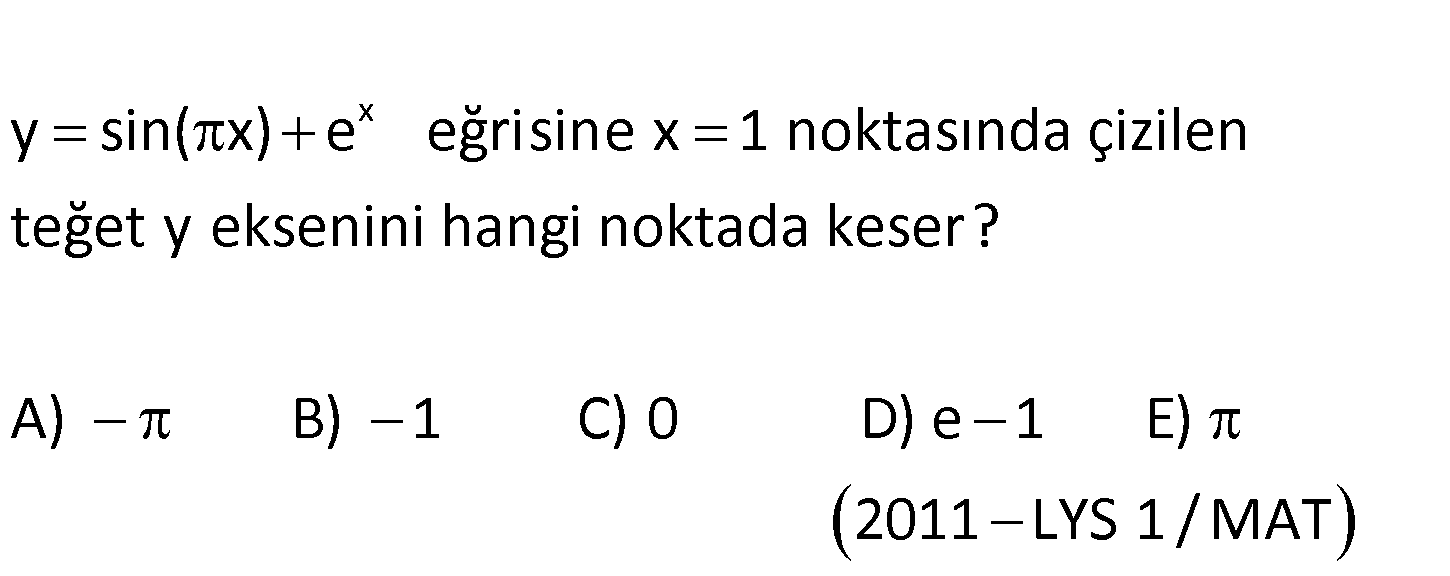

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
4 y 7x k doğrusu x y x 2 fonksiyonunun grafiğine teğet oldu- 4 ğuna göre, k kaçtır? A) 9 B) 8 C) 7 D) 8 E) 10 4 Teğet oldukları için iki fonksiyonun eğimleri eşittir. y 7x k doğrusunun eğimi 7 dir. x y : x 4 Çözüm 3 3 3 3 4 4 2 fonkisyonun türevi eğimi verir. 4x y’ 1 4 y’ x 1 7 x 1 8 x x 2 buluruz. x 2 x 2 için, y x 2 y 2 2 4 tür. 4 4 (2,4) noktası aynı zamanda y 7x k doğrusu üstünde 4 7.2 k 4 14 k k 10 buluruz. Doğru C evap: E şıkkı www.matematikkolay.net 7
www.matematikkolay.net 3 f(x) x 2x 1 fonksiyonunun (2, 9) noktasında teğet olan teğet doğrusunun denklemini bu l unuz? 2 2 f(x) fonksiyonun türevi bize teğetin eğimini verir. f ‘(x) 3x x f ‘(2) 3.2 2 12 2 14 : bu Çözüm luruz. (2,9) noktasından geçen ve eğimi 14 olan doğrunun denklemi: y 9 14(x 2) y 9 14x 28 y 14x 19 buluruz. 15
2 f(x) 2x x 1 fonksiyonunun apsisi x 2 nok – tasından geçen teğetin eğim ini b ulu ? nuz 2 İlk türev, bize eğim denklemini verir. f(x) 2x x 1 f ‘(x) 4x 1 f ‘( 2) 4.( 2) 1 8 1 : Çözüm 7 buluruz. 19
2 f(x) ax 2x 1 eğrisinin x eksenini kestiği noktalardan eğriye çizi – len teğetler birbirine di k olduğuna göre, a nın değeri kaçtır? 1 1 1 3 5 A) B) C) D) E) 4 3 2 4 4 2 2 1 2 f(x) ax 2x 1 0 ax 2x 1 kökleri bulmak zor olduğundan köklere x ve x diyelim. f ‘ x : ( Çözüm 1 1 2 2 1 2 1 2 1 2 2 1 2 kökler çarpımı ) 2ax 2 x noktasındaki eğim (2ax 2) x noktasındaki eğim (2ax 2) dir. Bunlar dikse, eğimleri çarpımı 1 olmalıdır. (2ax 2)(2ax 2) 1 2(ax 1).2(ax 1) 1 1 (ax 1).(ax 1) 4 a x x a( x 1 2 kökler toplamı 2 1 x ) 1 4 1 2 1 a a 1 a a 4 1 3 a 2 1 a buluruz. 4 4 www.matematikkolay.net 70
www.matematikkolay.net 5 3 x a 0 olmak üzere, f(x) fonksiyonu için x I. x a apsisli noktasındaki teğetinin eğimi 2a dır. II 2 . x a apsisli noktasındaki teğet doğrusunun denklemi y 2ax a dir. III. f ‘(a) f ‘( a) 0 ifadelerinden hangileri doğrudur? A) Yalnız I B) Yalnız II C) Yalnız III D) I ve II E) II ve III 5 5 2 3 3 x x x a için f(x) x f ‘(x) 2x tir. |x | x : Çözüm 5 5 2 3 3 2 Eğimi 2a’dır. x x x a için f(x) x f ‘(x) 2x tir. |x | x Eğimi f ‘( a) 2.( a) 2a x a için f( a) a dir. Teğet denklemi: 2 2 2 2 y ( a ) 2a.(x ( a)) y a 2ax 2a y 2ax a dir. f ‘(a) f ‘( a) 2a 2a 4a dır. Buna göre sadece I. öncül doğrudur. 25
2 f(x) x x c eğrisi ile y 3x 1 doğrusu birbir – lerine teğet olduklarına göre, c kaçtır? 2 Teğetin eğimini türev alarak bulabiliriz. y 3x 1 y’ 3 tür. f(x) x x c f ‘(x) 2 : x 1 Çözüm 2 2 dir. Bu ikisi birbirine eşit olmalıdır. 3 2x 1 4 2x x 2 dir. x 2 noktasında y 3x 1 3.2 1 7 dir. Bu değerler, eğri denklemini de sağlar. Buna göre; f(2) x x c 7 2 2 c 7 2 c c 5 buluruz. 27
2 2 f(x) ax bx c g(x) bx 1 fonksiyonlarının grafikleri A( 1, 3) noktasında bir – b irlerine teğet olduklarına göre, c kaçtır? www.matematikkolay.net 2 2 A( 1,3) noktası, iki fonksiyonu da sağlayan bir noktadır. Buna göre; g( 1) bx 1 3 b.( 1) : Çözüm 1 3 b 1 b 2 dir. Ayrıca; A( 1,3) noktasında eğimler birbirine eşittir. Yani ( 1, 3) noktasında birinci türevler eşittir. Buna göre; x 1 için; f ‘(x) g'(x) tir. 2ax b 2bx 2 2 2 2a.( 1) b 2b.( 1) 2a b 2b 2a b a 1 dir. f(x) x 2x c dir. A( 1 , 3) noktası bu fonksiyonu sağladığından; f( 1) ( 1) 2.( 1) c 3 1 2 c c 0 buluruz. 30
2 f(x) x x 2 fonksiyonunun x eksenini kestiği noktalarda çizilen teğetlerinin eğimleri çarpım ı kaçtır? A) 5 B) 6 C) 7 D) 8 E) 9 www.matematikkolay.net 2 x x 2 0 (x 2)(x 1) 0 x ekseni x 2 ve 1 noktasında kesiliyor. f ‘(x) 2x 1 dir. f ‘(2) 2.2 1 : Çözüm 3 f ‘( 1) 2.( 1) 1 3 Çarpımları 3.( 3) 9 buluruz. 37
2 1 1 Tanımlı olduğu aralıkta f(x) x 2x 4 fonksiyonunun tersi f dir. f fonksiyonuna x 7 apsisli no k – tasında çizilen normalin eğimi aşağıdakilerden hangisi olabilir? A) 5 B) 4 C) 3 D) 2 E) 1 www.matematikkolay.net 2 2 x 2x 4 7 ( 7 yapan x değerini bulalım) x 2x 3 0 (x 3)(x 1) 0 x 3 veya : x 1 f ‘(x) Çözüm 2 1 1 (x 2x 4)’ 2x 2 1 1 1 (f )'(7) veya f ‘(3) 2.3 2 4 1 1 1 (f )'(7) tür. f ‘( 1) 2.( 1) 2 4 Bunlar, teğetin eğimidir. Normalin eğimi ise 4 veya 4 tür. 38
2 f(x) x ax 3 fonksiyonuna üzerindeki x 1 apsisli noktadan çizilen teğet x ekseniyle pozitif yönde 45 lik açı yaptığına göre, a kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 www.matematikkolay.net Teğetin eğimi tan45 1 dir. f ‘( 1) 1 olmalıdır. 2x a 1 2 a 1 a 3 tür. : Çözüm 79
2 3 x t ve y t 5 eğrisine ait t 2 noktasından çizilen teğetin eksenlerle oluşturduğu kap 2 alı bölg enin alanı kaç br dir? 2 3 2 x t , y t 5, t 2 dx dx dt 1 2 2t dir. dy dt dy 3t 3t dx 2 2 1 t 2 noktasında : eğim dy 3t 3.2 3 Çözüm 2 3 tür. t 2 noktasında, x t 4 ; y t 5 8 5 3 1 (4,3) noktası ve eğimi olan doğru 3 1 y 3 (x 4) tür. 3 4 5 x 0 için y 3 y tür. 3 3 1 y 0 için 3 (x 3) x 6 dır. 3 O halde bu doğr unun, eksenlerle oluşturduğu alan; 1 2 5 3 6 2 5 br buluruz. 106
2 y x 4 eğrisine A( 1, 2) noktasından çizilen teğetlerin değme noktalarının apsisleri toplamı kaçtır ? A) 2 B) 1 C) 0 D) 1 E) 2 www.matematikkolay.net 2 Bu teğetlerin eğimi y ‘ 2x tir. Teğetlerin bu eğriye değdiği noktayı (x, x 4) : olarak ifade e Çözüm 2 2 2 2 2 2 debiliriz. (x, x 4) ile A( 1, 2) arasındaki eğim 2x e eşit olmalıdır. x 4 2 2x x 1 x 2 2x x 1 x 2 2x 2x 0 x 2x 2 2 Kökler toplamı 2 buluruz. 1 138
www.matematikkolay.net 3 f ‘(x) fonksiyonunun x 1 apsisli noktasındaki teğeti f(x) x x 1 nin eğimi ka i çtır? A) se, 6 B) 4 C) 2 D) 1 E) 2 3 2 f x x x 1 f ‘ x 3x 1 dir. Soruda f ‘ x in teğeti soruluyor. f x değil Bu sebeple tekrar türev ala : Çözüm 2 cağız. 3x 1 ‘ 6x tir. x 1 için teğetin eğimi 6x 6. 1 6 buluruz. 159
2 y ln(3x 5x a) eğrisinin x 1 apsisli noktasındaki normali x ekseni ile 135 açı yaptığına göre a ka çtır? T x ekseni ile 135 açı yapıyorsa; normalin eğimi tan135 1 dir. teğetin eğimi ise m .( ) 1 : 1 Çözüm T 2 m 1 dir. 6x 5 6 5 y’ 1 3x 5x a 3 5 a 11 1 a 3 buluruz. 8:00 AM 59
x x e e 2x eğrisinin (1, 1) noktasındaki teğetin d enklemini bul z unu . www.matematikkolay.net x x x x İlk türev, bize teğetin eğimini verir. e e 2x ‘ e e 2 x 1 için e e 2 2e 2 dir. Eğimi 2e : Çözüm 1 1 2 olan ve (1,1) noktasından geçen teğetin denklemi; y – y m(x x ) y 1 (2e 2)(x 1) y 1 2ex 2e 2x 2 y x(2e 2) 2e 3 buluruz. 58
f(x) sin(cos5x) fonksiyonunun x apsisli 10 noktasındaki teğet doğrusunun denklemi aşağıda – kil de er n hangisidir? A) y 5x 0 B) y 5x 0 2 2 C) y 5x 0 D) y 5x 5 0 2 E) y 5x 5 0 www.matematikkolay.net f(x) sin(cos5x) Teğetin eğimi f ‘(x) (cos 5x)’.cos(cos 5x) : Çözüm 5sin5x.cos(cos5x) dir. x noktasında 10 f ‘(x) 5sin 5 .cos cos(5 ) 10 10 5sin .cos 0 5 tir. 2 x için f(x) sin(cos(5 )) 0 dır. 10 10 ( , 0) noktasından geçen ve eğimi 5 10 olan doğru – nun denklemini bulalım. y 0 5 (x ) 10 y 5x y 5x 0 buluruz. 2 2 23
x y sin( x) e eğrisine x 1 noktasında çizilen teğet y eksenini hangi noktada keser? A) B) 1 C) 0 D) e 1 E) 2011 LYS 1 /MAT x x x 1 için y sin( x) e sin( ) e 0 e e (1,e) noktasına eğimi bulalım. y’ cos( x) e y'(1,e c : ) Çözüm 1 os( ) e e (1,e) noktasından geçen ve eğimi e olan doğru; y e ( e )(x 1) y e x e.x e x( e) y 0 x 0 için; y buluruz. Doğru Cevap : E şıkkı 8

