Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında Koni ile ilgili Maksimum Minimum ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

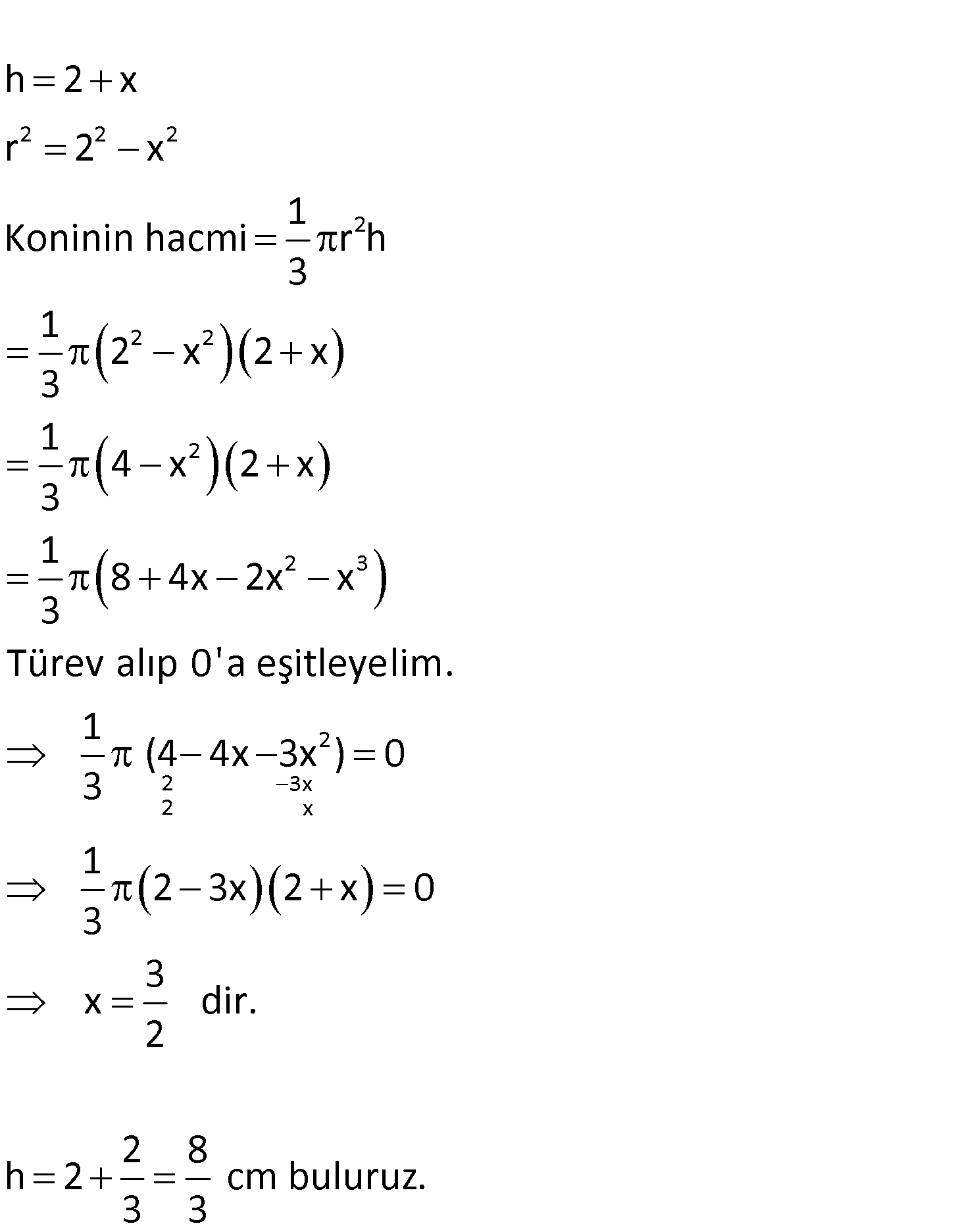
2.SORU

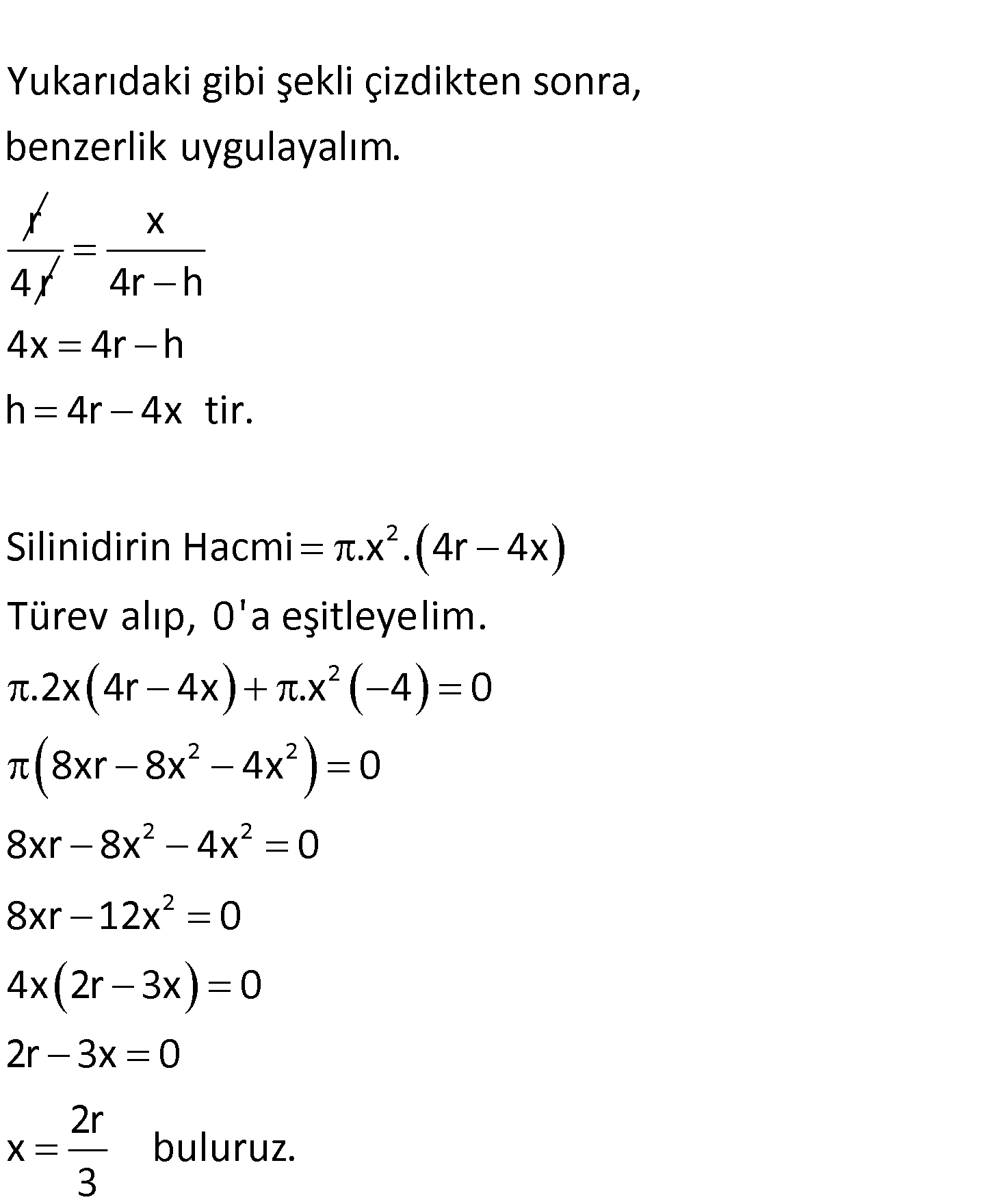
3.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
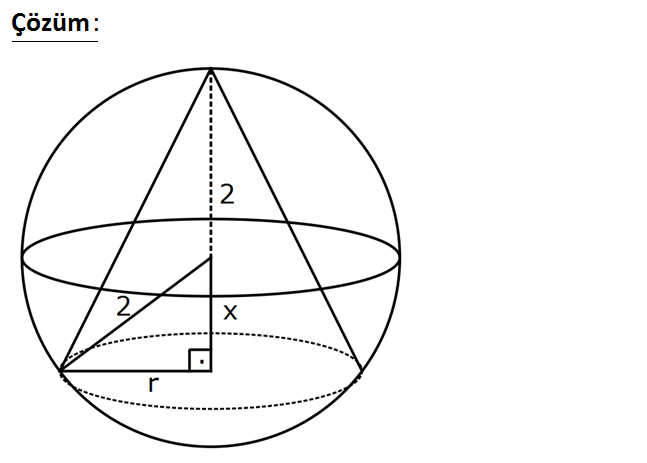
www.matematikkolay.net Yarıçapı 2 cm olan küre içine yerleştirilecek en büyük hacimli koninin yüksekliği kaç cm dir? A) 1 B 4 3 8 ) C) D) 2 E) 3 2 3 : Çözüm www.matematikkolay.net 2 2 2 2 2 2 2 2 3 h 2 x r 2 x 1 Koninin hacmi r h 3 1 2 x 2 x 3 1 4 x 2 x 3 1 8 4x 2x x 3 Türev alıp 0’a eşitleyelim. 2 2 3x 2 x 1 (4 4x 3x ) 0 3 1 2 3x 2 x 0 3 3 x dir. 2 2 8 h 2 cm buluruz. 3 3 66
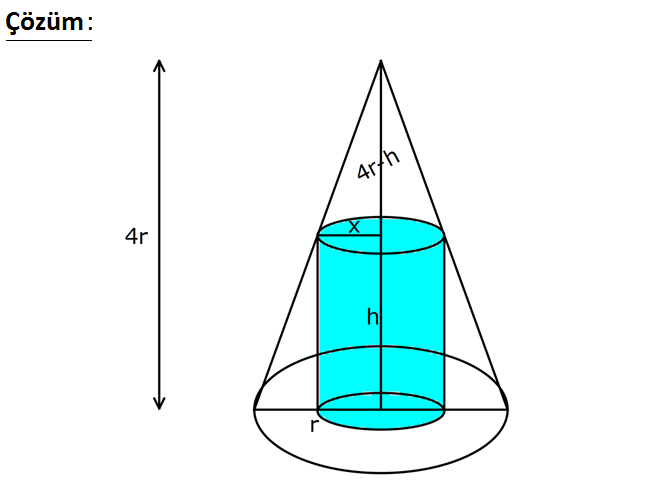
Taban yarıçapı r, yüksekliği 4r olan bir dik koninin içine en bük hacimli bir silindir yerleştirilirse bu si – lindirin yarıçapı aşağıdakilerden hangisi olur? 3r 2r r r 2r A) B) C) D) E) 4 3 3 4 5 www.matematikkolay.net : Çözüm Yukarıdaki gibi şekli çizdikten sonra, benzerlik uygulayalım. r 4 r 2 2 2 2 2 2 2 x 4r h 4x 4r h h 4r 4x tir. Silinidirin Hacmi .x . 4r 4x Türev alıp, 0’a eşitleyelim. .2x 4r 4x .x 4 0 8xr 8x 4x 0 8xr 8x 4x 0 8xr 12x 0 4x 2r 3x 0 2r 3x 0 2r x buluruz. 3 www.matematikkolay.net 183
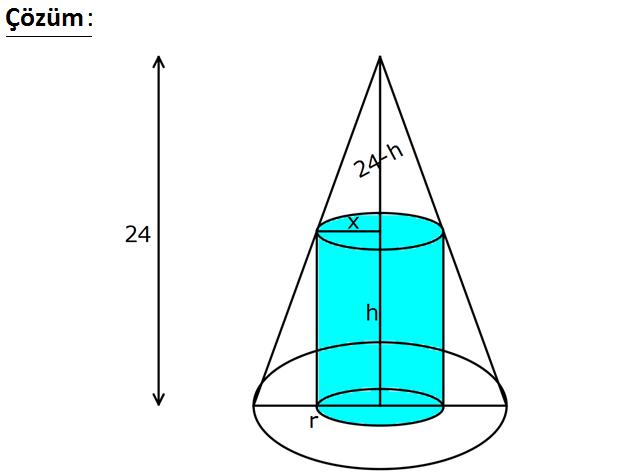
Taban çapı 24 cm ve yüksekliği 24 cm olan bir dik koni içine yerleştirilen en büyük hacimli dik silindi – rin yüksekliği kaç cm dir? A) 4 B) 6 C) 8 D) 9 E) 10 www.matematikkolay.net : Çözüm www.matematikkolay.net Koninin taban çevresi 24 cm ise 12 2 r 24 r dir. Yukarıdaki gibi şekli çizdikten sonra, benzerl 2 2 2 2 2 ik uygulayalım. r x 24 24 h 24r hr 24x 24r 24x hr 24x 24x h 24 24 24 2 x dir. r 12 Silinidirin Hacmi .x . 24 2 x Türev alıp, 0’a eşitleyelim. .2x 24 2 x .x 2 0 48x 4 x 2 x 0 48x 6 x 0 48 8 x 6 2 x 8 x 2 x 8 x dir. h 24 2 x 24 2 8 24 16 8 buluruz. 194

