Fonksiyonun Türevini Yorumlama

Fonksiyonun Türevini Yorumlama
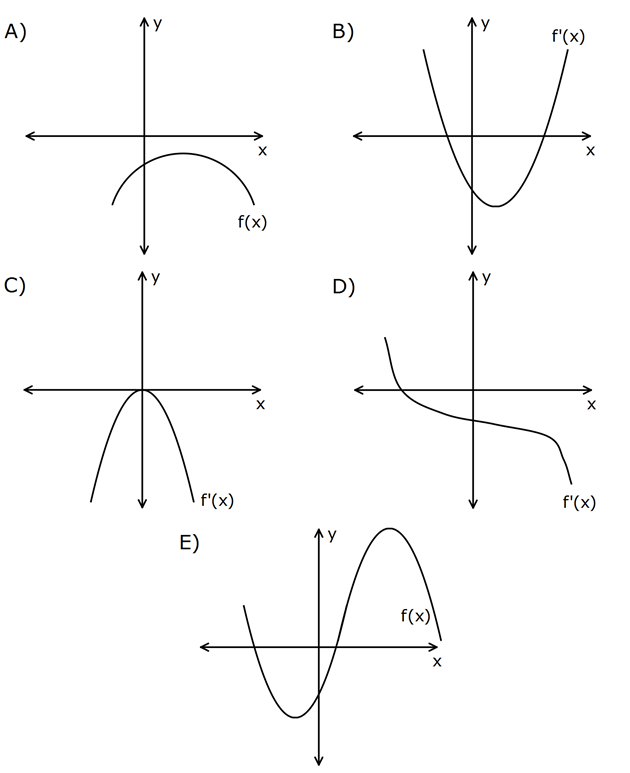
Aşağıdaki fonksiyonlardan hangisinin yerel ekstremum noktası yoktur? www.matematikkolay.net Yerel ekstremum noktası için fonksiyonun türev grafiğinde mutlaka +’dan -‘ye geçiş ya d : a tam Çözüm tersi geçiş olmalıdır. C şıkkındaki grafik pozitif alana hiç geçmemiş. Bu sebeple ekstremum noktası yoktur. A ve E şıkkında fonksiyonun direkt kendi grafikleri verilmiş. (Türevleri değil) Gözle bakıldığında yerel maksimum ve yerel minimum gibi ekstremum noktaları olduğu görülmektedir. Cevap: C şıkkı www.matematikkolay.net 6
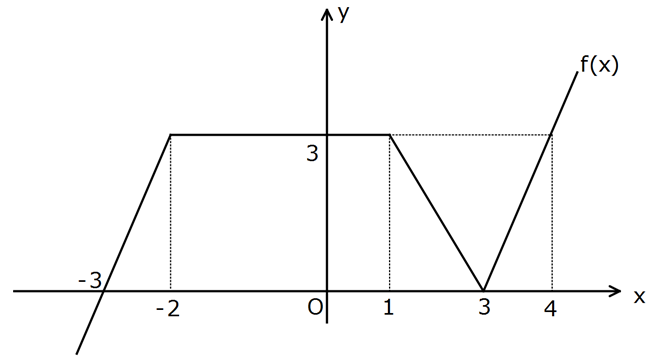
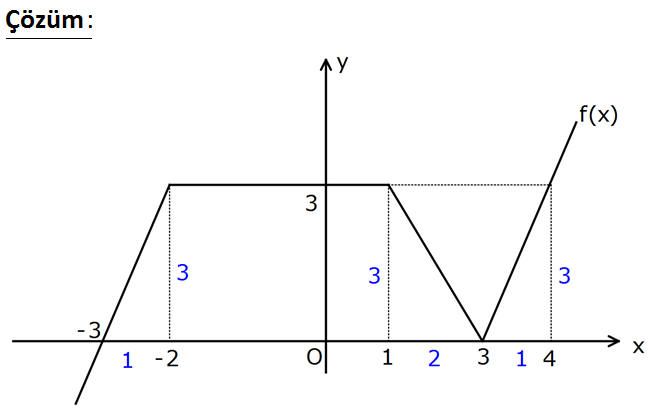
www.matematikkolay.net Şekilde f(x) fonksiyonunun grafiği verilmiştir. Buna göre, f ‘( 3) f ‘(2) f ‘( 1) işleminin sonucu kaçt ır? 1 3 A) 0 B) C) 1 D) E) 2 2 2 : Çözüm www.matematikkolay.net ı ı ı ı ı f ( 3) f (2) f ( 1) f ( 3) değeri [-3,-2] aralığındaki fonksiyonun eğimine eşittir. 3 f ( 3) 3 tür 1 ı ı ı ı ı ı . f (2) değeri [1,3] aralığındaki fonkiyonun eğimine eşittir. 3 f (2) dir. 2 f ( 1) değeri [-2,1] aralığındaki fonksiyonun eğimine eşittir.Sabit fonksiyonun eğimi 0’dır. 3 3 f ( 3) f (2) f ( 1) 3 0 bulun 2 2 ur. 176
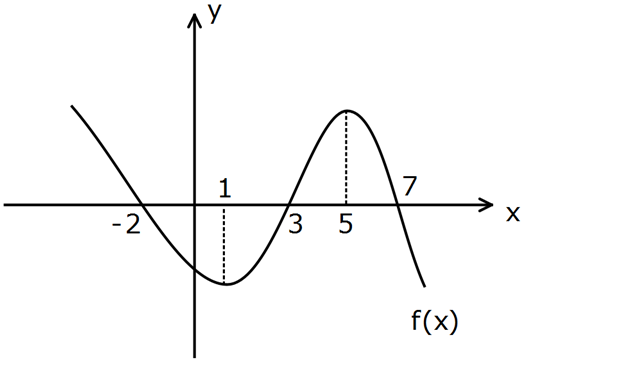
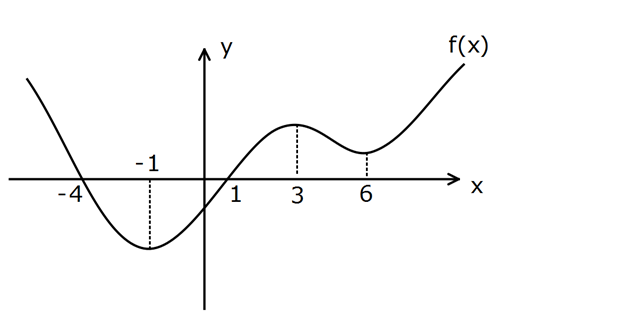
www.matematikkolay.net Yukarıda y f(x) fonksiyonunun grafiği verilmiştir. Aşağıda verilenlerden hangisi doğrudur? A) f ‘( 3) 0 B) f ‘(6) 0 C) f ‘(8) 0 D) f ‘(0) 0 E) f ‘(2) 0          f(x) ‘in kendisi grafikte verilmiştir. ,1 arasında f(x) azalıyor. A ve D şıkkı yanlış : . 1,5  Çözüm   arasında f(x) artıyor. E şıkkı yanlış. 5, arasında f(x) azalıyor. B şıkkı yanlış. Cevap: C  202
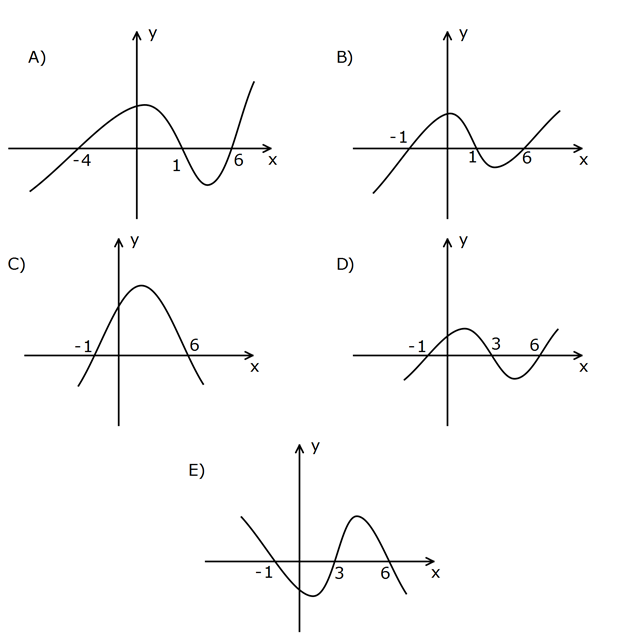
Yukarıda y f(x) fonksiyonunun grafiği verilmiştir. f ‘(x) fonksiyonunun grafiği aşağıdakilerden hangisi olabilir? www.matematikkolay.net   f(x) ‘in kendisi grafikte verilmiştir. , 1 arasında azalandır. f ‘(x) x 1’de yerel minim : um  Çözüm       vardır. f ‘( 1) 0 1,3 arasında ar tandır. f ‘(x) x 3’ te yerel maksimum vardır. f ‘(3) 0 3,6 arasında azalandır. f ‘(x) x 6’da yerel minimum vardır. f ‘(6) 0 6, arasında ar tandır. f ‘(x) Bunların gösterild  iği şık D şıkkıdır. Cevap: D 203
www.matematikkolay.net   x R 0 için tanımlı f fonksiyonu x 1 f(x) 1 x biçiminde veriliyor. Buna göre, I. f in x 1 apsisli nok  tada yerel maksimumu vardır. II. f fonksiyonu ( 1, 0) aralığında azalandır. III. y 2, f in yatay asimptot doğrusudur. ifadelerinden hangileri doğrudur? A) Yalnız I B) Yalnız II C) I ve III D) II ve III E) I, II ve III www.matematikkolay.net x 1 f(x) 1 x x 1 1 x 1 için f(x) 1 1 1 x x :  Çözüm       2 2 1 2 tir. x 1 f ‘(x) , 1 aralığında ar tandır. x x 1 1 1 x 1 için f(x) 1 1 1 tir. x x x 1 f ‘(x) 1, aralığında azalandır. x II.öncül doğrudur. x 1 n      x x x oktasında türevi olmasa da ar tanlık tan azalanlığa geçtiği için burada yerel maksimum vardır. I. öncül doğrudur. x 1 lim 1 1 0 , x x 1 x 1 lim 1 lim 1 1 1 2 x x y 0                          ve y 2 doğruları yatay asimptotlardır. III.öncül de doğrudur. 142
www.matematikkolay.net x f(x) x.e fonksiyonu için I. x (1, ) için f(x) fonksiyonu azalan fonksiyondur. II. x ( 4, 0) için    f(x) fonksiyonu ar tan fonksiyondur. 1 III. A 1, noktası f(x) fonksiyonunun yerel mak – e simum noktasıdır. ifadelerinden hangileri doğrudur? A) Yalnız I B) Yalnız II C) Yalnız III       D) II ve III E) I, II ve III www.matematikkolay.net   x x x x x f(x) xe birinci türevini incelemeliyiz. f ‘(x) 1.e x. e f ‘(x) e x.e 0’a eşitleye : Çözüm   x x x 0 0 rek esktremum noktaları bulalım. f ‘(x) e x.e 0 e 1 x 0 x 1 dir. Kritik noktamız 1 dir. x 1’den küçük olursa, örneğin 0 gibi f ‘(0) e 0.e 1 0 1 dir. Yani po   1 zitif Türev pozitif ise fonksiyon ar tandır. x 1 için f ‘(x) ar tandır. x 1 için f ‘(x) azalandır. x 1 noktasında f(x) ar tanlık tan, azalanlığa geçiyor. O halde x 1’de yerel maksimum vardı           x 1 r. 1 1 x 1 için y x.e 1.e dir. 1, noktası. e e O halde tüm öncüller doğrudur. Cevap: E       141