Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında Fonksiyonun en büyük değeri, Denklemin en büyük değeri ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU

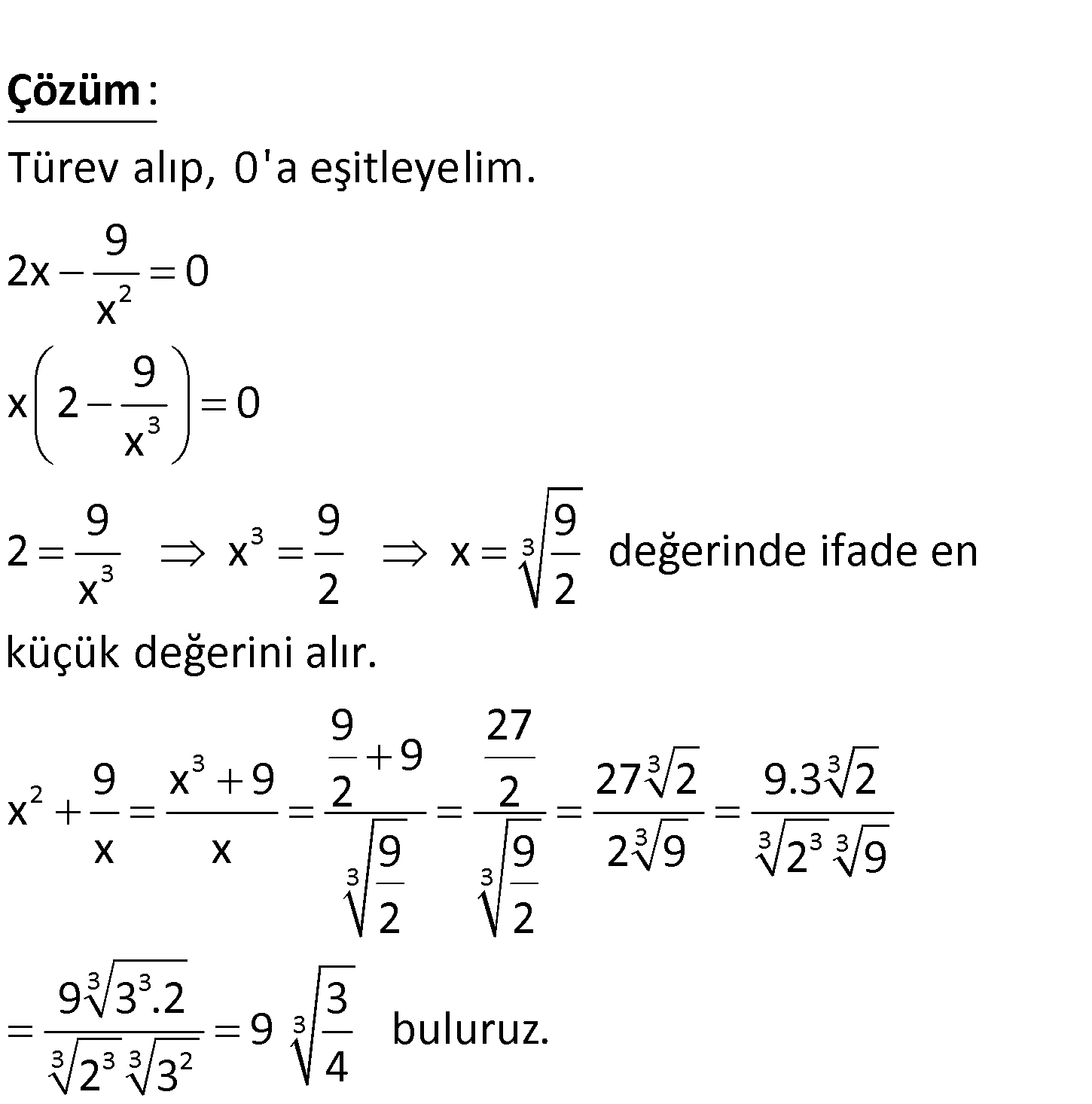
4.SORU


5.SORU

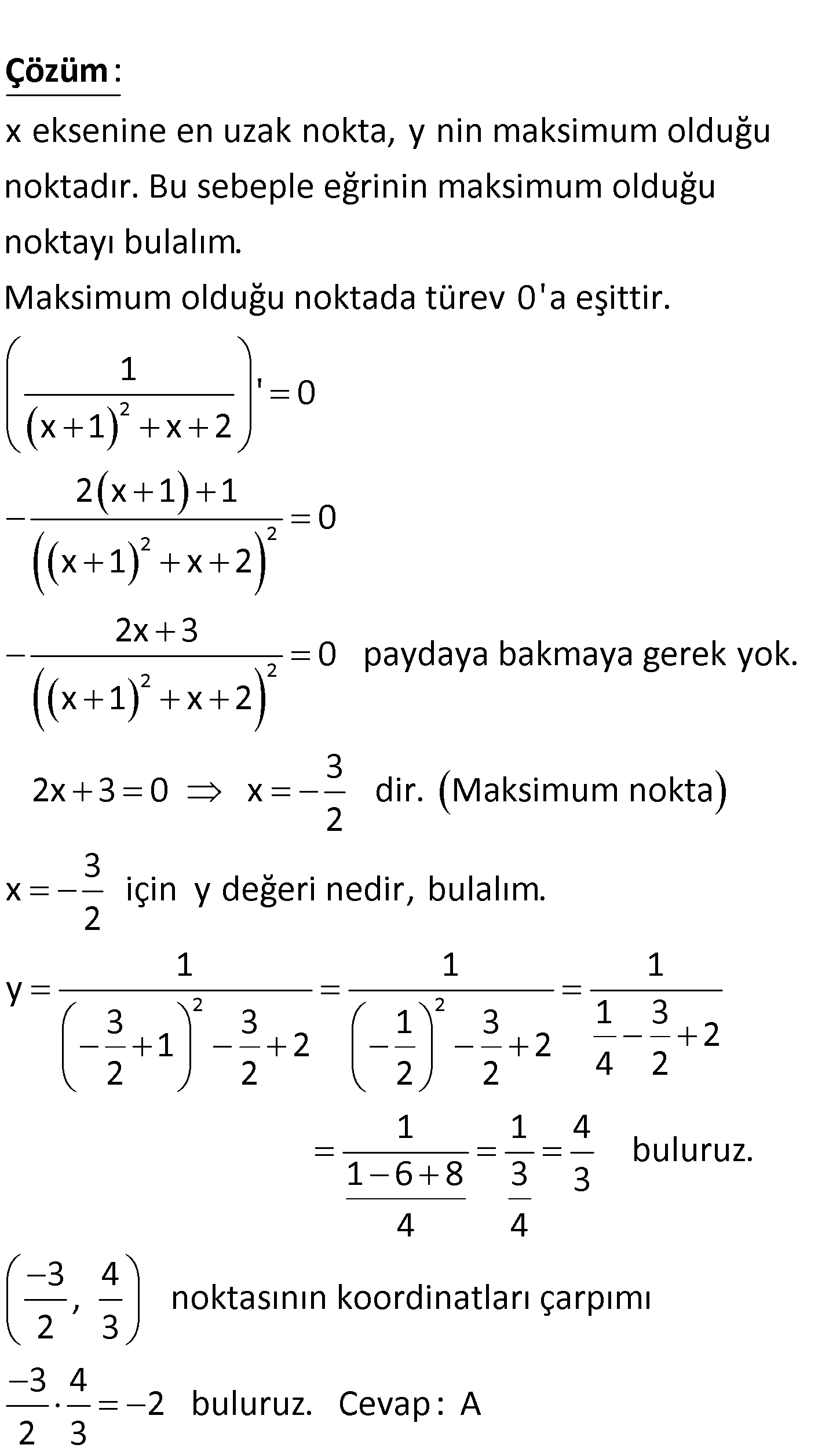
6.SORU


7.SORU


8.SORU


9.SORU


Burdan sonraki sorular, Fen Lisesi Müfredatı için geçerlidir.
10.SORU


11.SORU
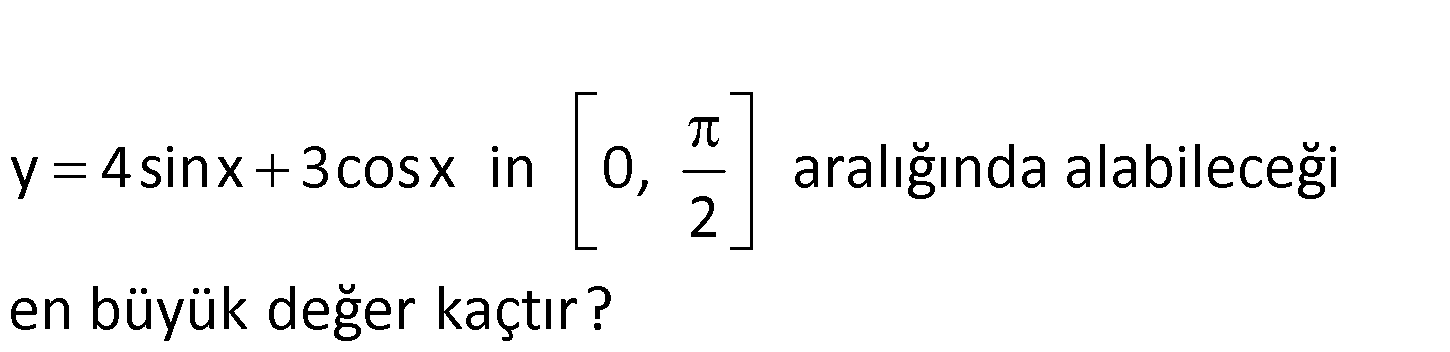

12.SORU


13.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 f(x) x 6x 1 fonksiyonunun alabileceği en büyük değ er k aç tır? www.matematikkolay.net 2 Kritik noktayı bulmak için, ilk türevini 0’a eşitleyelim. f(x) x 6x 1 f ‘(x) 2x : 6 0 Çözüm 2 2 2x 6 0 2x 6 x 3 tür. x 3 noktasında f(x)’in değerini bulalım. f(3) x 6x 1 3 6.3 1 9 18 1 10 buluruz. (En büyük değeridir) 18
2 x reel sayısı için, x x 4 farkının en küçük değeri kaçtır? www.matematikkolay.net Türev alıp, 0’a eşitleyelim. 1 1 1 2x 0 2x x dir. 4 4 8 1 x ‘de en küçük değerini alır. : 8 x Çözüm 2 -2 1 x 1 8 1 1 1 2 1 buluruz. 4 64 4 64 32 64 64 96
2 x R olmak üzere, 9 x ifadesinin en küçük değerini bulunuz. x www.matematikkolay.net 2 3 3 3 3 Türev alıp, 0’a eşitleyelim. 9 2x 0 x 9 x 2 0 x 9 9 9 2 x x değerinde ifade : e x 2 2 Çözüm 3 3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 2 n küçük değerini alır. 9 27 9 9 x 9 2 2 27 2 9.3 2 x x x 9 9 2 9 2 9 2 2 9 3 .2 3 9 buluruz. 2 3 4 110
3 2 f(x) x 3x 24x 4 fonksiyonunun grafiğine herhangi bir noktada çizi – len teğetin eğiminin d eğeri en çok kaç olur? www.matematikkolay.net Teğetin eğimi 1. türevden bulunur.Eğimin en büyük değeri için 1. türevin de türevi alın : arak Çözüm 3 2 ı 2 ıı ı 2 ı 0’a eşitlenmeli.Yani ikinci türev alınmalı f x x 3x 24x 4 f x 3x 6x 24 f x 6x 6 6x 6 0 x 1 dir. f 1 3.1 6.1 24 f 1 27 bulunur. 145
2 1 y (x 1) (x 2) eğrisinin x eksenine en uzak noktasının koordinat – ları çarpımı kaçtır? 3 A) 2 B) 1 C) 0 D) E) 2 2 www.matematikkolay.net x eksenine en uzak nokta, y nin maksimum olduğu noktadır. Bu sebeple eğrinin maksimum ol : duğu n Çözüm 2 2 2 2 2 oktayı bulalım. Maksimum olduğu noktada türev 0’a eşittir. 1 ‘ 0 x 1 x 2 2 x 1 1 0 x 1 x 2 2x 3 0 paydaya bakmaya gerek yok. x 1 x 2 3 2x 3 0 x dir. Maksimum nokta 2 3 x için y değer 2 2 2 i nedir, bulalım. 1 1 1 y 3 3 1 3 1 3 1 2 2 2 2 2 2 2 4 2 1 1 4 buluruz. 1 6 8 3 3 4 4 3 4 , noktasının koordinatları çarpımı 2 3 3 4 2 buluruz. Ce 2 3 vap: A www.matematikkolay.net 161
2 3 Toplamları 5 olan x ve y gibi iki pozitif sayı için x .y ün maksimum değeri kaçtır? A) 108 B) 100 C) 86 D) 64 E) 32 www.matematikkolay.net 2 3 2 3 x y 5 ise y 5 x tir. Buna göre; x .y x . 5 x tür. Maksimum değerini bulmak için türev a : Çözüm 2 3 3 22 3 2 2 2 2 2 Çift katlı 2 lıp, 0’a eşitleyelim. x . 5 x ‘ 0 2x. 5 x 3. 1 5 x .x 0 2x. 5 x 3 5 x .x 0 x 5 x 2 5 x 3x 0 x 5 x 10 2x 3x 0 x 5 x 10 5x 0 Kökler x 0 , x 2 ve x 5 tir. x 5 x 10 5x açılımında en büyük dereceli terim 0 2 5 Max 2 3 2 3 in işareti dir. İşaret tablosunda sağdan ile başlayarak yapalım. | | || x 2 için maksimum değerini alır. Cevap x . 5 x 2 5 2 4.27 108 buluruz. 177
2 x, y R olmak üzere, x y 12 olduğuna göre, y .x ifadesinin en büyük değerini alması için x kaç ol malıdır? A) 12 B) 8 C) 6 D) 4 E) 2 2 2 x y 12 ise y 12 x tir. O halde; y x 12 x x tir. Türev alıp, 0’a eşitleyelim. 2 12 x 1 x 1 x : 2 Çözüm 2 2 .1 0 12 x 2 12 xx 12 x 2x 12 3x x 4 buluruz. www.matematikkolay.net 186
www.matematikkolay.net Çarpımları 16 olan iki pozitif reel sayının toplamları – nın en küçük değeri kaçtır? A) 6 B) 8 C) 9 D) 16 E) 17 2 16 x.y 16 ise y tir. x 16 Toplamları x olur. x Türevini 0’a eşitleyelim. : 16 x ‘ 0 x 16 1 x Çözüm 2 0 x 16 x 4 tür. 16 O halde toplamları 4 4 4 8 buluruz. 4 196
www.matematikkolay.net Üç pozitif sayının toplamı 13 tür. Birinci sayı ikinci sayının 3 katı olduğuna göre, üç sayının çarpımının alabileceği en büyük değer için üçüncü sayı kaç olur? 26 13 13 A) 9 B) 5 C) D) E) 3 3 2 2 2 3 Bu üç sayı 3x, x ve 13 4x şeklindedir. Çarpımları x.3x. 13 4x tir. 3x 13 4x 39x 12x ürev : T Çözüm 2 alıp, 0’a eşitleyelim. 78x 36x 0 x 78 36x 0 78 36x 0 78 13 36x 78 x dır. 36 6 Üçüncü sayı 13 4x 13 4 2 13 6 3 26 13 13 buluruz. 3 3
www.matematikkolay.net (12 sinx).(8 sinx) çarpımının alabileceği en büyük değer kaçtır? A) 99 B) 81 C) 77 D) 65 E) 52 ı Maksimum minimum problemi olarak düşünelim. İfadenin türevini alalım. 12 sinx 8 sinx 0 cosx 8 si : Çözüm nx cosx 12 sinx 0 8cosx cosx.sinx 12cosx sinxcosx 0 4cosx 2sinxcosx 0 sinxcosx cosx 0 cosx sinx 1 0 cosx 0 veya sinx 1 0 dır. cosx 0 sinx 1 veya sinx 1 dir. sinx 1 olursa en büyük değerini alır. 12 sinx 8 sin x 12 18 1 11.9 99 bulunur. 149
y 4sinx 3cosx in 0, aralığında alabileceği 2 en büyük değer kaçtır? www.matematikkolay.net y 4sinx 3cosx, 0 x 2 türev alıp, 0’a eşitleyelim. y’ 4cosx 3sinx 0 4cosx : 3sinx 4 sinx 3 cosx Çözüm 4 tanx bu x açısının sinüs 3 ve kosinüs değerlerini bulalım. 3- 4 – 5 üçgninden yararlanabiliriz. 4 3 sinx , cosx tir. Buna göre; 5 5 4 3 16 9 25 y 4 3 5 buluruz. 5 5 5 5 5 91
f(x) 8cosx 15sinx fonksiyonunun alabileceği en büyük değer kaçtır? A) 7 B) 8 C) 15 D) 17 E) 23 www.matematikkolay.net Türevini 0’a eşitleyelim. f ‘(x) 8sinx 15cosx 0 8sinx 15cosx sinx 15 15 tanx cosx 8 8 8,15 : Çözüm ,17 üçgeninde 15’i gören açının, 2.bölgedeki veya 4.bölgedeki eşiti. Buna göre; f(x)’in en büyük olması için 4.bölg edeki açıyı kullanalım. 8 15 64 225 f(x) 8cosx 15sinx 8 15 17 17 17 17 2 89 17 buluruz. 17 57
f(x) cos2x 2cosx 3 eğrisinin , aralığında alabileceği en büyük 2 2 değer kaçtır? A) 4 B ) 2 C) 1 D) 0 E) 1 www.matematikkolay.net Türev alıp, 0’a eşitleyelim: f ‘(x) cos2x 2cosx ‘ 2sin2x 2sinx 2sin2x 2sinx 0 2s : inx 2sin2x sin Çözüm x sin2x sinx 2.sinxcosx sinx(1 2cosx) 0 kritik noktalar sinx 0 x 1 4 8 ve cosx x , 2 6 6 Bu noktaları denersek; f(x) cos2x 2cosx x f(x) 1 2.1 1 4 1 1 3 x f(x) 2. 6 2 2 2 8 1 1 x f(x) 2. 6 2 2 3 2 En büyük değer 1 buluruz. Doğru Cevap : C şıkkı 10

