Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında Dönüm Noktası ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

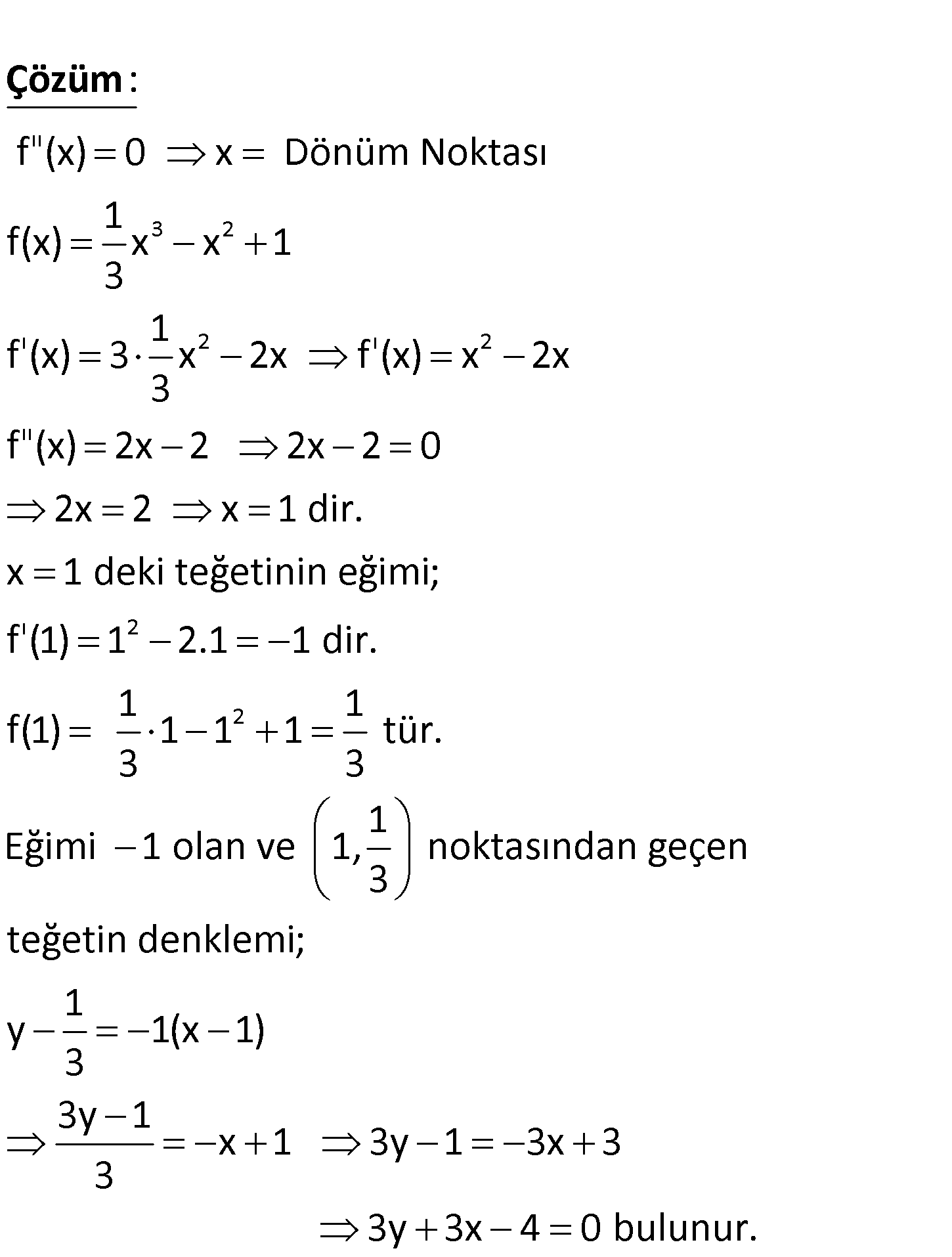
3.SORU


4.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3 2 f(x) x bx cx b fonksiyonunun (1, 3) noktasında dönüm noktasına sahip ise (b, c) ikilisini bulu nuz. www.matematikkolay.net Fonksiyonun ikinci türevini 0 yapan x değeri,dönüm noktasının apsisidir.Fonksiyonun ikin : ci tü Çözüm 3 2 2 3 2 3 2 revini bulup, x 1 noktasındaki değerini 0’a eşitleyelim. f(x) x bx cx b f ‘(x) 3x 2bx c f “(1) 6x 2b f “(x) 6.1 2b 0 6 2b b 3 tür. f(x) x bx cx b x 3x cx 3 (1,3) noktası bu fonksiyonu sağlayan bir değer 3 2 ise; f(1) 3 olmalı. f(1) 1 3(1) c.1 3 3 c 5 3 c 8 dir. (b,c) (3,8) buluruz. 16
3 2 1 f(x) x x 1 3 fonksiyonunun dönüm noktasından çizilen teğetin denklemi aşağıdakilerden ha ngisidir? A) y x 1 0 B) y x 2 0 C) 2y 3x 2 0 D) 3y 3x 2 0 E) 3y 3x 4 0 www.matematikkolay.net ıı 3 2 ı 2 ı 2 ıı f (x) 0 x Dönüm Noktası 1 f(x) x x 1 3 1 f (x) 3 x 2x f (x) x 2x 3 f (x) 2x 2 2x 2 0 2 : Çözüm ı 2 2 x 2 x 1 dir. x 1 deki teğetinin eğimi; f (1) 1 2.1 1 dir. 1 1 f(1) 1 1 1 tür. 3 3 1 Eğimi 1 olan ve 1, noktasından geçen 3 teğetin denklemi; 1 y 1(x 1) 3 3y 1 x 1 3y 1 3x 3 3 3y 3x 4 0 bulunur. 39
www.matematikkolay.net 3 x y 3x a eğrisinin dönüm noktası 3 y x 1 0 doğrusu üzerinde olduğuna gör e, a kaçtır ? 3 2 3 Dönüm noktasında y ” 0 dır. x 3x a ” 0 3 x 3 ‘ 0 2x 0 x 0 dır. x x 0 için y 3x a 3 : Çözüm a dır. Demek ki dönüm noktası 0, a noktasıdır. Bu nokta y x 1 0 doğrusu üzerinde ise; a 0 1 0 a 1 0 a 1 dir. 120
4 3 2 f(x) cx 2x x 3 fonksiyonunun dönüm nok – tası olmadığına göre, c nin alabileceği en küçük tam a s yı değeri kaçtır? www.matematikkolay.net 3 2 2 2 Dönüm noktası için ikinci türeve bakılır. f ‘(x) 4cx 6x 2x f ”(x) 12cx 12x 2 12cx : 12x 2 de Çözüm 2 nkleminin iki farklı kökü yok ise 0 dır. 12 4 12c .2 0 144 96c 0 144 96c 96 2 c 144 3 2c 3 3 c dir. c en az 2 olabilir. 2 121

