Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında Daima artan, daima azalan ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

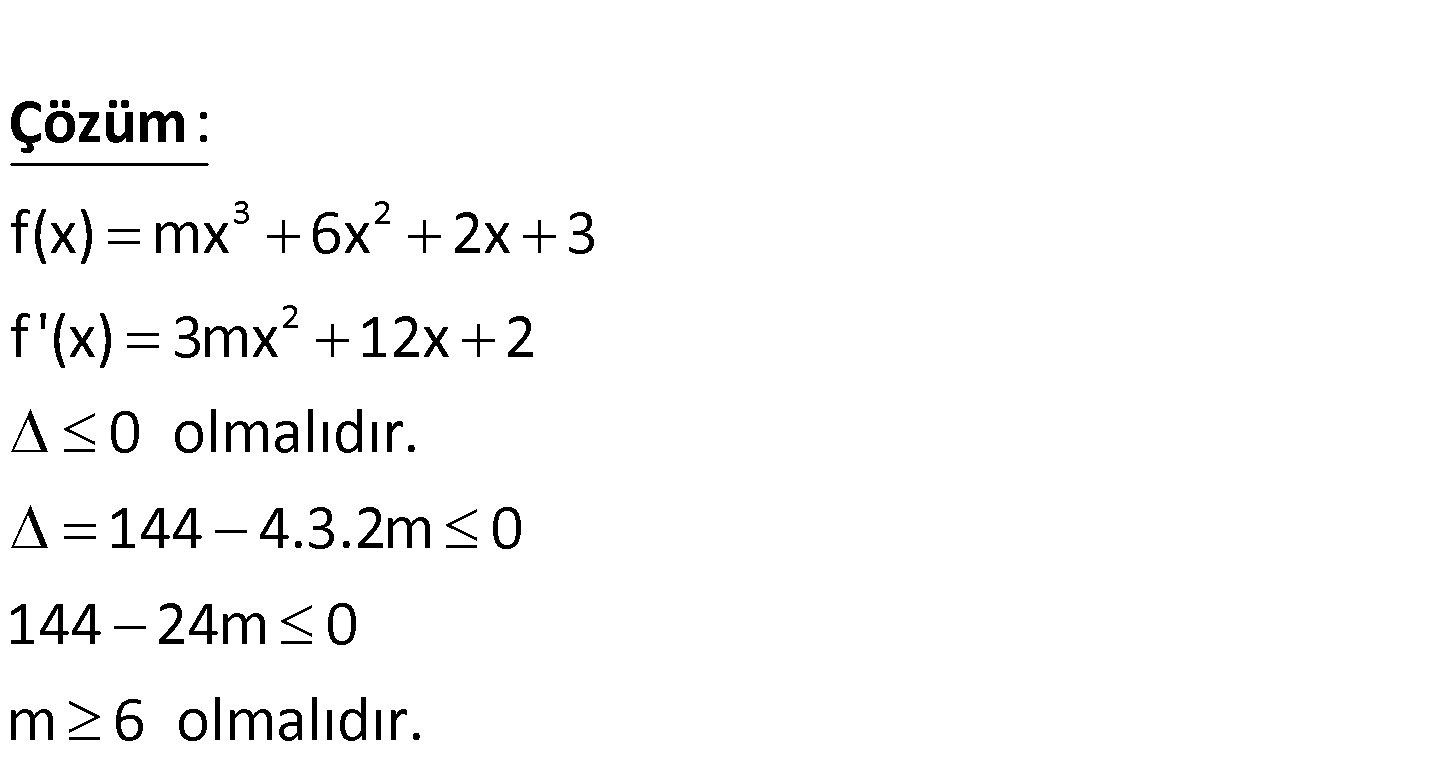
2.SORU


3.SORU


4.SORU


5.SORU


6.SORU

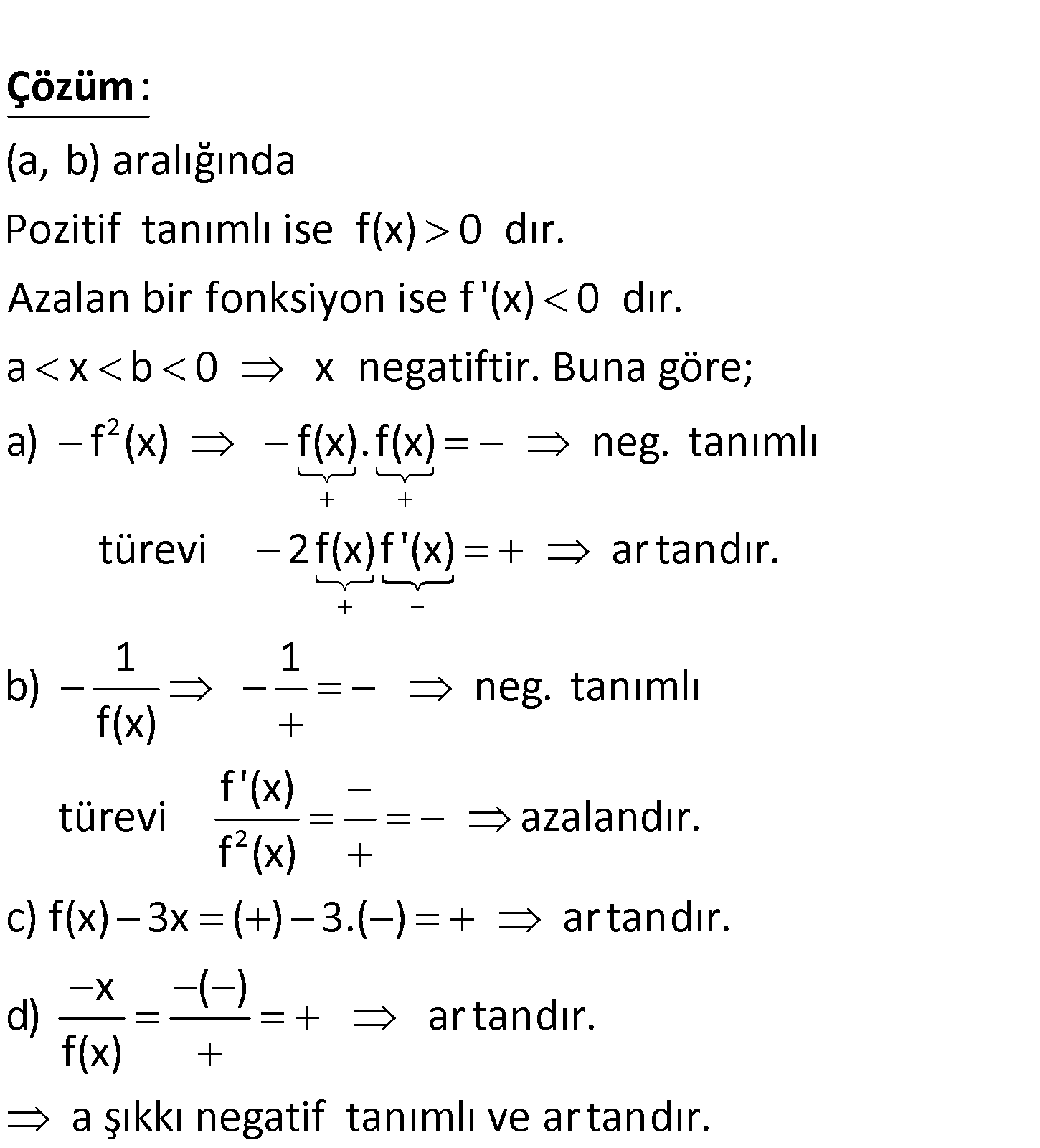
7.SORU


8.SORU


9.SORU


10.SORU


11.SORU

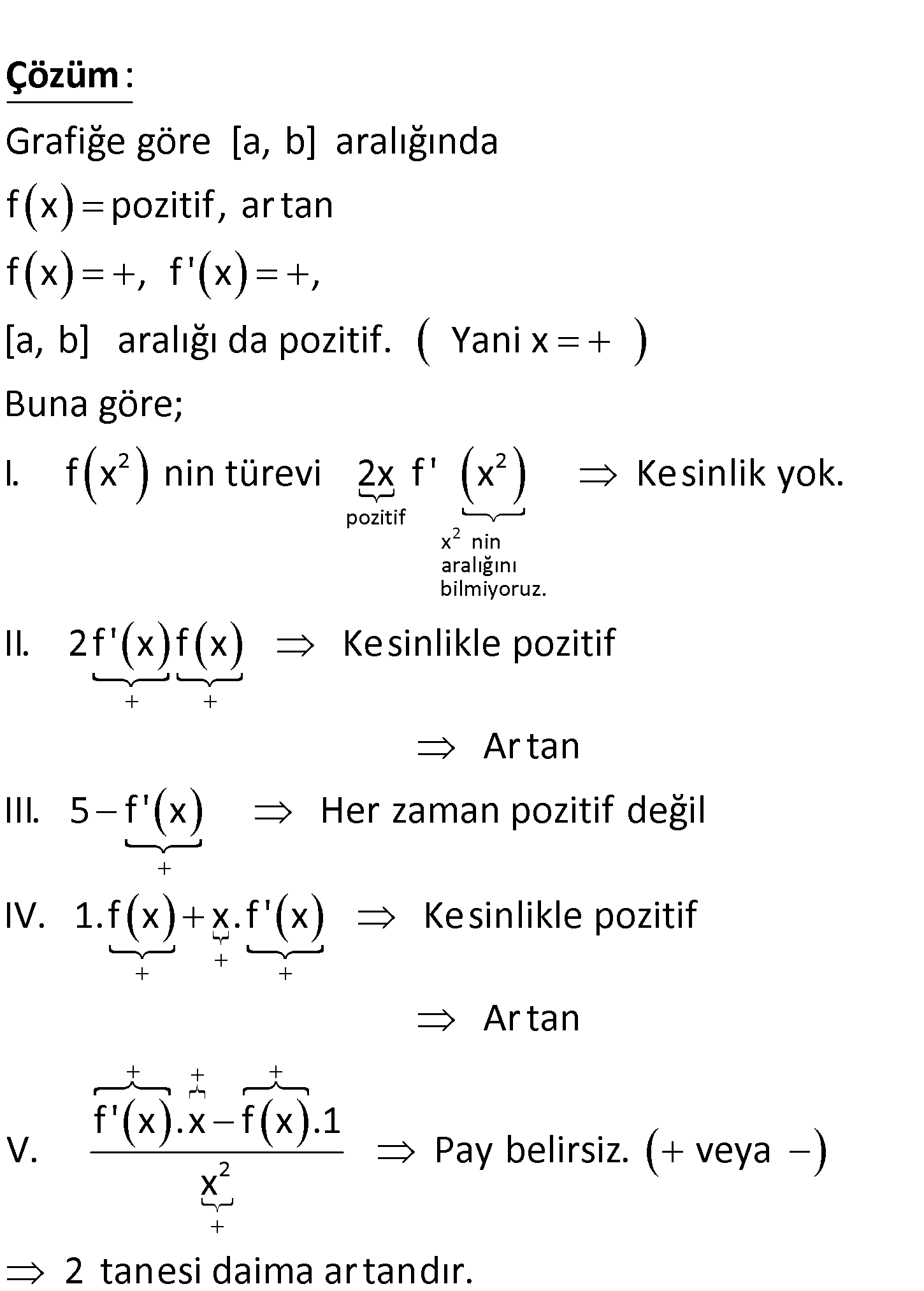
12.SORU


13.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
Daima artan, daima azalan
3 2 f(x) mx 6x 2x 3 fonksiyonu daima ar tan olduğuna göre, m nin en geniş değer aralığı aşağı dakilerden hangisidir? A) m 6 B) m 6 C)m 0 D) 0 m 6 E) 6 m 12 www.matematikkolay.net 3 2 2 f(x) mx 6x 2x 3 f ‘(x) 3mx 12x 2 0 olmalıdır. 144 4.3.2m 0 144 24m 0 m 6 olmalıd : ır. Çözüm 3
3 2 f(x) ax 4x x 2 fonksiyonu x R için azalan bir fonksiyon ise a’nın değer aralığı nedir ? www.matematikkolay.net 2 1.türevi sürekli pozitif olmalıdır. f ‘(x) 0 3ax 8x 1 0 Bu denklemin iki kökü olmaması lazı : m. Çözüm 2 0 olmalıdır. ( 8) 4.3a.( 1) 0 64 12a 0 12a 64 64 16 a a buluruz. 12 3 56
3 2 c nin hangi değerleri için f(x) x 3x cx 1 fonksiyonu daima ar tandır? www.matematikkolay.net ı 3 2 ı 2 2 f (x) 0 f fonksiyonu ar tandır. f(x) x 3x cx 1 f (x) 3x 6x c 0 0 olmalı. b 4ac 0 36 4.3 : c Çözüm 0 36 12c c 3 [3, ) bulunur. 74
www.matematikkolay.net y f(x) fonksiyonu x R için azalan ve pozitif değerli bir fonksiyondur. Buna göre, aşağıdaki fonksi 2 2 2 2 3 yonlardan hangisi aynı aralıkta daima ar tandır? A) f(x ) B) f (x) C) f (x ) D) 3x f(x) E) f(x) x x , f(x) , f ‘(x) olduğu verilmiş soruda. Şıklardaki fonksiyonların türevini alal : Çözüm 2 2 2 2 2 2 2 3 ım. A) f(x ) 2x.f ‘(x ) 2.( )( ) daima ar tan B) f (x) 2f(x)f ‘(x) 2.( )( ) daima azalan C) f (x ) 2f(x )2x.f ‘(x ) 2.( )( )( ) azalan D) 3x f(x) 3 f ‘(x) 3 ( ) ar tan veya azalan E) f(x) x f 2 ‘(x) 3x daima azalan Cevap: A 78
3 2 f(x) x ax 5x 7 fonksiyonunun yerel ekstremum noktaları olmadı – ğına göre, a nın alabileceği en büyük tam sayı değe – ri kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 2 2 2 2 f ‘(x) in iki farklı kökü olmamalıdır. f ‘(x) 3x 2ax 5 0 olmalıdır. 4a 4.3.5 0 4a 4.1 0 a : 5 Çözüm 15 a en fazla 3 olabilir. www.matematikkolay.net 84
a b 0 olmak üzere, f fonksiyonu (a, b) aralığında pozitif tanımlı ve aza – lan bir fonksiyondur. Buna 2 göre, aynı aralıkta aşağıdaki fonksiyonlardan hangileri negatif tanımlı ve ar tandır? 1 A) f (x) B) f(x) x C) f(x) 3x D) f(x) www.matematikkolay.net Pozitif tanımlı ise f(x) 0 dır. Azalan bir fonksiyon ise f ‘(x) 0 dır : (a, b) aralığınd . x a a Çözüm 2 2 b 0 x negatiftir. Buna göre; a) f (x) f(x). f(x) neg. tanımlı türevi 2f(x)f ‘(x) ar tandır. 1 1 b) neg. tanımlı f(x) f ‘(x) türevi azalandır. f (x) c) f(x) 3x ( ) 3.( ) ar tandır. x ( ) d) ar tandır. f(x) a şıkkı negatif tanımlı ve ar tandır. 97
(0, ) aralığında f(x) pozitif değerli ve azalan bir fonksiyondur. Buna göre, aşağıdaki fonksiyonla 2 rdan hangisi aynı aralıkta daima azalandır? A) f( x) B) f(x) C) 2f(x) D) f( x ) E) x f(x) www.matematikkolay.net işareti bilmi f(x) ve f ‘(x) dir. Şıklara bakıp türev alalım. A) f( x) türevi f ‘( x) : Çözüm yoruz 2 2 işareti bilmiyoruz işaretini bilemiyoruz. B) f(x) türevi f ‘(x) ar tan C) 2f(x) türevi 2f ‘(x) azalan D) f( x ) türevi 2x f ‘( x ) işrt bilemiyoruz. E) x f(x) türevi 1 f ‘(x) ar tan Cevap: C 104
3 2 f(x) (1 a)x 3x x 3 fonksiyonunun daima ar tan olabilmesi için a’nın aralığı aşağıdakiler den hangisidir? A) ( , 2] B) ( , 1] C) [ 2, 1] D) [1, ) E) ( , 1] 2 2 Daima ar tan olabilmesi için, f ‘(x) 0 olmalıdır. 3(1 a)x 6x 1 0 3 3a x 6x 1 0 0 olmalıdır. : 0 b Çözüm 2 4.a.c 0 36 4. 3 3a .1 0 36 4. 3 3a 0 36 12 12a 0 12a 24 0 12a 24 a 2 dir. Cevap: A 116
www.matematikkolay.net 3 f : R R f(x) x 27x fonksiyonunun ar tan olduğu en geniş aralık aşağı – dakilerden hangisidir ? A) ( , 3] [3, ) B) ( 3, 3) C) [ 3, 3] D) ( , 3) (3, ) E) [3, ) 2 2 f ‘(x) 0 3x 27 0 x 9 0 x 3 x 3 0 x 3 ve x 3 olursa bu eşitsizlik sağlanır. x değeri : ( , 3 Çözüm ] [3, ) aralığında iken bu fonksiyon ar tandır. Cevap: A www.matematikkolay.net 117
www.matematikkolay.net 3 2 fonksiyonu gerçek sayılar kümesinde birebir ve ar – ta f(x) x n bir fonksiyo 2x ax ndur. Bu 5 n a göre, a’nın alabileceği en küçük tam sayı değeri kaçtır? A) 1 B) 0 C) 1 D) 2 E) 3 2 2 Sürekli ar tan ise, f ‘(x) 0 olmalıdır. 3x 4x a 0 ise 3x 4x a denkleminin iki farklı k kü : ö Çözüm 2 olmamalıdır. Yani 0 olmalıdır. 4 4.3.a 0 16 12a 0 16 12a 4 3a 4 4 a a tür. 3 3 a’nın en küçük tam sayı değeri 2 olacaktır. 156
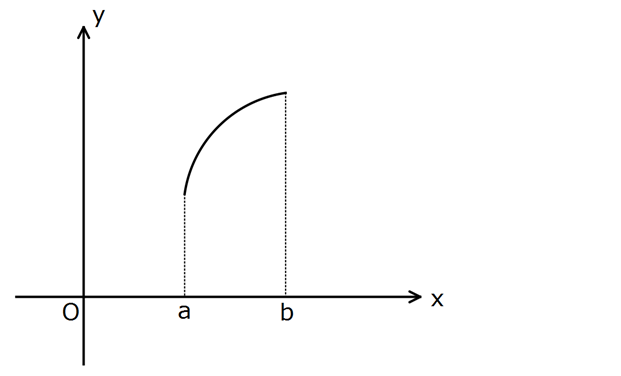
www.matematikkolay.net Şekilde yf(x) fonksiyonuna ait eğrinin [a, b] aralı-ğında kalan parçasına ait grafik verilmiştir.22 Buna göre;I.f(x)II.f(x)III.5xf(x)IV.x.f(x)f(x)V.xfonksiyonlarından kaç tanesi aynı aralıkta daimaartandır?A) 1B) 2C) 3D) 4E) 5 www.matematikkolay.net Grafiğe göre [a, b] aralığında f x pozitif, ar tan f x , f ‘ x , [a, b] aralığı da pozitif : Çözüm 2 2 2 pozitif x nin aralığını bilmiyoruz. . Yani x Buna göre; I. f x nin türevi 2x f ‘ x Kesinlik yok. II. 2f ‘ x f x Kesinlikle pozitif Ar tan III. 2 5 f ‘ x Her zaman pozitif değil IV. 1. f x x. f ‘ x Kesinlikle pozitif Ar tan f ‘ x .x f x .1 V. Pay belirsiz. veya x 2 tanesi daima a r tandır. 168
f(x) fonksiyonu ( 5, 5) aralığında negatif değerli ve ar tan bir fonksiyondur. Aşağıdakilerden hangis 2 4 2 i aynı aralıkta ar tandır? 1 A) B) f (x) C) f(x) x f(x) 1 D) f (x) E) f (x) www.matematikkolay.net Negatif değerli ise f x dir. Ar tan ise f ‘ x dır. Şimdi şıklara bakalım. Türevleri po : z Çözüm 2 2 4 3 3 itif olmalıdır. 1 f ‘ x A) ‘ Azalan f x f x B) f x ‘ 2f x f ‘ x 2. Azalan C) f x x ‘ f ‘ x 1 1 Garanti değil. f ‘ x değeri 1’den küçük ise azalan olur. D) f x ‘ 4f x f ‘ x 4 Azal ‘ 2 3 2 3 an 1 2 E) f x ‘ 2f x .f ‘ x f ‘ x f x f x Ar tandır. Cevap : E 170
3 2 f(x) x ax 6x fonksiyonu daima ar tan bir fonksiyon olduğuna göre, a nın alabileceği kaç farklı d oğal sayı değeri var dır? A) 3 B) 4 C) 5 D) 6 E) 7 2 2 f ‘(x) 0 daima sağlanmalıdır. 3x 2ax 6 0 daima olması için 0 olmalıdır 2 4. : . 0 a Çözüm 2 2 2 3.6 0 4a 72 0 4a 72 a 18 a 0,1,2,3,4 olabilir 5 farklı doğal sayı

