Soru Sor sayfası kullanılarak Türev konusu altında Üstel Fonskiyonların Türevi, e üzeri x in türevi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
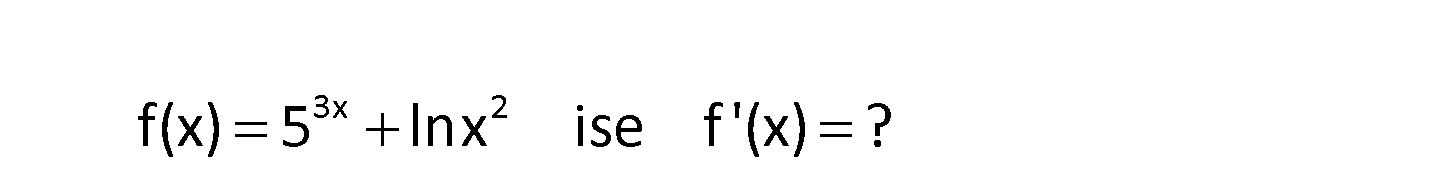

2.SORU
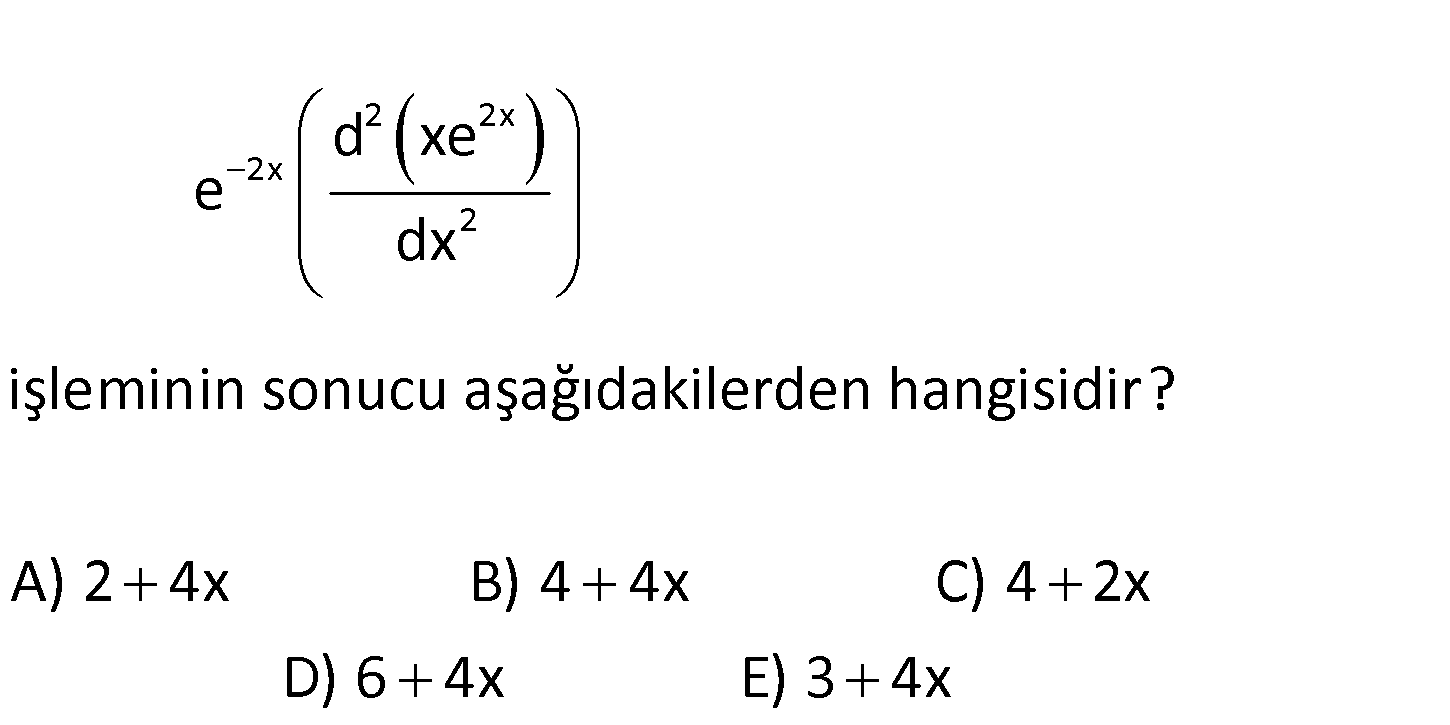
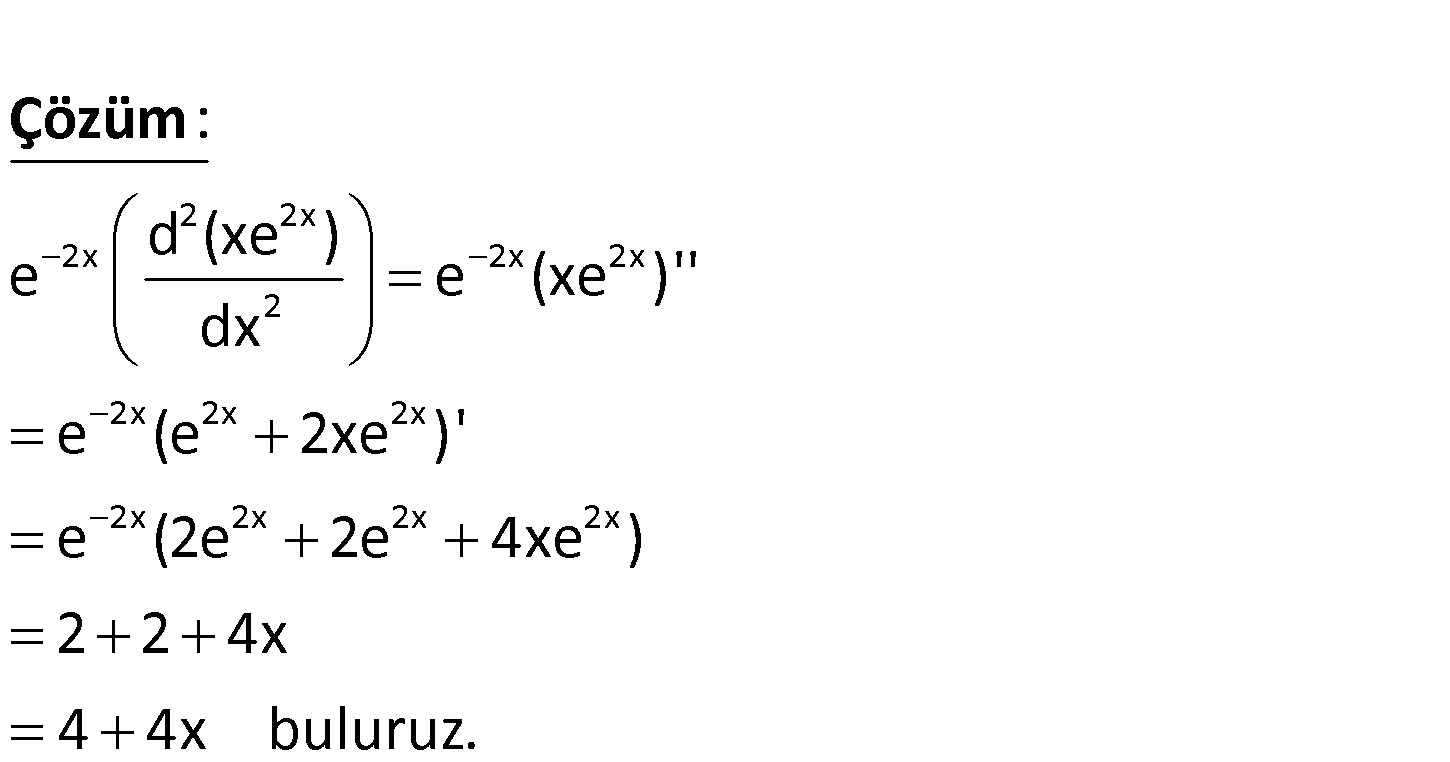
3.SORU


4.SORU
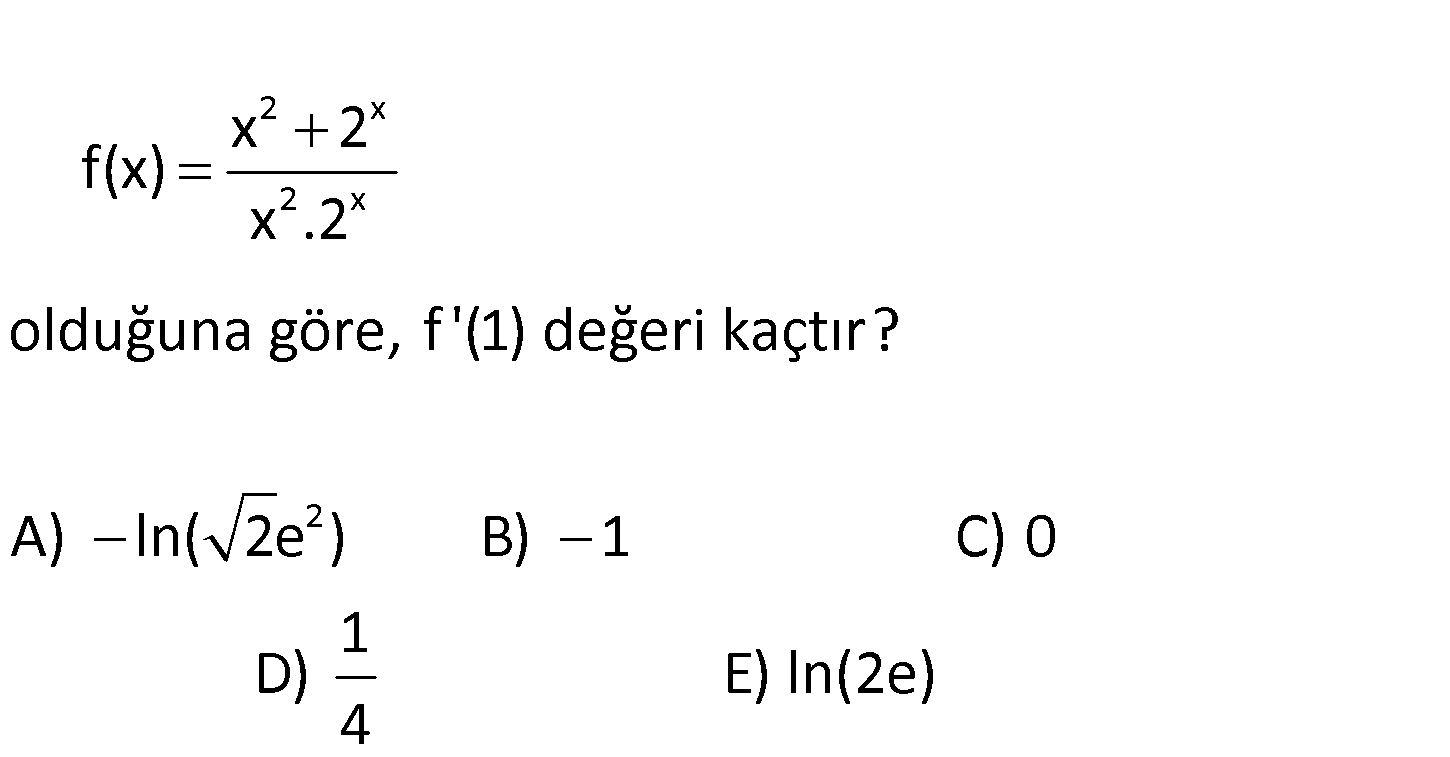
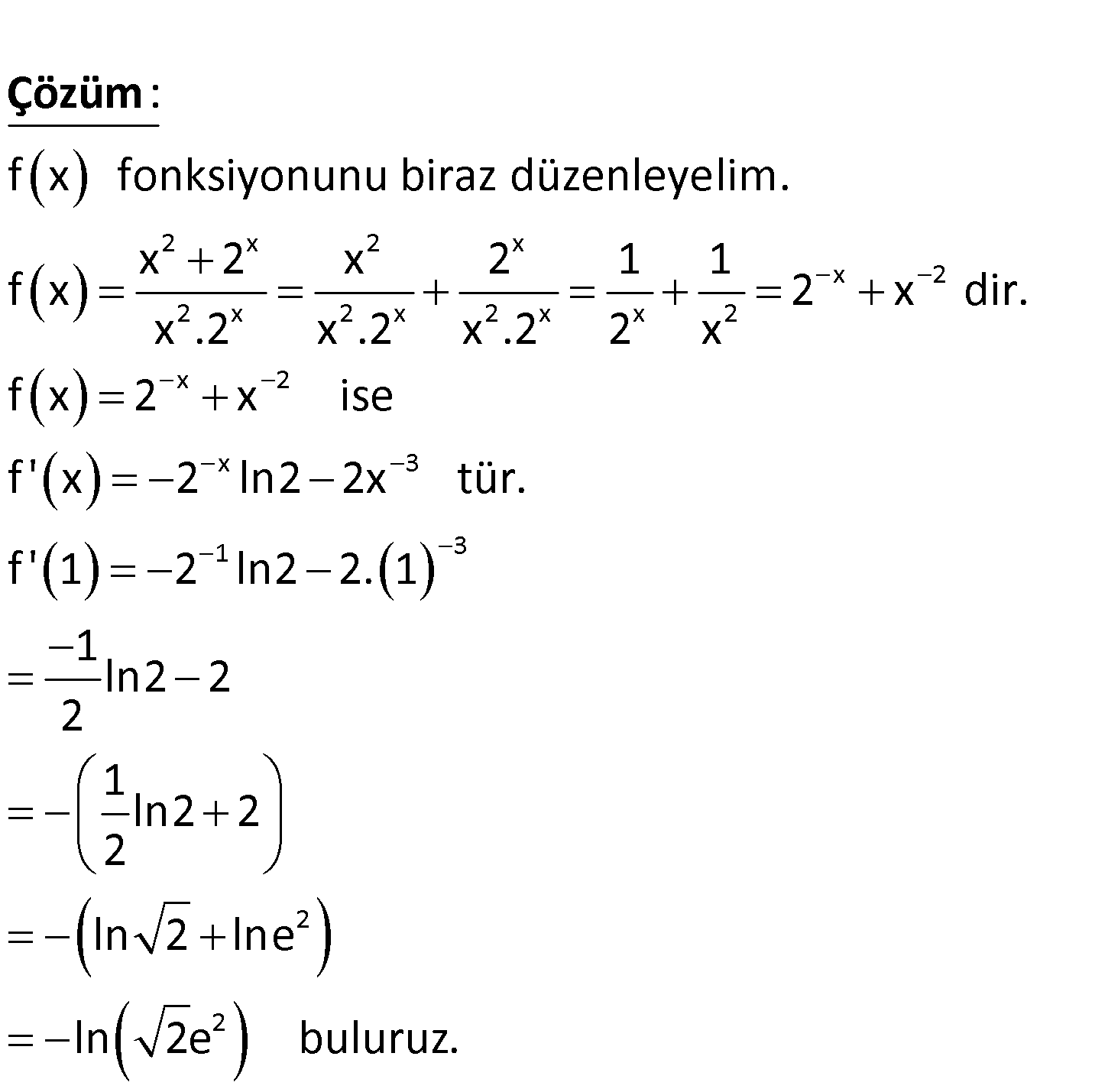
5.SORU
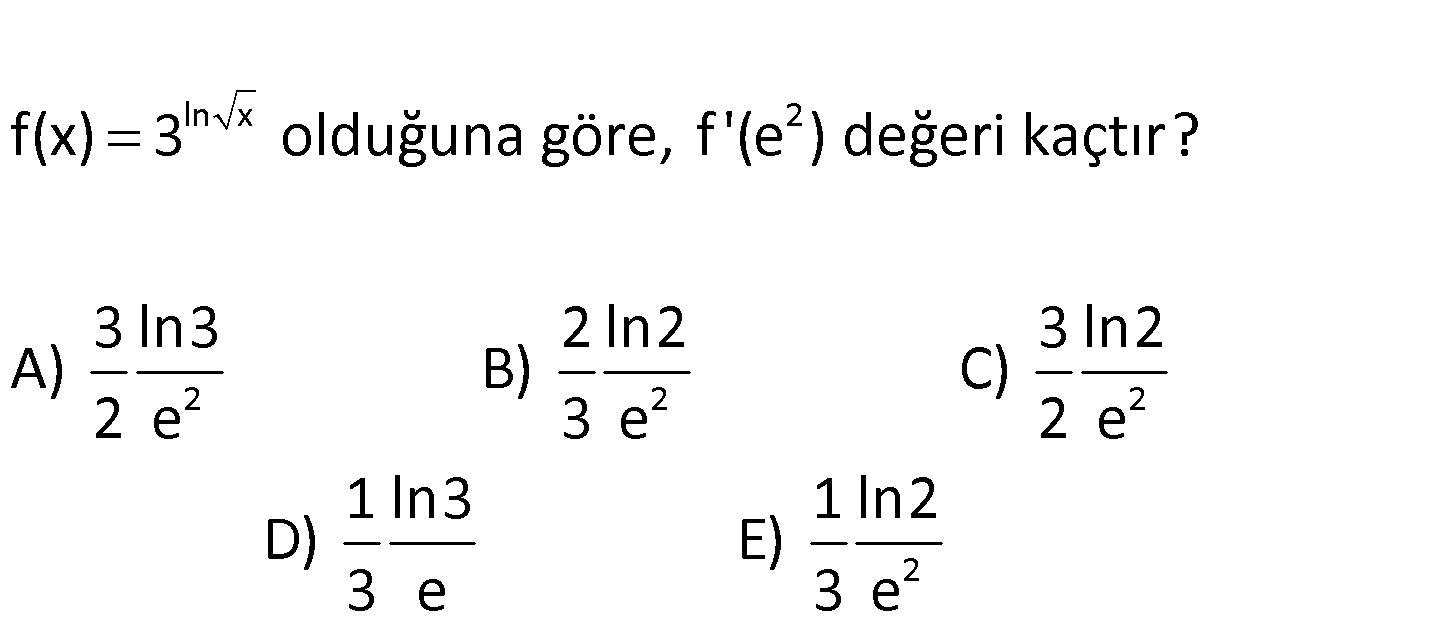
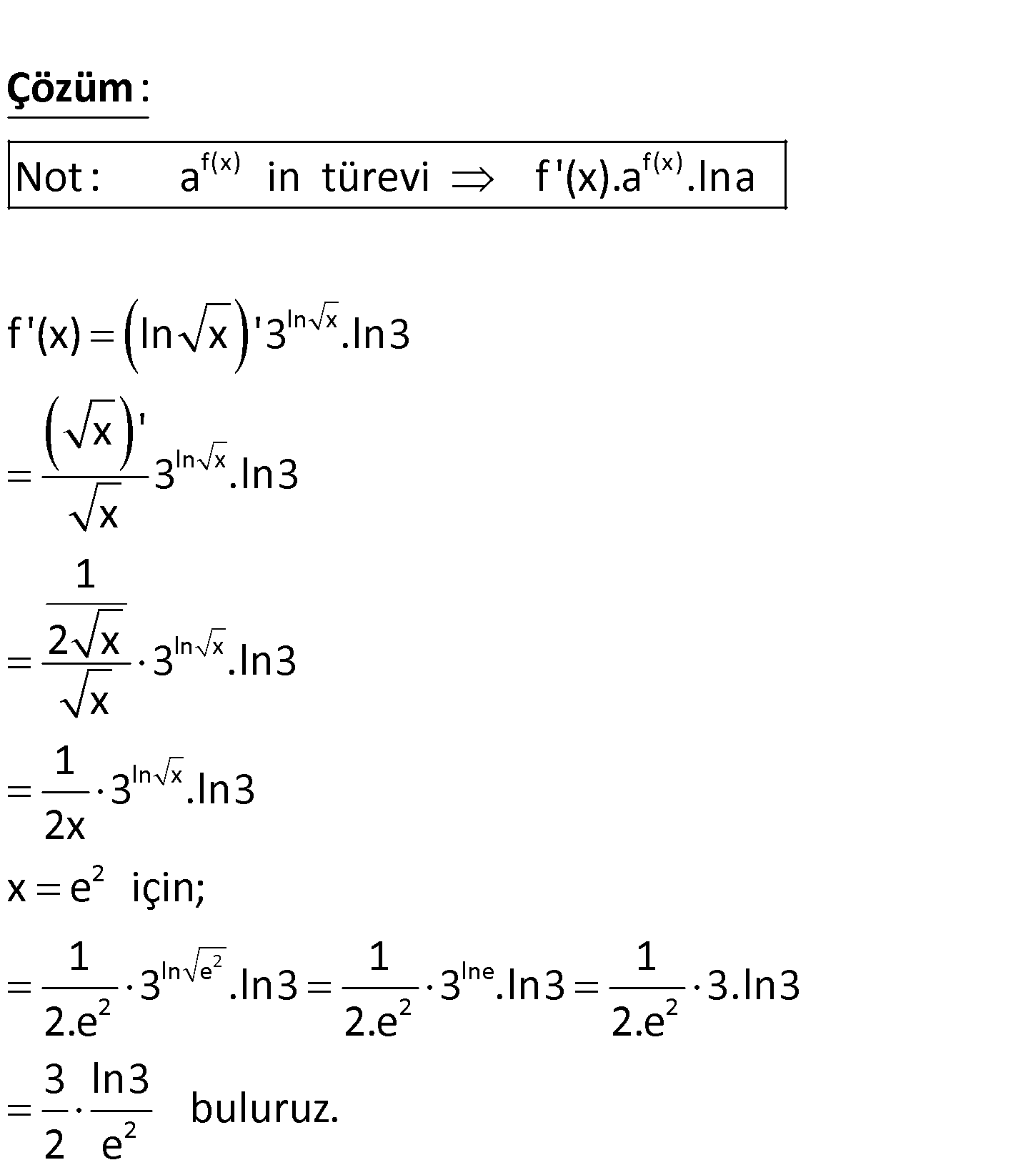
6.SORU
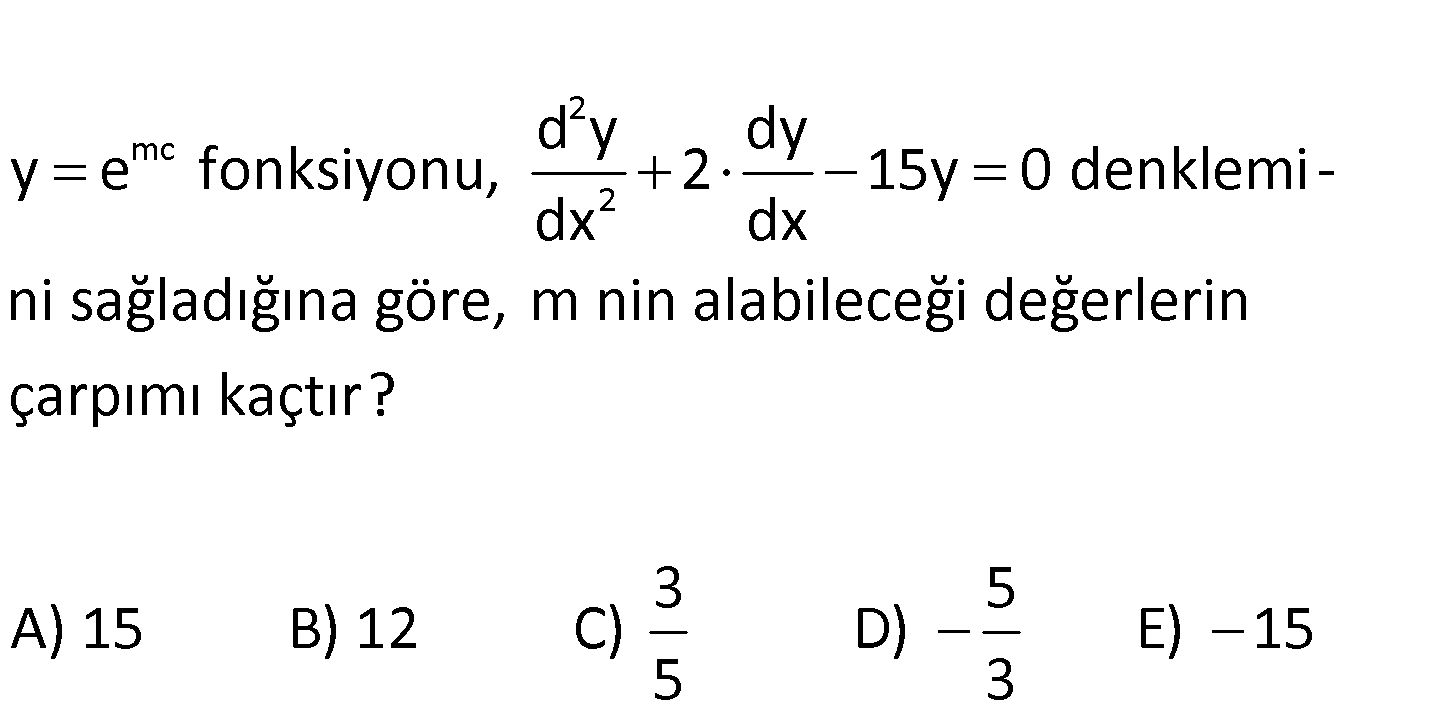

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3x 2 f(x) 5 lnx ise f ‘(x) ? f(x) f(x) 3x 2 3x 3x Not : a in türevi f ‘(x).a .lna f(x) 5 lnx f(x) 5 2lnx f ‘(x) 3x ‘5 : .ln5 Çözüm 3x 2 x 2 f ‘(x) 3.5 .ln5 buluruz. x www.matematikkolay.net 109
2 2x 2x 2 d xe e dx işleminin sonucu aşağıdakilerden hangisidir? A) 2 4x B) 4 4x C) 4 2 x D) 6 4x E) 3 4x www.matematikkolay.net 2 2x 2x 2x 2x 2 2x 2x 2x 2x 2x 2x 2x d (xe ) e e (xe )” dx e (e 2xe )’ e (2e 2e 4xe ) 2 2 4x 4 4x ul : b Çözüm uruz. 53
x 2 f(x) e (2x 3x 3) fonksiyonu için f ‘(a) 2f(a) eşitliğini sağlayan a reel sayılarının toplamı kaç tır? 7 1 A) 4 B) C) 2 D) E) 3 2 2 x 2 x 2 2 x x 2 x f(x) e (2x 3x 3) f ‘(x) e (2x 3x 3) (2x 3x 3)’.e f ‘(x) e (2x : 3x 3) (4x 3).e f ‘(x) e Çözüm x 2 x 2 a 2 a 2 a ( 2x 3x 3 4x 3) f ‘(x) e ( 2x x) dir. f ‘(a) 2f(a) ise e ( 2a a) 2.e (2a 3a 3) e 2 a ( 2a a) 2. e 2 2 2 2 (2a 3a 3) 2a a 4a 6a 6 2a 7a 6 0 7 Kökler toplamı: buluruz. 2 www.matematikkolay.net 21
www.matematikkolay.net 2 2 x 2 x olduğuna göre, f ‘(1) değeri kaçtır? A) ln( 2e ) B) 1 C) 0 x 2 f(x) x .2 1 D) E) ln(2e) 4 2 x 2 x x 2 2 x 2 x 2 x x 2 x f x fonksiyonunu biraz düzenleyelim. x 2 x 2 1 1 f x 2 x dir. x .2 x .2 x .2 2 x f x : 2 Çözüm 2 x 3 1 3 2 2 x ise f ‘ x 2 ln2 2x tür. f ‘ 1 2 ln2 2. 1 1 ln2 2 2 1 ln2 2 2 ln 2 lne ln 2e buluruz. 136
www.matematikkolay.net ln x 2 2 2 2 f(x) 3 olduğuna göre, f ‘(e ) değeri kaçtır? 3 ln3 2 ln2 3 ln2 A) B) C) 2 e 3 e 2 e 2 1 ln3 1 ln2 D) E) 3 e 3 e f(x) f(x) ln x ln x ln x Not : a in türevi f ‘(x).a .lna f ‘(x) ln x ‘3 .ln3 x ‘ 3 .ln3 x 1 2 x 3 .l x : Çözüm 2 ln x 2 ln e lne 2 2 2 2 n3 1 3 .ln3 2x x e için; 1 1 1 3 .ln3 3 .ln3 3.ln3 2.e 2.e 2.e 3 ln3 buluruz. 2 e 171
www.matematikkolay.net 2 mc 2 d y dy y e fonksiyonu, 2 15y 0 denklemi – dx dx ni sağladığına göre, m nin alabileceği değerlerin ça rpımı kaçtır? 3 5 A) 15 B) 12 C) D) E) 15 5 3 f(x) f(x) 2 mx mx mx mx 2 Not : e in türevi f ‘(x).e tir. y” 2y’ 15y 0 ise m e 2me 15e 0 e m 2m 15 0 : Çözüm mx e m 5 m 3 0 m 3 veya m 5 tir. Bunların çarpımları 15 bulunur. 174

