Soru Sor sayfası kullanılarak Türev konusu altında Sinüsün Türevi, Kosinüsün Türevi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
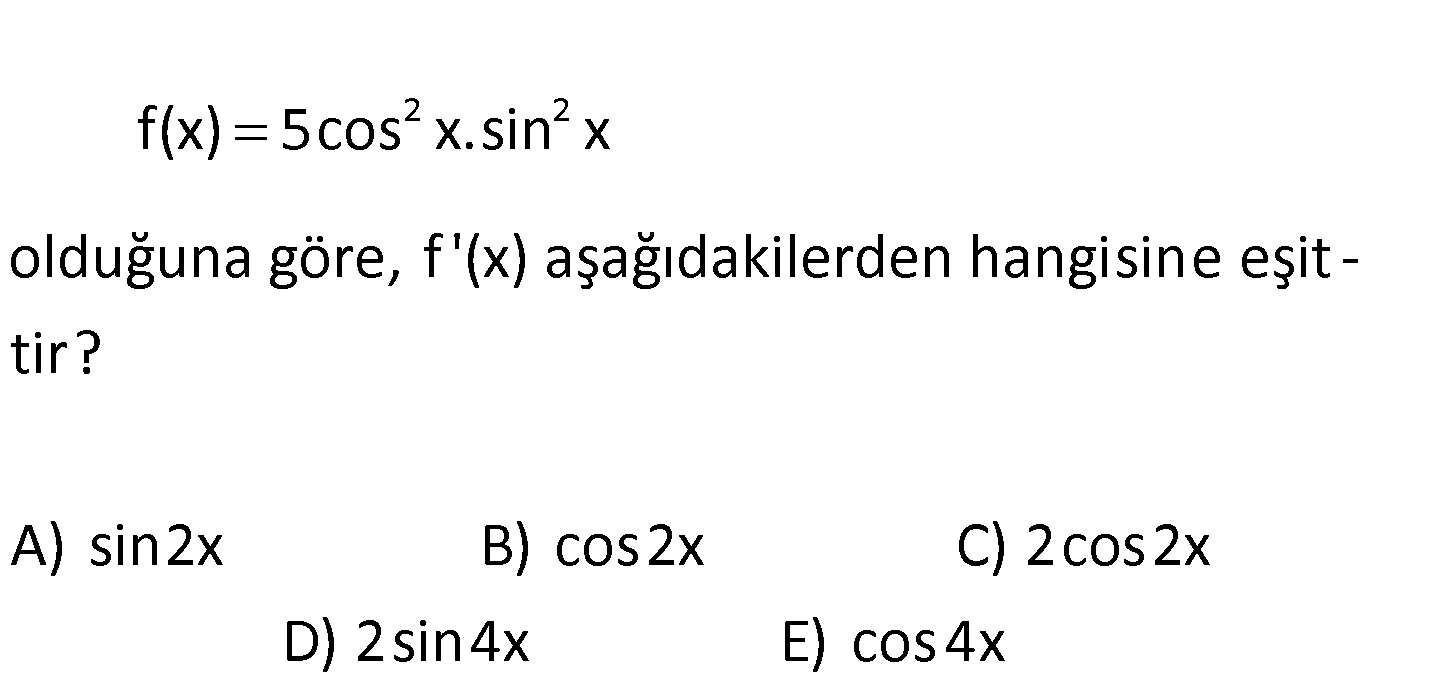
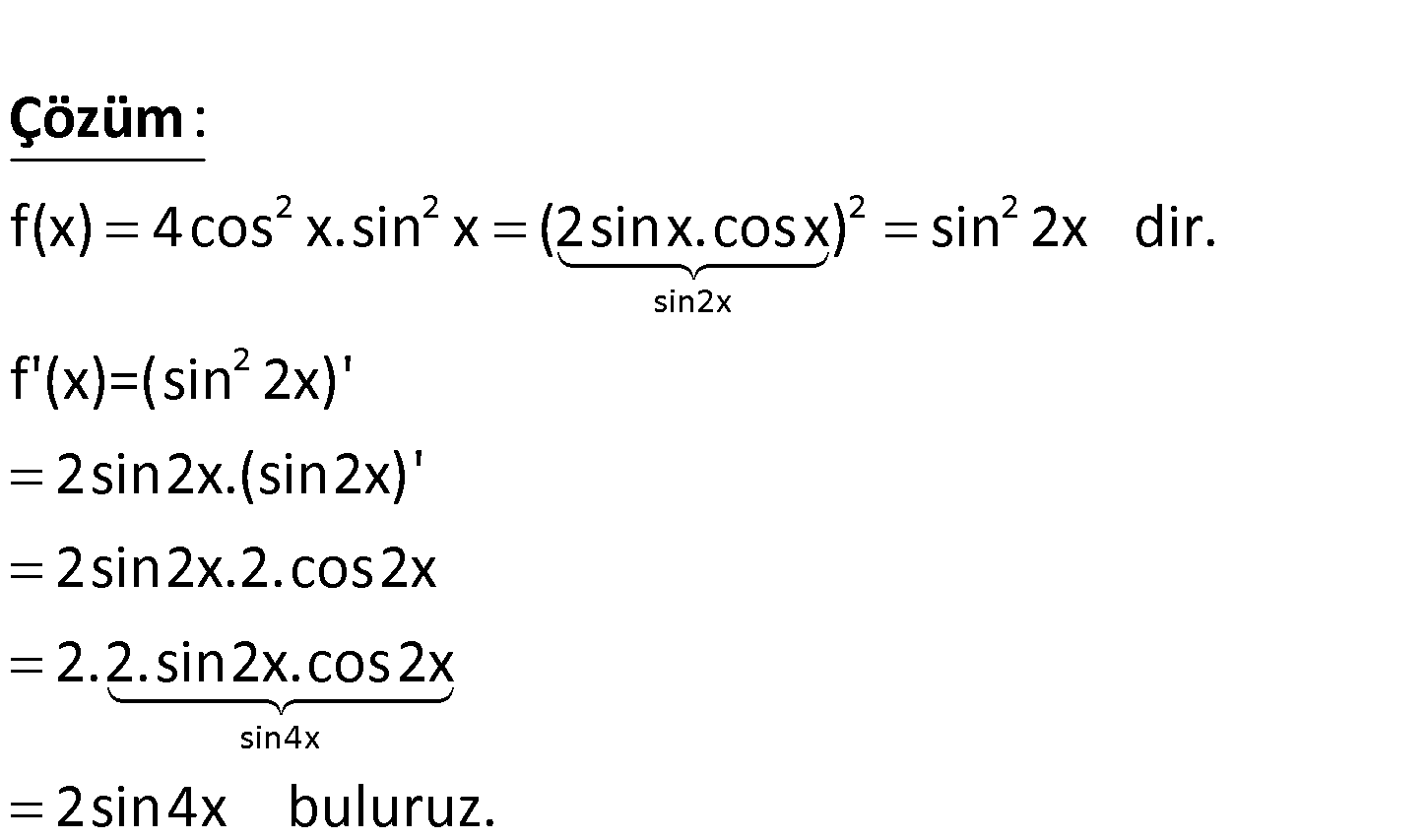
3.SORU
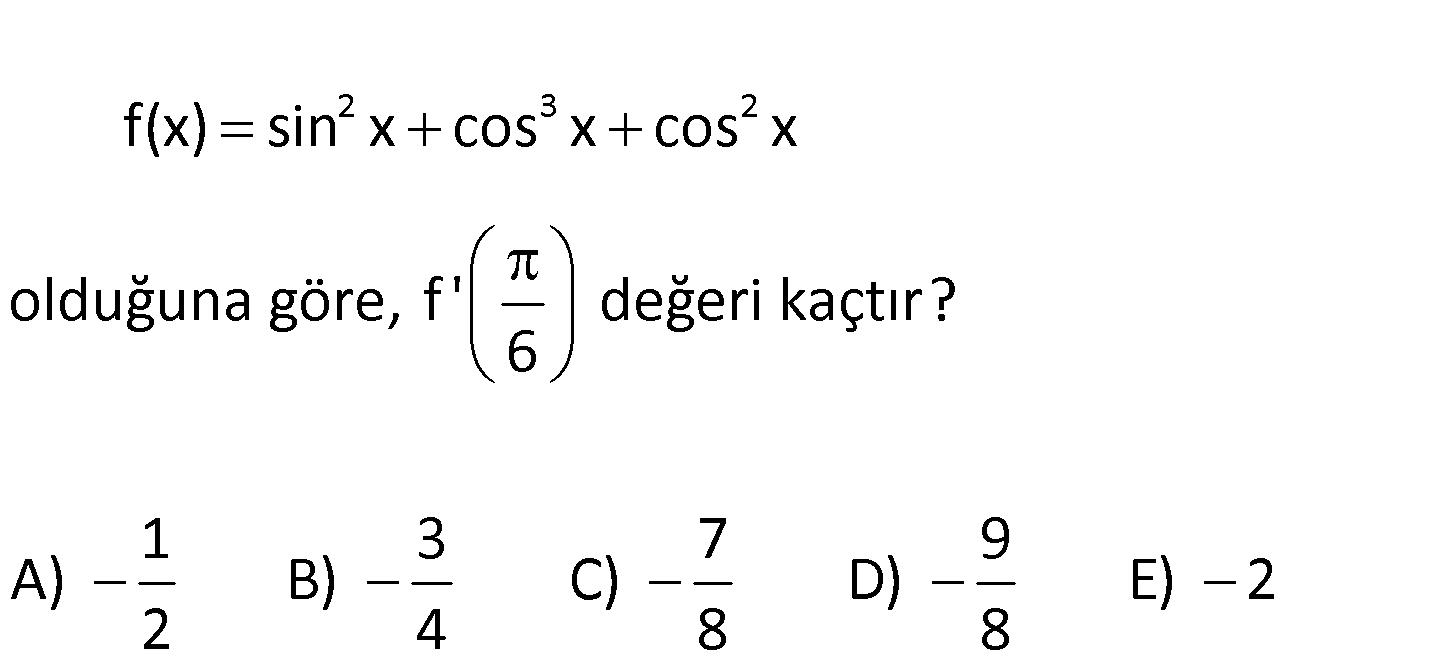
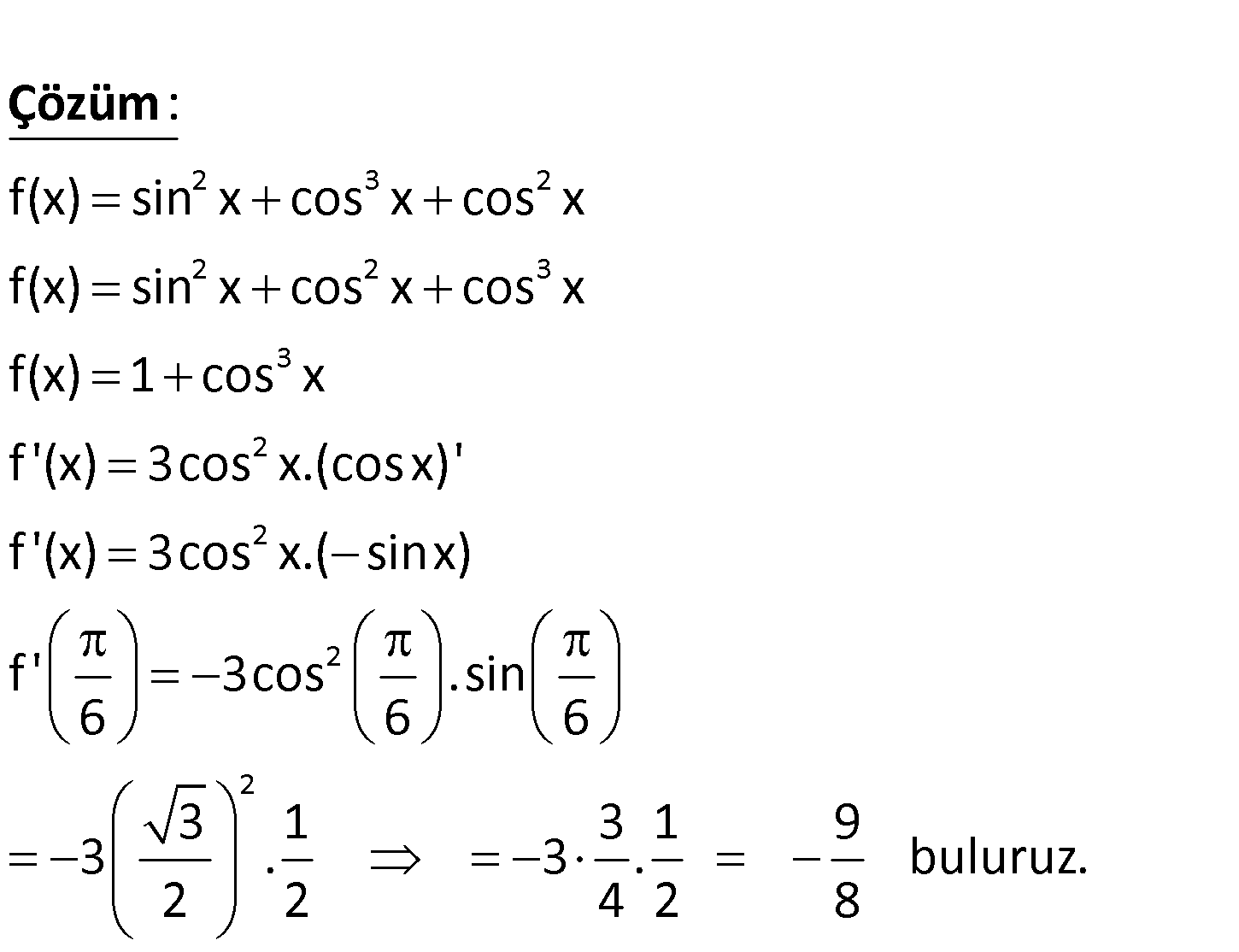
4.SORU
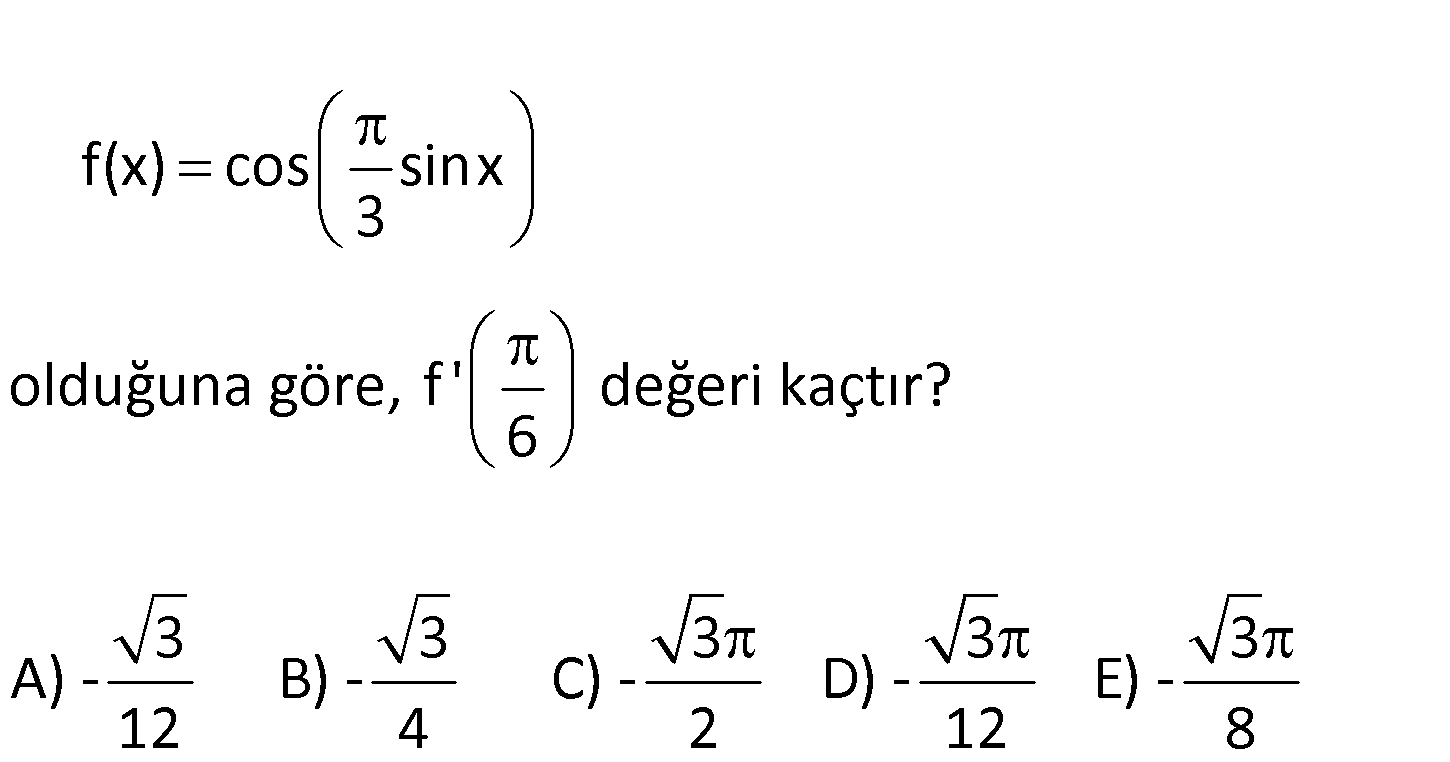
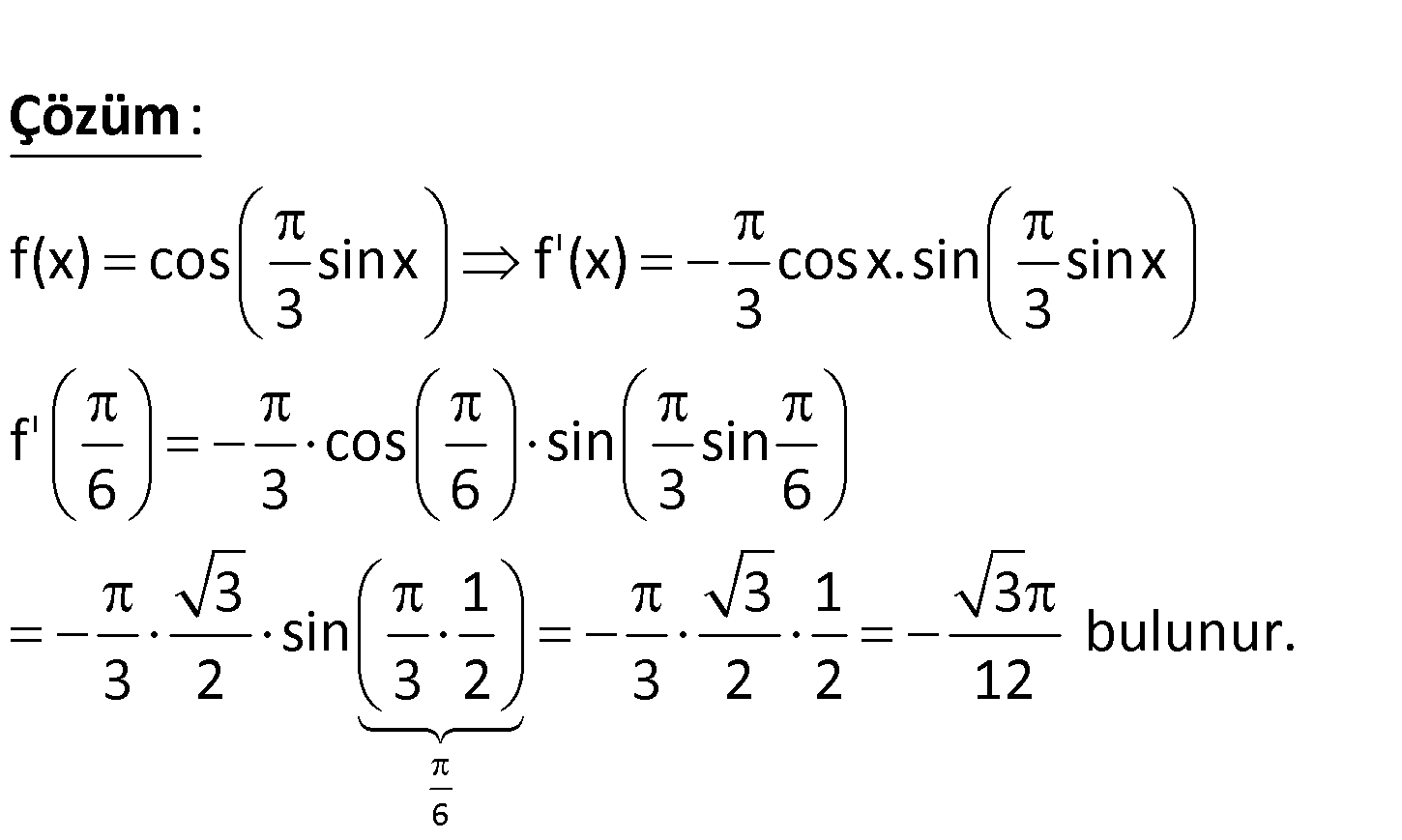
5.SORU
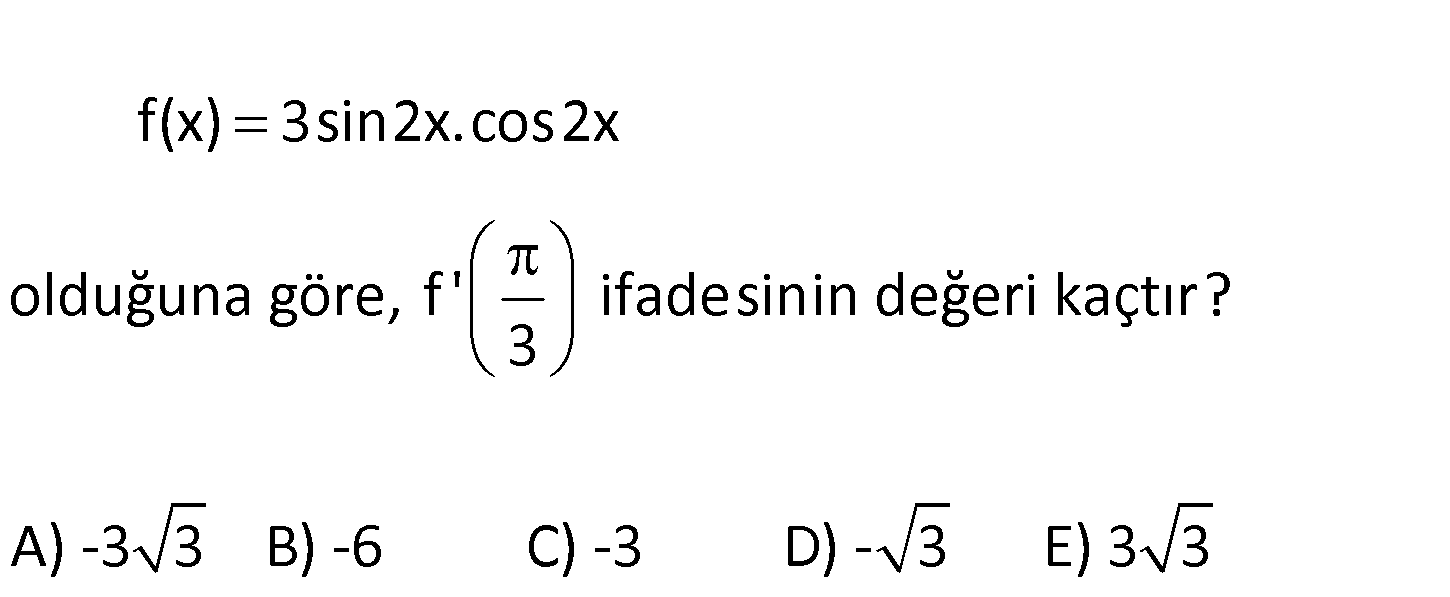

6.SORU
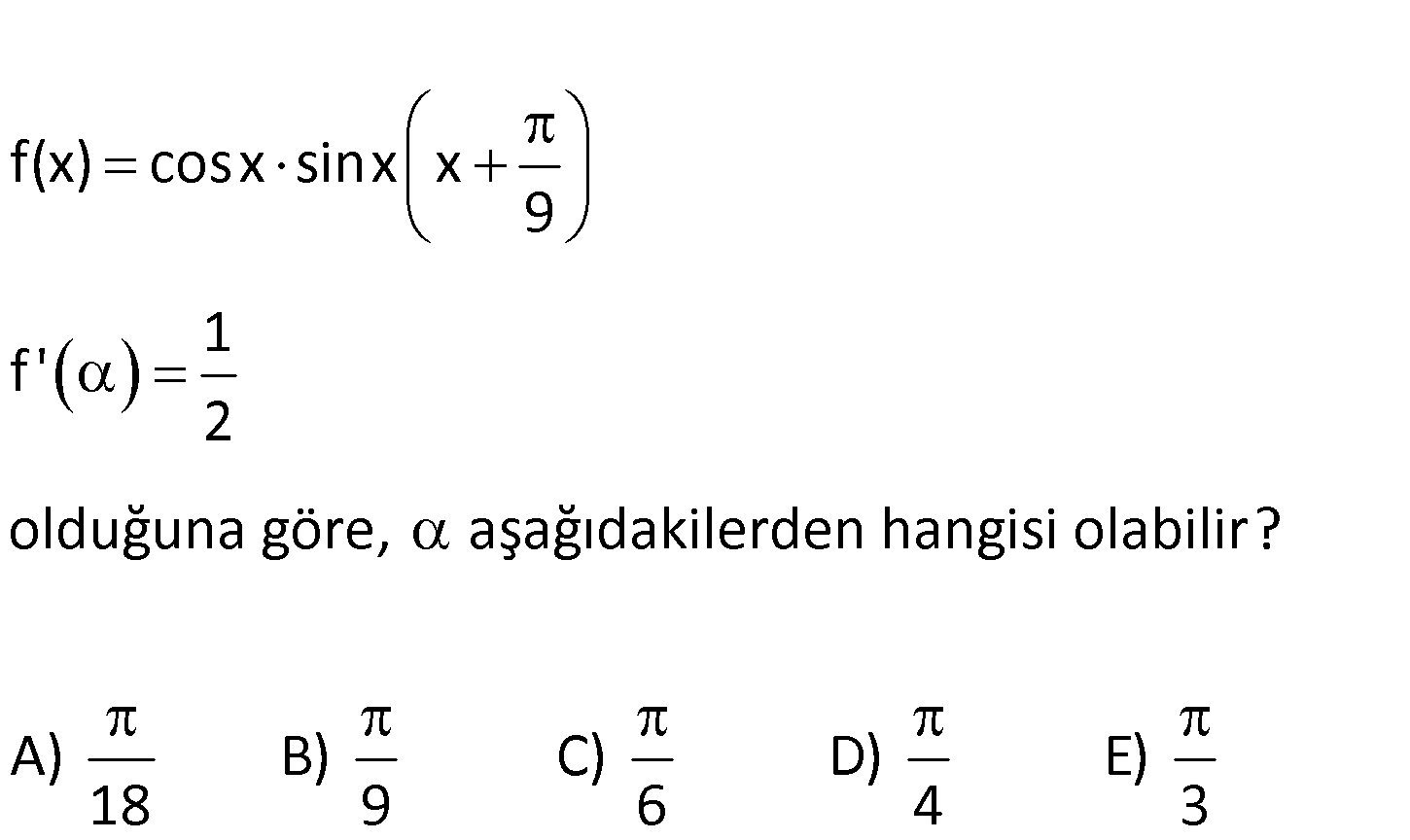
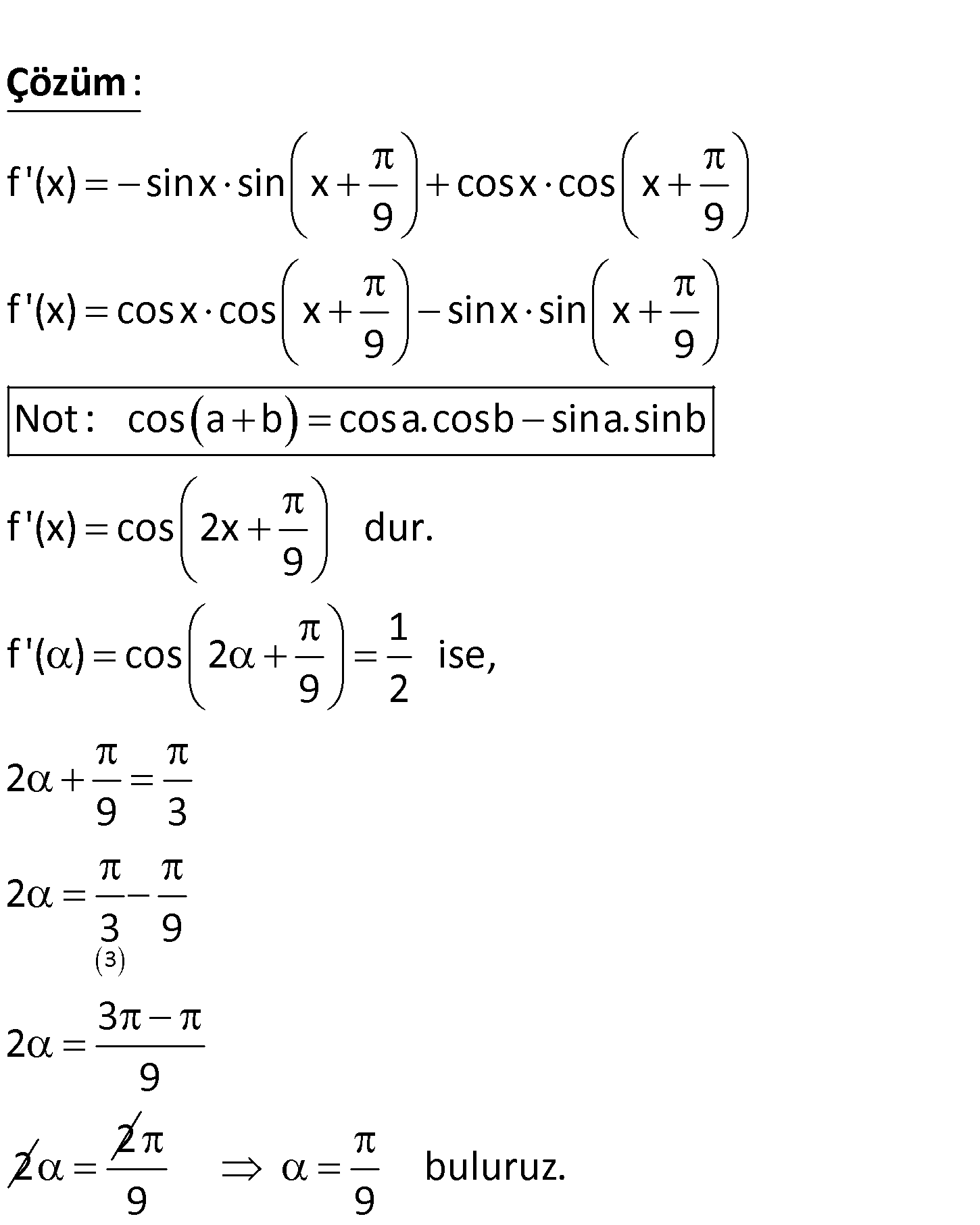
7.SORU
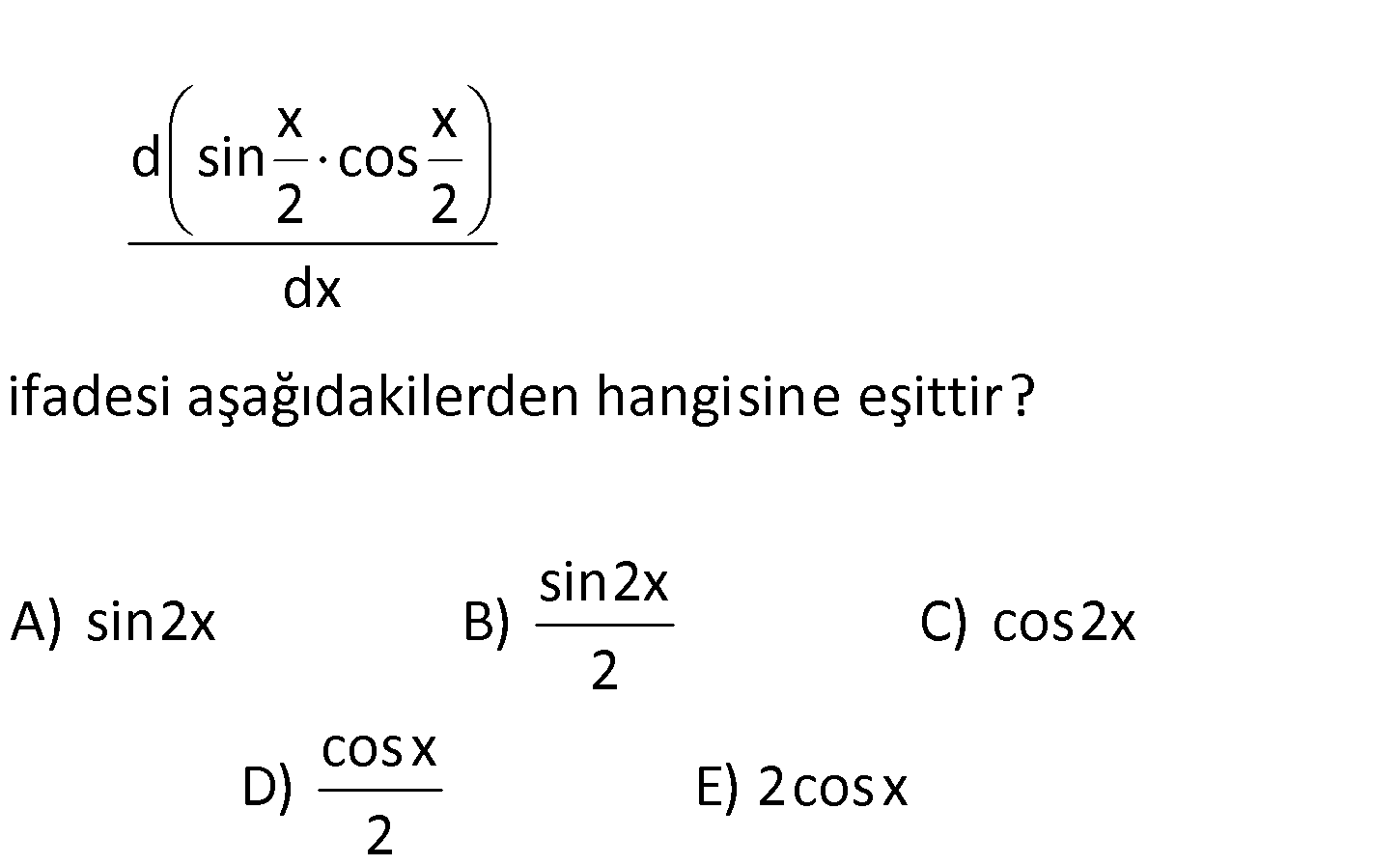
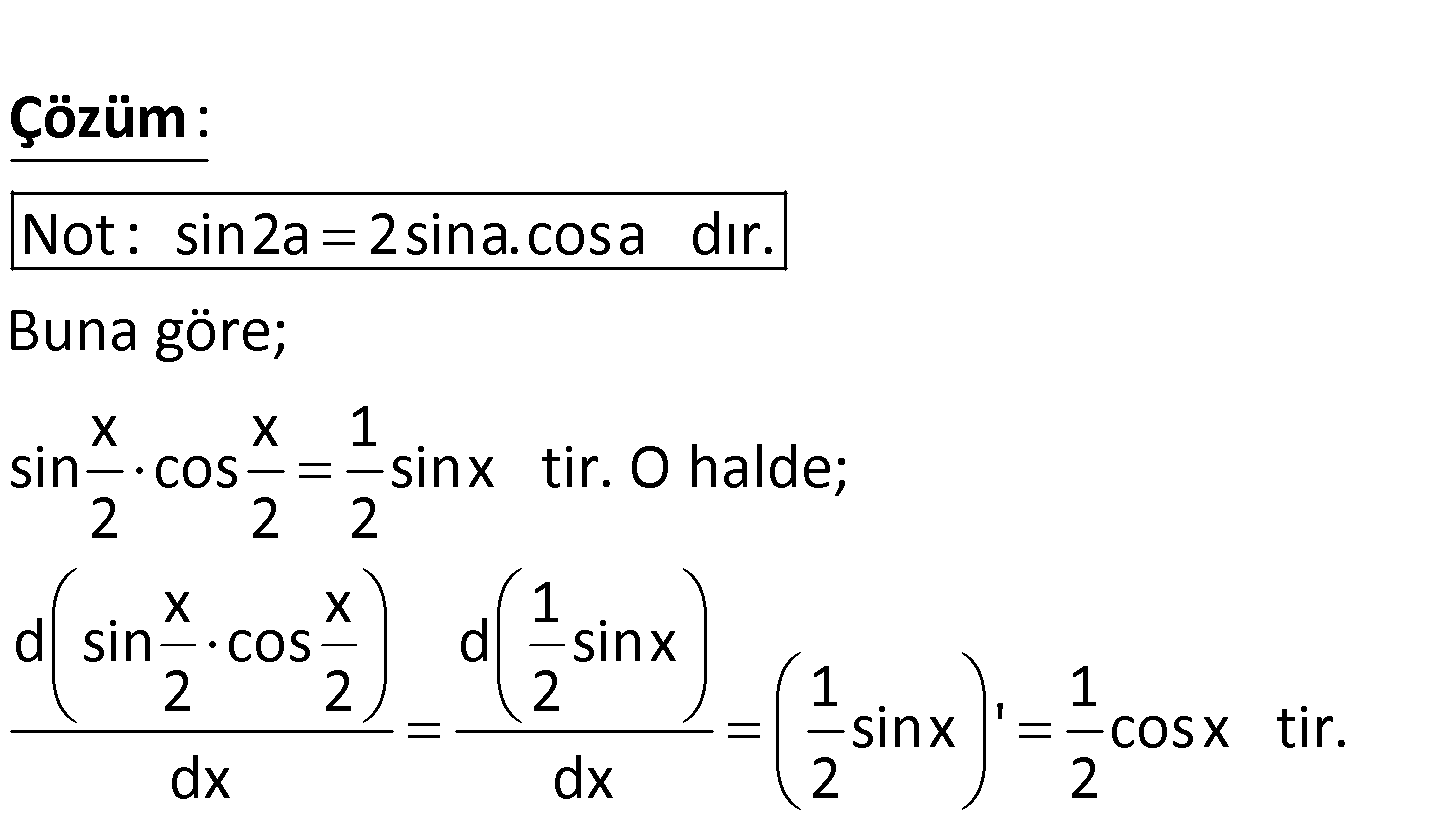
8.SORU
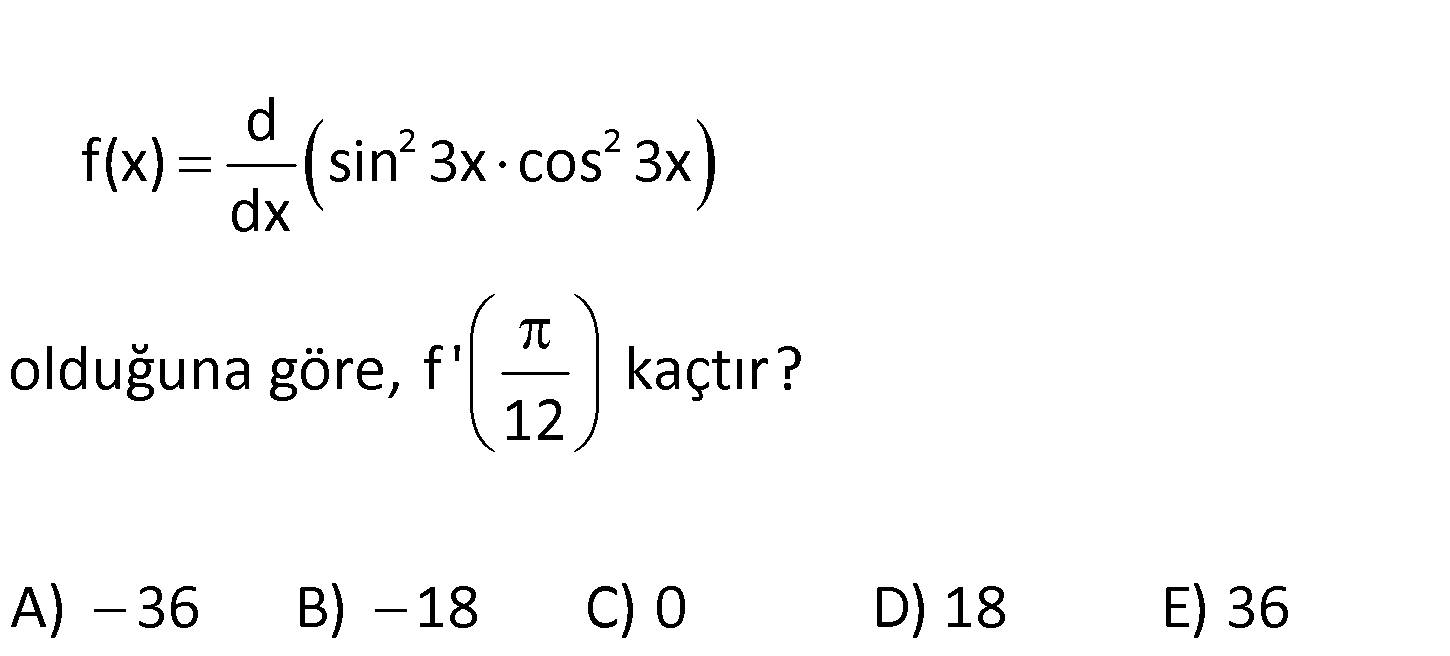
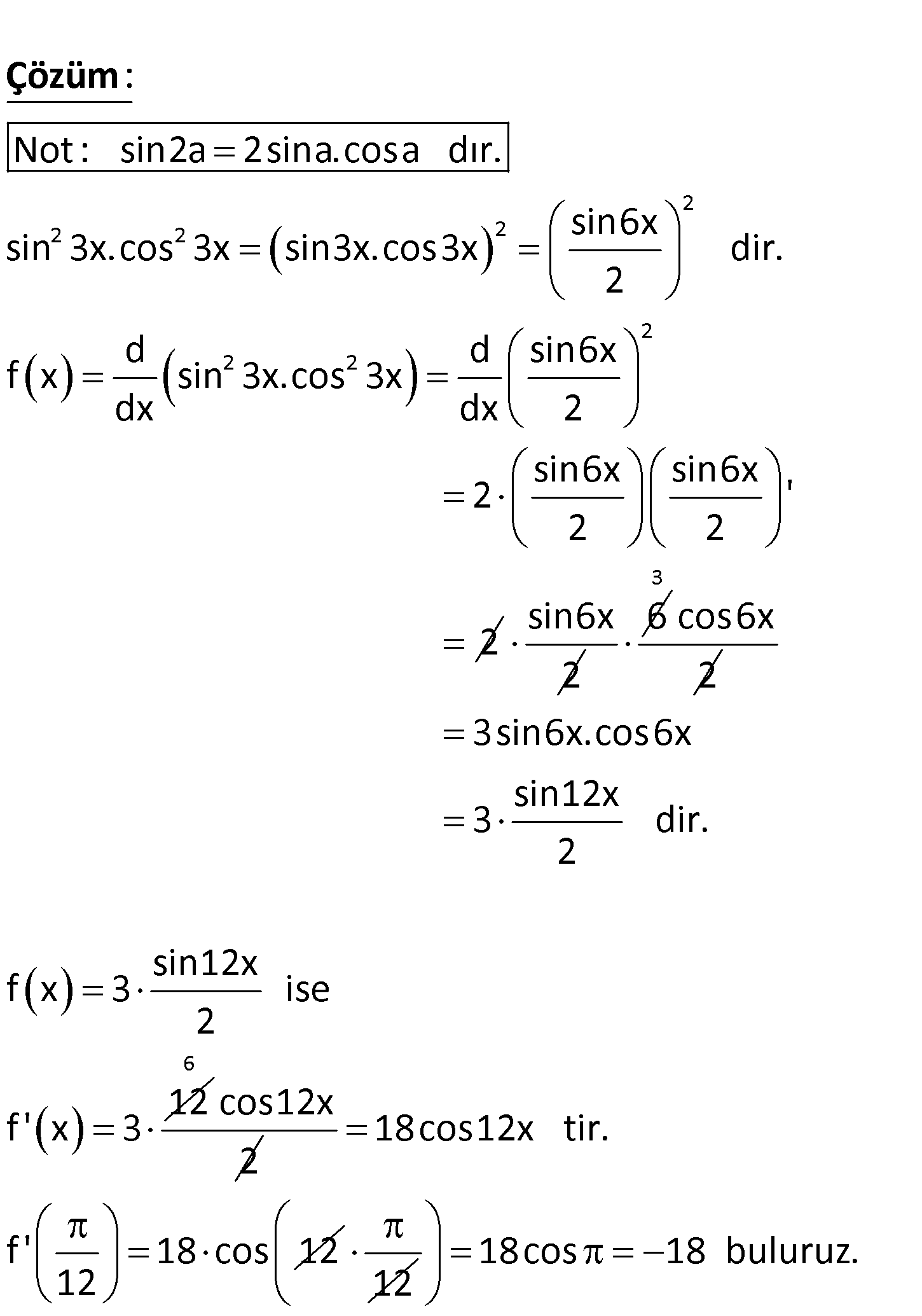
9.SORU
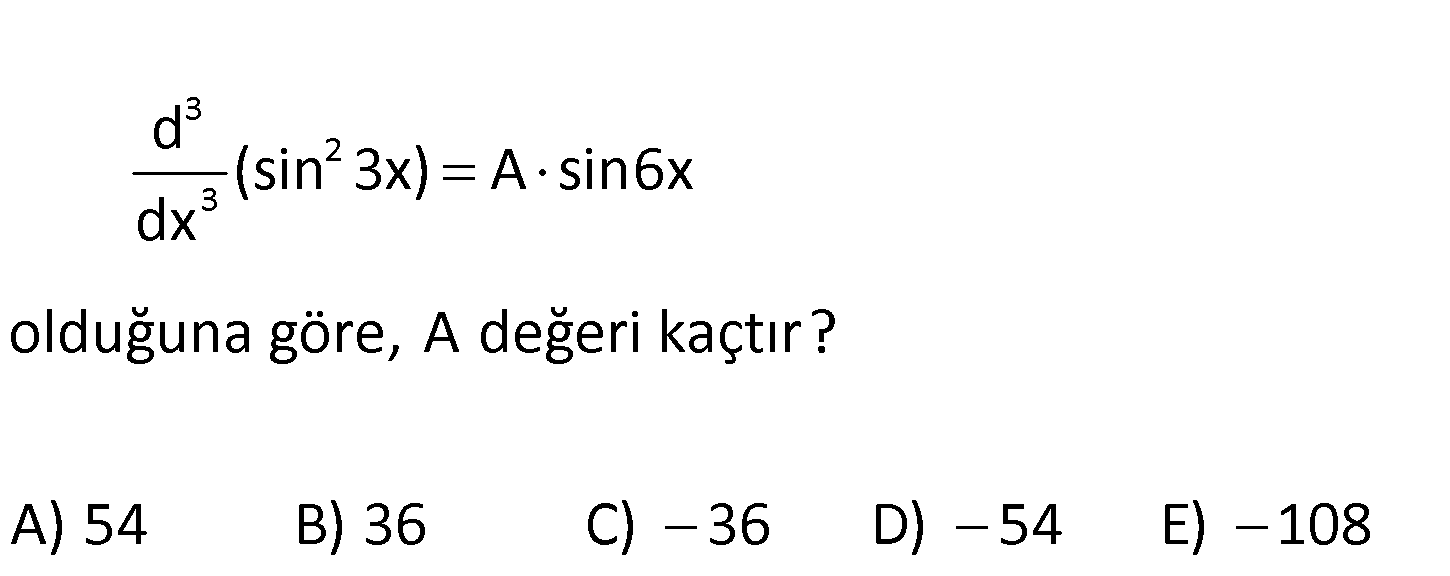

10.SORU
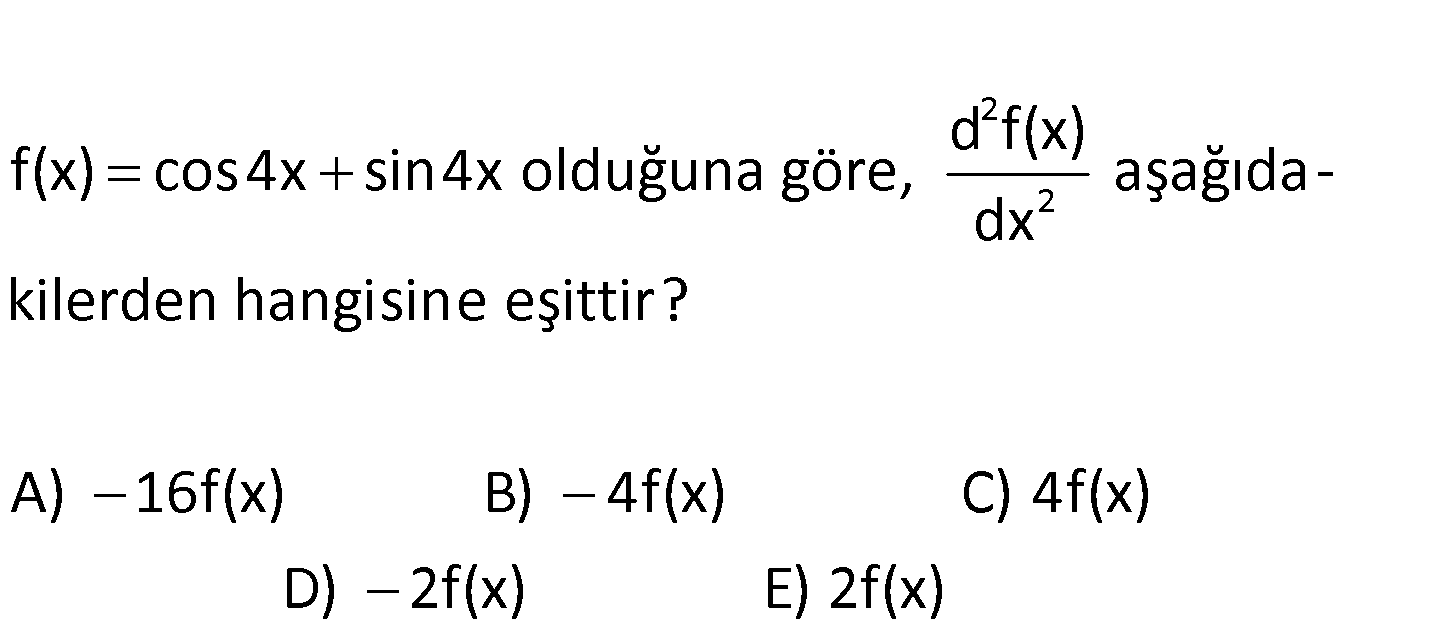

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
Aşağıdaki fonksiyonların türevlerini bulunuz. a) 5sinx cosx b) 2 www.matematikkolay.net Sinüs ve Kosinüs Fonksiyonunun Türevi (sinx )’ cosx (cosx)’ sinx a) (5sinx)’ 5cos : x Çözüm tir. cosx 1 b) ‘ sinx tir. 2 2 184
2 2 f(x) 5cos x.sin x olduğuna göre, f ‘(x) aşağıdakilerden hangisine eşit – tir? A) sin2x B) cos2x C) 2cos2x D) 2sin4x E) cos4x 2 2 2 2 sin2x 2 f(x) 4cos x.sin x (2sinx.cosx) sin 2x dir. f'(x)=(sin 2x)’ 2sin2x.(sin2x)’ 2sin2 : Çözüm sin4x x.2.cos2x 2.2.sin2x.cos2x 2sin4x buluruz. www.matematikkolay.net 18
2 3 2 f(x) sin x cos x cos x olduğuna göre, f ‘ değeri kaçtır? 6 1 3 7 9 A) B) C) D) E) 2 4 8 8 2 www.matematikkolay.net 2 3 2 2 2 3 3 2 2 f(x) sin x cos x cos x f(x) sin x cos x cos x f(x) 1 cos x f ‘(x) 3cos x.(cosx)’ f ‘(x) 3cos x.( s : Çözüm 2 2 inx) f ‘ 3cos .sin 6 6 6 3 1 3 1 9 3 . 3 . buluruz. 2 2 4 2 8 34
f(x) cos sinx 3 olduğuna göre, f ‘ değeri kaçtır? 6 3 3 3 3 3 A) – B) – C) – D) – E) – 12 4 2 12 8 www.matematikkolay.net ı ı f(x) cos sinx f (x) cosx.sin sinx 3 3 3 f cos sin sin 6 3 6 3 6 : Çözüm 6 3 1 3 1 3 sin bulunur. 3 2 3 2 3 2 2 12 80
f(x) 3sin2x.cos2x olduğuna göre, f ‘ ifadesinin değeri kaçtır? 3 A) -3 3 B) -6 C) -3 D) – 3 E) 3 3 Not : sin2a 2sina.cosa Bunu kullanarak; f(x) 3sin2x.cos2x sin4x 3 olarak yazabiliriz. 2 : T Çözüm ürevi; 3 f ‘(x) 2 4 2 3.bölgede kosinüs dir. cos4x 6cos4x olur. f ‘ 6cos 4 6cos 4.60 6 cos240 3 3 6 cos 180 60 6cos60 1 6 3 buluruz. 2 110
1 f ‘ 2 olduğuna göre, aşağıdakilerden hangisi f(x) cosx sinx olabilir? A) B) C) D) 18 9 x 9 6 E) 4 3 www.matematikkolay.net f ‘(x) sinx sin x cosx cos x 9 9 f ‘(x) cosx cos x sinx sin x 9 9 No : t : Çözüm 3 cos a b cosa.cosb sina.sinb f ‘(x) cos 2x dur. 9 1 f ‘( ) cos 2 ise, 9 2 2 9 3 2 3 9 3 2 9 2 2 buluruz. 9 9 124
ifadesi aşağıdakilerden hangisine eşittir? x x d sin cos 2 2 sin2x A) sin2x B) C) dx cos2x 2 cosx D) E) 2cosx 2 Not : sin2a 2sina.cosa dır. Buna göre; x x 1 sin cos sinx tir. O halde; 2 2 2 x x d sin cos 2 2 d : x Çözüm 1 d sinx 2 1 1 sinx ‘ cosx tir. dx 2 2 127
2 2 olduğuna göre, f ‘ kaçtır? 12 A) d f(x) sin 3x cos 3x 36 B) 18 C) 0 D) 18 E) 36 dx www.matematikkolay.net 2 2 2 2 2 Not : sin2a 2sina.cosa dır. sin6x sin 3x.cos 3x sin3x.cos3x dir. 2 d f x sin 3x : .cos dx Çözüm 2 2 d sin6x 3x dx 2 sin6x sin6x 2 ‘ 2 2 2 sin6x 2 6 3 cos6x 2 3sin6x.cos6x sin12x 3 dir. 2 sin12x f x 3 ise 2 12 f ‘ x 3 6 cos12x 2 18cos12x tir. f ‘ 18 cos 12 12 12 18cos 18 buluruz. 135
www.matematikkolay.net 3 2 3 d (sin 3x) A sin6x dx olduğuna göre, A değeri kaçtır? A) 54 B) 36 C) 36 D) 54 E) 108 2 sin 3x ‘ 2sin3x.3.cos3x 3.sin6x tir. Tekrar türev alalım. 3sin6x ‘ 18cos6x tir. Tekrar türev : Çözüm 2 alalım. 18cos6x ‘ 108sin6x tir. sin 3x in 3.türevi 108sin6x olduğundan; 108 sin6x A sin6x A 108 buluruz. 141
www.matematikkolay.net 2 2 d f(x) f(x) cos4x sin4x olduğuna göre, aşağıda – dx kilerden hangisine eşittir? A) 16f(x) B) 4f(x) C) 4f(x) D) 2f(x) E) 2f(x) 2 2 d f(x) ifadesi bizden iki defa türev almamızı istiyor. dx f(x) cos4x sin4x f ‘(x) 4sin4x 4co : Çözüm f(x) s4x 4 sin4x cos4x olur. f ”(x) 4 4cos4x 4sin4x 4 4 cos4x sin4x 16 cos4x sin4x 16f(x) buluruz.

