Soru Sor sayfası kullanılarak Türev konusu altında Çarpımın Türevi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
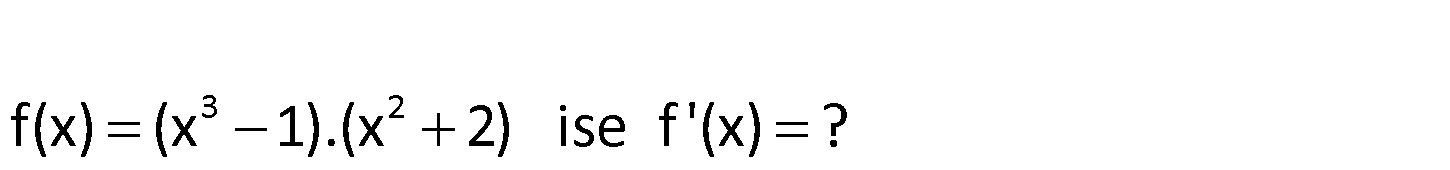

2.SORU

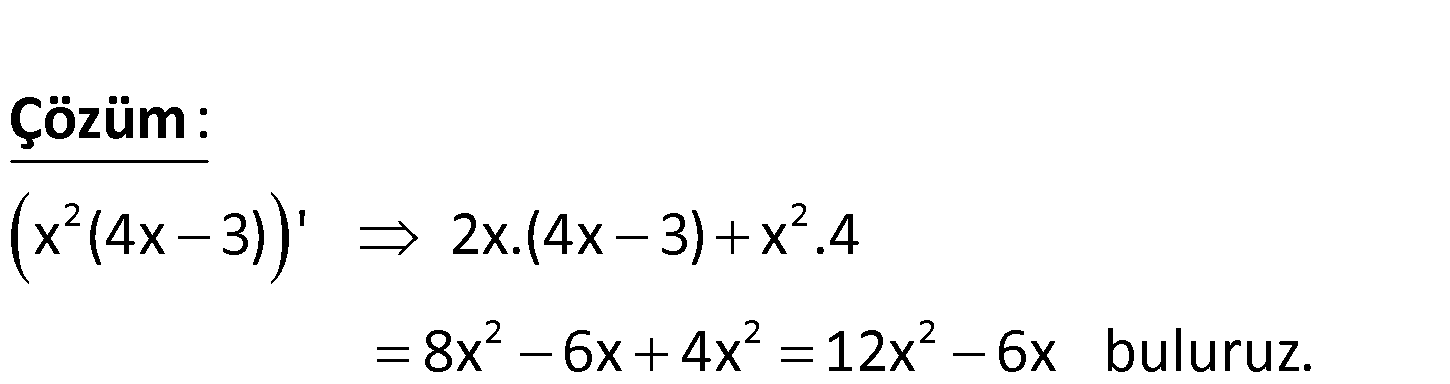
3.SORU
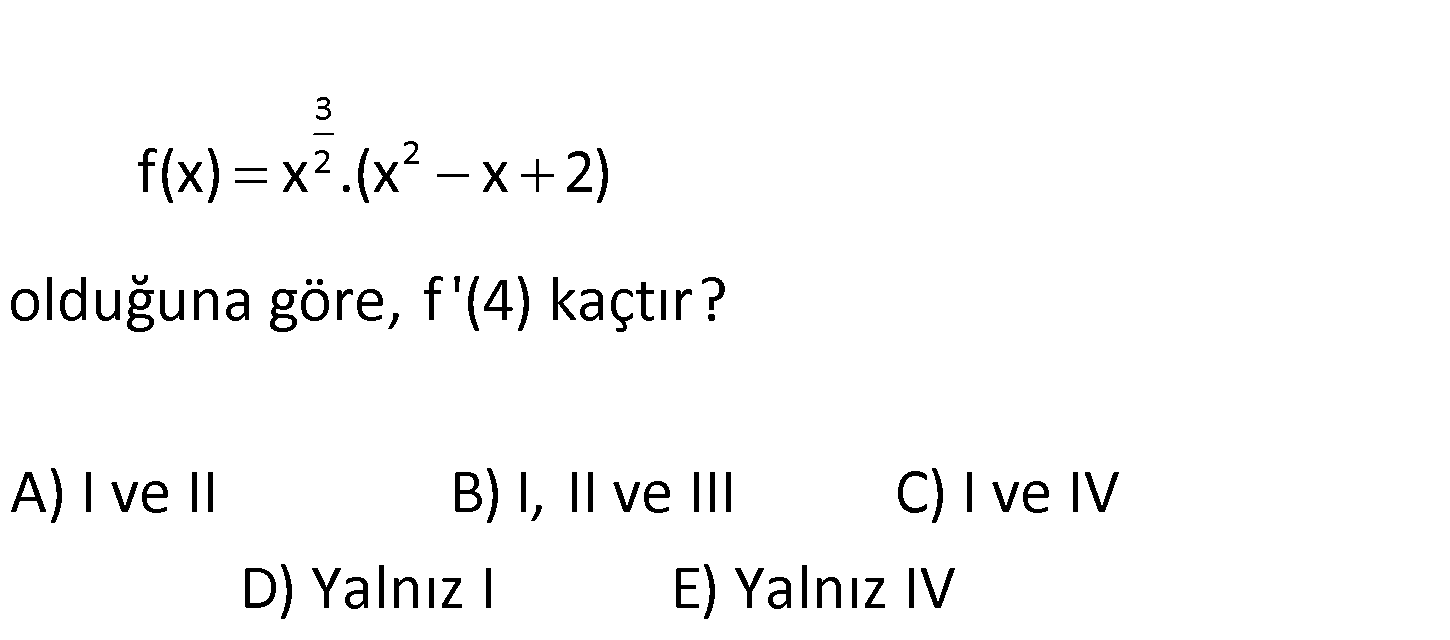
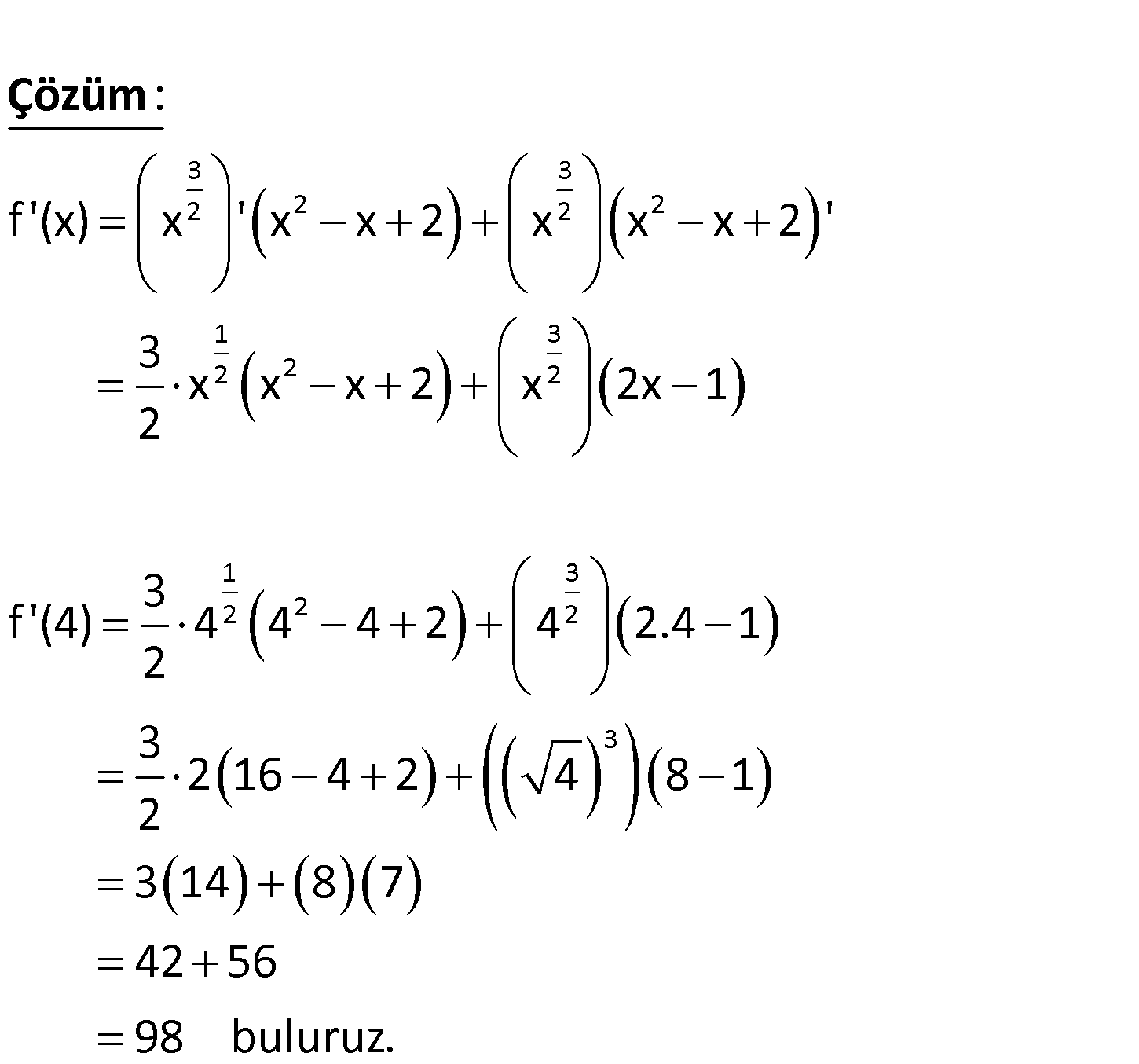
4.SORU
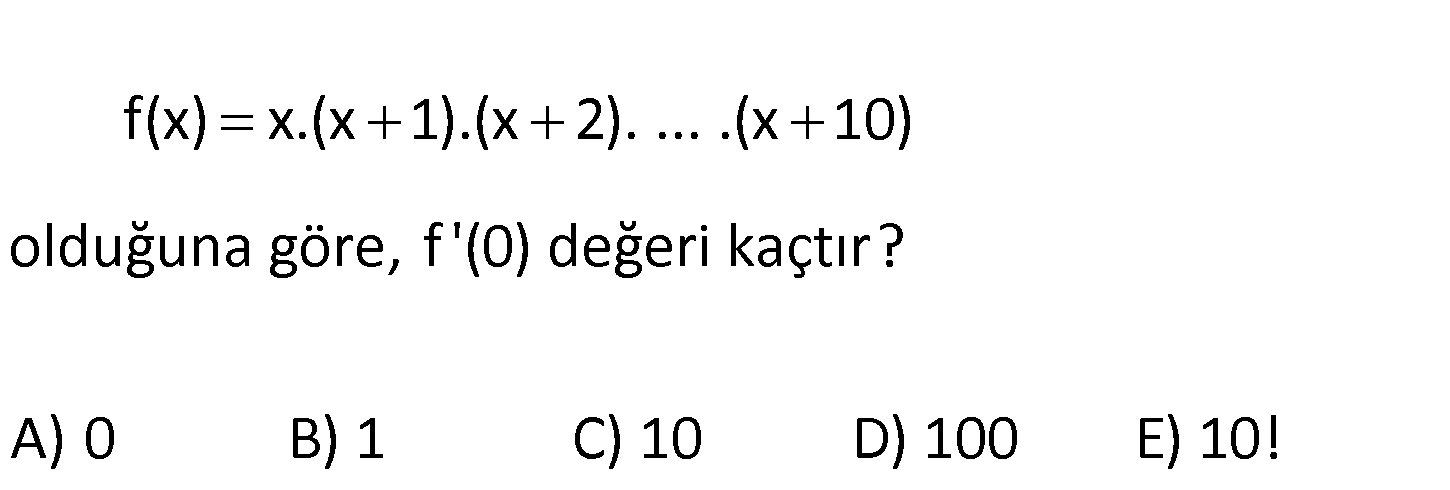

5.SORU


6.SORU


7.SORU

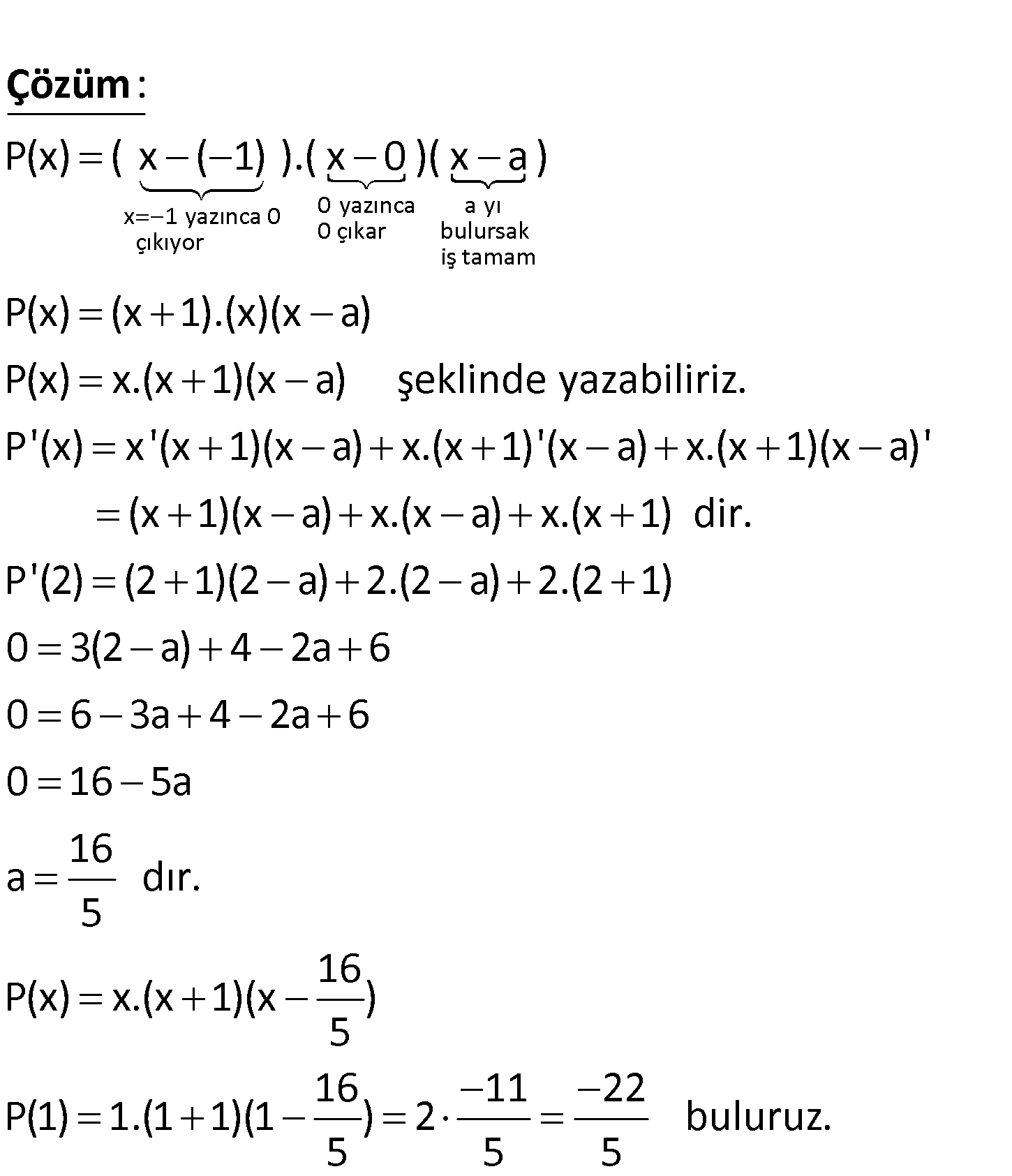
Burdan sonraki sorular, Fen Lisesi Müfredatı için geçerlidir.
8.SORU
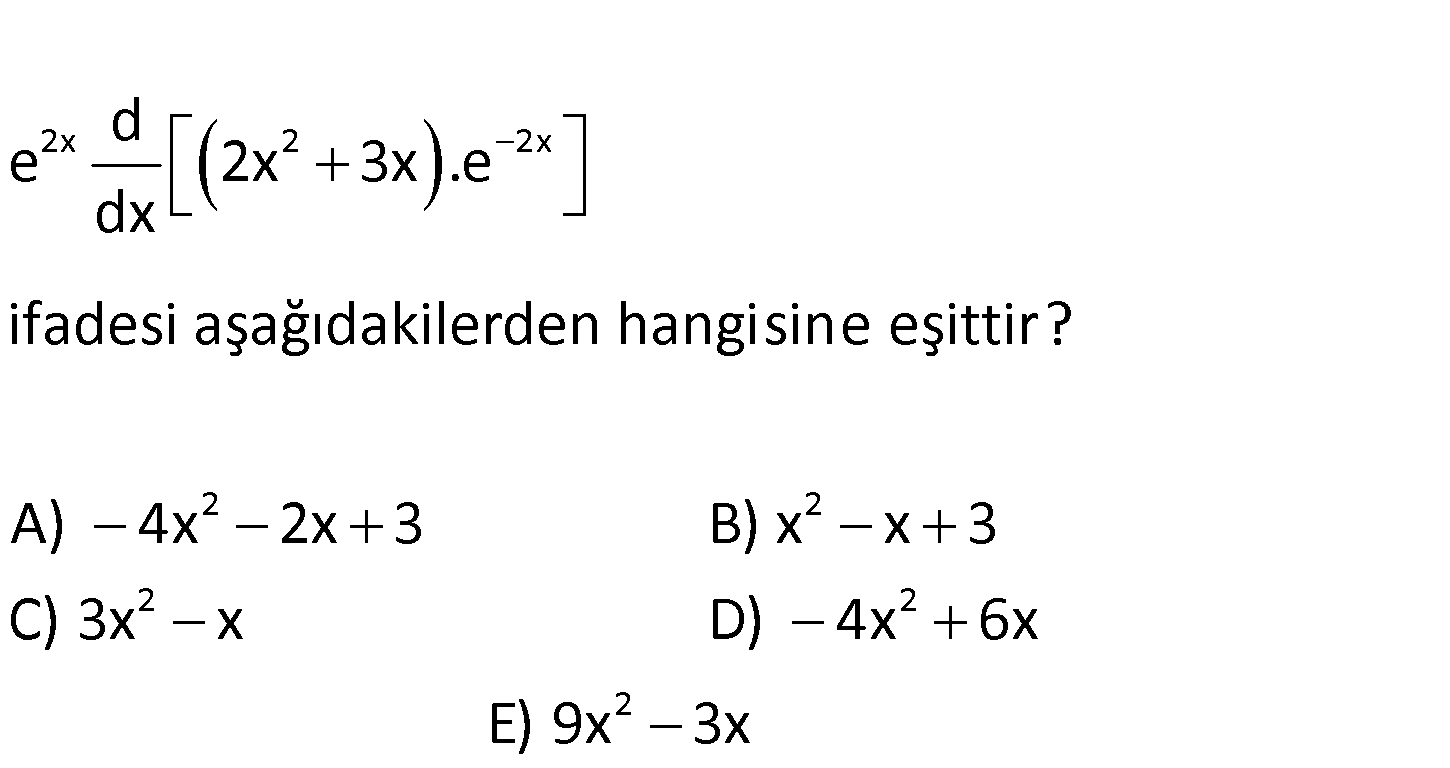
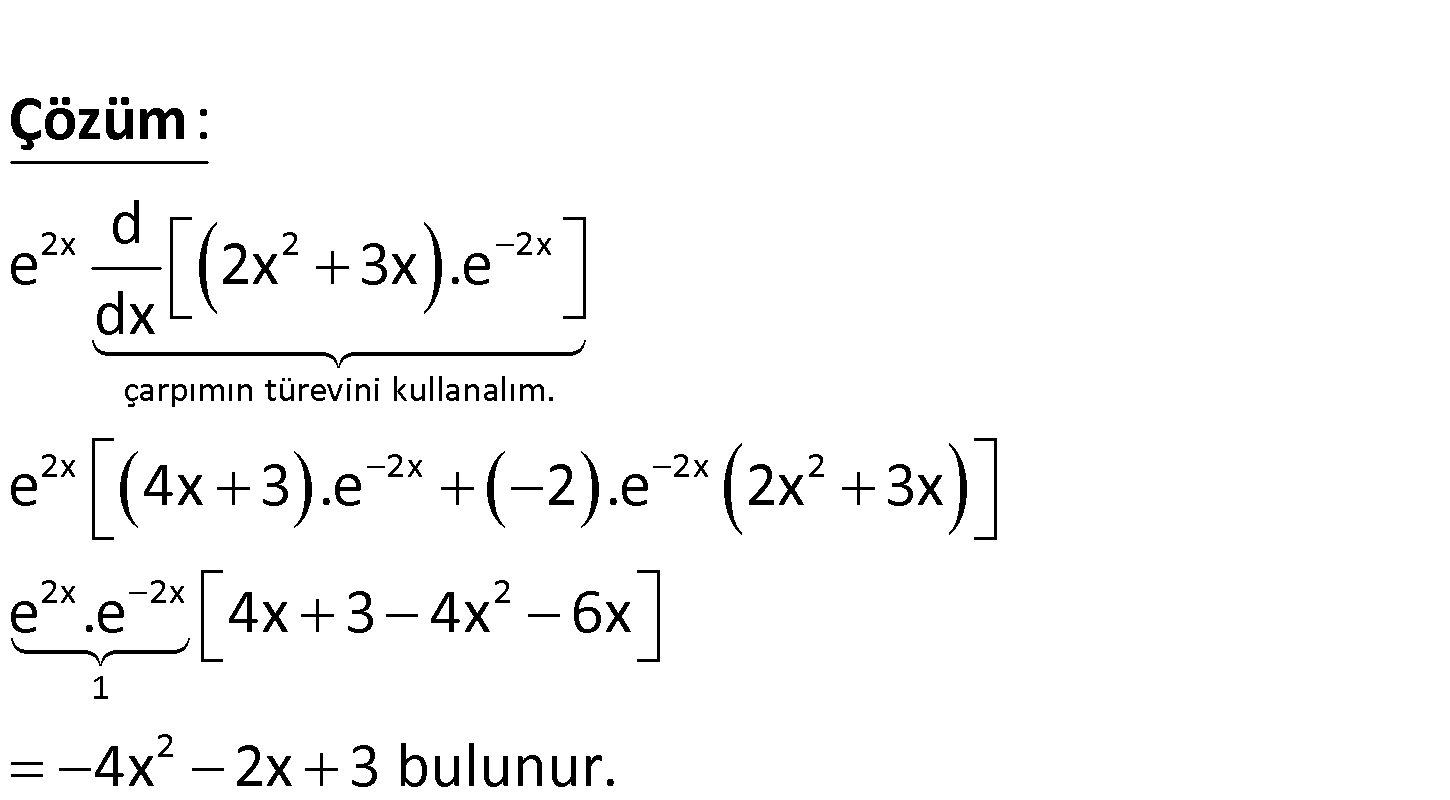
9.SORU
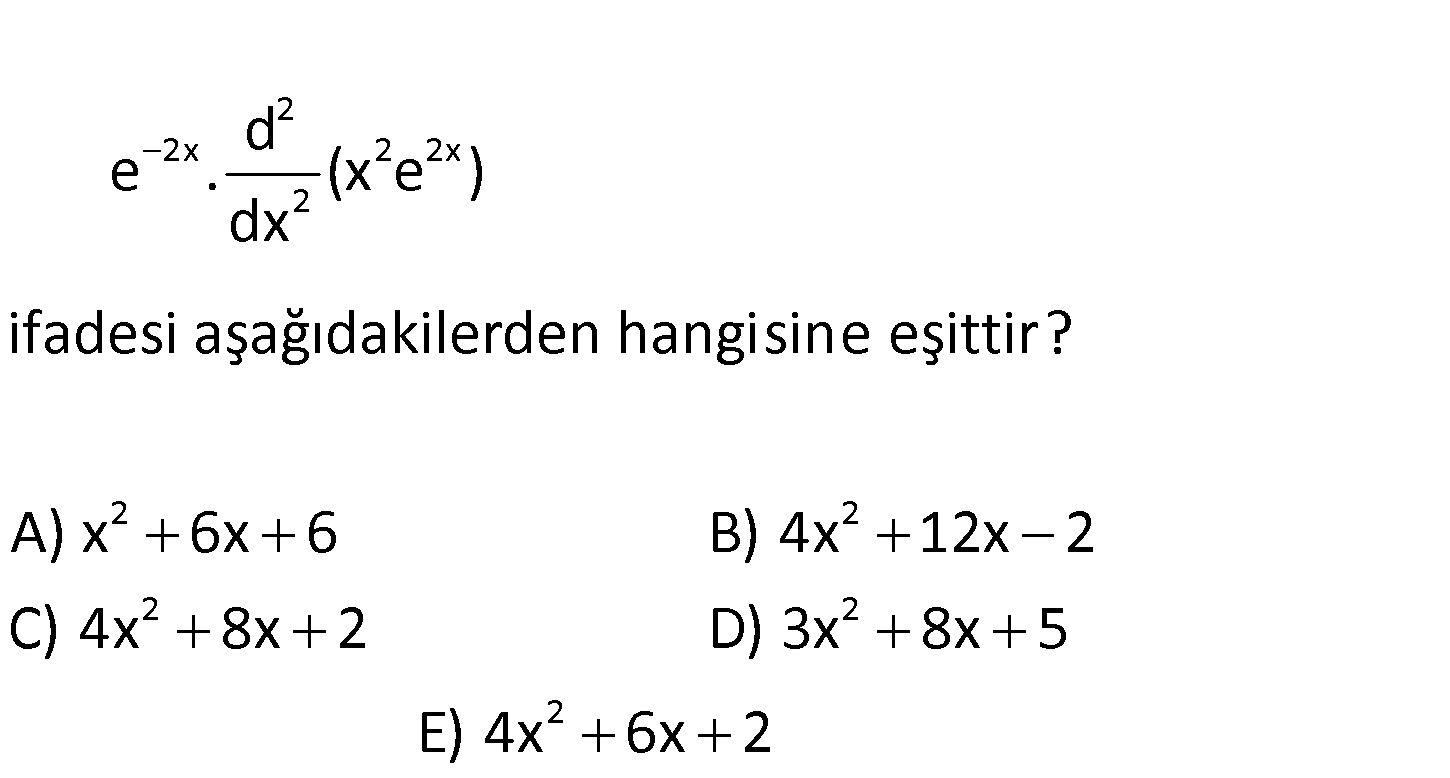
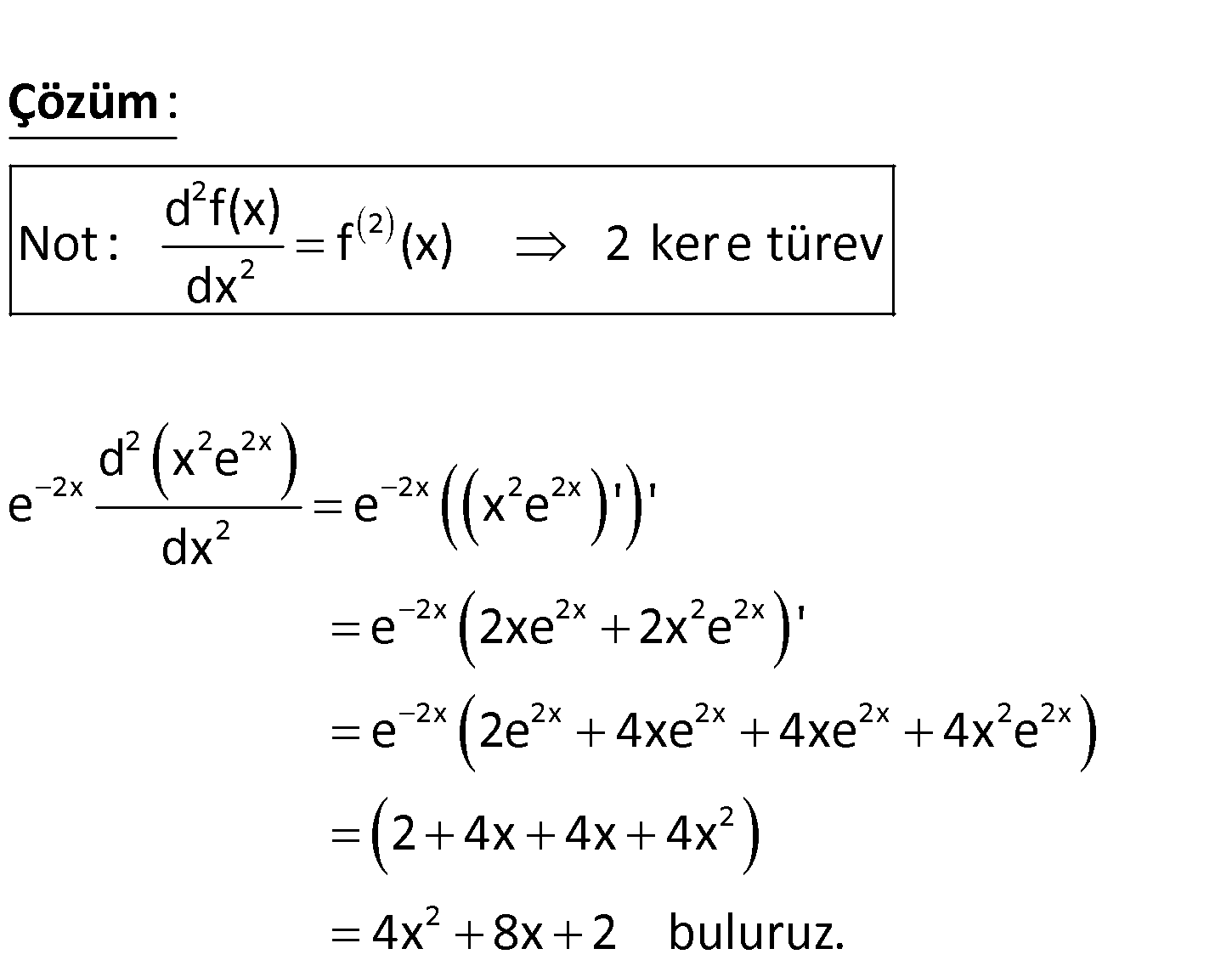
10.SORU
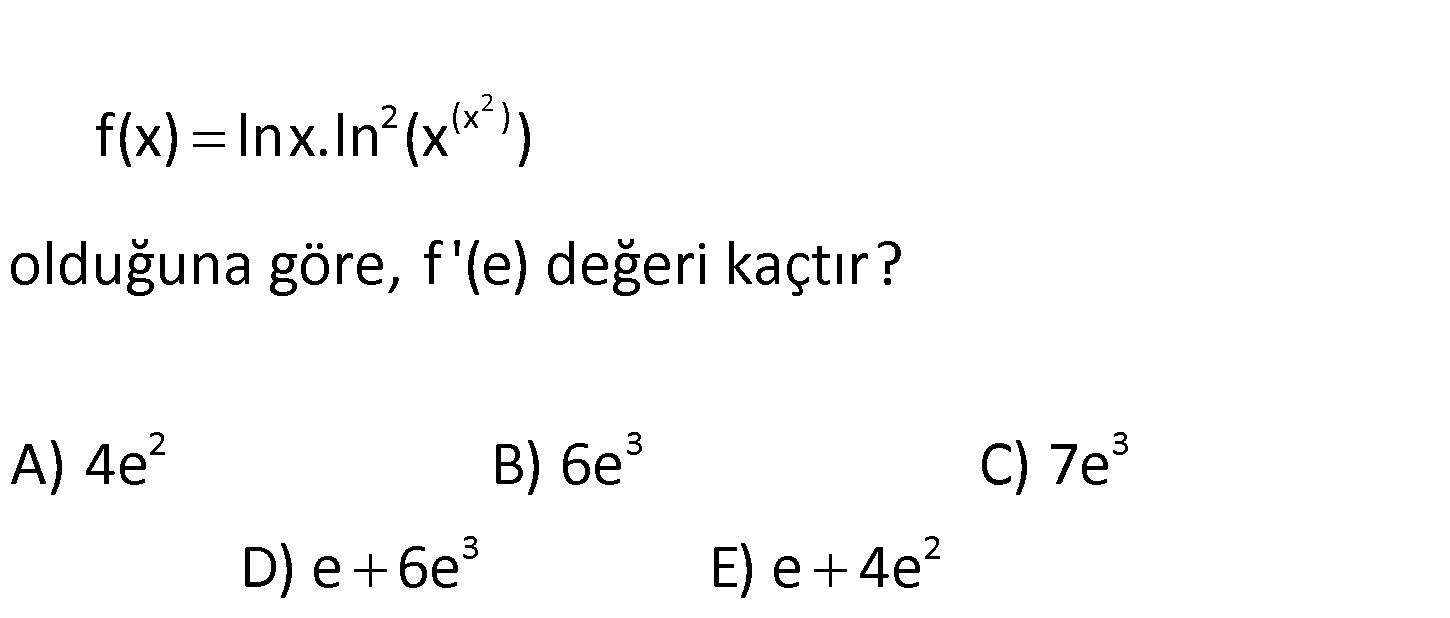

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3 2 f(x) (x 1).(x 2) ise f ‘(x) ? www.matematikkolay.net 3 2 Çarpımın Türevi f(x).g(x) in türevi f ‘(x).g(x) f(x).g'(x) tir. f(x) x 1 x 2 f ‘ ) : (x Çözüm 2 2 3 4 2 4 4 2 3x x 2 x 1 2x f ‘(x) 3x 6x 2x 2x f ‘(x) 5x 6x 2x buluruz. 177
www.matematikkolay.net 2 y x (4x 3) ise y’ ? 2 2 2 2 2 x (4x 3) ‘ 2x.(4x 3) x .4 8x 6x 4x 12x 6x bulu u : r z. Çözüm 93
3 2 2 f(x) x .(x x 2) olduğuna göre, f ‘(4) kaçt A) I ve II B) I, II ve III C) I ve IV ır? D) Yalnız I E) Yalnız IV www.matematikkolay.net 3 3 2 2 2 2 1 3 2 2 2 1 2 2 f ‘(x) x ‘ x x 2 x x x 2 ‘ 3 x x x 2 x 2x 1 2 3 f ‘(4) 4 4 : 4 2 2 Çözüm 3 2 3 4 2.4 1 3 2 16 4 2 4 8 1 2 3 14 8 7 42 56 98 buluruz. 108
f(x) x.(x 1).(x 2). … .(x 10) olduğuna göre, f ‘(0) değeri kaçtır? A) 0 B) 1 C) 10 D) 100 E) 10 ! f(x) x.(x 1).(x 2)…(x 10) Türev alınınca her bir çarpanın türevi alınıp, geri kalan kısım a : Çözüm ynen yazılır. f ‘(x) x’.(x 1)..(x 10) x.(x 1)’..(x 10) … x.(x 1)..(x 10)’ f ‘(x) 1.(x 1)..(x 10) x.(1)..(x 10) … x.(x 1)..(1) f ‘(0) 1.(0 1)..(0 10) 0 0.(1)..(0 10) … 0.(0 1)..(1) f ‘(0) 1.1.2.3….10 f ‘(0) 10! buluruz. www.matematikkolay.net 35
3 Türevlenebilir bir f(x) fonksiyonu için f(1) 2 ve f ‘(1) 1 olduğuna göre, x.f (x) fonksi yonunun x 1 noktasındaki türevi kaçtır? A) 20 B) 18 C) 12 D) 11 E) 8 3 3 3 3 2 3 (x.f (x))’ 1.f (x) x.(f (x))’ f (x) x.3f (x).f ‘(x) dir. x 1 için : f (x) x Çözüm 2 3 2 3 2 .3f (x).f ‘(x) f (1) 1.3f (1).f ‘(1) 2 3.2 .1 8 3.4 8 12 20 buluruz. 16
www.matematikkolay.net f(x) (x 1)(x 2)…(x 8) ise f ‘(7) ? f x x 1 x 2 … x 8 Çarpanların türevi sırasıyla alınacak. f ‘ x 1. x 2 … x 8 x 1 .1…. x 8 : Çözüm ….. x 1 x 2 …1 olur. Bu toplanan terimlerde x 7 çarpan olarak bulunduğundan, x 7 yazıldığında hep 0 olacak. Bir terim hariç f ‘ 7 1. x 2 … x 8 0 x 1 .1…. x 8 0 ….. 0 x 1 x 2 x 3 x 4 x 5 x 6 1. x 8 x 1 x 2 …1 0 f ‘ 7 0 x 1 x 2 x 3 x 4 x 5 x 6 .1. x 8 f ‘ 7 0 6.5.4.3. 2.1.1. 1 f ‘ 7 6! 720 buluruz. 140
Baş katsayısı 1 olan üçüncü dereceden bir P(x) poli – nomunun türevi P'(x) ve P(1) P(0) P'(2) 0 olduğuna göre, P(1) kaçtır? 22 12 16 A) B) C) 4 D) E) 3 5 5 5 x 1 yazınca 0 0 yazınca a yı çıkıyor 0 çıkar bulursak iş tamam P(x) ( x ( 1) ).( x 0 )( x a ) : Çözüm P(x) (x 1).(x)(x a) P(x) x.(x 1)(x a) şeklinde yazabiliriz. P'(x) x'(x 1)(x a) x.(x 1)'(x a) x.(x 1)(x a)’ (x 1)(x a) x.(x a) x.(x 1) dir. P'(2) (2 1)(2 a) 2.(2 a) 2.(2 1) 0 3(2 a) 4 2a 6 0 6 3a 4 2a 6 0 16 5a 16 a dır. 5 16 P(x) x.(x 1)(x ) 5 16 11 22 P(1) 1.(1 1)(1 ) 2 buluruz. 5 5 5 www.matematikkolay.net 85
2x 2 2x 2 2 2 d e 2x 3x .e dx ifadesi aşağıdakilerden hangisine eşittir? A) 4x 2x 3 B) x x 3 C) 3x x D) 4x 2 2 6x E) 9x 3x 2x 2 2x çarpımın türevini kullanalım. 2x 2x 2x 2 2x d e 2x 3x .e dx e 4x 3 .e 2 .e 2x 3x e : Çözüm 2x 2 1 2 .e 4x 3 4x 6x 4x 2x 3 bulunur. 115
2 2x 2 2 2 2 2x 2 ifadesi aşağıdakilerden hangisine eşittir? A) x 6x 6 B) 4x d e . ( 12x 2 C) 4x 8 x e dx x ) 2 2 2 D) 3x 8x 5 E) 4x 6x 2 www.matematikkolay.net 2 2 2 2 2 2x 2x 2x 2 2x 2 : d f(x) Not : f (x) 2 kere türev dx d x e e e x e ‘ ‘ dx Çözüm 2x 2x 2 2x 2x 2x 2x 2x 2 2x 2 2 e 2xe 2x e ‘ e 2e 4xe 4xe 4x e 2 4x 4x 4x 4x 8x 2 buluruz. 122
2 2 (x ) 2 3 3 olduğuna göre, f ‘(e) değeri kaçtır? A) 4e B) 6e C) 7e f (x) l nx .ln (x ) D) e 6e3 E) e 4e2 www.matematikkolay.net 2 2 2 2 x Burayı düzenleyelim. 2 2 x x 2 2 4 2 f x lnx. ln x ln x ln x x lnx x ln x : Çözüm 4 2 4 3 4 3 3 3 4 2 3 3 4 2 3 3 3 2 3 3 3 2 dir. Buna göre; f x lnx.x ln x x ln x tir. f x x ln x olur. Şimdi türev alalım. f ‘(x) 4x .ln x x .3ln x. lnx ‘ 1 f ‘(x) 4x .ln x x .3ln x x f ‘(x) 4x .ln x x .3ln x x e yazalım. f ‘(e) 4e .ln e e .3ln e f ‘(e) 3 3 3 4e .1 e .3.1 7e buluruz. 129

