Soru Sor sayfası kullanılarak Trigonometri-2 konusu altında sinüs ile kosinüsün eşit olduğu deklemlerin çözümü, sinx=cosa, sinx=sina, cosx=cosa ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
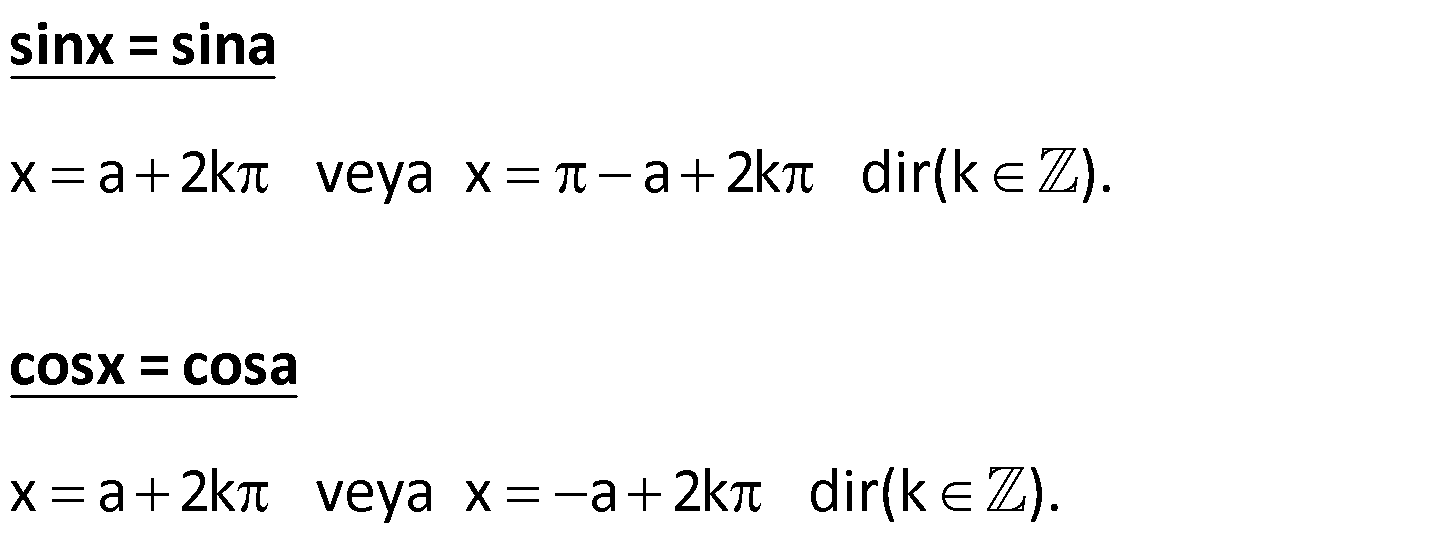
1.SORU
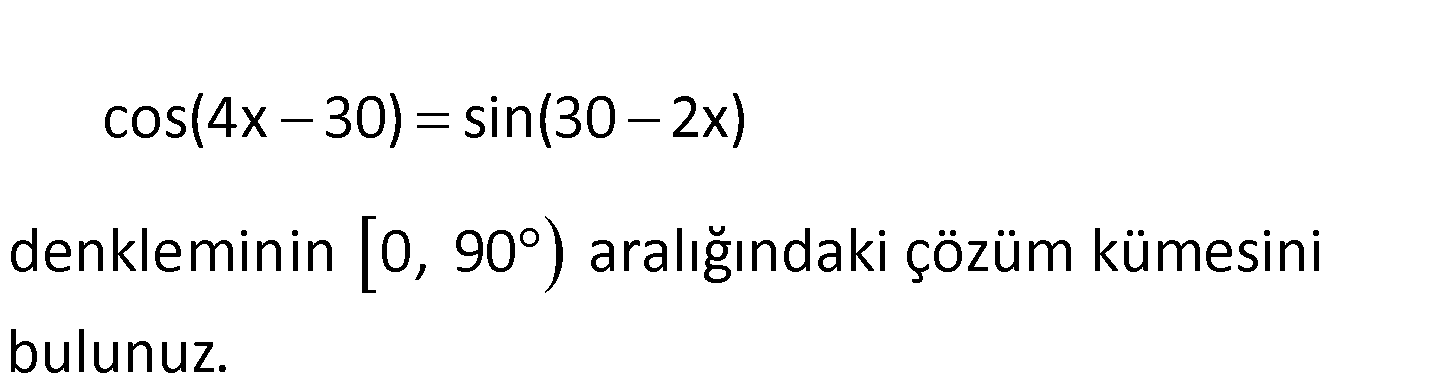

2.SORU
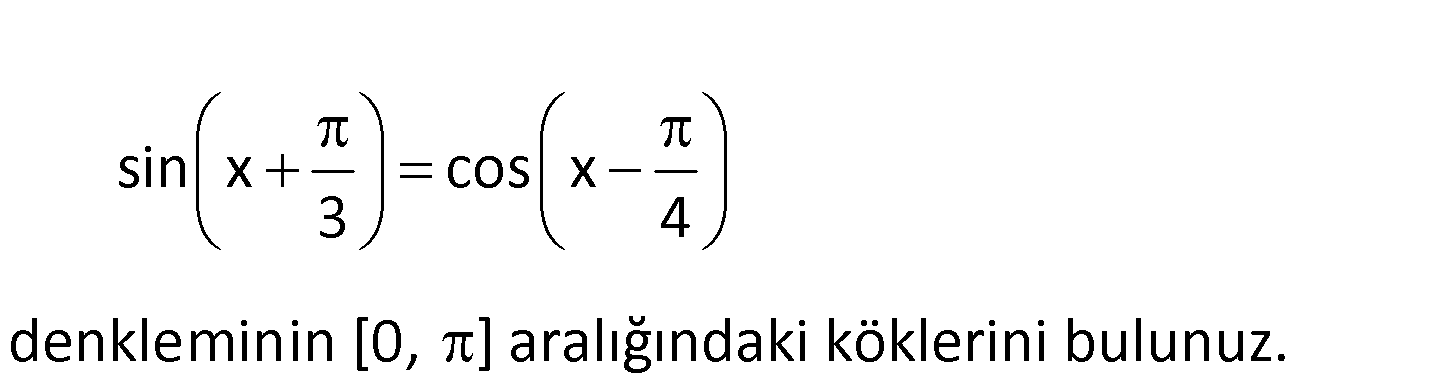
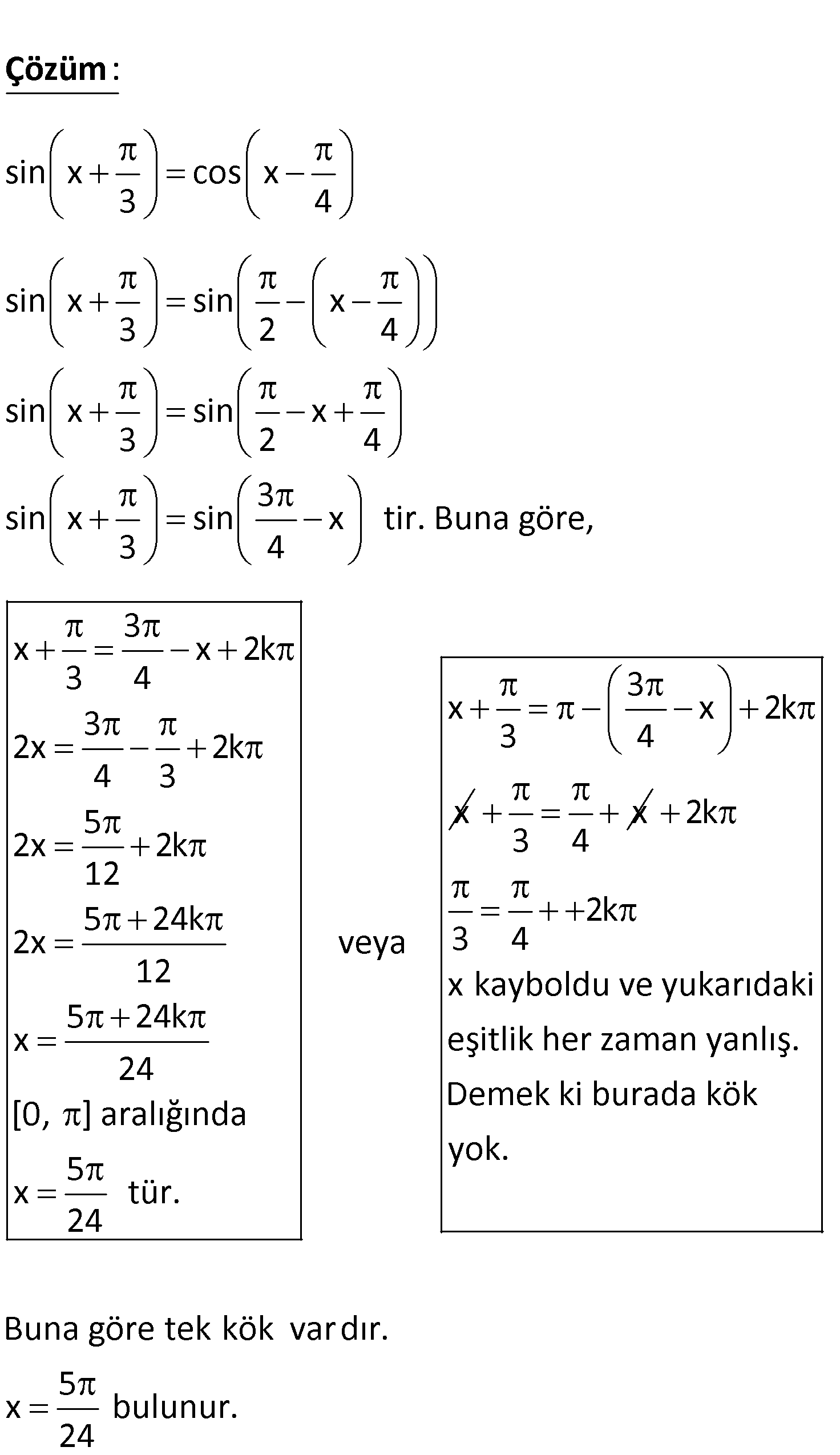
3.SORU

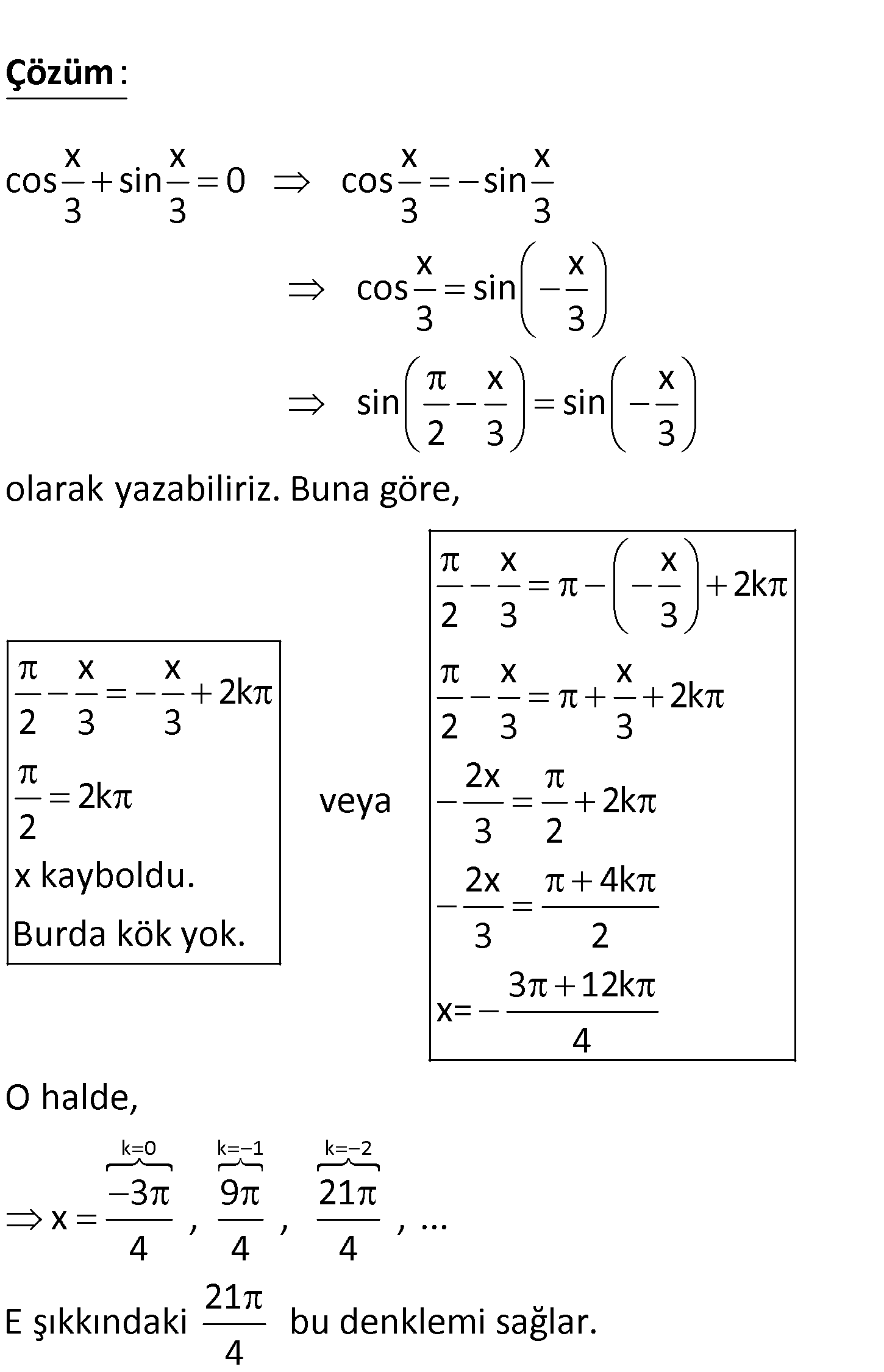
4.SORU

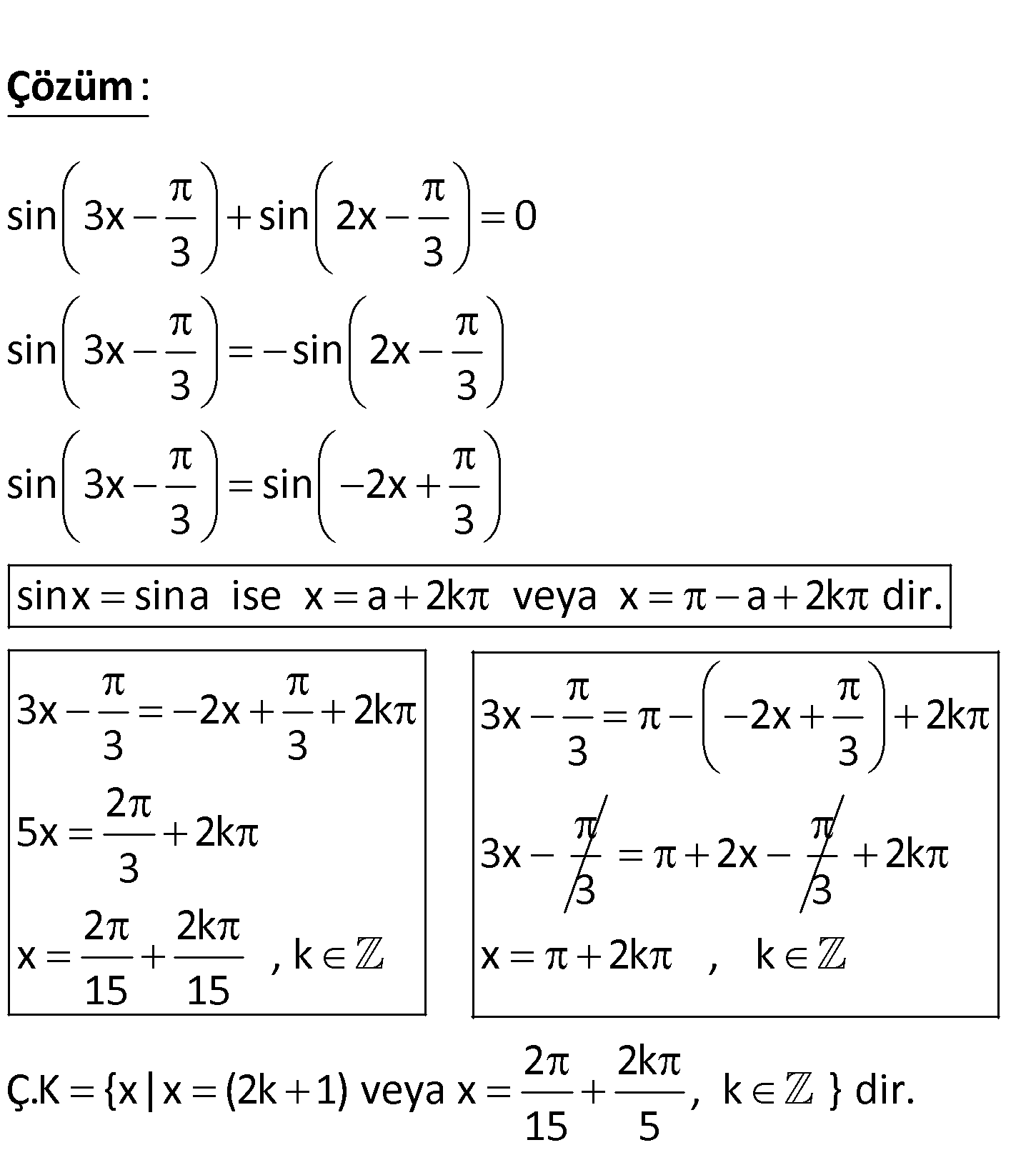
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
cos(4x 30) sin(30 2x) denkleminin 0, 90 aralığındaki çözüm kümesini bulunuz. www.matematikkolay.net cos(4x 30) sin(30 2x) Eşitliğin her iki tarafını aynı trigonometrik ifadeye dönüştürel : im. Mese Çözüm a a la, sin 90 a cosa olduğu için, cos(4x 30) u sin(90 (4x 30)) olarak yazabiliriz. sin(120 4x) olur. Şimdi eşitliği tekrar yazalım. sin(120 4x) sin(30 2x) tir. B una göre, 120 4x 30 2x 360k 120 4x 180 (30 2x) 360k 2x 90 360k 120 4x 150 2x 360k x 45 180k 6x 30 360k [0, 90) aralığında, x 5 60k , [0, 90) aralığında, x 45 dir. x 55 dir. O halde Ç.K={45, 55} dir. 9
sin x cos x 3 4 denkleminin [0, ] aralığındaki köklerini bulunuz. www.matematikkolay.net sin x cos x 3 4 sin x sin x 3 2 4 sin x sin x 3 2 4 : Çözüm 3 sin x sin x tir. Buna göre, 3 4 3 x x 2k 3 4 3 3 x x 2k 2x 2k 3 4 4 3 5 x 2x 2k 12 5 24k 2x veya 12 5 24k x 24 [0, ] aralığında 5 x tür. 24 x 3 4 2k 2k 3 4 x kayboldu ve yukarıdaki eşitlik her zaman yanlış. Demek ki burada kök yok. Buna göre tek kök vardır. 5 x bulunur. 24 18
www.matematikkolay.net x x cos sin 0 3 3 denkleminin köklerinden biri aşağıdakilerden hangisidir? 3 5 A) B) C) D) 4 4 17 21 E) 4 4 x x x x cos sin 0 cos sin 3 3 3 3 x x cos sin 3 3 : Çözüm x x sin sin 2 3 3 olarak yazabiliriz. Buna göre, x x 2k 2 3 3 x x x x 2k 2k 2 3 3 2 3 3 2x 2k veya 2k 2 3 2 x kayboldu. 2x 4k Burda kök yok. 3 2 3 12k x= 4 O k 0 k 1 k 2 halde, 3 9 21 x , , , … 4 4 4 21 E şıkkındaki bu denklemi sağlar. 4 33
sin 3x sin 2x 0 3 3 denkleminin çözüm kümesini bulunuz. www.matematikkolay.net sin 3x sin 2x 0 3 3 sin 3x sin 2x 3 3 sin 3x sin 2x 3 s : 3 Çözüm inx sina ise x a 2k veya x a 2k dir. 3x 2x 2k 3x 2x 2k 3 3 3 3 2 5x 2k 3x 3 3 2 2k x , k 15 15 2x 3 2k x 2k , k 2 2k Ç.K {x|x (2k 1) veya x , k } dir. 15 5 14

