Soru Sor sayfası kullanılarak Trigonometri-2 konusu altında Çarpanlara ayırarak trigonometrik denklem çözme ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
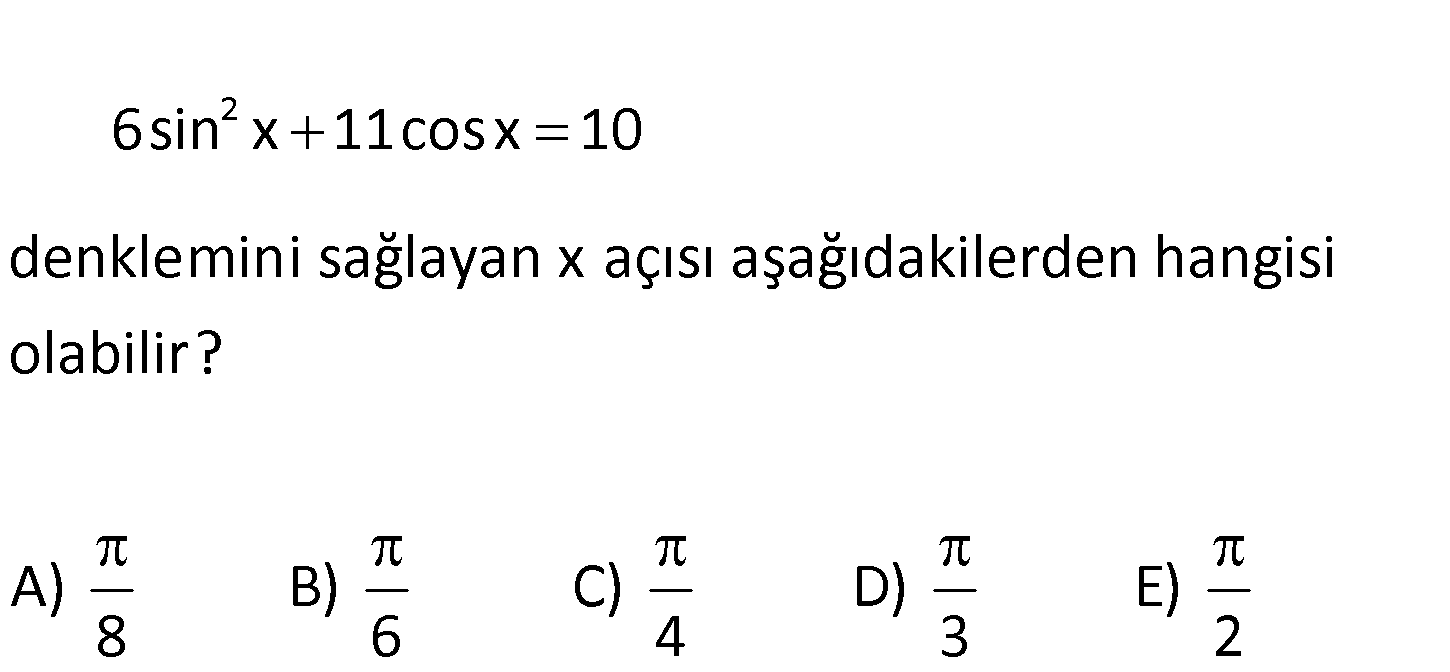

2.SORU
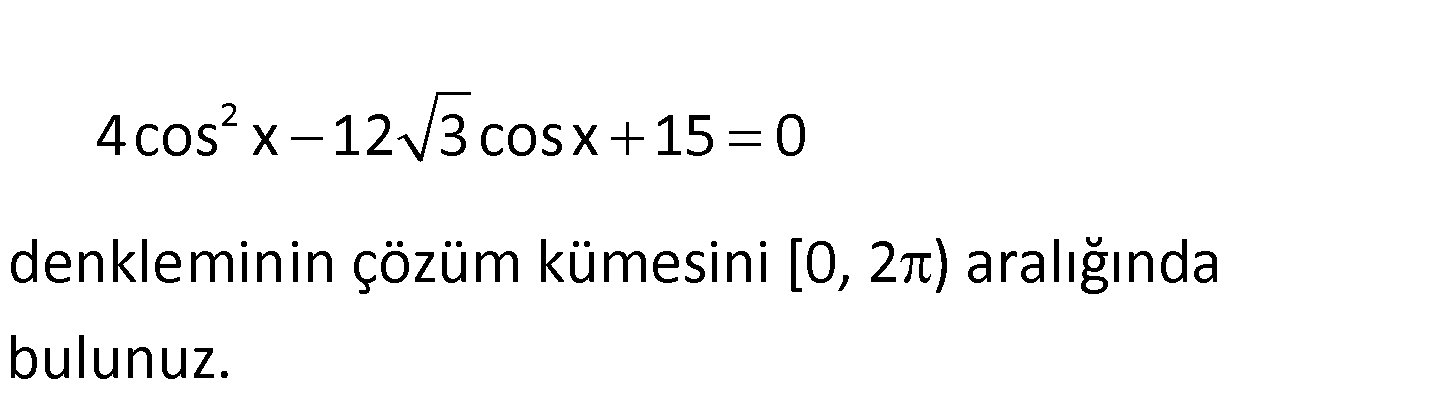

3.SORU
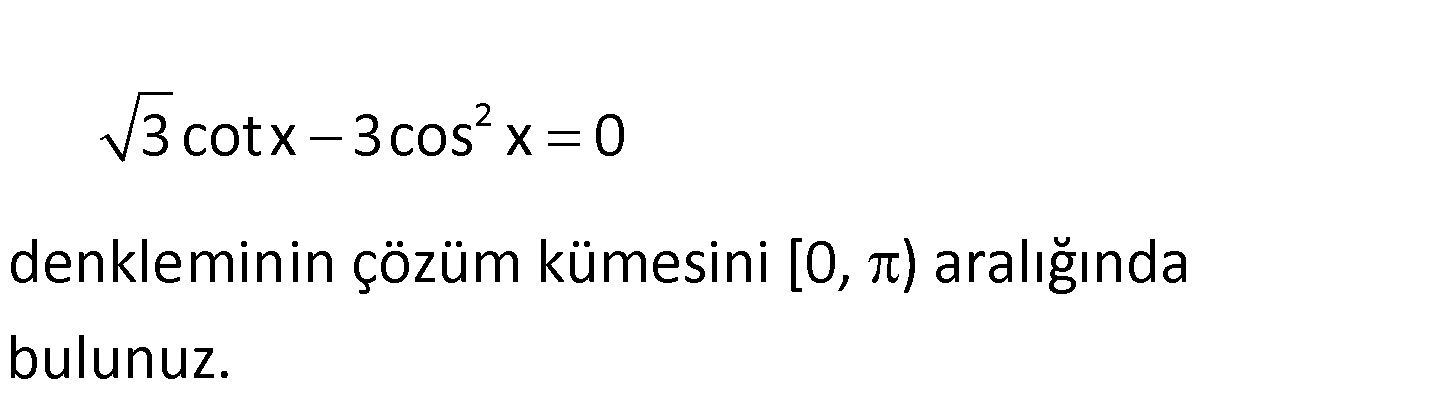
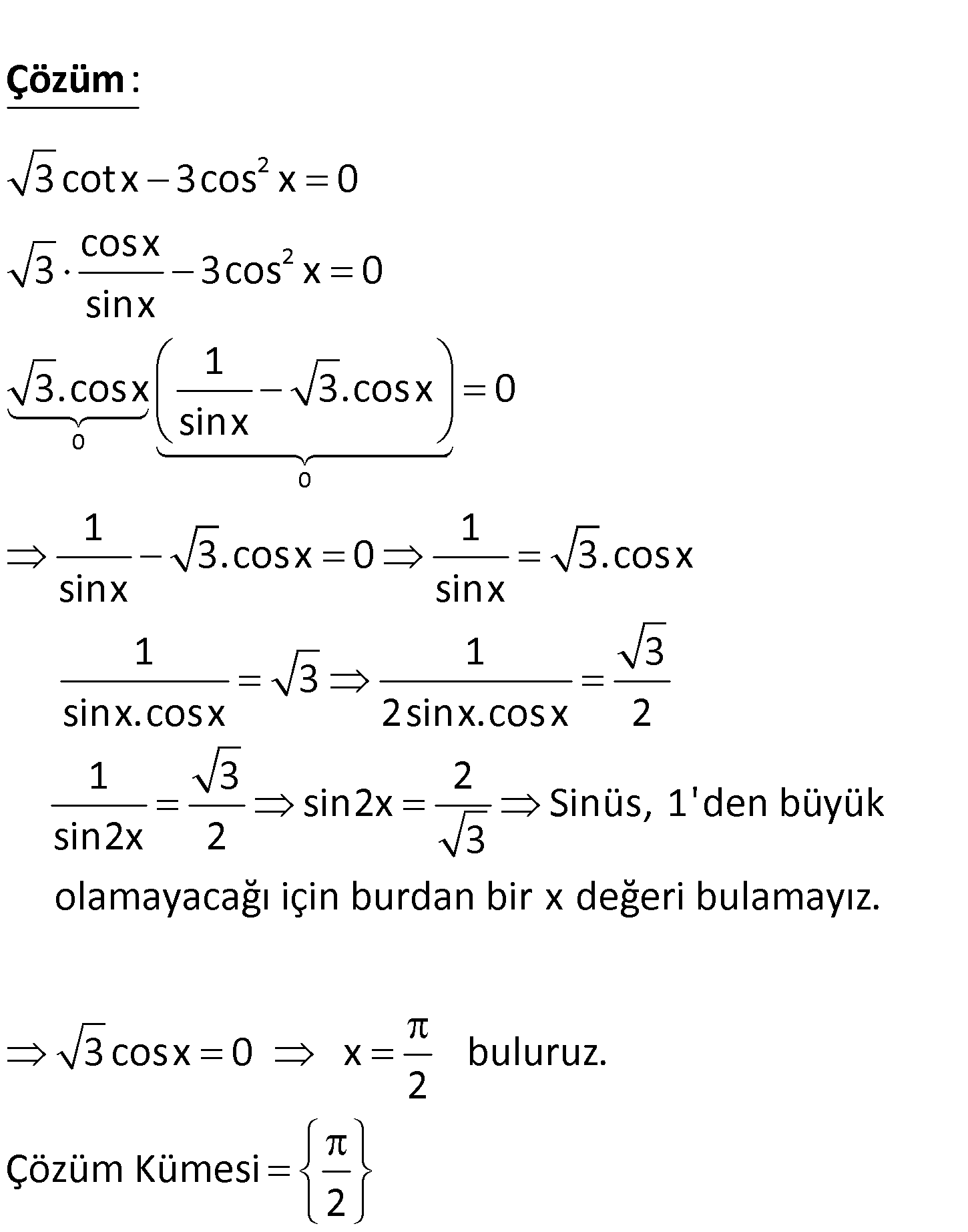
4.SORU


5.SORU
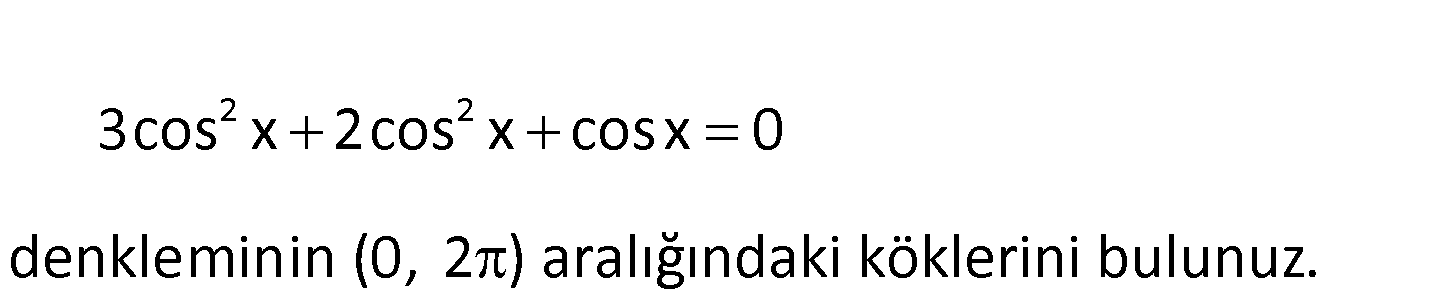

6.SORU
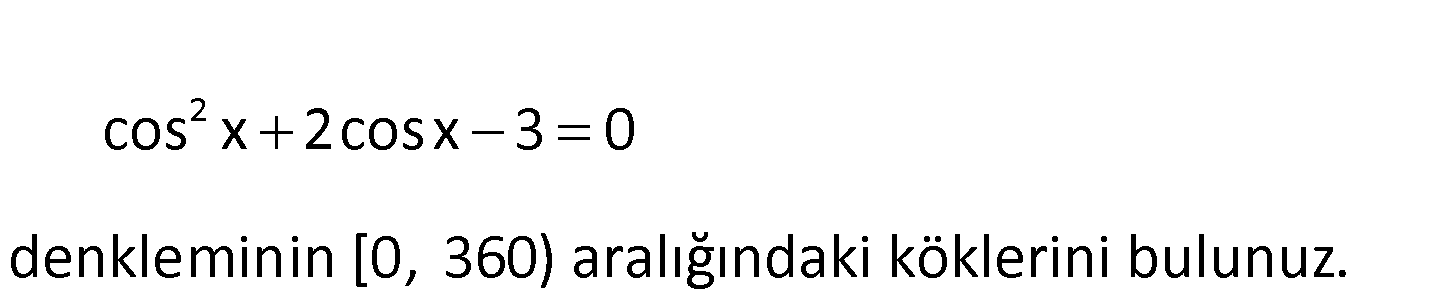

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 6sin x 11cosx 10 denklemini sağlayan x açısı aşağıdakilerden hangisi olabilir? A) B) C) 8 6 4 D) E) 3 2 2 2 2 2 6sin x 11cosx 10 sin x yerine 1 cos x yazabiliriz. 6 1 cos x 11cosx 10 cosx a olsu : n. 6 6a Çözüm 2 2 3a 4 2a 1 11a 10 0 6a 11a 4 0 3a 4 2a 1 4 1 a veya a dir. 3 2 cosx 1’den büyük olamayacağı için 1 cosx dir. 2 x olursa bu eşitlik sağlanır. 3 Cevap: D www.matematikkolay.net 49
2 4cos x 12 3cosx 15 0 denkleminin çözüm kümesini [0, 2 ) aralığında bulunuz. www.matematikkolay.net 2 2cosx 5 3 2cosx 3 4cos x 12 3 cosx 15 0 (2cosx 5 3)(2cosx 3) 0 2cosx 5 3 0 veya 2cosx 3 0 dır. : Çözüm 5 3 2cosx 5 3 0 cosx= cosx 1’den 2 büyük olamayacağı için kök yoktur. 3 11 2cosx 3 0 cosx= x= veya 2 6 6 11 Çözüm Kümesi= , 6 6 4
2 3cotx 3cos x 0 denkleminin çözüm kümesini [0, ) aralığında bulunuz. www.matematikkolay.net 2 2 0 0 3 cotx 3cos x 0 cosx 3 3cos x 0 sinx 1 3.c : osx 3.cosx 0 sinx 1 1 3.cosx 0 sinx Çözüm 3.cosx sinx 1 1 3 3 sinx.cosx 2sinx.cosx 2 1 3 2 sin2x Sinüs, 1’den büyük sin2x 2 3 olamayacağı için burdan bir x değeri bulamayız. 3 cosx 0 x buluruz. 2 Çözüm Kümesi 2 5
www.matematikkolay.net 4sinx.cosx 3 denkleminin çözüm kümesini bulunuz. sin2x 4sinx.cosx 3 2.2sinx.cosx 3 2.sin2x 3 sin2x 1,5 sinüs değeri 1’den büyük ola : maz. Ç Çözüm özüm Kümesi 6
2 2 3cos x 2cos x cosx 0 denkleminin (0, 2 ) aralığındaki köklerini bulunuz. 3 2 2 2 3cos x 2cos x cosx 0 cosx(3cos x 2cosx 1) 0 3 cosx 0 x veya dir. 2 2 3cos x 2cosx 1 0 : Çözüm 2 2 2 denklemine 3x 2x 1 dersek. Bu denklemin diskriminantı b 4ac 2 4.1.3 4 12 8 0’dan küçüktür. Çözüm yoktur. 3 Buna göre; Çözüm Kümesi , 2 2 www.matematikkolay.net 7
2 cos x 2cosx 3 0 denkleminin [0, 360) aralığındaki köklerini bulunuz. 2 (3).( 1) cos x 2cosx 3 0 (cosx 3)(cosx 1) 0 cosx, 1 ile 1 arasında bir değer alabilidğinde : n cos Çözüm x 3 olamaz. Bu nedenle; cosx 1 x 0 dır. Ç.K {0} 8

