Soru Sor sayfası kullanılarak Trigonometri-2 konusu altında Yarım Açı (İki kat açı) Formülleri Güzel Sorular ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…

1.SORU


2.SORU
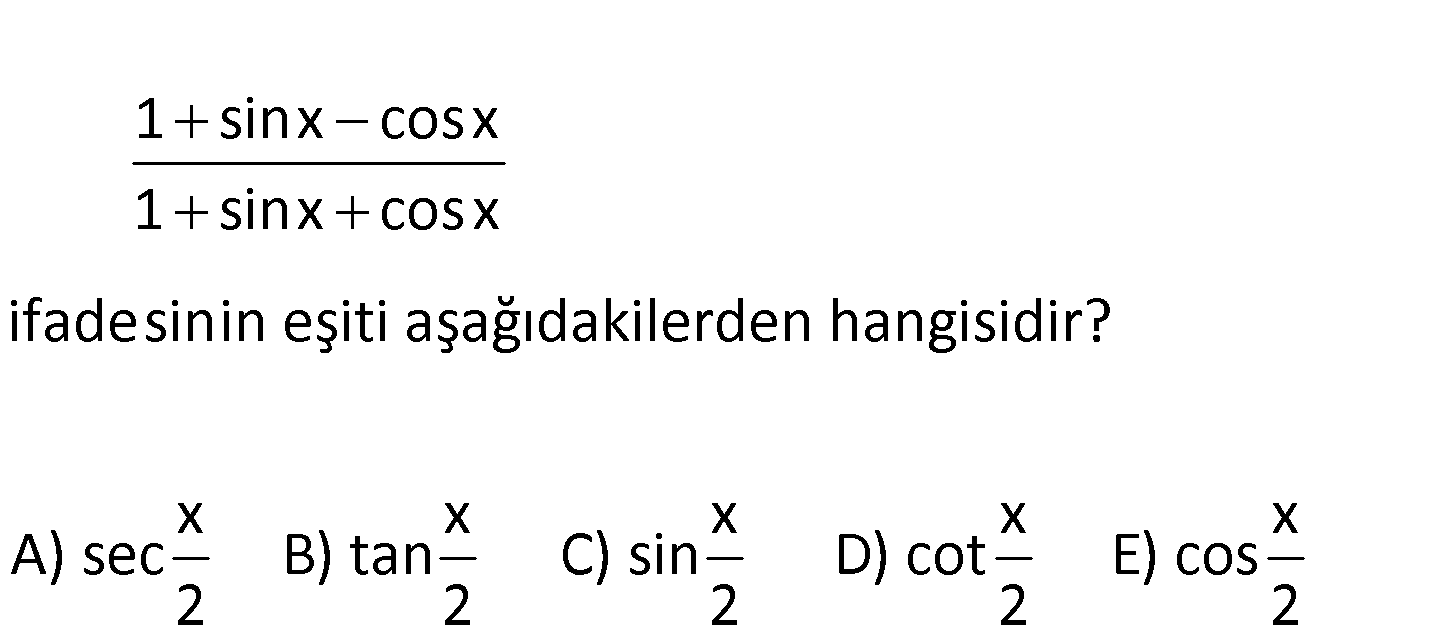
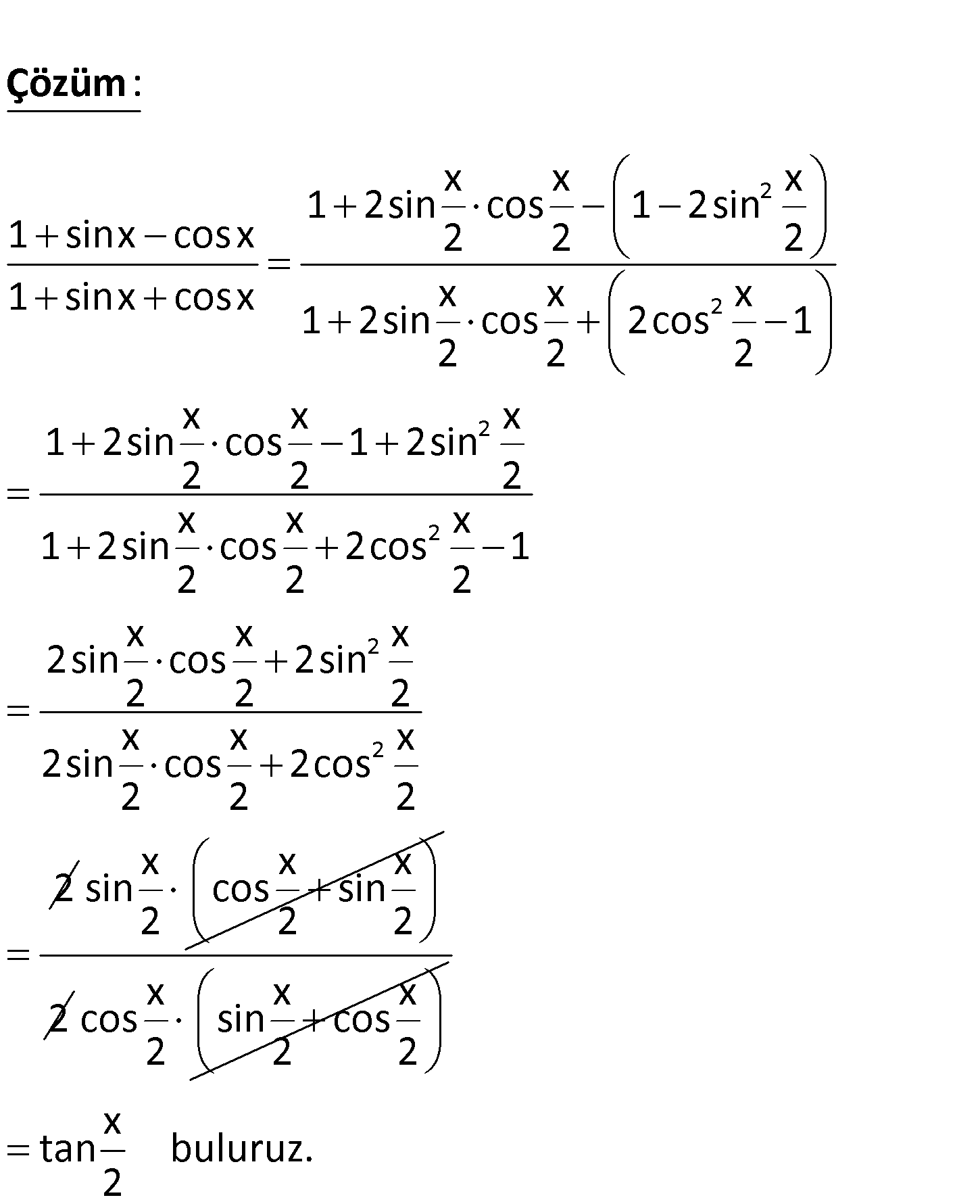
3.SORU
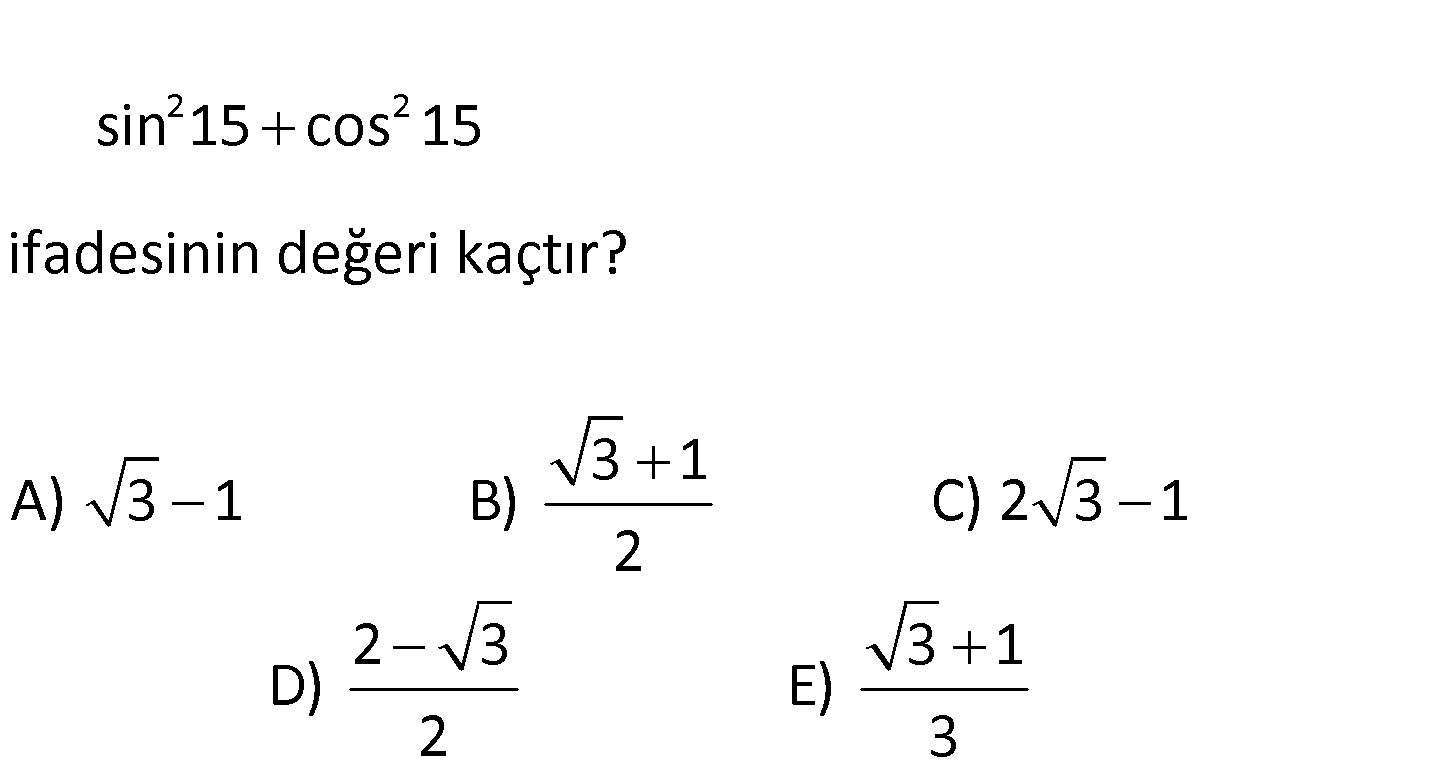
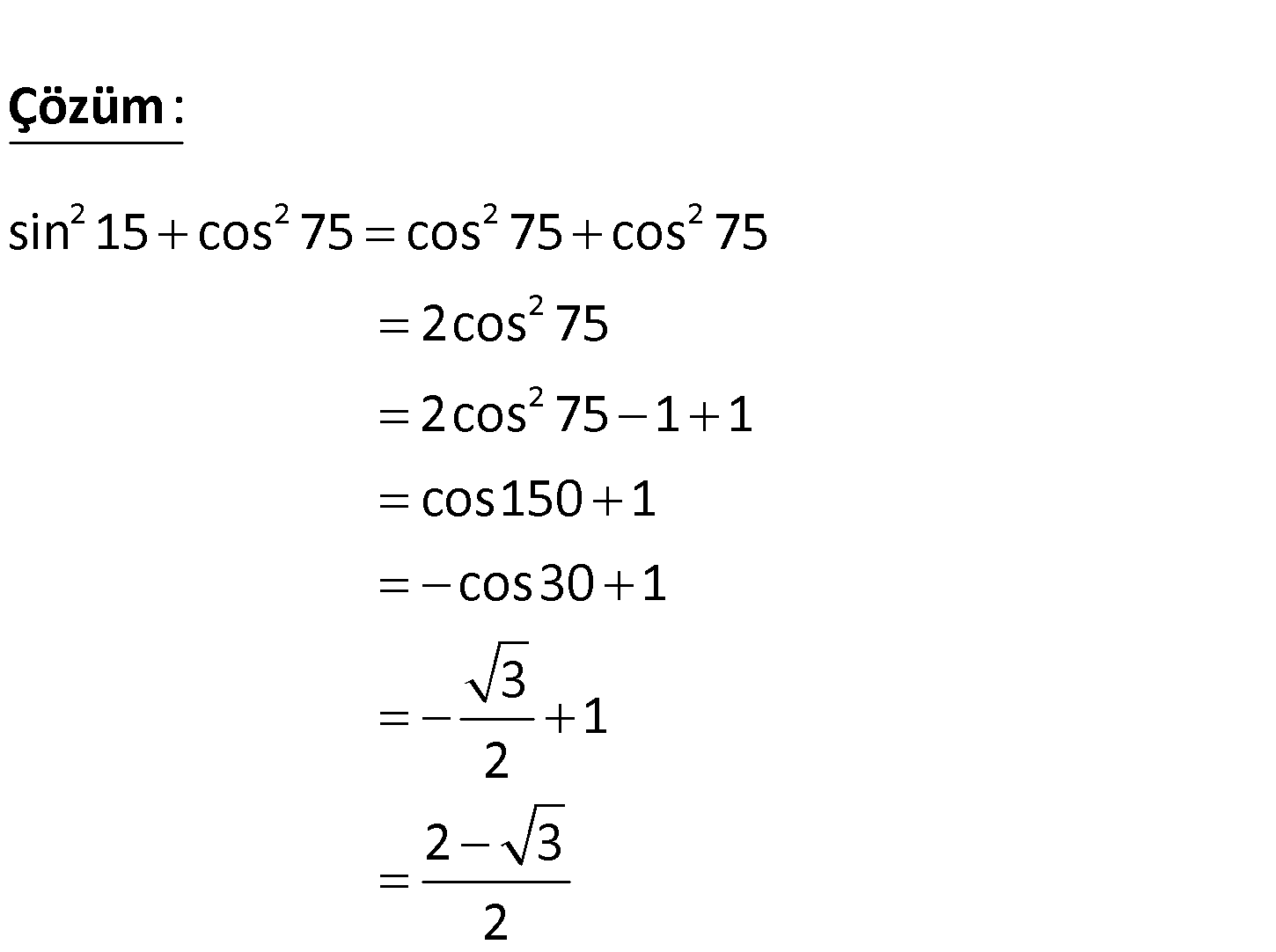
4.SORU
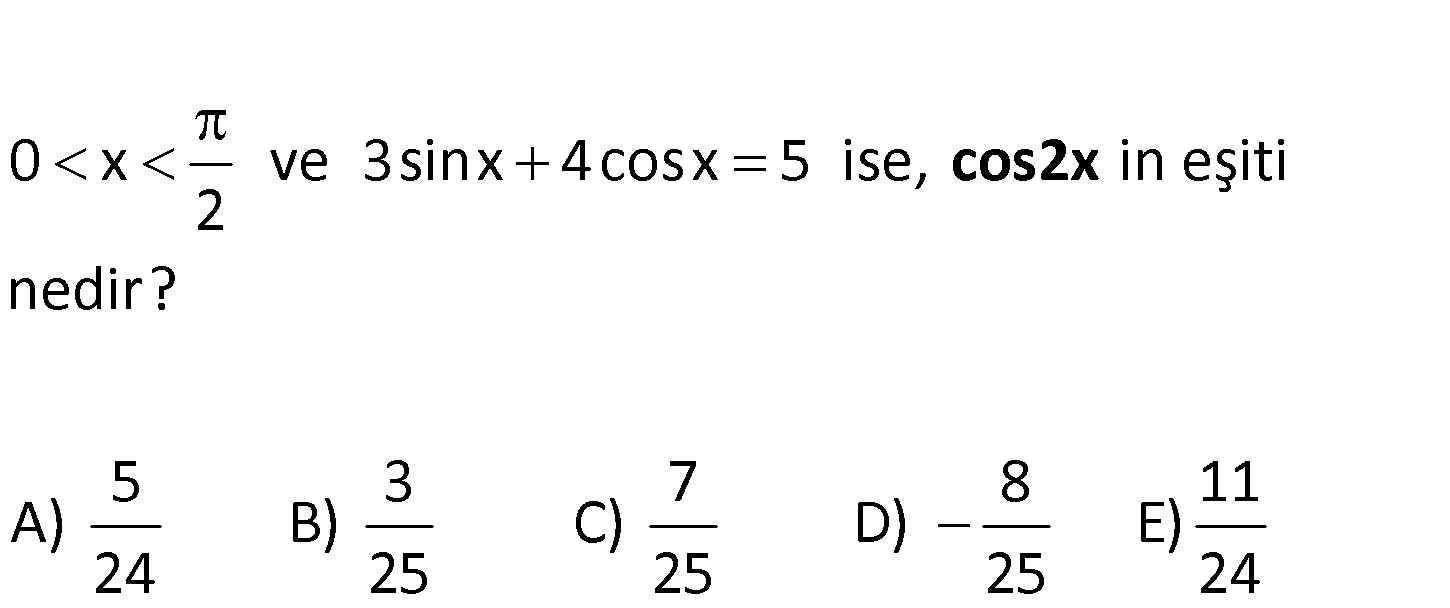

5.SORU


6.SORU
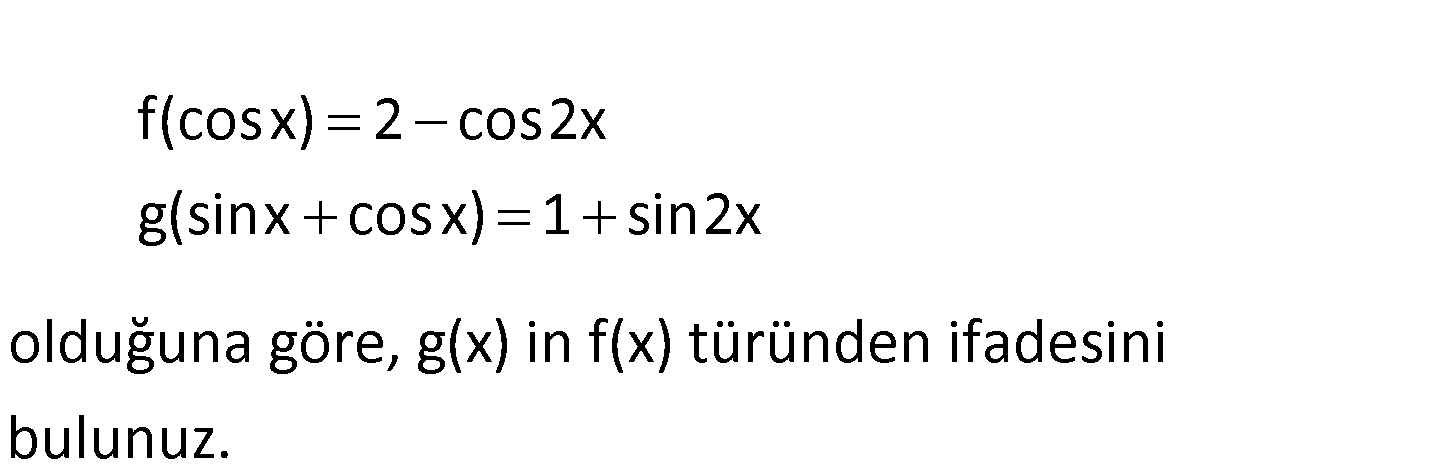

7.SORU
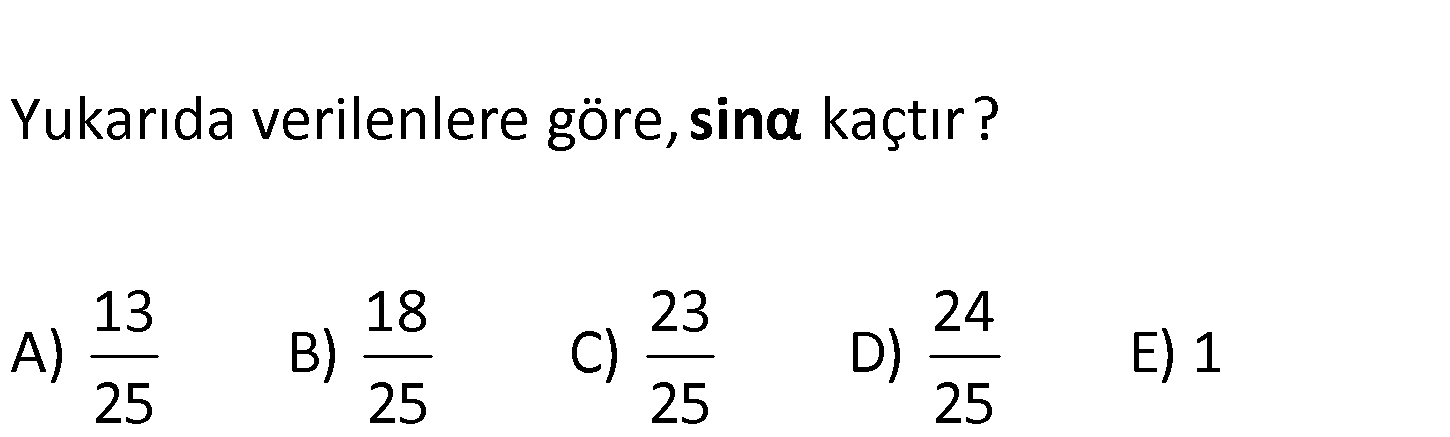

8.SORU
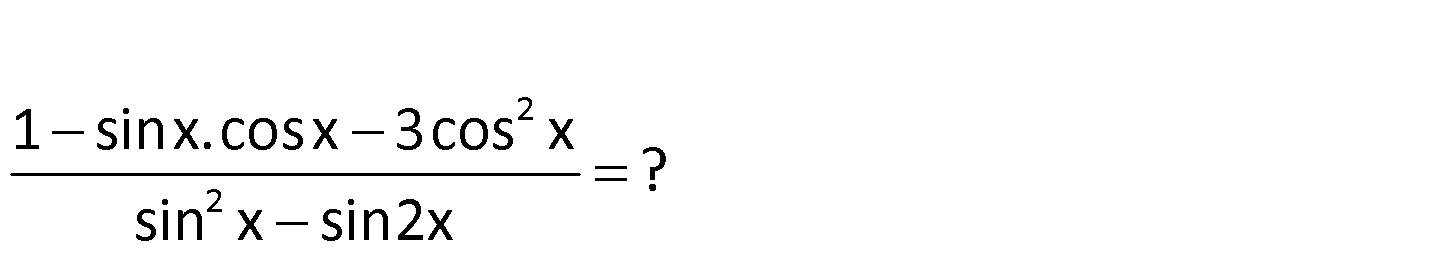

9.SORU
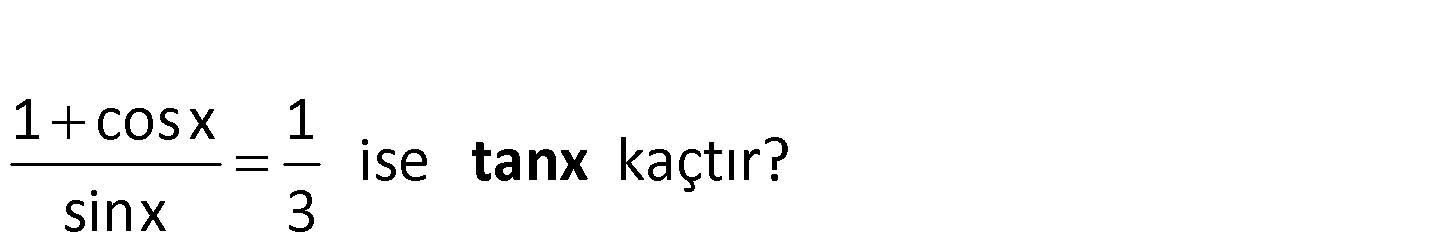
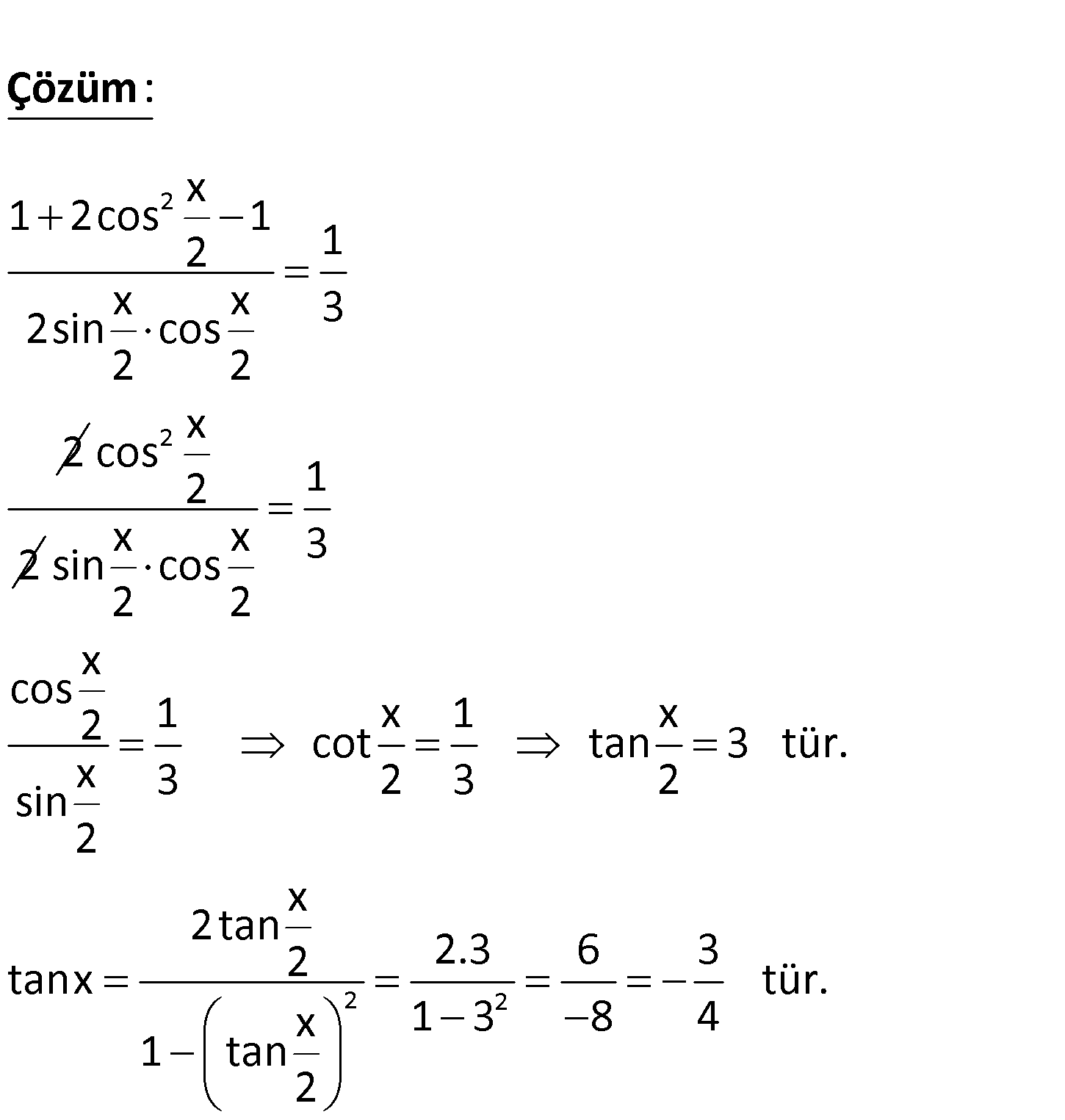
10.SORU
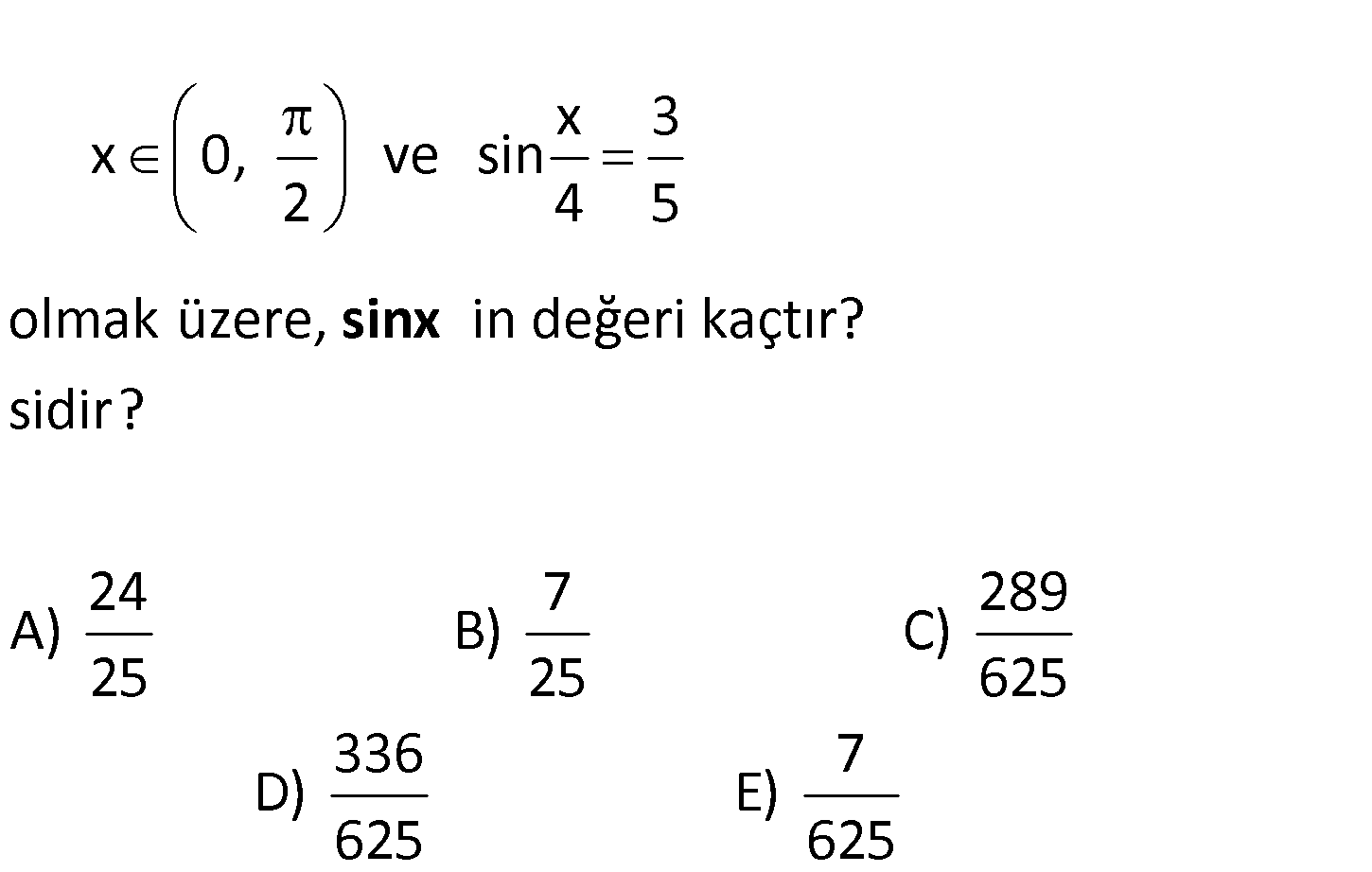

11.SORU


12.SORU

13.SORU
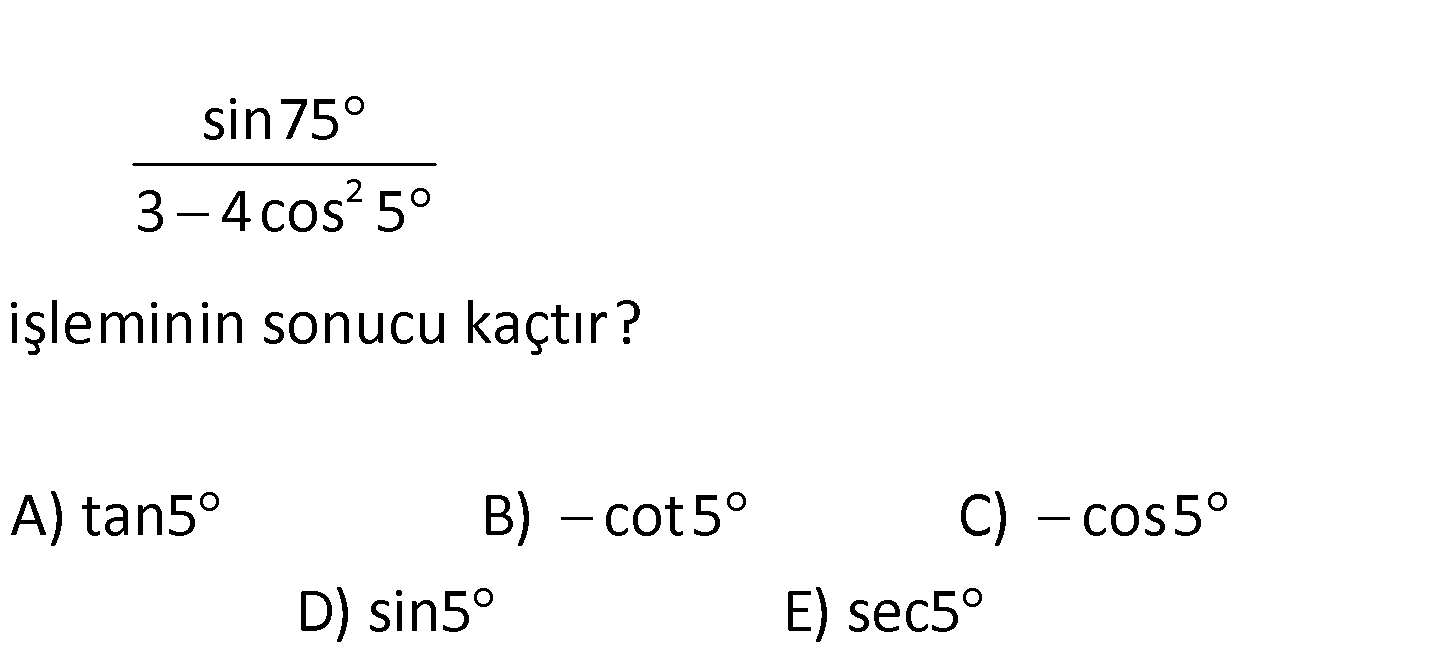

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3 3sinx 4sin x ifadesinin en sade halini bulunuz. 3 3 3 sinx 2sinx 2sin x 2sin x 3 3sinx 4sin x sinx 2sinx 2sin x 2 : Çözüm 3 3 3 2 2 2 sin2x sin x sinx 2sin x 2sinx 2sin x sinx(1 2sin x) 2sinx(1 sin x) sinx.cos2x 2sinxcos x sinx.cos2x 2sinxcosx.cosx sinx.cos2x sin2x.cos2x sin(x 2x) sin3x bulunur. 2
1 sinx cosx 1 sinx cosx ifadesinin eşiti aşağıdakilerden hangisidir? x x x A) sec B) tan C) sin 2 2 2 x x D) cot E) cos 2 2 2 2 x x x 1 2sin cos 1 2sin 1 sinx cosx 2 2 2 1 sinx cosx x x x 1 2sin cos 2cos 1 2 2 2 x 1 2sin 2 : Çözüm 2 2 2 2 x x cos 1 2sin 2 2 x x x 1 2sin cos 2cos 1 2 2 2 x x x 2sin cos 2sin 2 2 2 x x x 2sin cos 2cos 2 2 2 2 x x x sin cos sin 2 2 2 2 x x x cos sin cos 2 2 2 x tan buluruz. 2 17
2 2 sin 15 cos 15 ifadesinin değeri kaçtır? 3 1 A) 3 1 B) C) 2 3 1 2 2 3 D) 3 1 E) 2 3 2 2 2 2 2 sin 15 cos 75 cos 75 cos 75 2cos 75 : Çözüm 2 2cos 75 1 1 cos150 1 cos30 1 3 1 2 2 3 2 91
0 x ve 3sinx 4cosx 5 ise, in eşiti 2 nedir? 5 3 7 8 11 A) B) C) D) E) 24 25 25 25 24 cos2x 2 2 2 2 2 2 2 3sinx 4cosx 5 3 (1 cos x) 5 4cosx 3 (1 cos x) 5 4cosx 9(1 cos x) 25 40co : sx 16cos x 9 9cos x 16co Çözüm 2 2 2 2 s x 40cosx 25 0 25cos x 40cosx 16 0 5cosx 4 4 cosx 5 16 cos2x 2cos x 1 2 1 25 32 7 1 bulunur. 25 25 65
cos36.sin18 ? sin72 cos36.sin18 x olsun. İki tarafı da 2sin36 ile çarpalım. 2sin36.cos36.sin18 x. : Çözüm cos18 2sin36 sin72.sin18 x.2sin36 cos18.sin18 x.2sin36 1 sin36 2 x.2 sin36 1 1 2x x buluruz. 2 4 62
f(cosx) 2 cos2x g(sinx cosx) 1 sin2x olduğuna göre, g(x) in f(x) türünden ifadesin i bulunuz. 2 2 2 f(cosx) 2 cos2x 2 (2cos x 1) 3 2cos x tir. f(a) 3 a şeklin : d Çözüm 2 2 2 2 2 e bir fonksiyondur. sinx cosx ifadesinin karesine bakalım. (sinx cosx) sin x cos x 2sinx.cosx 1 sin2x tir. Buna göre; g(sinx cosx) 1 sin2x g(a) a dir. f(x) 3 x idi. f(x) 3 g(x) g(x) 3 f(x) buluruz. 42
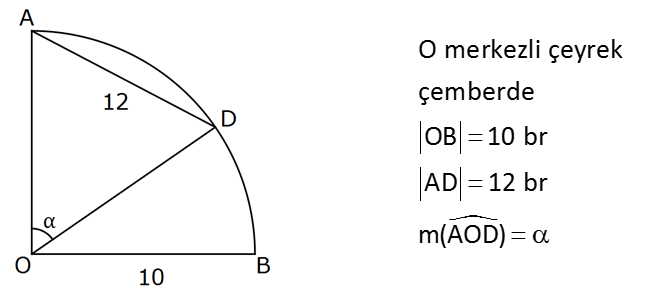
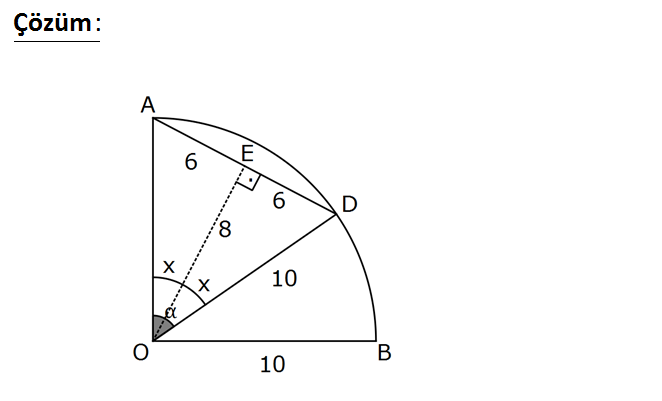
O merkezli çeyrek çemberde OB 10 br AD 12 br m(AOD) Yukarıda verilenlere göre, kaçtır? 13 18 23 24 A) B) C) D) E) 1 25 25 25 25 sinα : Çözüm Çeyrek çemberde OA ve OD uzunlukları yarı çap olduğundan 10 cm dir.İkizkenar üçgenden diklik inersek iki eş 6 – 8 – 10 üçgeni bulunur. açısı iki eş parçaya bölünür.Bu açılara x diyelimBuradan sin yarım açı formülünden; 6 sin sin2x 2sinx.cosx 2. 3 10 5 8 4 10 5 24 buluruz. 25 46
2 2 1 sinx.cosx 3cos x ? sin x sin2x 2 2 2 2 2 2 2 1 sinx.cosx 3cos x sin x sin2x sin x cos x sinx.cosx 3cos x sin x 2sinx.ccosx sin x sinx.cos : x Çözüm 2 2cos x sinx(sinx 2cosx) (sinx 2cosx) .(sinx cosx) sinx (sinx 2cosx) sinx cosx sinx 1 cotx tir. 58
1 cosx 1 ise kaçtır? sinx 3 tanx 2 x 1 2cos 1 2 1 x x 3 2sin cos 2 2 2 : Çözüm 2 x cos 2 2 2 2 1 x x 3 sin cos 2 2 x cos 2 1 x 1 x cot tan 3 tür. x 3 2 3 2 sin 2 x 2tan 2 2.3 6 3 tanx tür. x 1 3 8 4 1 tan 2 76
x 3 x 0, ve sin 2 4 5 olmak üzere, in değeri kaçtır? sidir? 24 7 289 A) B) C) 25 25 62 sinx 5 336 7 D) E) 625 625 x 3 x 4 Dik üçgen çizilerek sin ise cos tir. 4 5 4 5 bulunabilir. 3- 4 – 5 x x sin 2 sin cos 2 4 : Çözüm x 3 4 24 2 olur. 4 5 5 25 x 24 x 7 sin ise cos tir. 7 24 25 Üçgeni 2 25 2 25 x x 24 7 336 sinx 2 sin cos 2 buluruz. 2 2 25 25 625 93
tan(a b) 4 tan(a b) 2 olduğuna göre, nın değeri kaçtır? tan2a (a b) (a b) 2a dır. Tan jant toplam formülünü kullanarak tan2a ‘yı bulabiliriz. tan(2a) : Çözüm tan((a b) (a b)) tan(a b) tan(a b) 1 tan(a b). tan(a b) 4 2 6 6 6 buluruz. 1 4.2 1 8 7 7 98
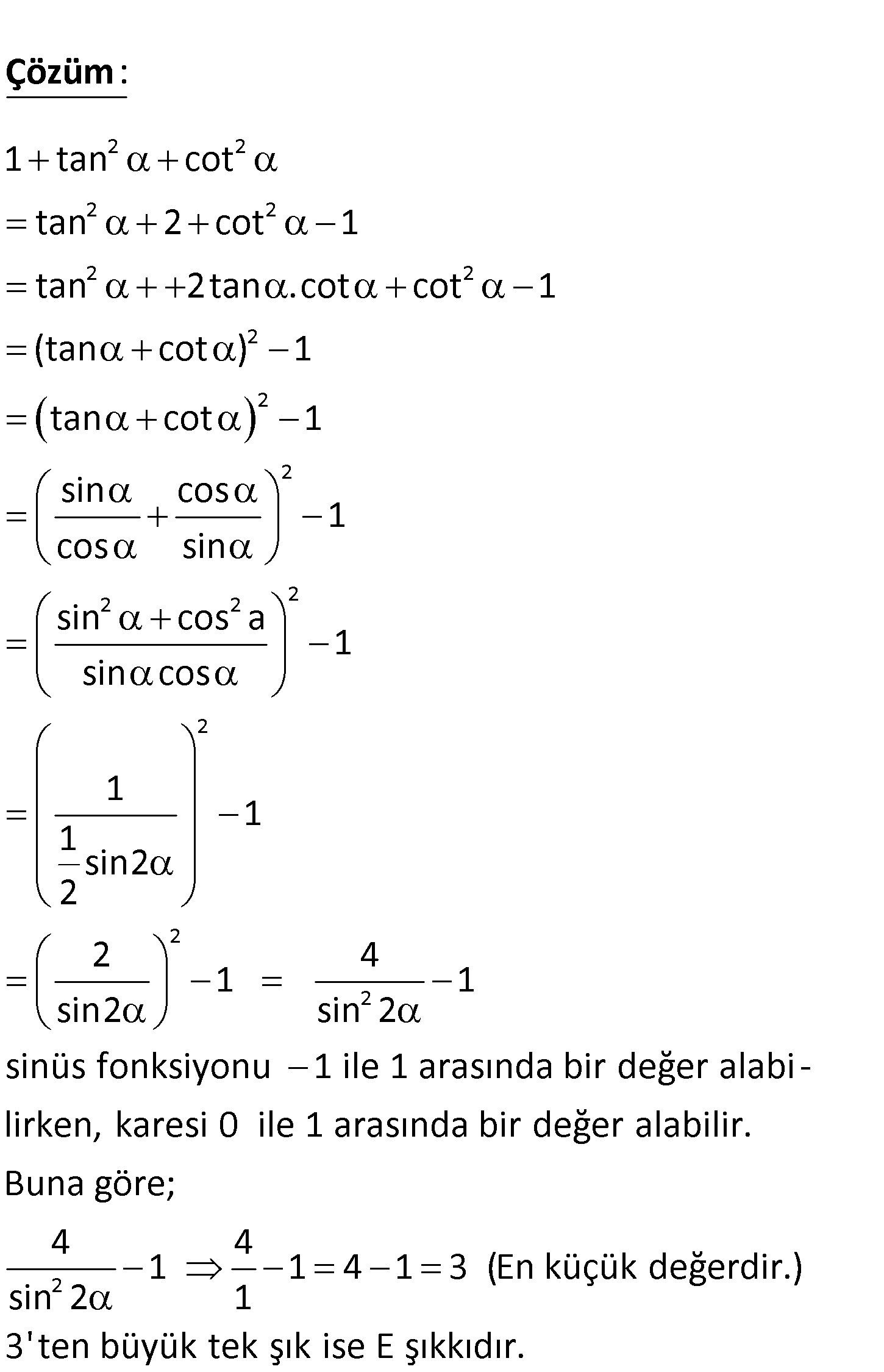
2 2 1 tan cot toplamı aşağıdakilerden hangisine eşit olabilir? 1 3 5 11 A) B) C) 2 D) E) 2 2 2 3 2 2 2 2 2 2 2 2 1 tan cot tan 2 cot 1 tan 2tan .cot cot 1 (tan cot ) 1 tan cot 1 sin cos : Çözüm 2 2 2 2 2 2 2 cos 1 sin sin cos a 1 sin cos 1 1 1 sin2 2 2 4 1 1 sin2 sin 2 sinüs fonksiyonu 1 ile 1 arasında bir değer alabi – lirken, karesi 0 ile 1 arasında bir değer alabili 2 r. Buna göre; 4 4 1 1 4 1 3 (En küçük değerdir.) sin 2 1 3’ ten büyük tek şık ise E şıkkıdır. 99
2 sin75 3 4cos 5 işleminin sonucu kaçtır? A) tan5 B) cot5 C) cos5 D) sin5 E) sec5 2 2 2 2 sin75 cos15 cos10.cos5 sin10.sin5 3 4cos 5 3 4cos 5 3 2.(2cos 5) (2cos 5 1).cos5 (2sin5.cos5).s : Çözüm 2 3 2 5 2 5 2 in5 3 2.(2cos 5) 2cos 5 cos5 2sin 5.cos5 3 2(cos10 1) cos5(2cos 5 1 2sin 5) 3 2cos10 2 cos5(2cos 5 2sin 5 1) cos5 (2cos10 1) 1 2cos10 1 1 2cos10 cos5 buluruz. 7

