Soru Sor sayfası kullanılarak Trigonometri-2 konusu altında Sinüs yarım açı formülü, sin2a, Sinüs iki kat açı formülleri ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
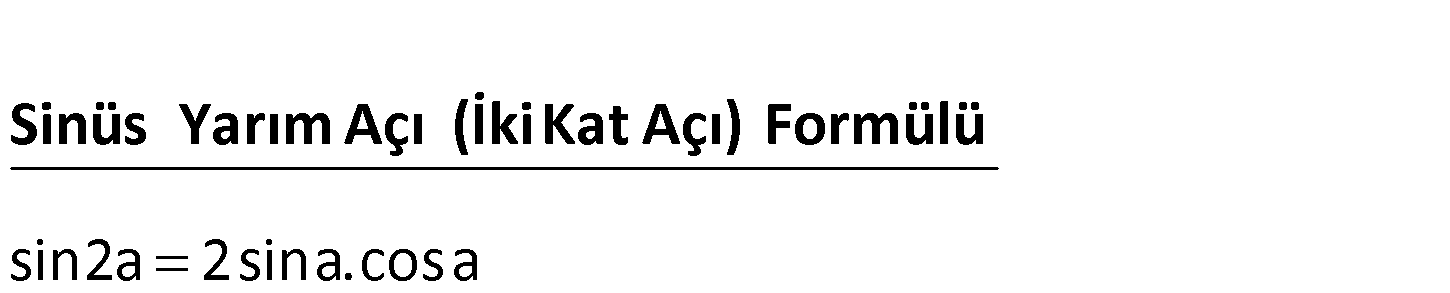
1.SORU
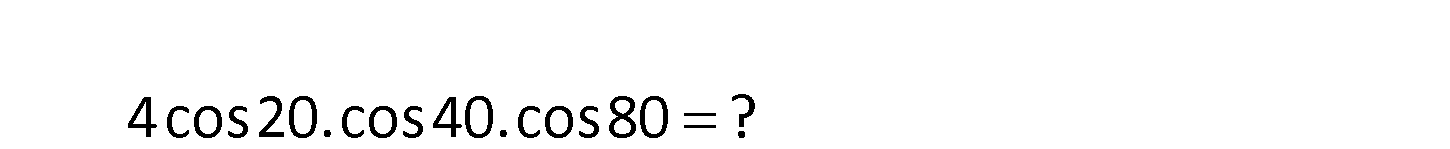
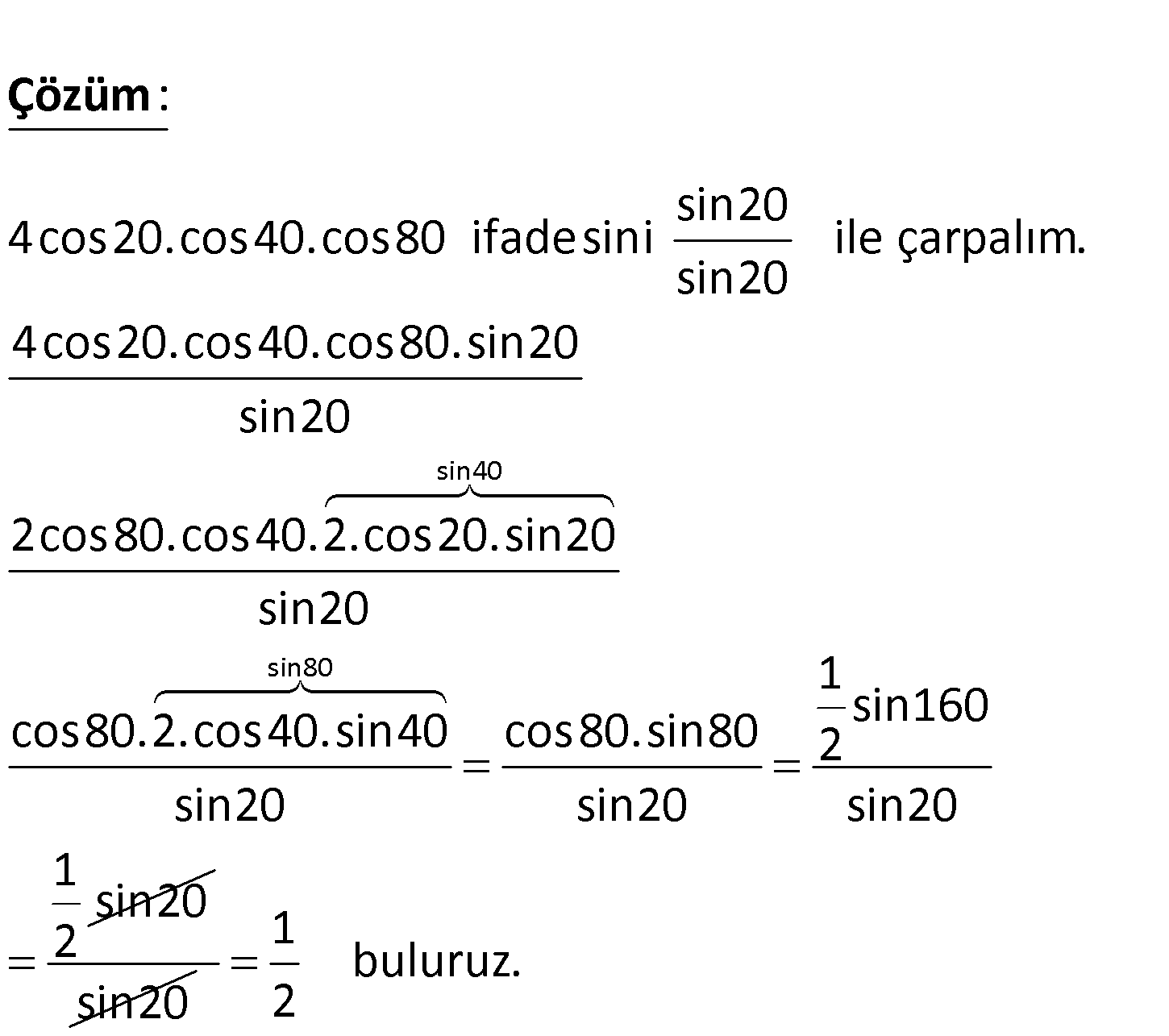
2.SORU
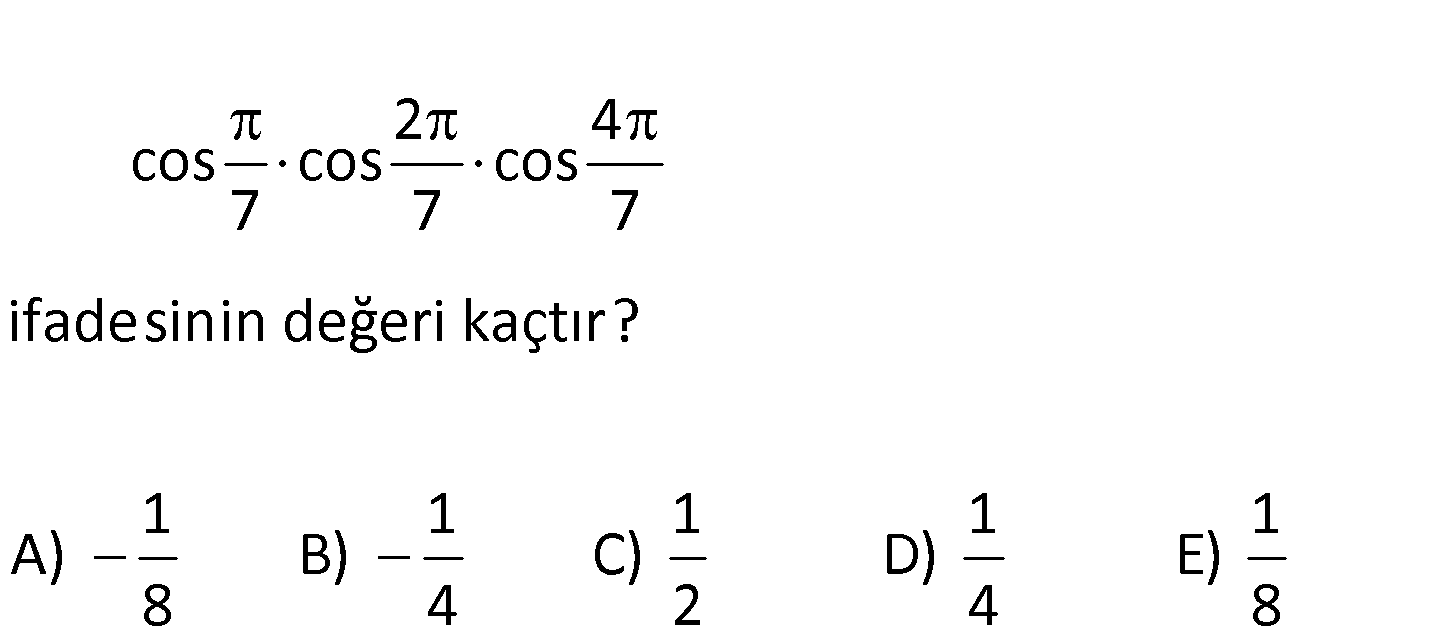
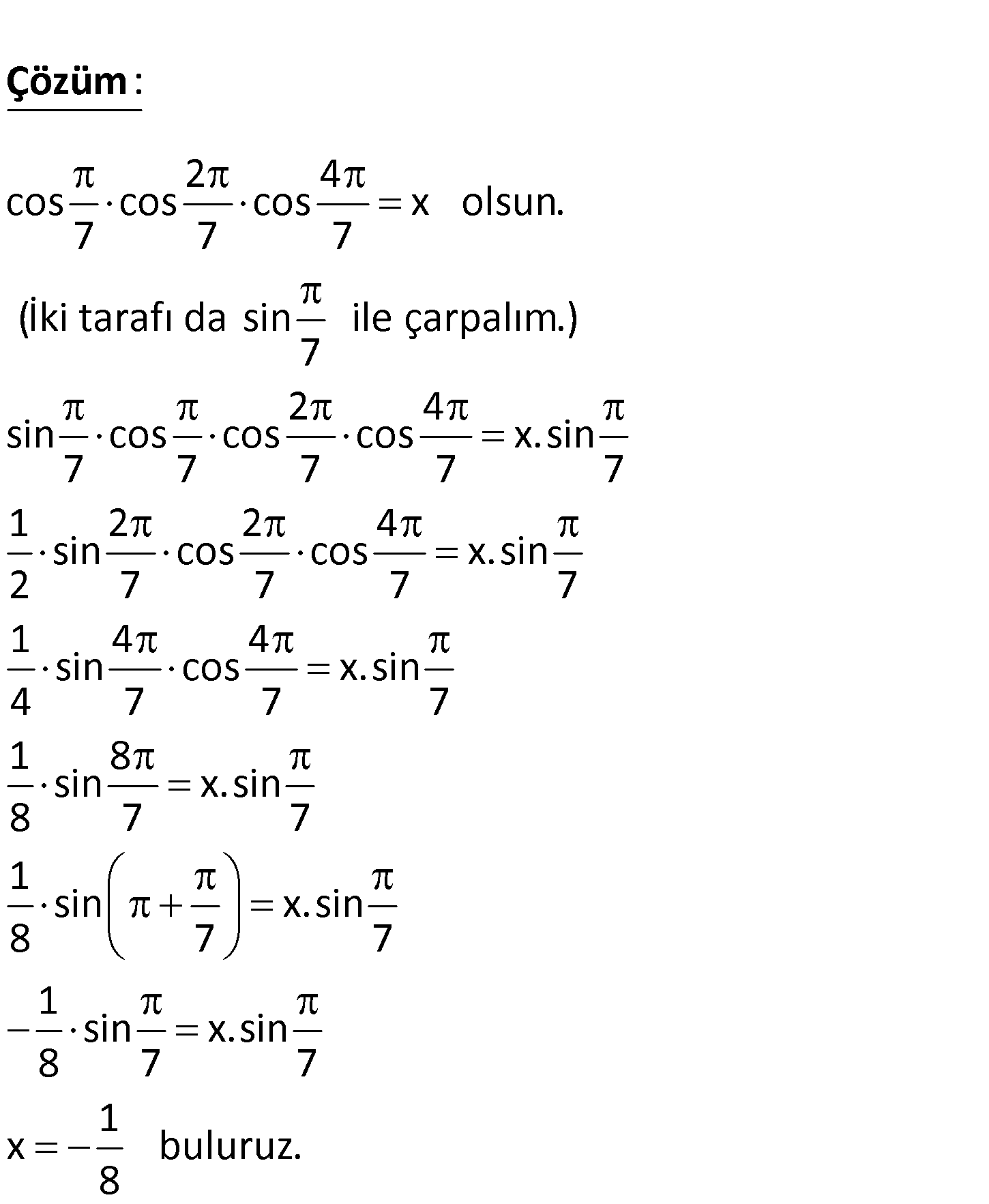
3.SORU
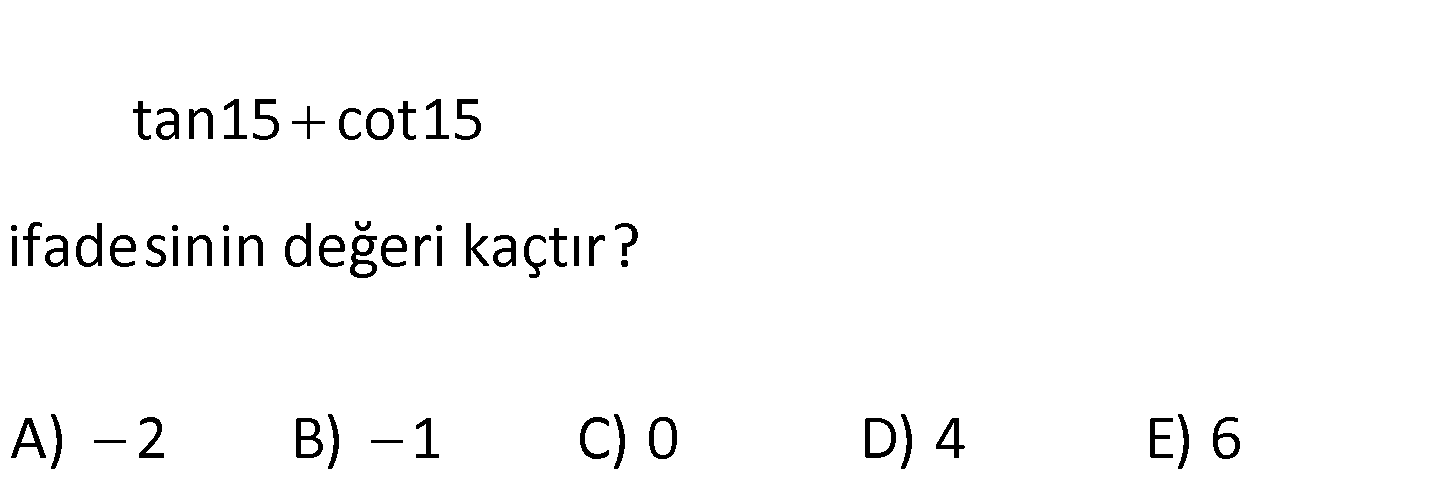
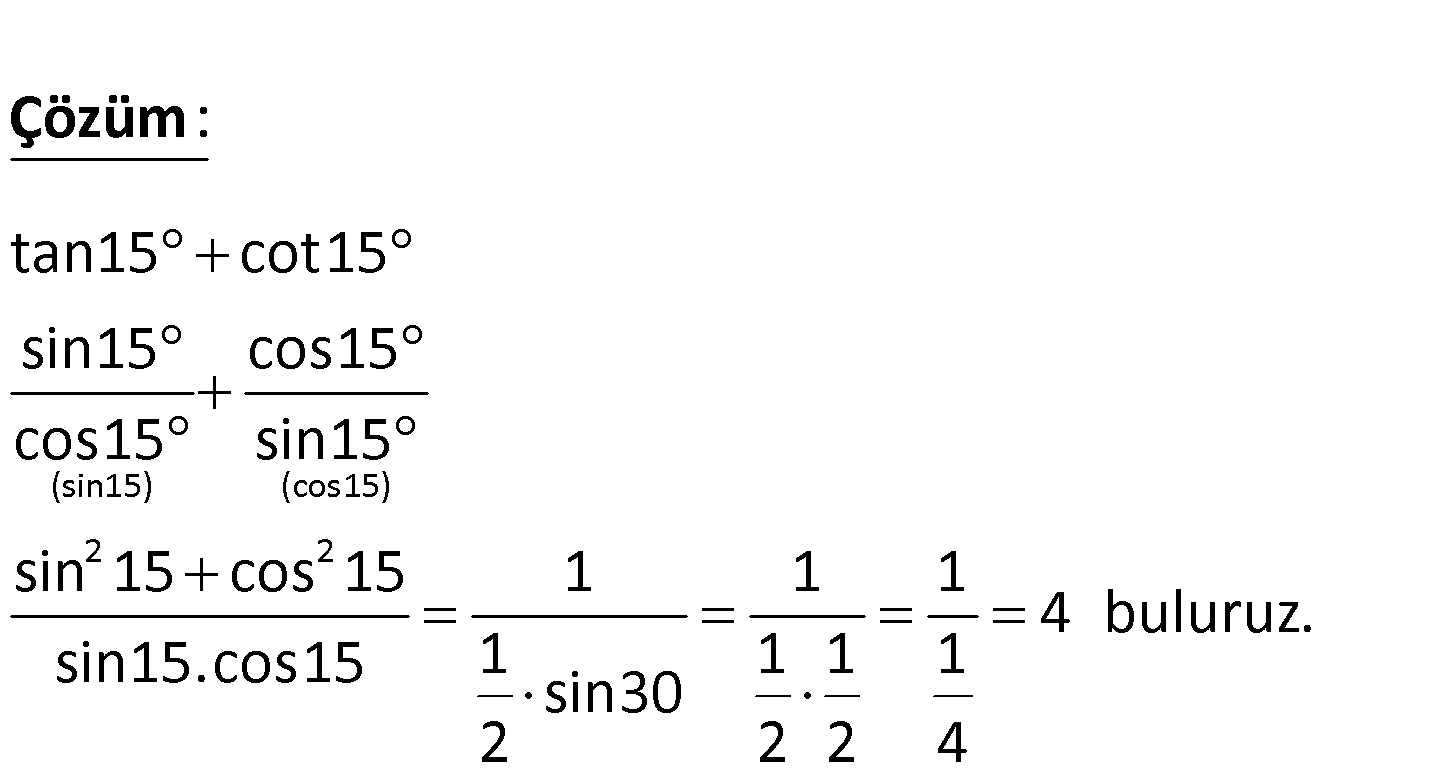
4.SORU

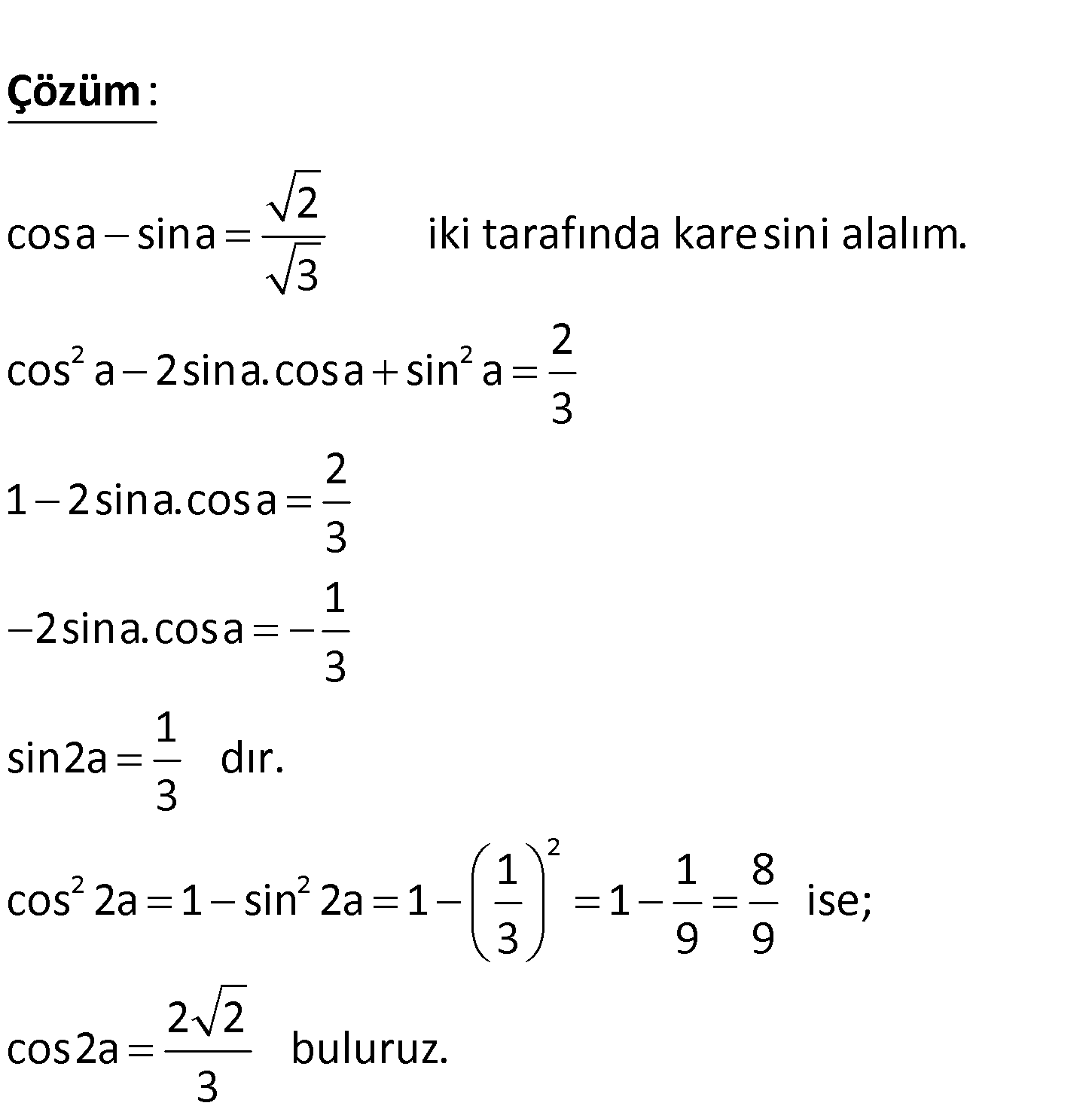
5.SORU
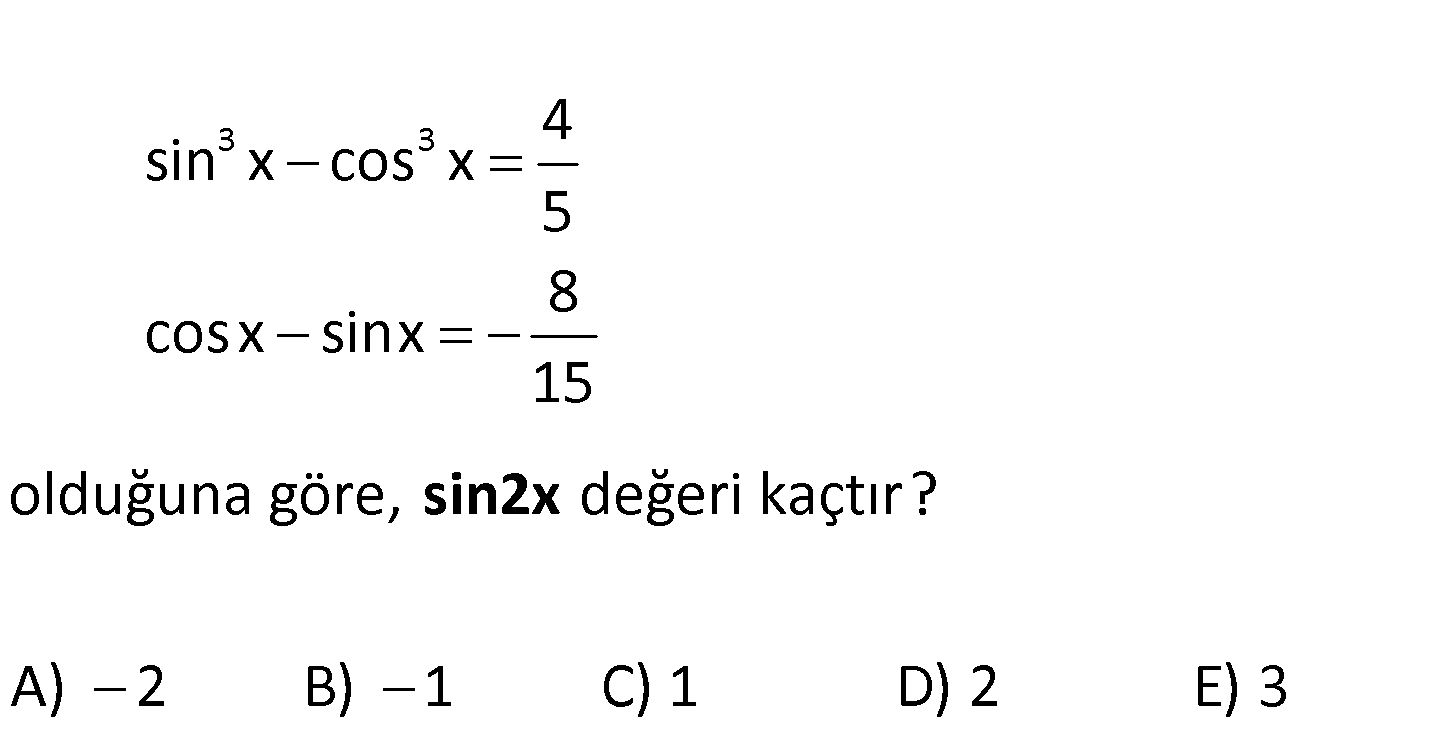
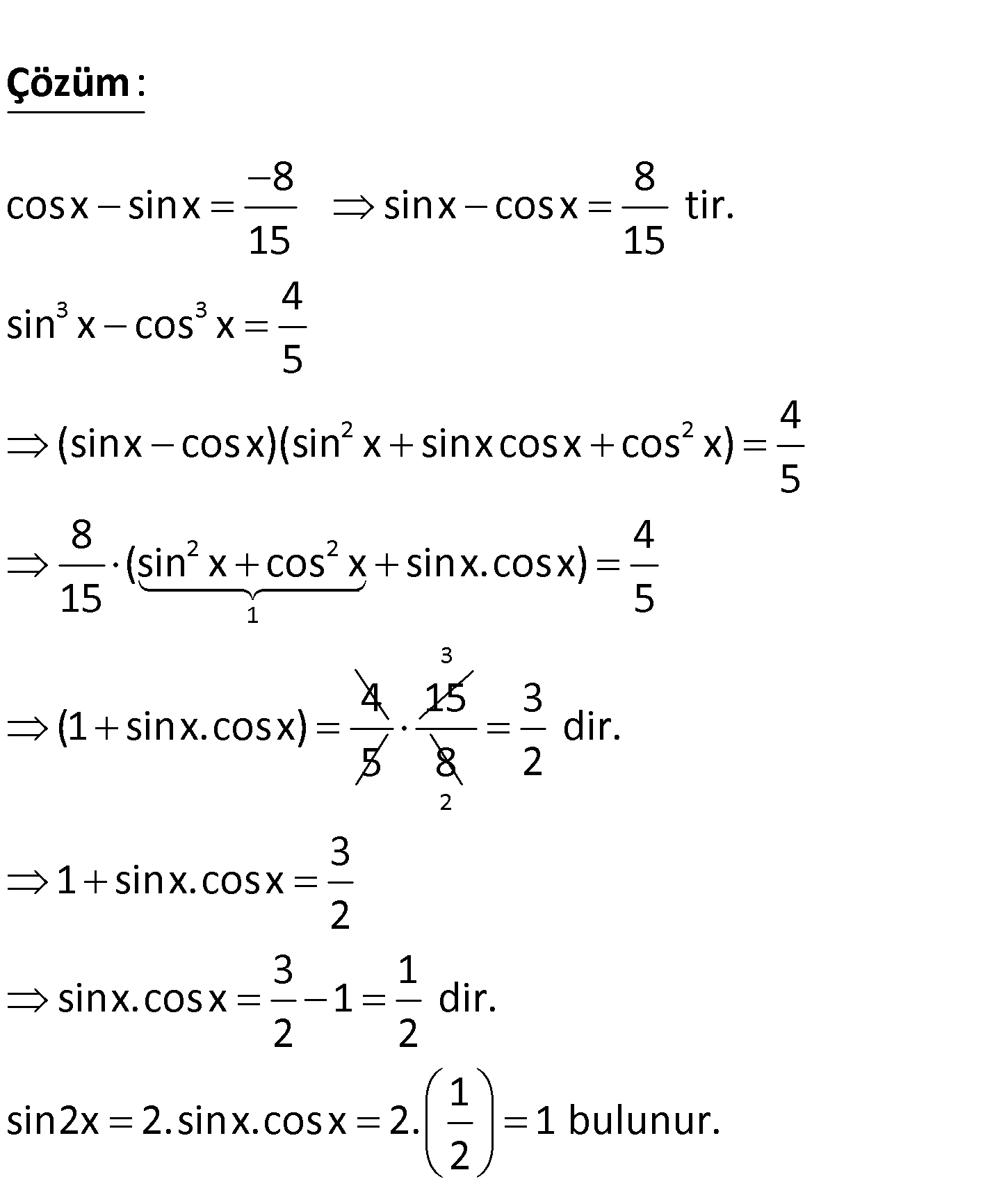
6.SORU
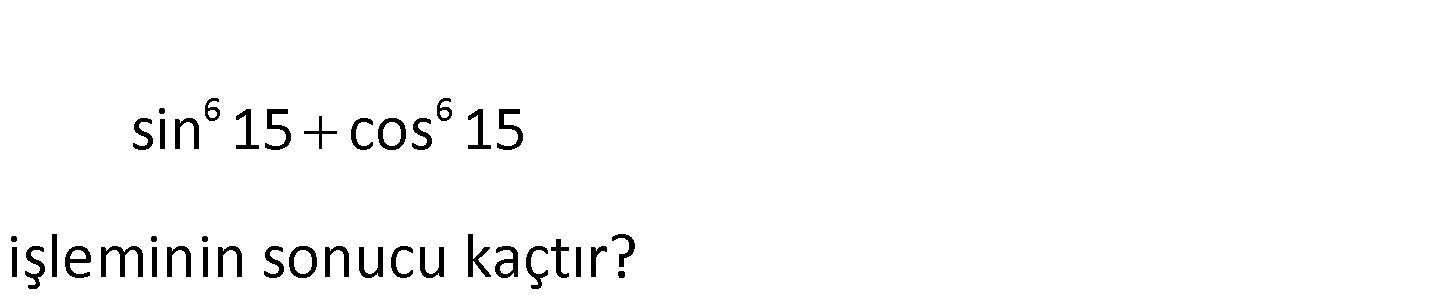
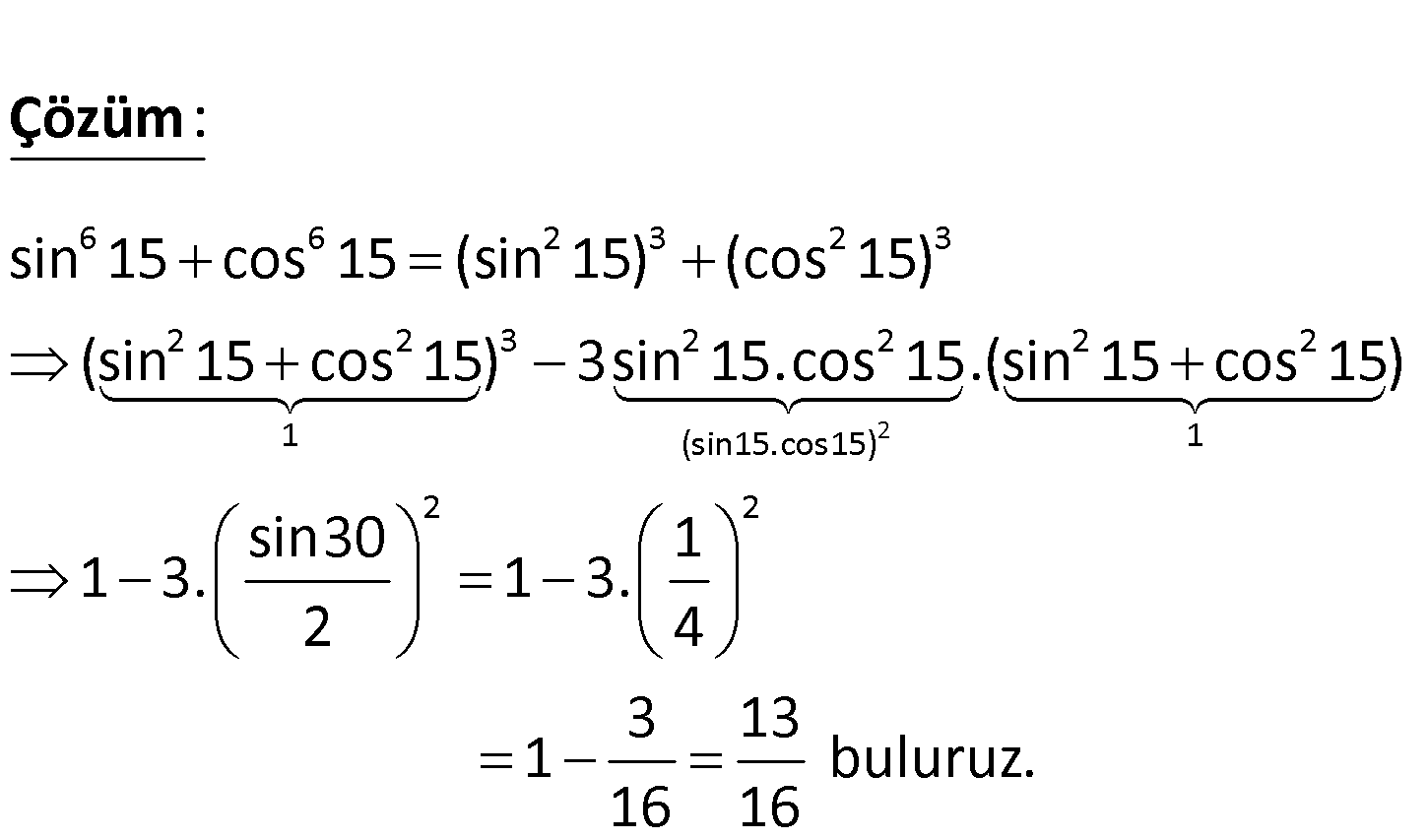
7.SORU


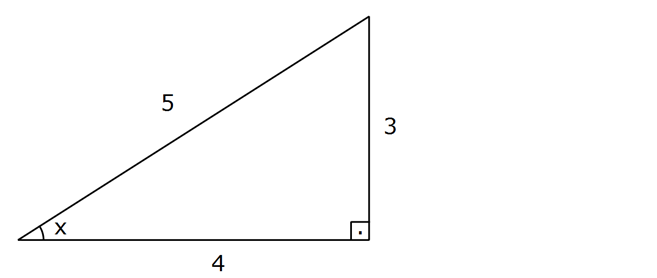

8.SORU


9.SORU
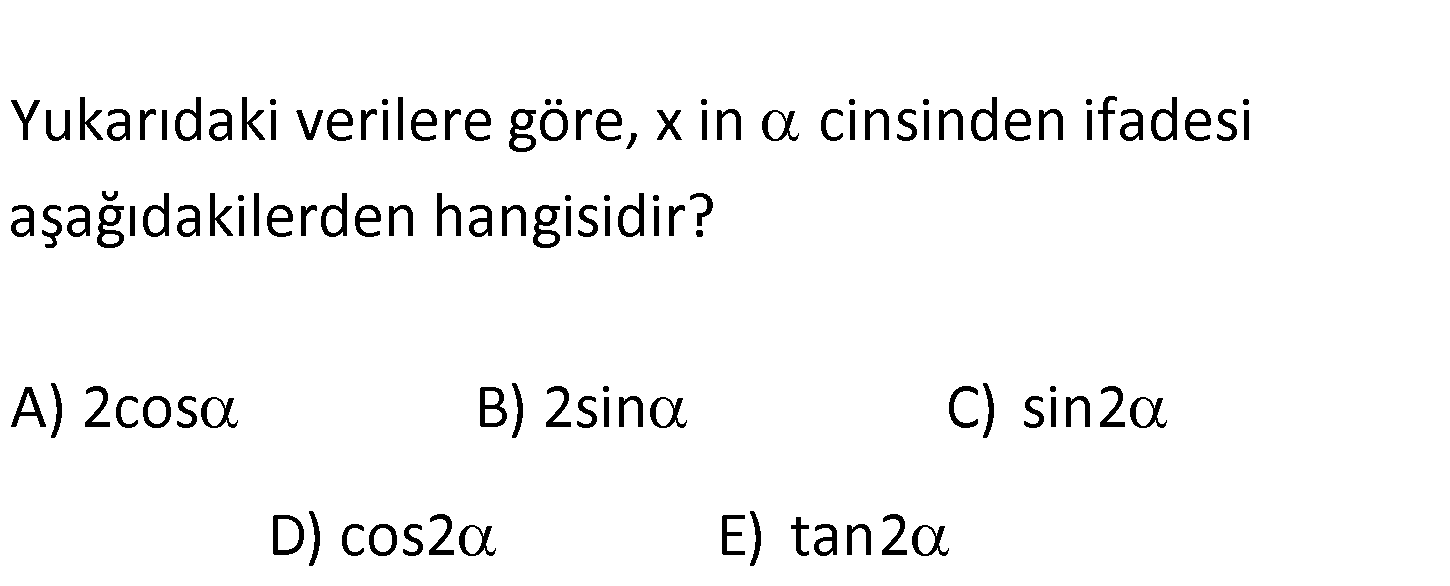

10.SORU
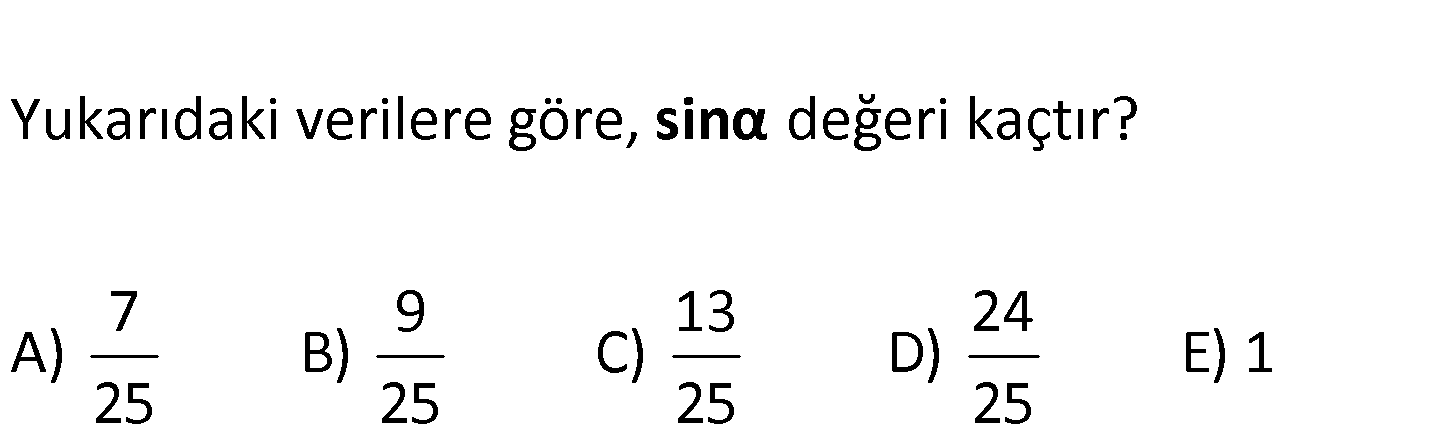

11.SORU

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
4cos20.cos40.cos80 ? sin20 4cos20.cos40.cos80 ifadesini ile çarpalım. sin20 4cos20.cos40.cos80.sin20 sin20 2c : os80. Çözüm sin40 sin80 cos40.2.cos20.sin20 sin20 1 sin160 cos80.2.cos40.sin40 cos80.sin80 2 sin20 sin20 sin20 1 sin20 2 sin20 1 buluruz. 2 13
2 4 cos cos cos 7 7 7 ifadesinin değeri kaçtır? 1 1 1 1 1 A) B) C) D) E) 8 4 2 4 8 2 4 cos cos cos x olsun. 7 7 7 (İki tarafı da sin ile çarpalım.) 7 2 sin cos cos co 7 7 : 7 Çözüm 4 s x.sin 7 7 1 2 2 4 sin cos cos x.sin 2 7 7 7 7 1 4 4 sin cos x.sin 4 7 7 7 1 8 sin x.sin 8 7 7 1 sin x.sin 8 7 7 1 sin x.sin 8 7 7 1 x buluruz. 8 14
tan15 cot15 ifadesinin değeri kaçtır? A) 2 B) 1 C) 0 D) 4 E) 6 (sin15) (cos15) 2 2 : tan15 cot15 sin15 cos15 cos15 sin15 sin 15 cos 15 1 1 sin15.cos15 1 1 1 sin30 2 2 Çözüm 1 4 buluruz. 1 2 4 15
a 0, olmak üzere, 4 3 cosa sina 2 olduğuna göre, ifadesinin değeri kaçtır? cos2a 2 2 2 cosa sina iki tarafında karesini alalım. 3 2 cos a 2sina.cosa sin a 3 2 1 2sina.co a 3 : s Çözüm 2 2 2 1 2sina.cosa 3 1 sin2a dır. 3 1 1 8 cos 2a 1 sin 2a 1 1 ise; 3 9 9 2 2 cos2a buluruz. 3 38
3 3 4 sin x cos x 5 8 cosx sinx 15 olduğuna göre, değeri kaçtır? A) 2 B) 1 C) 1 D) sin2x 2 E) 3 3 3 2 2 8 8 cosx sinx sinx cosx tir. 15 15 4 sin x cos x 5 4 (sinx cosx)(sin x sinxcosx cos x) 5 8 15 : Çözüm 2 2 1 4 (sin x cos x sinx.cosx) 5 4 (1 sinx.cosx) 5 15 3 8 2 3 dir. 2 3 1 sinx.cosx 2 3 1 sinx.cosx 1 dir. 2 2 1 sin2x 2.sinx.cosx 2. 1 bulunur. 2 44
6 6 sin 15 cos 15 işleminin sonucu kaçtır? 2 6 6 2 3 2 3 2 2 3 2 2 1 (sin15.cos15) sin 15 cos 15 (sin 15) (cos 15) (sin 15 cos 15) 3sin 15.cos 1 : 5 Çözüm 2 2 1 2 2 .(sin 15 cos 15) sin30 1 1 3. 1 3. 2 4 3 13 1 buluruz. 16 16 47
x 0, olmak üzere, 2 4 cosx 5 olduğuna göre, nedir? sin2x 4 Kosinüsü olan bir x açısı çizelim. 5 Bunu 3- 4 – 5 üçgeni üzerinde gösterebil : iriz. Çözüm Not : sin2x 2sinx.cosx tir. Buna göre; 3 4 24 sin2x 2 buluruz. 5 5 25 74
2 2 2 sin 2arccosx ifadesinin x türünden değeri aşağıdakilerden hangisidir? A) 1x B) x x 1 C) 2x 1x 2 2 D) 2x x 1 E) x x 1 2 2 2 2 2 arccosx a olsun. cosa x olur. sin a cos a 1 formülünü kullanarak sin a x 1 sin a 1 x : Çözüm 2 2 2 2 sina 1 x dir. sin 2arccosx sin2a 2sina.cosa 2 1 x .x 2x 1 x dir. 92
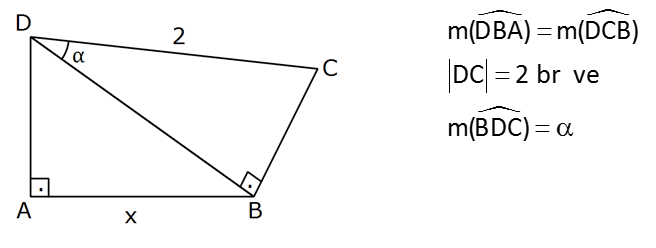
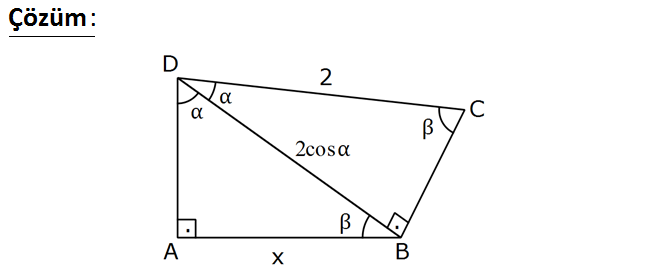
m(DBA) m(DCB) DC 2 br ve m(BDC) Yukarıdaki verilere göre, x in cinsinden ifadesi aşağıdakilerden hangisidir? A) 2cos B) 2sin C) s in2 D) cos2 E) tan2 : Çözüm DCB üçgenine göre; DB DB cos dir. DB 2cos olur. DC 2 DAB üçgenine göre; AB x sin dir. DB DB DB 2cos yazalım. x sin 2cos 2sin cos x sin2 x buluruz. 95
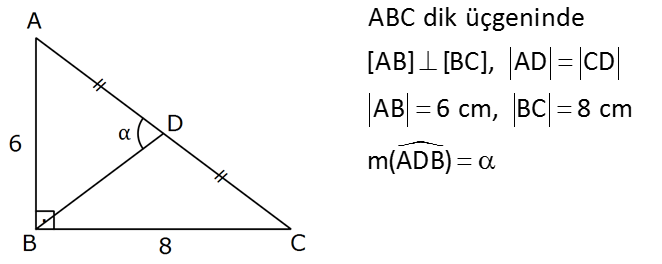
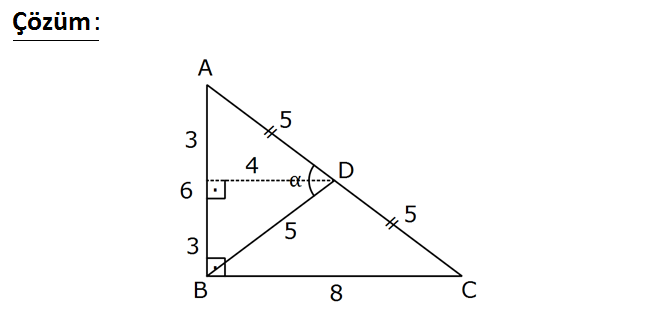
ABC dik üçgeninde [AB] [BC], AD CD AB 6 cm, BC 8 cm m(ADB) Yukarıdaki verilere göre, değeri kaçtır? 7 9 13 24 A) B) C) D) E) 1 25 25 25 25 sinα : Çözüm ABC dik üçgeninde BD kenarortay olduğundan muhteşem üçlüden BD 5 olur. ADC ikizkenar üçgeninde D aç ısından AB ‘ ye diklik indirirsek açısı iki eş açıya bölünür.Oluşan 3 3- 4 – 5 üçgeninden sin , 2 5 4 cos bulunur. 2 5 sin 2.sin .cos 2 2 3 4 24 2. bulunur. 5 5 25 96
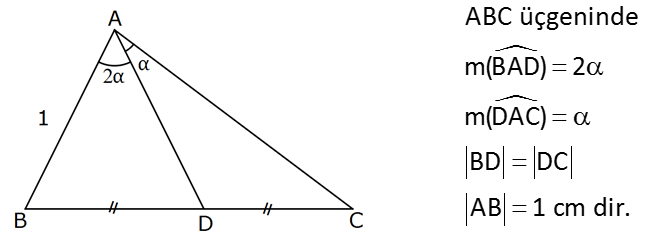
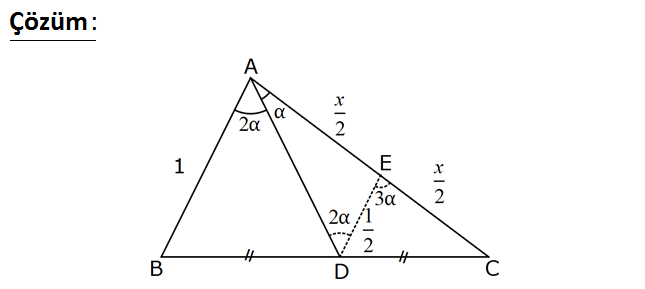
ABC üçgeninde m(BAD) 2 m(DAC) BD DC AB 1 cm dir. Yukarıdaki verilere göre, kaç cm dir? A) 2cos B) cos2 C) sin D AC ) sin2 E) 2tan : Çözüm AC x olsun. AB doğrusuna D noktasından bir DE paraleli çizdiğimizde BC ve AC kenarlarını ortadan ikiy e 1 ayırır ve orta taban olur. DE olur. 2 ADE üçgeninde sinüs teoremi uygulayalım; 1 x 2 2 1 sina sin2a 2 x sina 2 sin2a 1 sina x 2 sina .cosa x 2cosa bulunur.

