Soru Sor sayfası kullanılarak Trigonometri-2 konusu altında Dönüşüm Formülleri ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
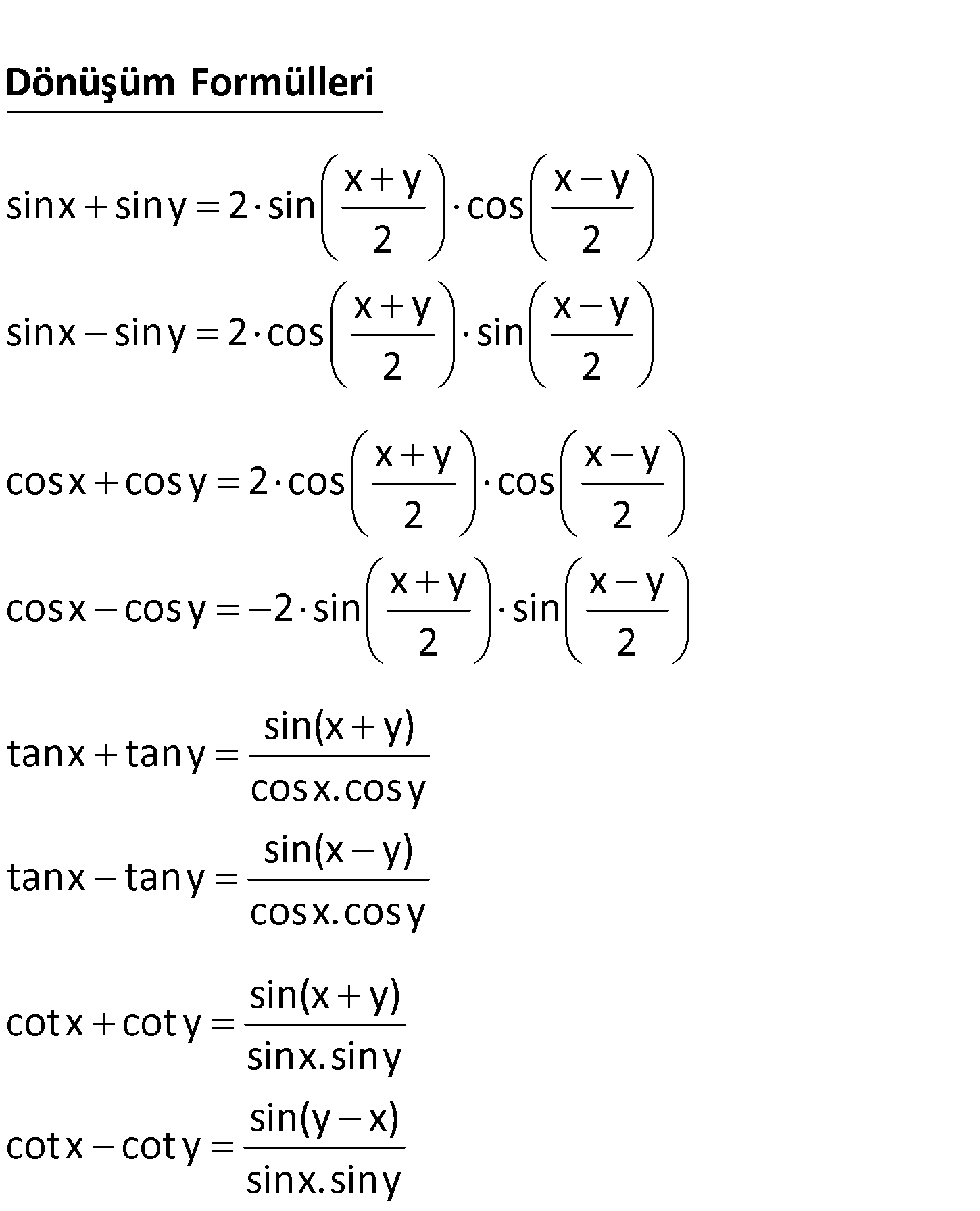
1.SORU

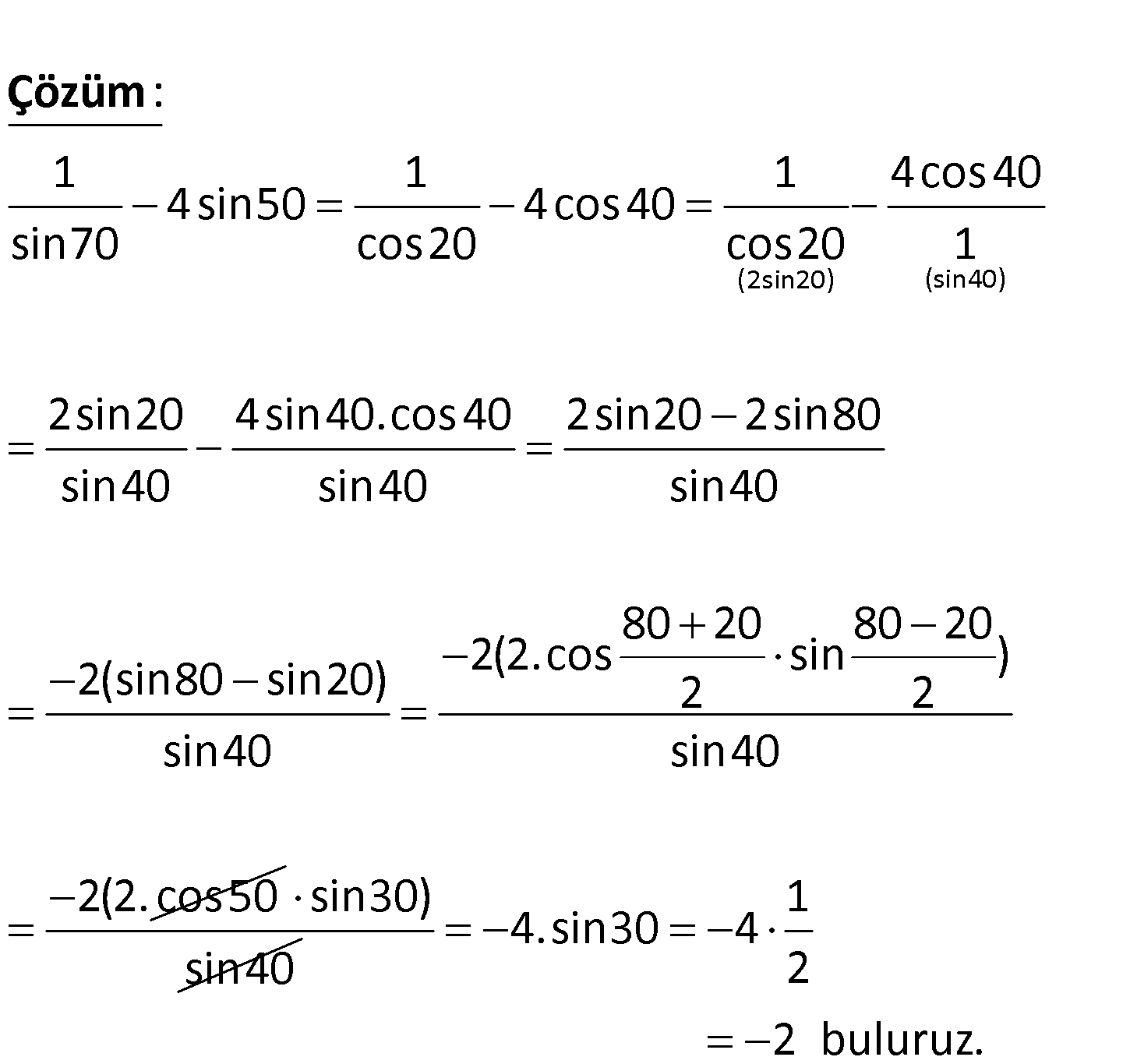
2.SORU
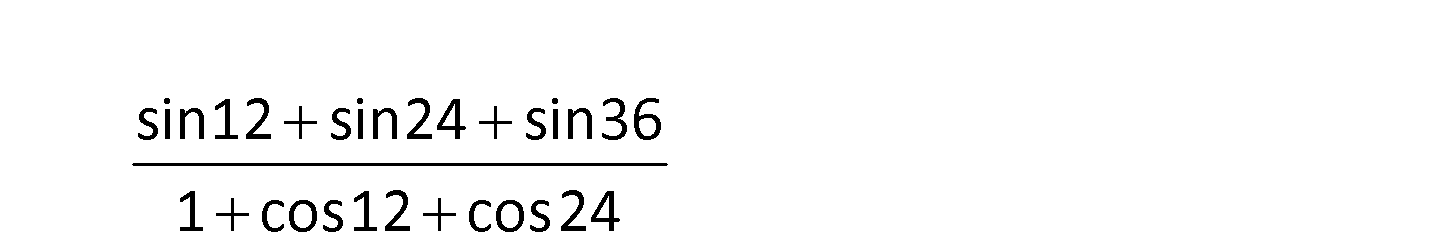

3.SORU


4.SORU
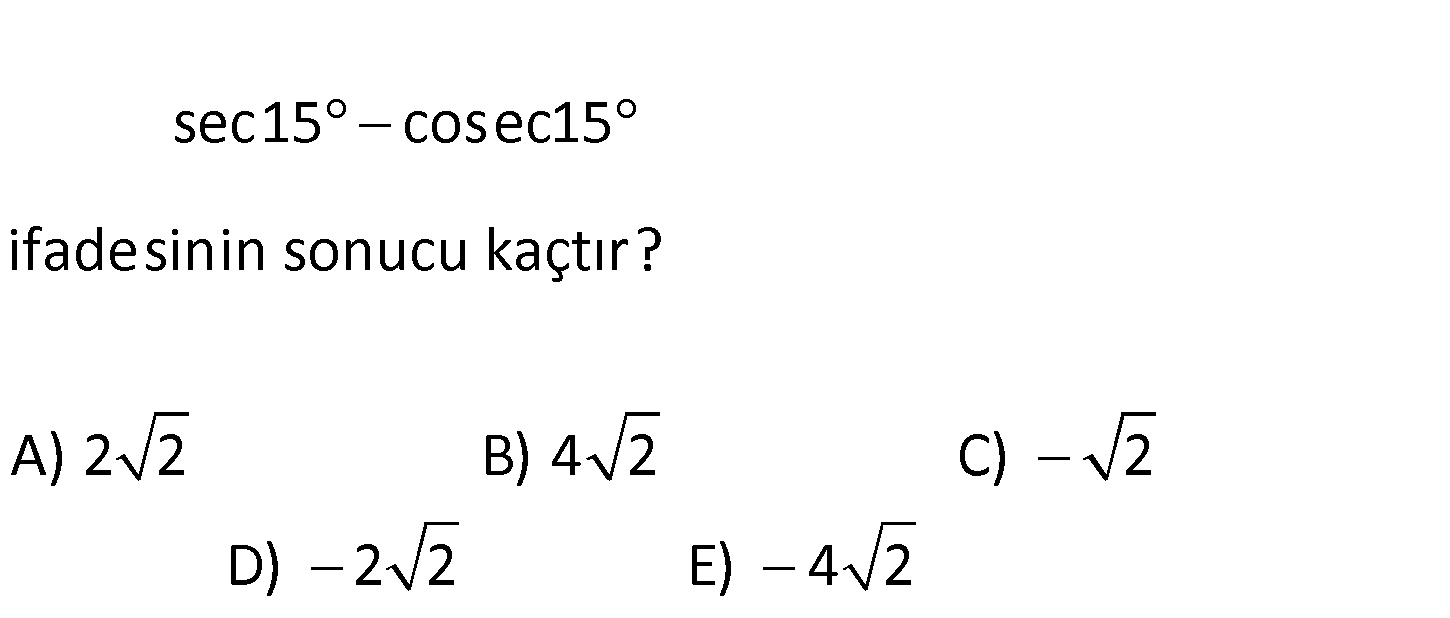
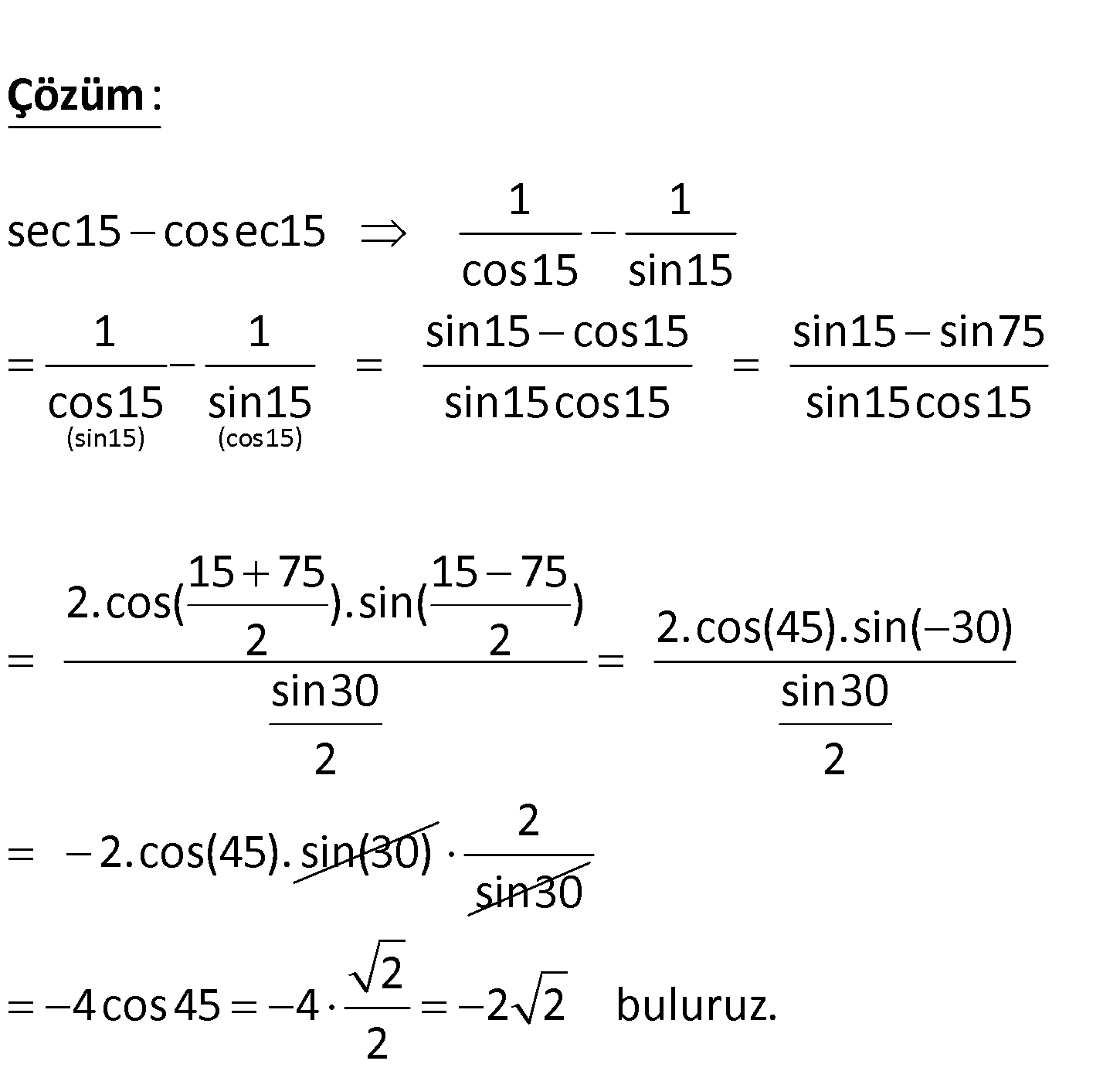
5.SORU

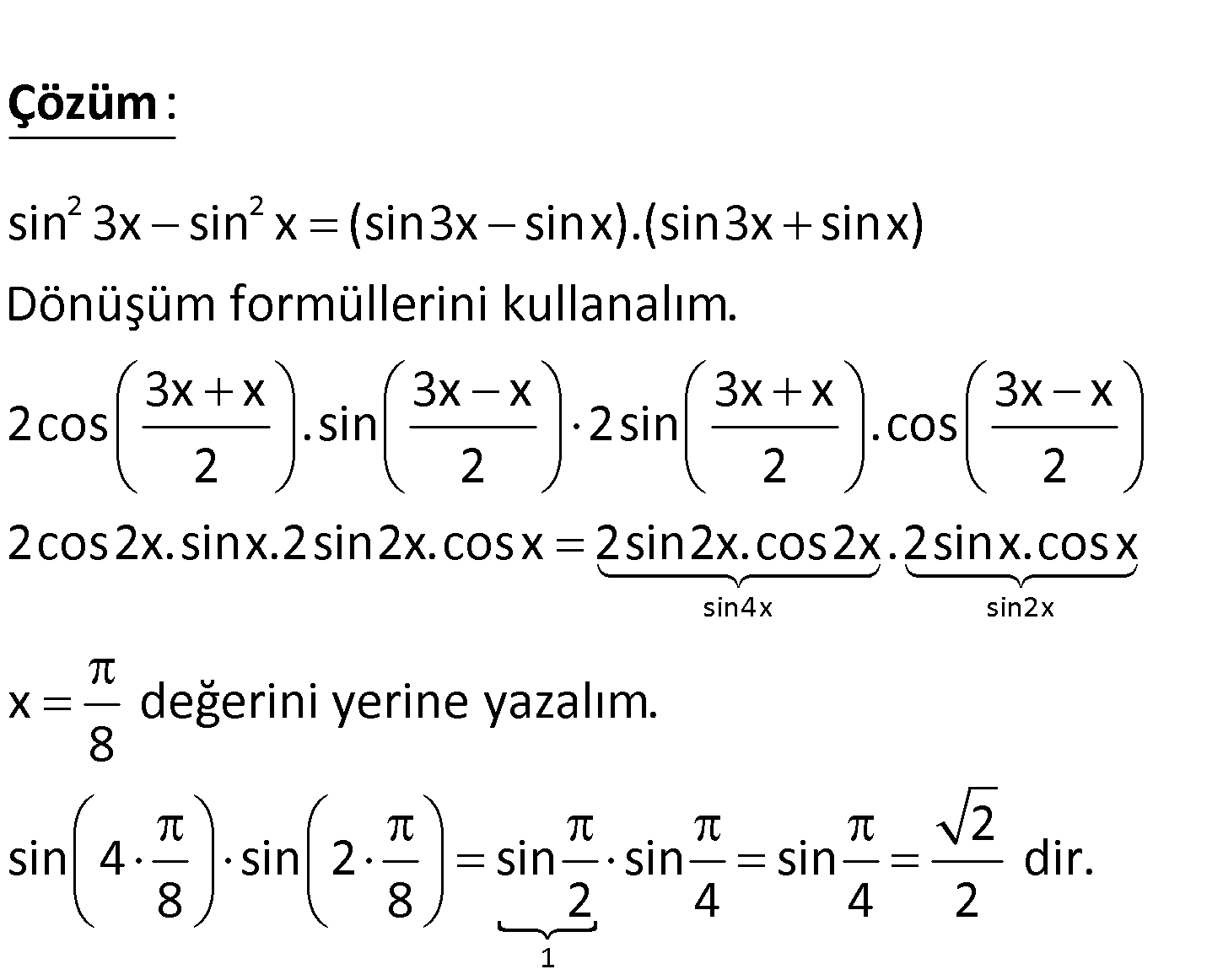
6.SORU
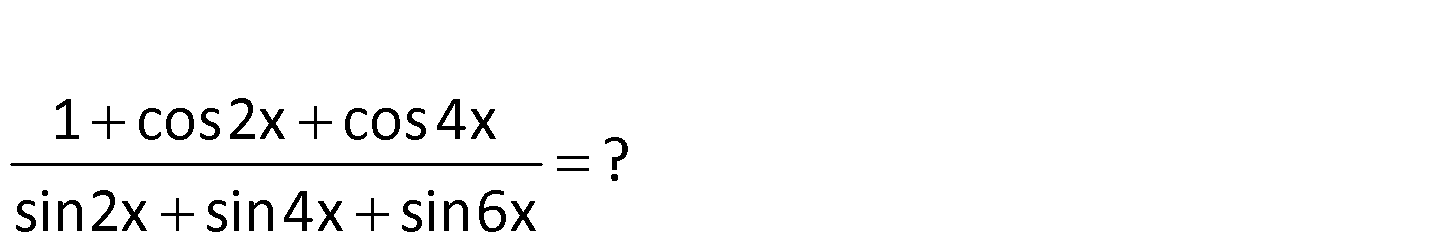

7.SORU


8.SORU

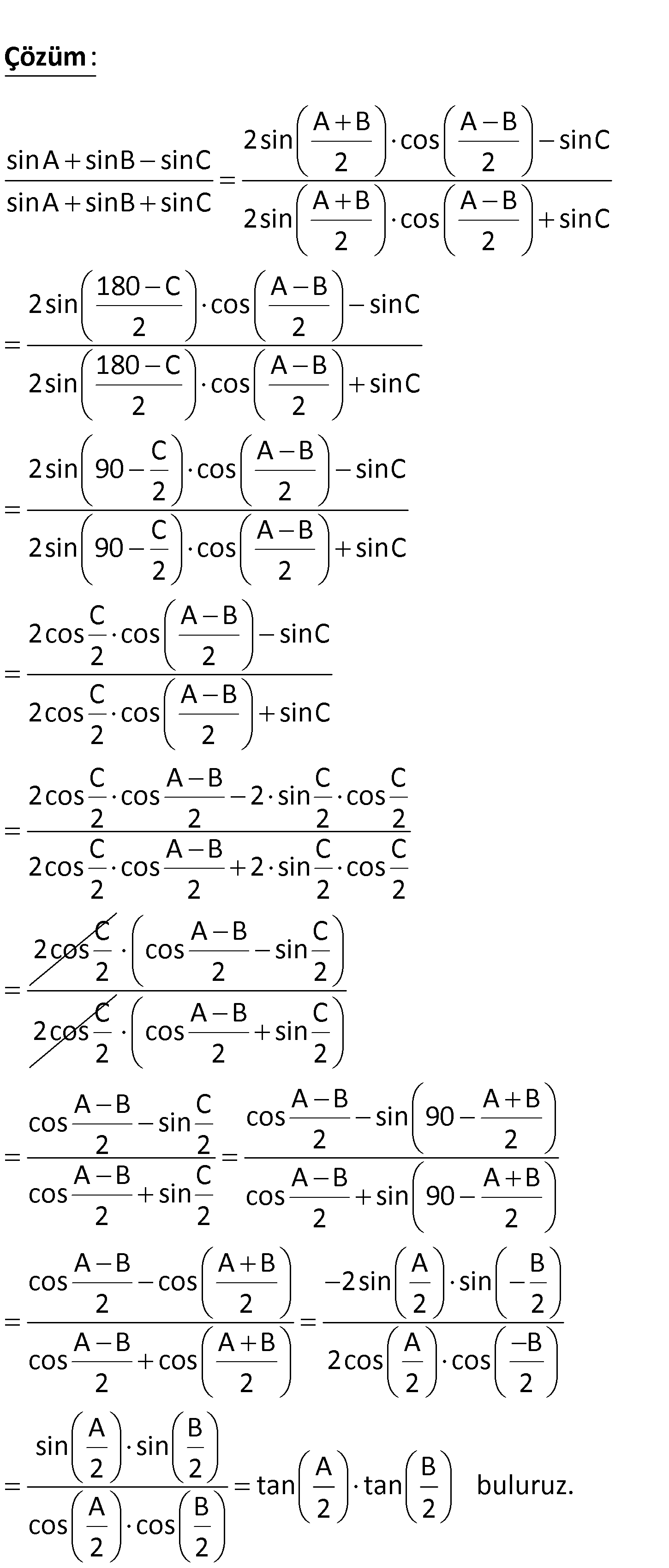
9.SORU
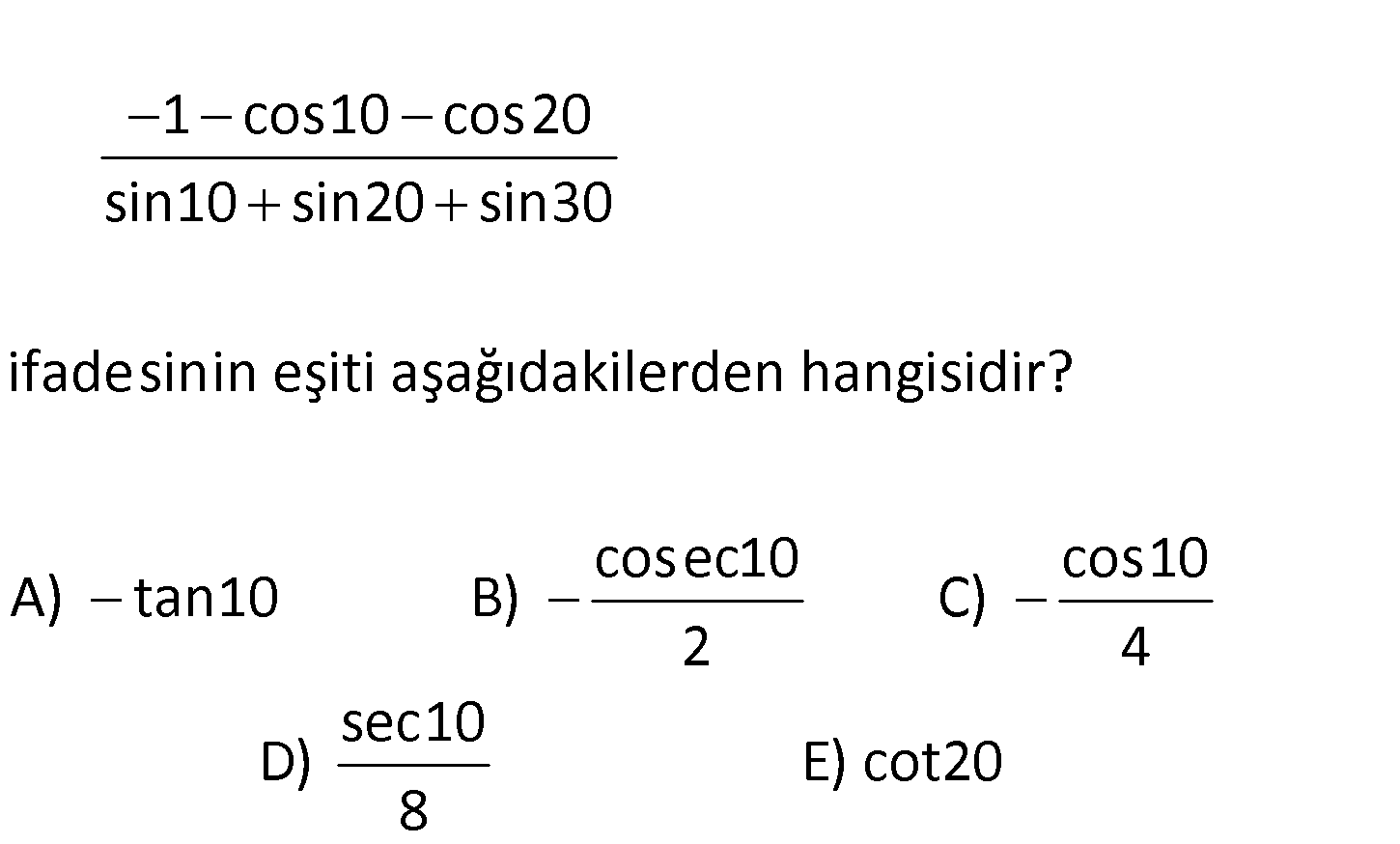

10.SORU

11.SORU
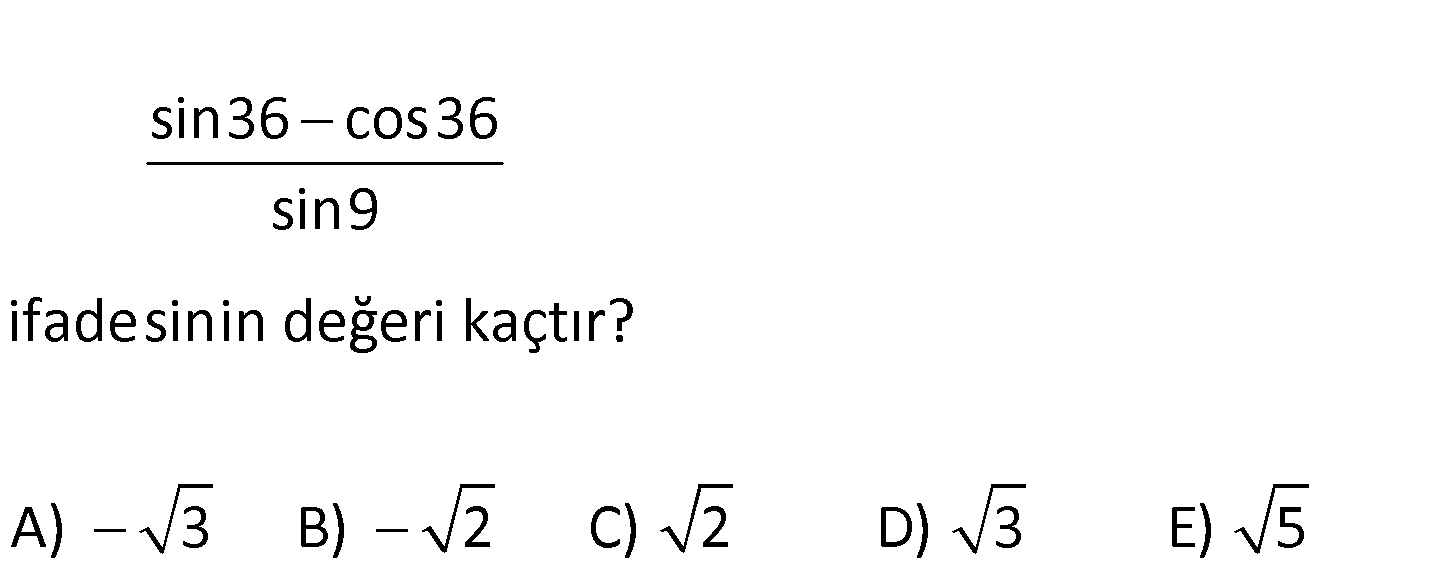
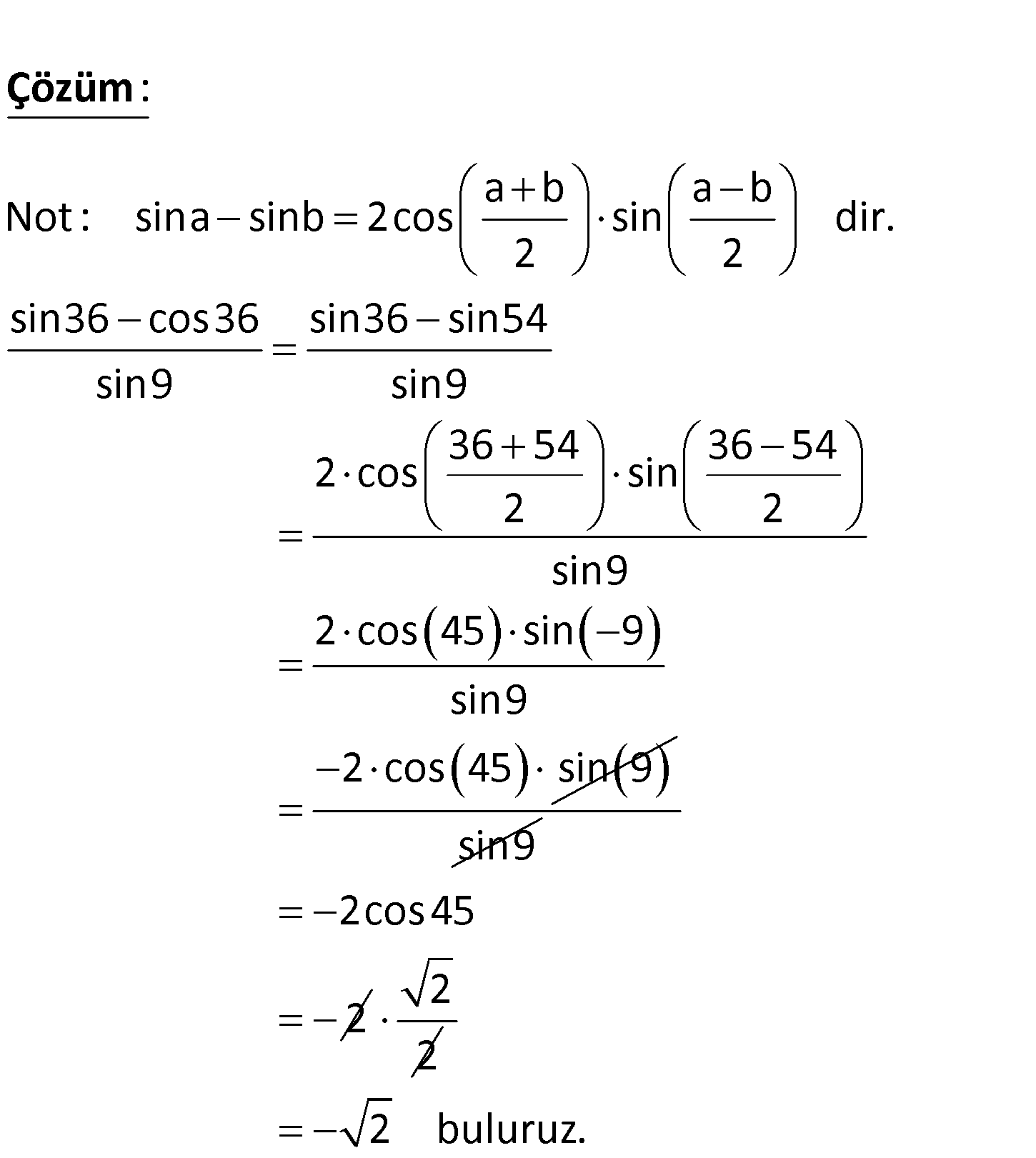
12.SORU
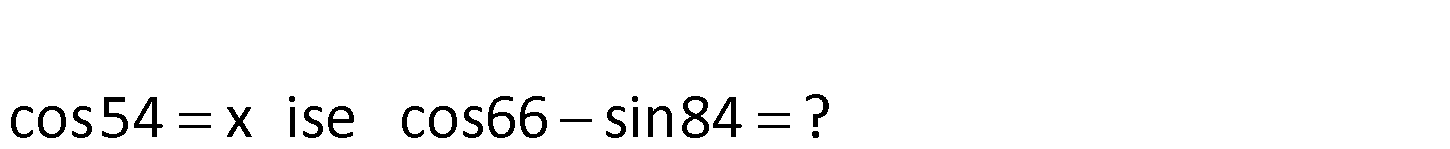

13.SORU

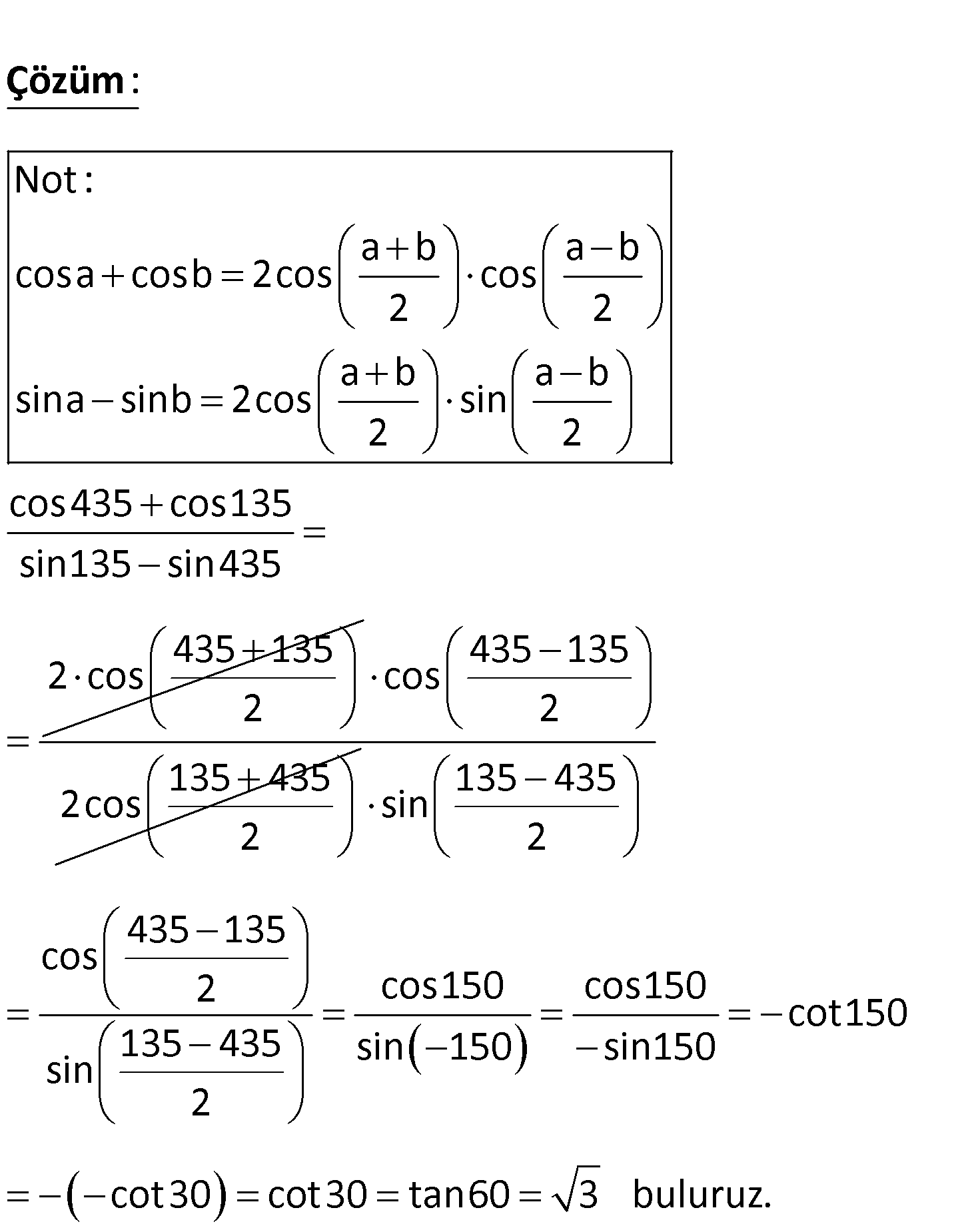
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
1 4sin50 ? sin70 (2sin20) (sin40) : 1 1 1 4cos40 4sin50 4cos40 sin70 cos20 cos20 1 2sin20 4sin40.cos40 2sin sin40 sin40 Çözüm 20 2sin80 sin40 80 20 80 20 2(2.cos sin ) 2(sin80 sin20) 2 2 sin40 sin40 2(2. cos50 sin30) sin40 1 4.sin30 4 2 2 buluruz. 8
sin12 sin24 sin36 1 cos12 cos24 sin12 sin24 sin36 sin12 sin36 sin24 1 cos12 cos24 1 cos12 cos24 12 36 36 12 2 sin cos sin24 2 2 1 c : Çözüm 2 2 os12 2cos 12 1 2 sin24 cos12 sin24 sin24 (2cos12 1) cos12 2cos 12 cos12 (2cos12 1) sin24 (2cos12 1) cos12 (2cos12 1) sin24 cos12 2sin12. cos12 cos12 2sin12 buluruz. 9
x olduğuna göre, 13 cos10x.cosx cos4x cos2x ifadesinin değerini bulunuz. a b a b Not : cosa cosb 2cos( )cos( ) 2 2 Buna göre; cos10x.cosx cos10x.cosx cos4x cos2x 4x 2x 2cos( : )c 2 Çözüm 4x 2x os( ) 2 cos10x.cosx cos10x. cosx 2cos(3x)cos(x) 2cos(3x) cos(x) cos10x ( Soruda 13x verilmiş.) 2cos3x cos3x (Not : cos( a) cosa ) 2cos3x 1 buluruz. 2 20
sec15 cosec15 ifadesinin sonucu kaçtır? A) 2 2 B) 4 2 C) 2 D) 2 2 E) 4 2 (sin15) (cos15) 1 1 sec15 cosec15 cos15 sin15 1 1 sin15 cos15 si cos15 sin15 sin15cos1 : 5 Çözüm n15 sin75 sin15cos15 15 75 15 75 2.cos( ).sin( ) 2 2 2.cos(45).sin( 30) sin30 sin30 2 2 2.cos(45). sin(30) 2 sin30 2 4cos45 4 2 2 buluruz. 2 22
2 2 x olmak üzere, 8 sin 3x sin x ifadesinin değeri kaçtır? 1 1 2 3 3 A) B) C) D) E) 2 3 2 2 3 2 2 sin 3x sin x (sin3x sinx).(sin3x sinx) Dönüşüm formüllerini kullanalım. 3x x 3x 2cos .sin 2 : Çözüm sin4x sin2x 1 x 3x x 3x x 2sin .cos 2 2 2 2cos2x.sinx.2sin2x.cosx 2sin2x.cos2x.2sinx.cosx x değerini yerine yazalım. 8 2 sin 4 sin 2 sin sin sin dir. 8 8 2 4 4 2 29
1 cos2x cos4x ? sin2x sin4x sin6x 1 cos4x 2 2 2 2 1 cos2x cos4x sin2x sin4x sin6x sin 2x cos 2x cos2x cos 2x sin 2x 2x 6 2sin : Çözüm sin2x sin6x 2 x 6x 2x cos sin4x 2 2 2cos 2x cos2x cos2x(2cos2x 1) 2sin4x.cos2x sin4x sin4x(2cos2x 1) cos2x (2cos2x 1) sin4x (2cos2x 1) cos2x sin4x cos2x 2sin2x. cos2x 1 buluruz. 2sin2x 40
2 2 cos84 m olmak üzere, sin 18 sin 12 ifadesinin m türünden değeri aşağıdakilerden hangi sidir? m m A) 3m B) 2m C) m D) E) 2 3 2 2 cos84 m sin6 m dir. sin 18 sin 12 (sin18 sin12)(sin18 sin12) : Çözüm 2.cos15.sin3.2.sin15.cos3 2.sin15.cos15.2.sin3.cos3 sin30.sin6 1 m 2 m buluruz. 2 49
A, B, C bir üçgenin iç açıları olmak üzere, sinA sinB sinC sinA sinB sinC ifadesi aşağıdaki lerden hangisine eşittir? C A C A) tanB B) tan C) tan tan 2 2 2 A B B D) tan tan E) cot 2 2 2 ABAB2sincossinCsinAsinBsinC22ABABsinAsinBsinC2sincoss2:2 ÇözüminC180CAB2sincossinC22180CAB2sincossinC22CAB2sin90cossinC22CAB2sin90cossinC22CAB2coscossinC22CAB2coscossinC22C2cos ABCCcos2sincos2222CABCC2coscos2sincos2222C2cos2 ABCcossin22C2cos2 ABCcossin22ABABABCcossin90cossin2222ABCABABcossincossin902222ABABABcoscos2sinsin2222ABABABcoscos2coscos2222Asin2 BsinAB2tantan buluruz.AB22coscos22 54
1 cos10 cos20 sin10 sin20 sin30 ifadesinin eşiti aşağıdakilerden hangisidir? cose A) tan10 B) c10 cos10 C) 2 4 sec10 D) E) cot20 8 2 2 1 cos10 cos20 1 cos10 (2cos 10 1) sin10 sin20 sin30 sin10 sin30 sin20 cos10 2cos 10 30 2.s : in Çözüm 10 30 10 cos sin20 2 2 cos10(1 2cos10) 2sin20cos10 sin20 cos10(1 2cos10) 2sin20cos10 2sin10.cos10 cos10 (1 2cos10) 2 cos10 1 2cos10 (sin20 sin10) 2(sin20 sin10) 1 2cos10 2.(2sin10.cos10 sin10) 1 2cos10 2.sin10. (2cos10 1) 1 cosec10 dir. 2sin10 2 60
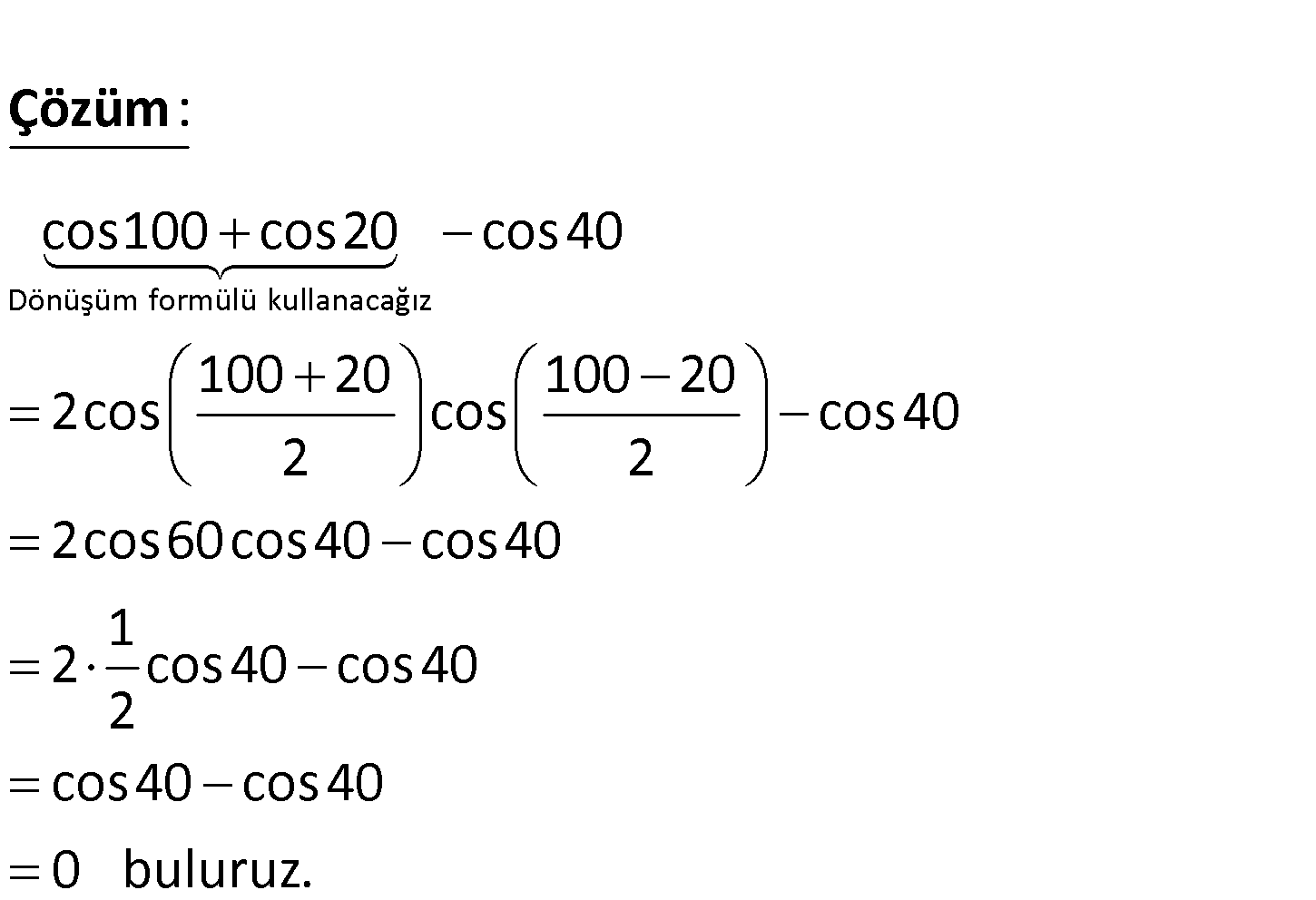
cos100 cos20 cos40 işleminin değerini bulunuz. Dönüşüm formülü kullanacağız cos100 cos20 cos40 100 20 100 20 2cos cos : cos4 2 2 Çözüm 0 2cos60cos40 cos40 1 2 cos40 cos40 2 cos40 cos40 0 buluruz. 75
sin36 cos36 sin9 ifadesinin değeri kaçtır? A) 3 B) 2 C) 2 D) 3 E) 5 a b a b Not : sina sinb 2cos sin dir. 2 2 sin36 cos36 sin36 sin54 sin9 sin9 : Çözüm 36 54 36 54 2 cos sin 2 2 sin9 2 cos 45 sin 9 sin9 2 cos 45 sin 9 sin9 2cos45 2 2 2 2 buluruz. 86
cos54 x ise cos66sin84 ? : a b a b Not : cosa cosb 2 sin sin dir. 2 2 cos66 sin84 cos66 cos6 66 6 2 si n 2 Çözüm 66 6 sin 2 2 sin 36 sin 30 1 2sin36 2 sin36 cos54 x ise sin36 x tir. x buluruz. 87
cos435 cos135 sin135 sin435 ifadesinin en sade hali aşağıdakilerden hangisidir? A) 2 3 B) 3 2 3 3 C) 3 D) E) 2 3 Not : a b a b cosa cosb 2cos cos 2 2 a b a b sina sinb 2cos sin 2 2 cos435 cos13 : Çözüm 5 sin135 sin435 435 135 2 cos 2 435 135 cos 2 135 435 2cos 2 135 435 sin 2 435 135 cos 2 cos150 cos150 cot150 135 435 sin 150 sin150 sin 2 cot30 cot30 tan60 3 buluruz. 89

