Soru Sor sayfası kullanılarak Trigonometri-1 konusu altında Ters trigonometrik fonksiyonlar ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…

1.SORU
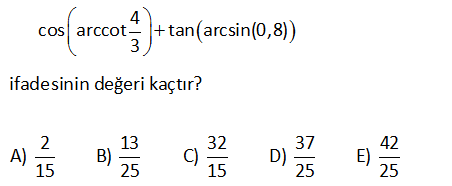

2.SORU


3.SORU
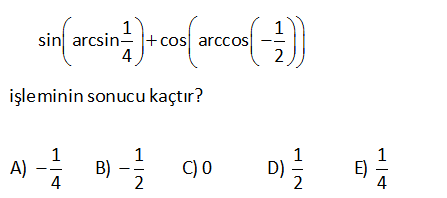

4.SORU
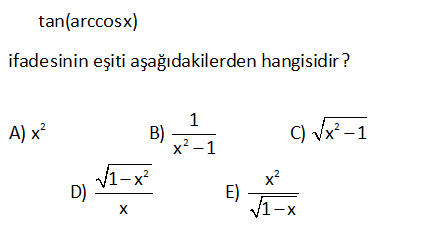

5.SORU
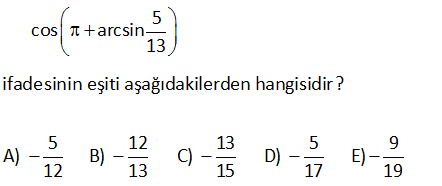

6.SORU


7.SORU


8.SORU
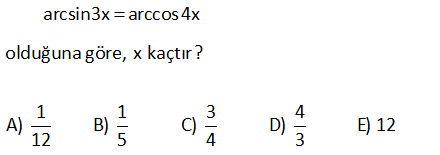

9.SORU
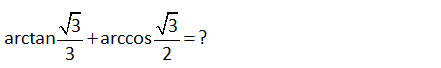
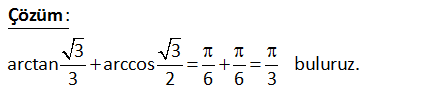
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
: [ 1, 1] , 2 2 y arcsinx x siny : [ 1, 1] [0, ] y arccosx x ??NOT : arcsin arccos cos y : R , 2 2 y arctanx x tany : R 0, y arccotx x cot y ?arctan arccot 4 cos arccot tan arcsin(0,8) 3 ifadesinin değeri kaçtır2 13 32 37 42 A) B) C) D) E) 15 25 15 25 25 Soruda verilen oranlar 3- 4 – 5 üçgeninde yer alan oranlardır. Bu yüzden 3 – 4 – 5 üçgeni çize : rek, Çözüm soruyu kolaylıkla çözebiliriz. Üçgenden; 4 4 cotx arccot x tir. 3 3 4 siny 0,8 arcsin(0,8) y dir. 5 Buna göre soruyu çöze (3) (5) lim; 4 cos arccot tan(arcsin(0,8)) 3 cosx tany 4 4 12 20 32 buluruz. 5 3 15 15 15 36
f(x) cos(arcsinx) 3 f f 10 5 olduğuna göre, işleminin sonucu 12 f 13 kaçtır2 A) B) 15 13 32 37 42 C) D) E) 25 15 25 25 : Çözüm Üçgenlerden yararlanarak soruyu çözelim. 3 3 f f(0) cos arcsin cos arcsin0 5 5 12 f cos a 13 12 rcsin 13 4 1 cos x cos 0 1 5 5 cos y 5 5 13 13 1 13 13 buluruz. 5 5 25 37
1 1 sin arcsin cos arccos 4 2 işleminin sonucu kaçtır1 1 1 1 A) B) C) 0 D) E) 4 2 2 4 ?Bir fonksiyonun tersinin tersi , yine kendisidir. Bu sebeple; 1 1 sin arcsin cos arccos 4 2 : Çözüm -2 1 1 1 2 1 buluruz. 4 2 4 4 4 38
2 2 2 tan(arccosx) ifadesinin eşiti aşağıdakilerden hangisidir1 A) x B) C) x 1 x 1 2 2 1 x x D) E) x 1 x : Çözüm Kosinüsü x olan bir a açısını üçgende gösterelim. cosa x arccosx a dır. a açısının karşısındaki 2 2 kenarı pisagor teoreminden 1 x şeklinde yazabiliriz. Buna göre; 1 x tan(arccosx) tana buluruz. x 39
5 cos arcsin 13 ifadesinin eşiti aşağıdakilerden hangisidir5 12 13 5 A) B) C) D) 12 13 15 ?9 E) 17 19 : Çözüm III. bölgede kosinüs ( 5 arcsin x olsun. (Üçgende gösterildiği gibi) 13 5 cos arcsin cos ( x) 13 ?) 12 cosx buluruz. 13 40
1 cos arctan 2 3 ifadesinin eşiti aşağıdakilerden hangisidir10 10 A) 10 B) C) 10 3 2 10 3 10 D) E) 5 5 : Çözüm II. bölgede kosinü 1 arctan x olsun. (Üçgende gösterildiği gibi) 3 1 cos arctan cos x 2 3 2 s ( ) -10 1 10 sinx buluruz. 10 10 41
x ?arccos(sinx) ? : Çözüm a sinx dir. c a arccos sinx arccos 90 x dir. Buna göre; c x arccos(sinx) x 90 x 90 buluruz. 50
arcsin3x arccos4x olduğuna göre, x kaçtır1 1 3 4 A) B) C) D) E) 12 12 5 4 3 arcsin3x arccos4x a açısına eşit olsun. Bu a açısının sinüsü 3x, kosinüsü de 4x : olmalıd Çözüm ır. Bunu dik bir üçgen çizip gösterelim. Burada bir 3- 4 – 5 üçgeni oluştu ve hipotenüs 5x oduğundan; 1 5x 1 x buluruz. 5 ?
3 3 arctan arccos 3 2 3 3 arctan arccos buluruz. 3 2 6 6 3 : Çözüm 9

