Soru Sor sayfası kullanılarak Trigonometri-1 konusu altında Sinüs Teoremi, Sinüs ile kenarlar arasındaki oran ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

2.SORU


3.SORU

4.SORU

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
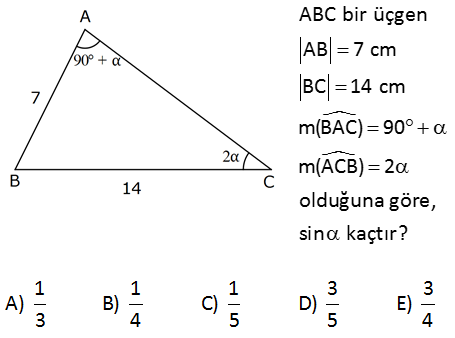
ABC bir üçgen AB 7 cm BC 14 cm m(BAC) 90 m(ACB) 2 olduğuna göre, sin kaçtır 1 1 1 3 3 A) B) C) D) E) 3 4 5 5 4 7 14 (Sinüs teoremi) sin2 sin(90 ) 7 14 sin2 c s 7 : o Çözüm 2sincos14 2 cos1 4sin 1 sin buluruz. 4 14
Kenar uzunlukları a, b, c olan bir ABC üçgeninin çevresi 24 cm dir. sinA sinB 3sinC oldu ğuna göre, c kenarının uzunluğu kaç cm dirA) 3 B) 4 C) 6 D) 8 E) 10 Üçgende sinüs teoremine göre; a b c dir. sinA sinB sinC Payları kendi arasında, paydaları da ke : Çözüm ndi arasında toplarsak orantı değişmez. Yani; a b c şeklinde kurabiliriz. sinA sinB sinC a b c 24 ise a b 24 c dir. sinA sinB 3sinc verilmiş. Buna göre; 24 c 3 sinc c sinC 24 c 3c 24 4c c 6 buluruz. 19
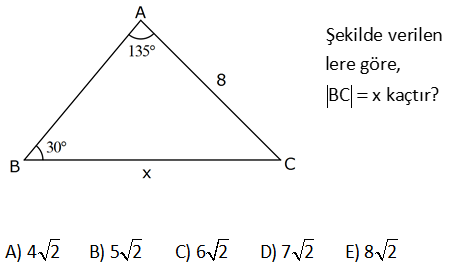
Şekilde verilen lere göre, BC x kaçtırA) 4 2 B) 5 2 C) 6 2 D) 7 2 E) 8 2 Açının sinüsü ile karşısındaki kenarın oranı bir üçgende aynıdır. 8 x oranı sa sin30 sin : 135 Çözüm ğlanmalıdır. 8 x 2 8 1 2 2 2 2 x 2 x 8 2 buluruz. 22
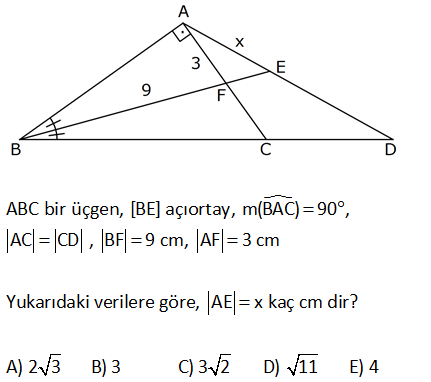
ABC bir üçgen, [BE] açıortay, m(BAC) 90 , AC CD , BF 9 cm, AF 3 cm Yukarıdaki verilere göre, AE x k aç cm dirA) 2 3 B) 3 C) 3 2 D) 11 E) 4 2 2 |AB| 9 3 81 9 72 6 2 dir. Aynı olan açıları harflendirelim. 2a 2b 90 a b 45 dir. m(AEB) : a Çözüm b 45 dir. ABE üçgeninde kenarlar arasında sinüs teoremini uygularsak; x 6 2 x sina sin45 3 9 3 6 2 2 3x 12 2 x 4 buluruz. 25

