Soru Sor sayfası kullanılarak Trigonometri-1 konusu altında Kosinüs Teoremi, Üçgende bir kenarı kosinüs yardımıyla bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
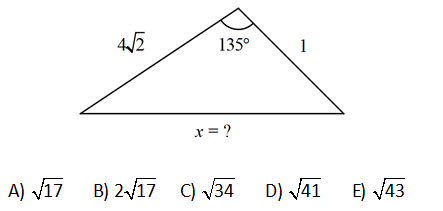

2.SORU


3.SORU

4.SORU

5.SORU
6.SORU


7.SORU


8.SORU
9.SORU
10.SORU

11.SORU

12.SORU
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
Kosinüs Teoremi, Üçgende bir kenarı kosinüs yardımıyla bulma
A) 17 B) 2 17 C) 34 D) 41 E) 43 ?2 2 2 2 2 2 2 2 x 4 2 1 2.4 2.1.cos135 x 32 1 8 2 cos135 x 32 1 8 2( cos45) 2 x 32 1 8 2 ( ) 2 x 32 1 8 x 41 x 41 : Çözüm buluruz. 2
2 2 2 Kenar uzunlukları a, b ve c birim olan bir ABC üçge – ninde, b c a 3ac olduğuna göre, m( A) m(C) toplamı kaç derecedirA) 30 B) 60 C) 90 D) 120 E) 150 2 2 2 2 2 2 2 2 2 cosB o Kosinüs Teoremi: b a c 2accosB b c a 3ac 3 b c a 2ac 2 3 cosB m(B) 30 2 m(A) m( : Çözüm o o 30 o B) m(C) 180 m(A) m(C) 150 buluruz. 3
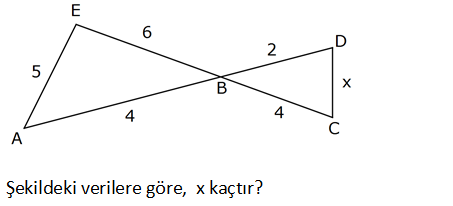
Şekildeki verilere göre, x kaçtır : Çözüm 2 2 2 İki üçgende açıları ortaktır. İki üçgende aynı açıya göre kosinüs teoremi uygulayalım. 5 6 4 2. 2 2 2 2 6.4.cos 25 36 16 48cos 25 52 48cos 27 9 cos dır. 48 16 x 2 4 2.2.4.cos x 4 16 16 9 16 11 x 11 buluruz. 15
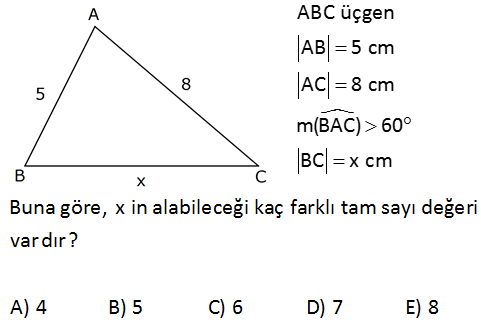
ABC üçgen AB 5 cm AC 8 cm m(BAC) 60 BC x cm ?Buna göre, x in alabileceği kaç farklı tam sayı değeri vardırA) 4 B) 5 C) 6 D) 7 E) 8 2 2 2 2 2 m(BAC) 60 olsaydı; x 5 8 2.5.8.cos60 x 25 64 40 x 49 x 7 olurdu. m(BAC) 60 : x 7 dir. Ay Çözüm rıca x 5 8 x 13 tür. Buna uygun x değerleri 8,9,10,11,12 5 tane 16
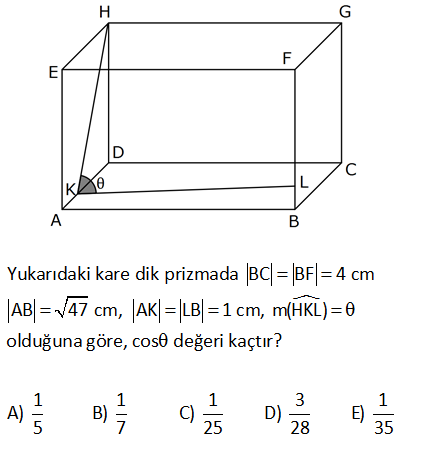
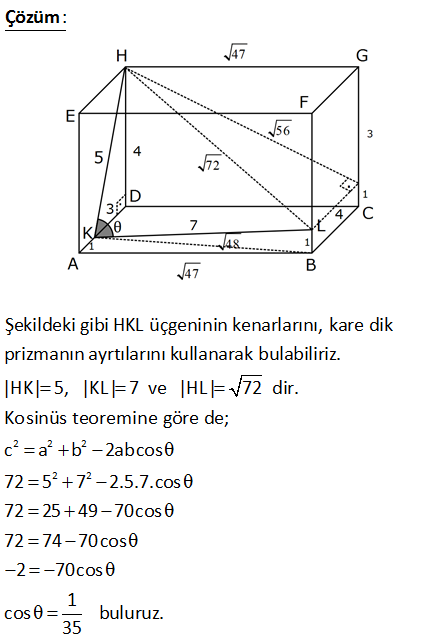
Yukarıdaki kare dik prizmada BC BF 4 cm AB 47 cm, AK LB 1 cm, m(HKL) olduğuna göre, cos değeri ka çtır1 1 1 3 1 A) B) C) D) E) 5 7 25 28 35 : Çözüm Şekildeki gibi HKL üçgeninin kenarlarını, kare dik prizmanın ayrtılarını kullanarak bulabiliriz. |H 2 2 2 2 2 K| 5, |KL| 7 ve |HL| 72 dir. Kosinüs teoremine göre de; c a b 2abcos 72 5 7 2.5.7.cos 72 25 49 70cos 72 74 70cos 2 70cos 1 cos buluruz. 35 17
3 3 3 2 Bir ABC üçgeninin kenarları arasında, b c a a b c a bağıntısı olduğuna göre, m(A) ka ç derecedirA) 30 B) 45 C) 50 D) 60 E) 120 3 3 3 b c a b : c a Çözüm 2 3 3 3 a b c ?a 2 2 3 a b a c ?a 3 3 2 b c a b c b c 2 2 2 b ?bc c a b c 2 2 2 2 2 2 2 2 a b c bc a b c 2b.c.cosA cosinüs teoremi b c 2 2 ?bc b c 2b.c.cosA b.c ?2b.c. cosA 1 cosA dir. 2 A 60 bulunur. 18
2 Kenar uzunlukları a, b, c olan bir ABC üçgeninde c m(C) 120 dir. a b 3 ab olduğuna göre, ab oran ı kaçtır5 3 1 A) 8 B) 6 C) D) E) 2 2 4 2 2 2 2 2 2 2 2 2 2 2 2 c a b 2abcos(C) (kosinüs teoremi) c a b 2abcos(120) 1 c a b 2ab 2 c a b a : b Çözüm 2 2 2 2 (a b) 2 2 2 2 2 2 2 (ab ekleyip, çıkaralım) c a b 2ab ab c (a b) ab c (3 ab) ab c 9ab ab c 8ab c 8 buluruz. ab 12
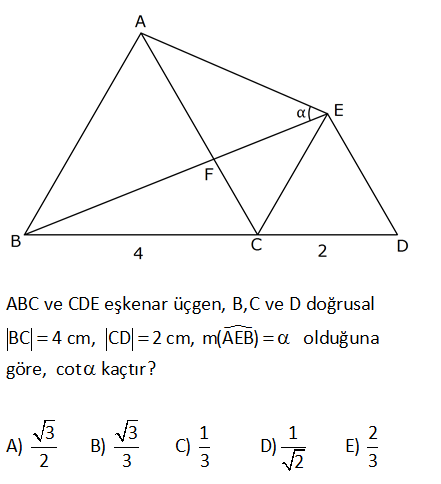
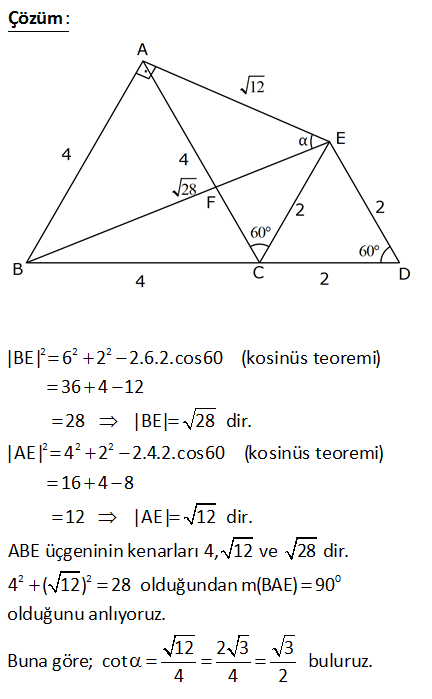
ABC ve CDE eşkenar üçgen, B,C ve D doğrusal BC 4 cm, CD 2 cm, m(AEB) olduğuna göre, cot kaçtır 3 3 1 1 2 A) B) C) D) E) 2 3 3 2 3 : Çözüm 2 2 2 2 2 |BE| 6 2 2.6.2.cos60 (kosinüs teoremi) 36 4 12 28 |BE| 28 dir. |AE| 4 2 2 2 0 2 2.4.2.cos60 (kosinüs teoremi) 16 4 8 12 |AE| 12 dir. ABE üçgeninin kenarları 4, 12 ve 28 dir. 4 ( 12) 28 olduğundan m(BAE) 90 olduğunu anlıyoruz. 12 2 3 3 Buna göre; cot 4 4 buluruz. 2 13
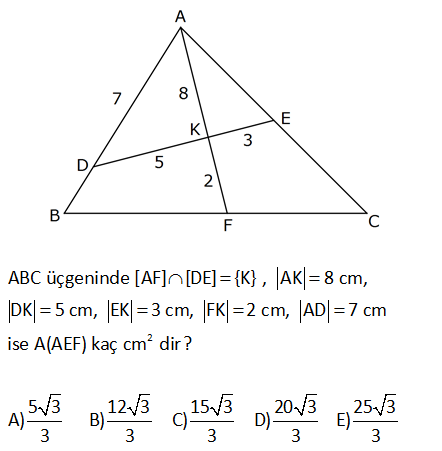
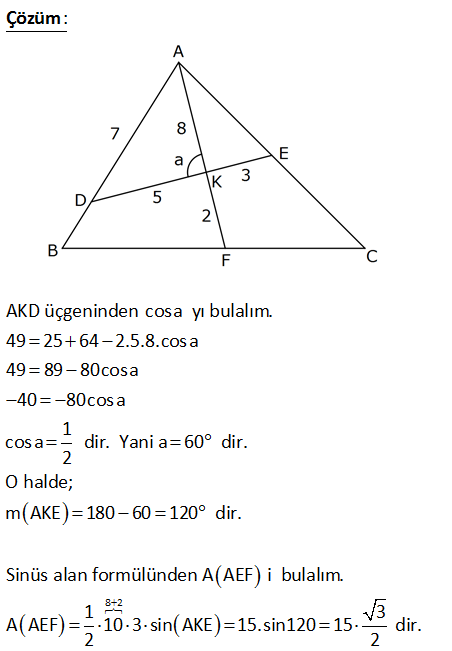
2 ABC üçgeninde [AF] [DE] {K} , AK 8 cm, DK 5 cm, EK 3 cm, FK 2 cm, AD 7 cm ise A(AEF) kaç cm dirA) 5 3 12 3 15 3 20 3 25 3 B) C) D) E) 3 3 3 3 3 : Çözüm AKD üçgeninden cosa yı bulalım. 49 25 64 2.5.8.cosa 49 89 80cosa 40 80cosa 1 cosa dir. Yani a 60 2 8 2 dir. O halde; m AKE 180 60 120 dir. Sinüs alan formülünden A AEF i bulalım. 1 3 A AEF 10 3 sin AKE 15.sin120 15 dir. 2 2 20
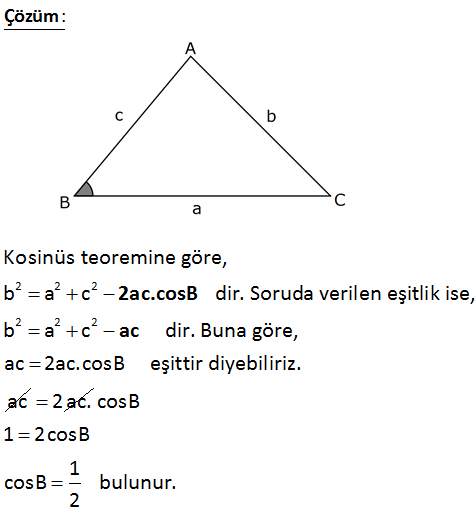
2 2 2 Bir ABC üçgeninde kenar uzunlukları a, b ve c dir. b a c ac olduğuna göre, cosB kaçtı r1 3 1 3 7 A) B) C) D) E) 4 2 2 3 8 : Çözüm 2 2 2 2 2 2 Kosinüs teoremine göre, b a c dir. Soruda verilen eşitlik ise, b a c dir. Buna göre, ac 2ac.cosB eşittir diyebiliriz. ac 2ac.cosB ac 2 ac. cosB 1 2cosB 1 cosB bulunur. 2 23
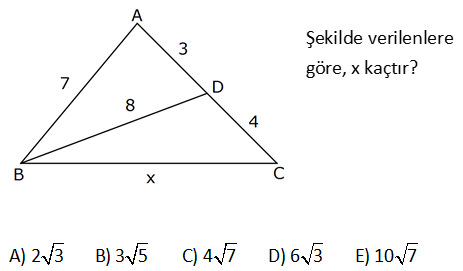
Şekilde verilenlere göre, x kaçtırA) 2 3 B) 3 5 C) 4 7 D) 6 3 E) 10 7 2 2 2 ABD üçgeninde kosinüs teoremini uygulayalım. 8 7 3 2.3.7.cosA 64 49 9 42.cosA 64 58 42.cos 6 : A Çözüm 2 2 2 2 42.cosA 1 cosA dir. 7 ABC üçgeninde kosinüs teoremini uygulayalım. x 7 7 2.7.7.cosA x 49 49 2 7 7 1 7 2 2 x 98 14 x 112 x 4 7 buluruz. 24
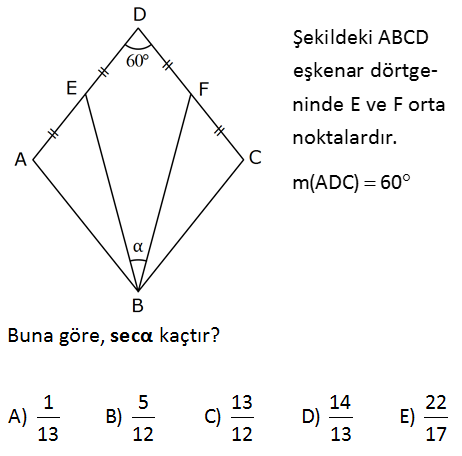
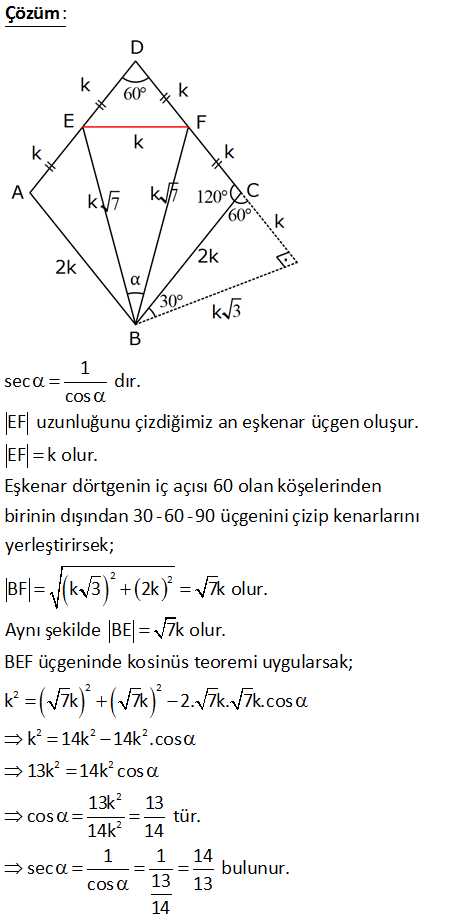
Şekildeki ABCD eşkenar dörtgeninde E ve F orta noktalardır. m(ADC) 60?Buna göre, kaçtır1 5 13 14 22 A) B) C) D) E) 13 12 12 13 17 sec : Çözüm 2 2 1 sec dır. cos EF uzunluğunu çizdiğimiz an eşkenar üçgen oluşur. EF k olur. Eşkenar dörtgenin iç açısı 60 olan köşelerinden birinin dışından 30 – 60 – 90 üçgenini çizip kenarlarını yerleştirirsek; BF k 3 2k 2 2 2 2 2 2 2 2 2 2 7k olur. Aynı şekilde BE 7k olur. BEF üçgeninde kosinüs teoremi uygularsak; k 7k 7k 2. 7k. 7k.cos k 14k 14k .cos 13k 14k cos 13k 13 cos tür. 14k 14 1 1 14 sec bulunur. cos 13 13 14 10

