Soru Sor sayfası kullanılarak Trigonometri-1 konusu altında sinüsün maksimum değeri, kosinüsün maksimum değeri ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU


5.SORU


6.SORU
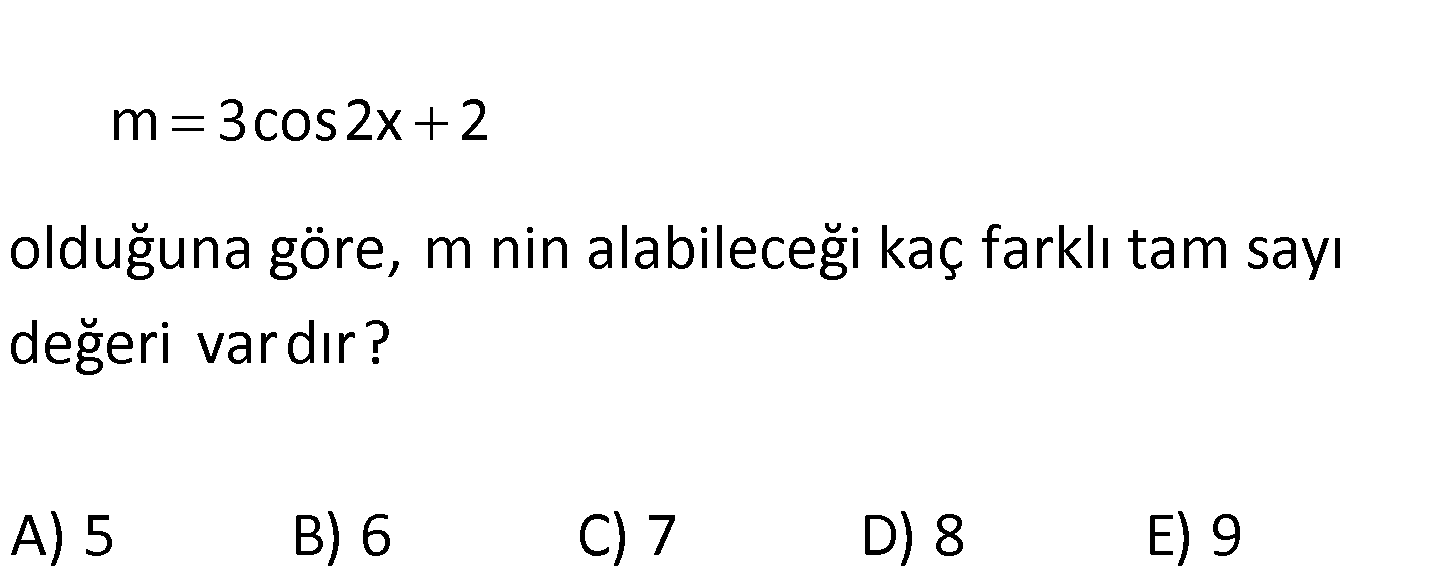

7.SORU


8.SORU


9.SORU


10.SORU

11.SORU

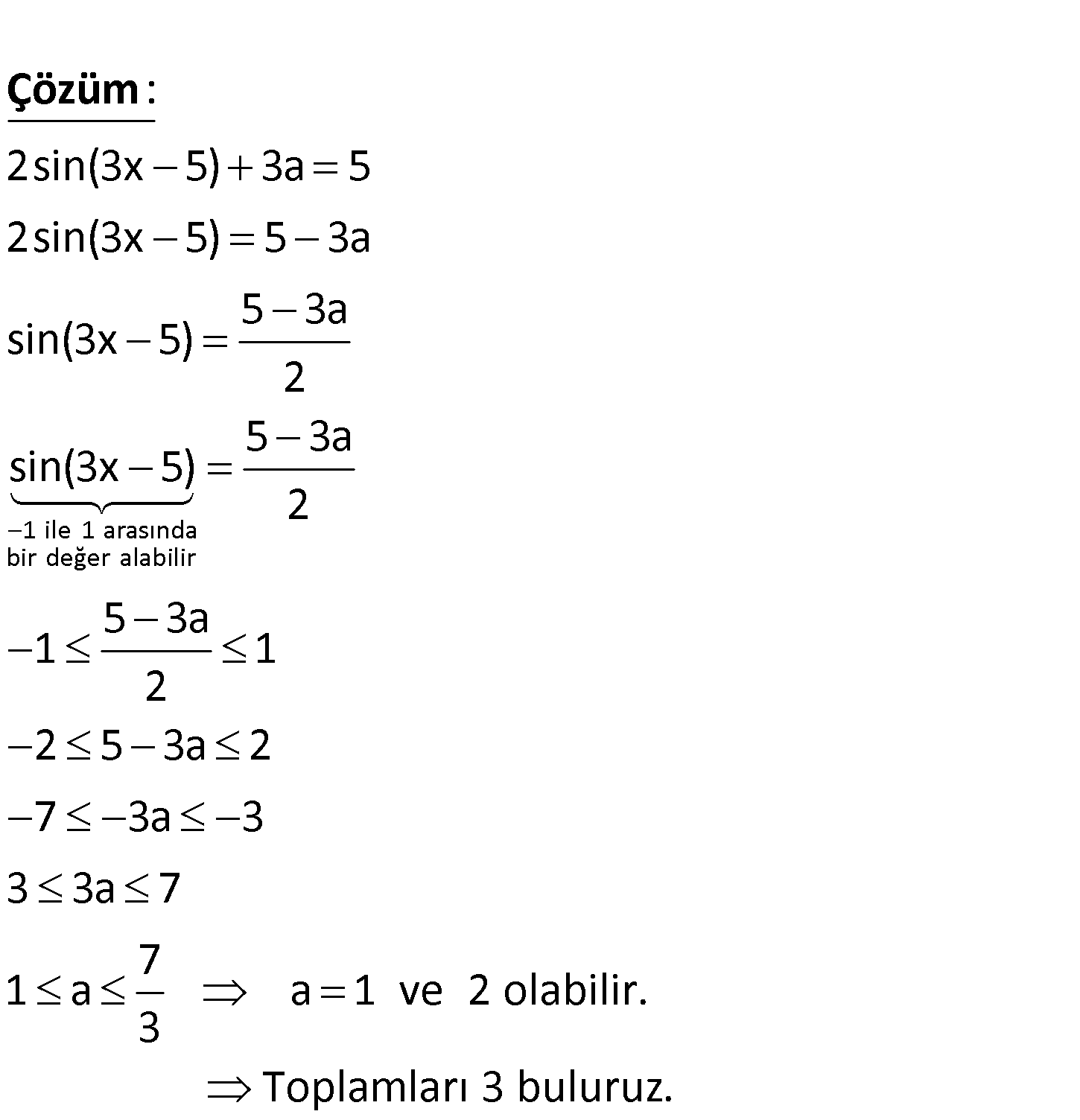
12.SORU


13.SORU
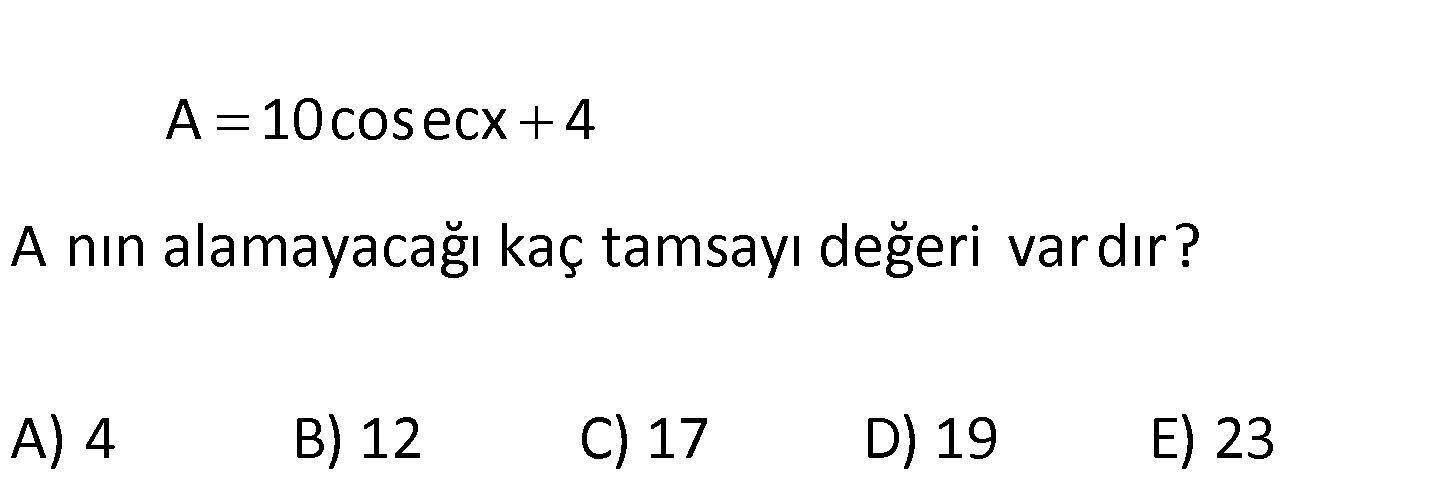

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3cosx 7 f(x) 2 olduğuna göre, f(x) in görüntü kümesindeki tam sayıların toplamı kaçtır? A) 2 B) 8 C) 12 D) 14 E) 16 www.matematikkolay.net cosx ve sinx fonksiyonları 1 ve 1 arasında değer alabilir. Bunların dışına çıkamazl : ar. Bu Çözüm 1 1 sebeple; f(x)’in en küçük değeri; 3cosx 7 3 7 4 2 dir. 2 2 2 f(x)’in en büyük değeri; 3cosx 7 3 7 10 5 tir. 2 2 2 2 f(x) 5 2 3 4 5 14 buluruz. 54
A 2cosx 3 olduğuna göre, A nın alabileceği değerlerini bulunuz . tam sayı cosx ve sinx fonksiyonları 1 ve 1 arasında değer alabilir. Bunların dışına çıkamazl : ar. Bu Çözüm 1 1 sebeple; A’nın en küçük değeri; 2 3 1 dir. A’nın en büyük değeri; 2 3 5 tir. Buna gör A 2cosx 3 A 2co e, A 1,2,3,4,5 olabi s i . 3 l r x 56
olduğuna göre, a kaç farklı tam sayı değ 2 5 eri alabilir sin 3a 7 3 ? A) 3 B) 4 C) 5 D) 6 E) 7 www.matematikkolay.net cosx ve sinx fonksiyonları 1 ve 1 arasında değer alabilir. Bunların dışına çıkamazl : ar. 5.s Çözüm 1 ile 1 arasında 2 in 3a 7 3 5 3a 7 5 yazabiliriz. Her tarafa 7 ekleyelim. 2 3a 12 olur. 3’e bölelim. 2 a 4 olur. 3 Buna göre; a 1,2,3,4 tam sayı değerlerini alabilir. 4 fark lı değer 58
2 K 5sin 4x 3cos3y sayısının alabileceği en büyük ve en küçük değerle – rin toplamı kaçtır? A) 2 B) 0 C) 3 D) 5 E) 12 sinüs ve kosinüs 1 ve 1 arasında değer alabilen fonksiyonlardır. sinüsün karesi negat : if ola Çözüm 2 1 1 2 0 1 mayacağı için 0 ile 1 arasında değerler alabilir. Buna göre, En büyük K 5sin 4x 3cos3y 5 3 8 dir. En küçük K 5sin 4x 3cos3y 0 3 3 tür. Toplamları 8 3 5 buluruz. 65
m 2sinx 5 olduğuna göre, m nin alabileceği tam sayı değerlerinin toplamı kaçtır? A) 9 B) 12 C) 15 D) 18 E) 25 Sinüs : 1 den 1’e kadar olan değerleri alabilir. Buna göre; m 2sinx 5 ise; en küçük m 2.( : Çözüm 1) 5 7 dir. en büyük m 2.1 5 3 tür. Buna göre m tam sayı değerleri: 7, 6, 5, 4, 3 tür. Toplamları 25 buluruz. 98
www.matematikkolay.net m 3cos2x 2 olduğuna göre, m nin alabileceği kaç farklı tam sayı değeri var dır? A) 5 B) 6 C) 7 D) 8 E) 9 Kosinüs : 1 den 1’e kadar olan değerleri alabilir. Buna göre; m 3cos2x 2 ise, en küçük m : Çözüm 3.( 1) 2 1 dir. en büyük m 3.1 2 5 tir. Buna göre m tam sayı değerleri: 1,0,1,2,3,4,5 tir. 7 tane 99
2 f(x) 1 cos x olduğuna göre, f(x) fonksiyonunun görüntü kümesi aşağıdakilerden hangisidir? A) [ 1, 1] B) ( 1, 1) C) [ 1, 0] D) (0, 1] E) [0, 1] www.matematikkolay.net 2 Kosinüs, 1 ile 1 arasında değer alabilen bir fonk – siyondur. cos x ise negatif bir değer : Çözüm 2 2 alamaycağı için en az 0 olabilir. En çok da 1 olacaktır. Buna göre; en küçük f(x) 1 cos x 1 1 0 en büyük f(x) 1 cos x 1 0 1 dir. O halde f(x)’in görüntü kümesi yani alabileceği değerler : 0 ve 1 dah il, bunlar arasındaki değerler olacaktır. [0, 1] şeklinde gösterebiliriz. 109
2 sin x 1 cosx olduğuna göre, aşağıdakilerden hangisi olabi – lir? A) 1 B) 0 C) 1 D) 2 E) 3 secx www.matematikkolay.net 2 2 2 2 2 2 sin x cos x 1 olduğundan ; 1 yerine sin x cos x yazabiliriz. Buna göre; sin x 1 cosx si x s : n Çözüm 2 2 2 in x cos x cosx sin x 2 sin x 2 2 0 0 cos x cosx 0 cos x cosx 0 cosx(1 cosx) cosx 0 veya cosx 1 olmalıdır. 1 1 cosx 0 olursa secx olur. cosx 0 1 1 cosx 1 olursa secx 1 cosx 1 buluruz. 110
1 cos3x a olduğuna göre, a nın gerçel sayılarda 2 en geniş değer aralığı aşağıdakilerden hangisidi r? A) [ 1, 0] B) [2, 3] C) [3, ] D) [0, 1] E) [1, 2] www.matematikkolay.net [ 1,1] Kosinüs ve sinüs fonksiyonları [ 1,1] aralığında değer alabilir. Bu sebeple; 1 co : s3x 2 Çözüm 1 1en küçük 0 olur. 2 1 1 en büyük 1 olur. 2 O halde; [0,1] aralığında olur. 118
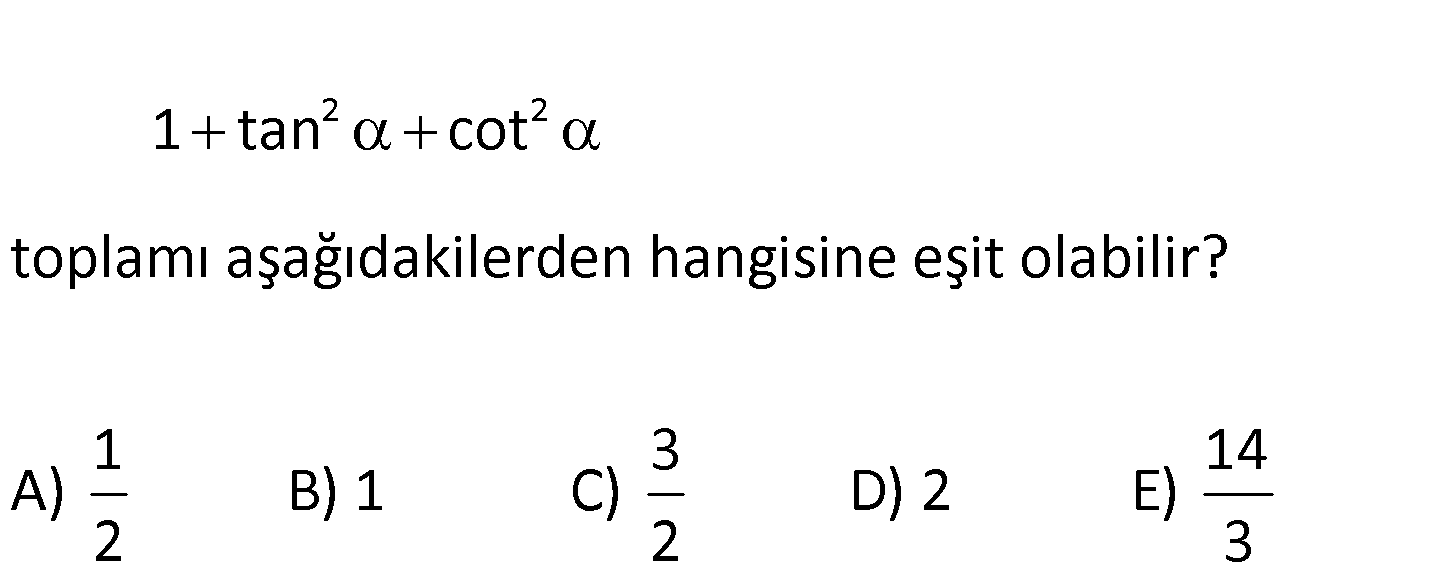
2 2 1 tan cot toplamı aşağıdakilerden hangisine eşit olabilir? 1 3 14 A) B) 1 C) D) 2 E) 2 2 3 www.matematikkolay.net 2 2 2 2 2 en az 0 olabilir tan 1 cot tan 2 cot 3 (tan cot ) 3 3′ ten büyük olmalıdır. : Çözüm E şıkkı 3′ ten büyük olduğundan Cevap : E 127
2sin(3x 5) 3a 5 eşitliğini sağlayan a tam sayılarının toplamı kaçtır? A) 5 B) 1 C) 3 D) 4 E) 6 www.matematikkolay.net 1 ile 1 arasında bir değer alabilir 2sin(3x 5) 3a 5 2sin(3x 5) 5 3a 5 3a sin(3x 5) 2 sin(3x 5) : Çözüm 5 3a 2 5 3a 1 1 2 2 5 3a 2 7 3a 3 3 3a 7 7 1 a a 1 ve 2 olabilir. 3 Toplamları 3 buluruz. 131
2 5sin 3a 7 3 olduğuna göre, a kaç farklı tamsayı değeri alabilir? A) 3 B) 4 C) 5 D) 6 E) 7 2 5sin 3a 7 3 2 3a 7 sin 3 5 sinüs, [ 1,1] aralığında değerler alır.Buna gö : re; 1 Çözüm 3a 7 1 5 5 3a 7 5 5 7 3a 5 7 2 3a 12 2 a 4 3 Buna göre bu aralıktaki tam sayıları; 1,2,3,4 4 tane buluruz. www.matematikkolay.net 133
A 10cosecx 4 A nın alamayacağı kaç tamsayı değeri vardır? A) 4 B) 12 C) 17 D) 19 E) 23 10 A 4 tür. sinx 1 sinx 1 dir. Ters çevirirsek 1 1 1 veya 1 dir. 10 il sinx si : nx Çözüm e çarpalım. 10 10 10 veya 10 dur. 4 ekleyelim. sinx sinx 10 10 4 14 veya 4 6 dır. sinx sinx Bu nedenle A 14 veya A 6 dır. 5, 4,…,13 değerlerini alamaz. 13 5 Terim Sayısı 1 18 1 19 1 buluruz. 144

