Soru Sor sayfası kullanılarak Trigonometri-1 konusu altında Büyük açıların trigonometrik oranları, Geniş açıların trigonometrik oranları, Trigonometrik indirgeme ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
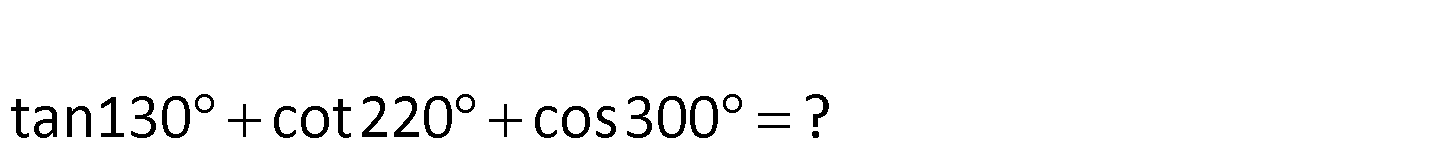
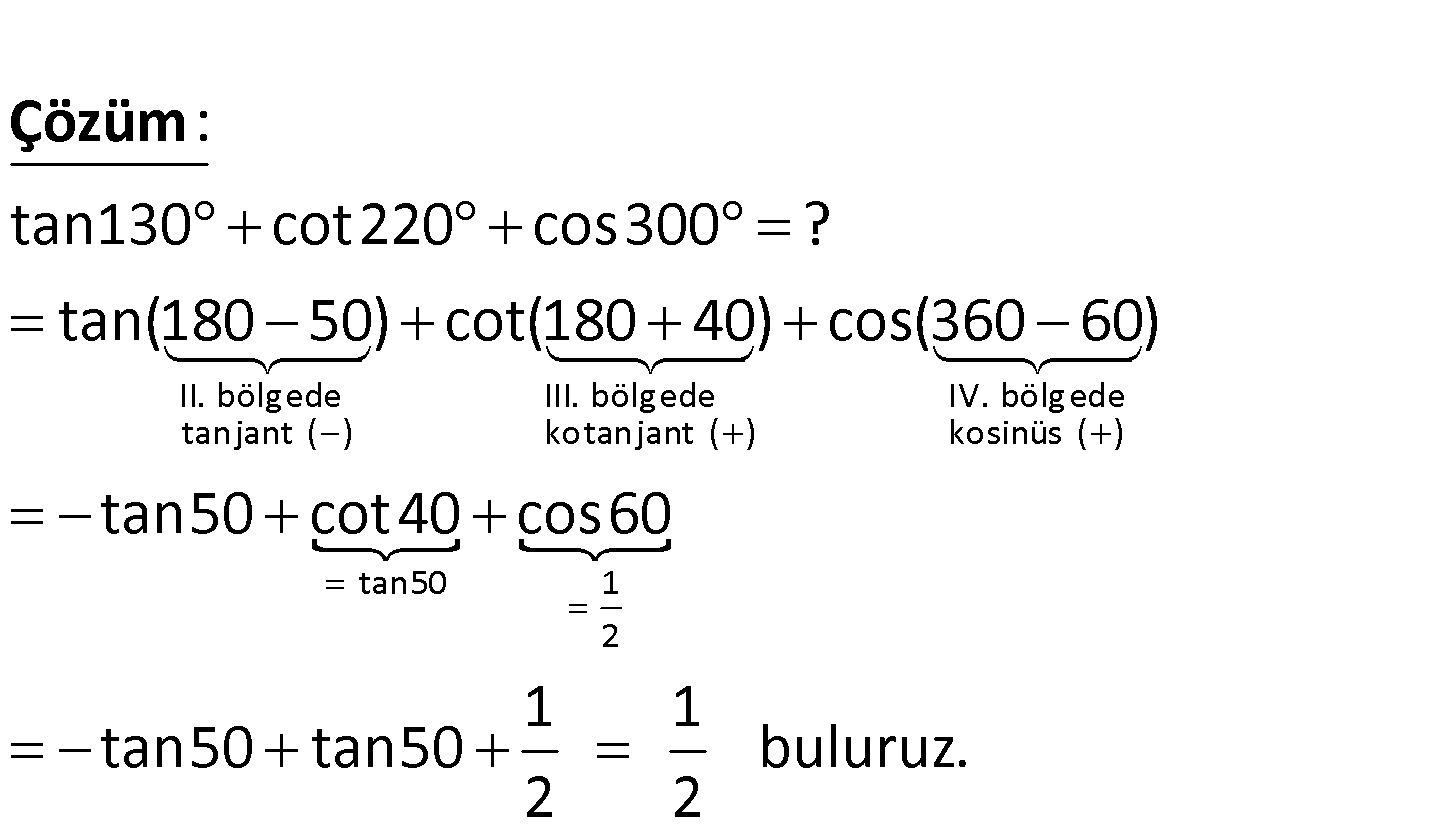
2.SORU

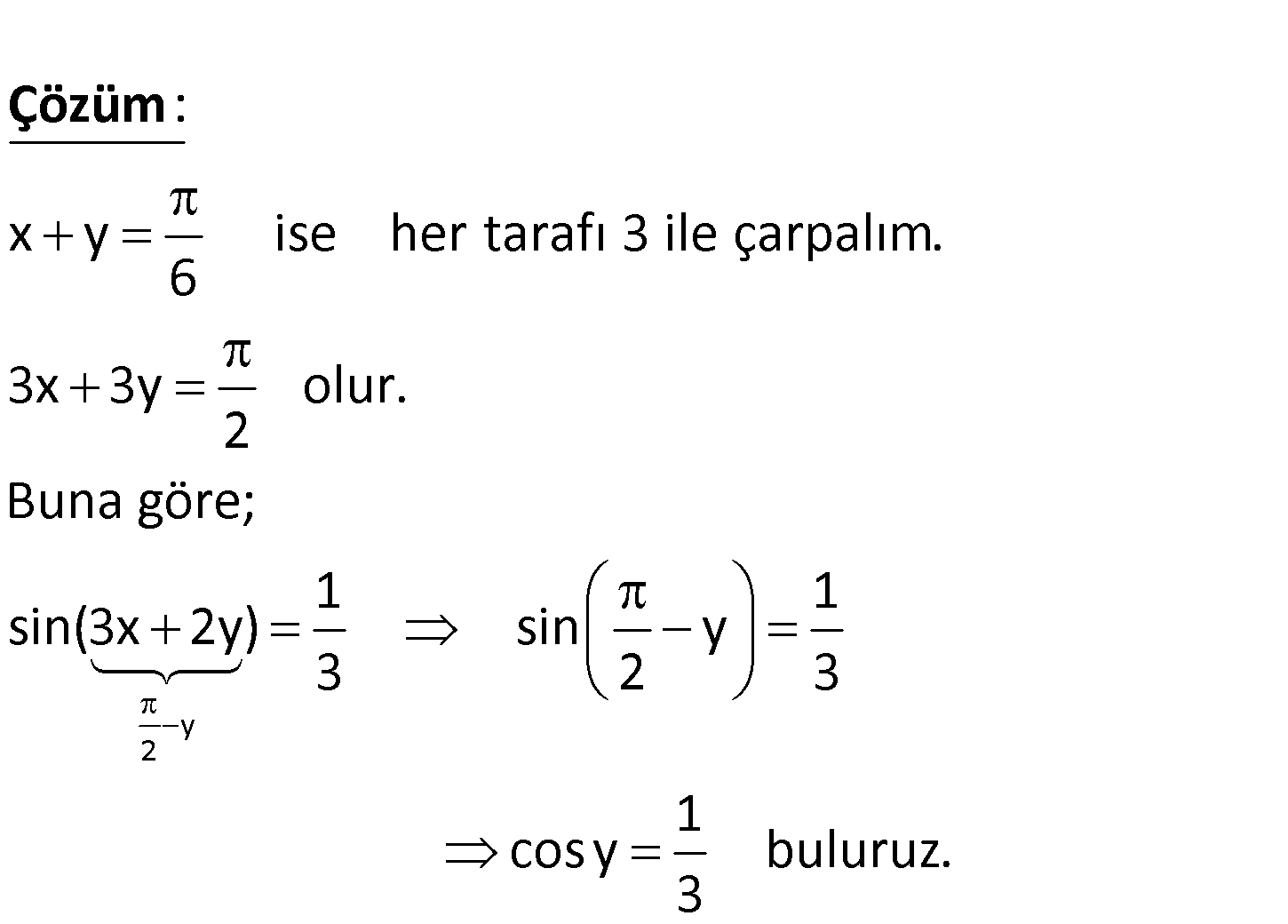
3.SORU
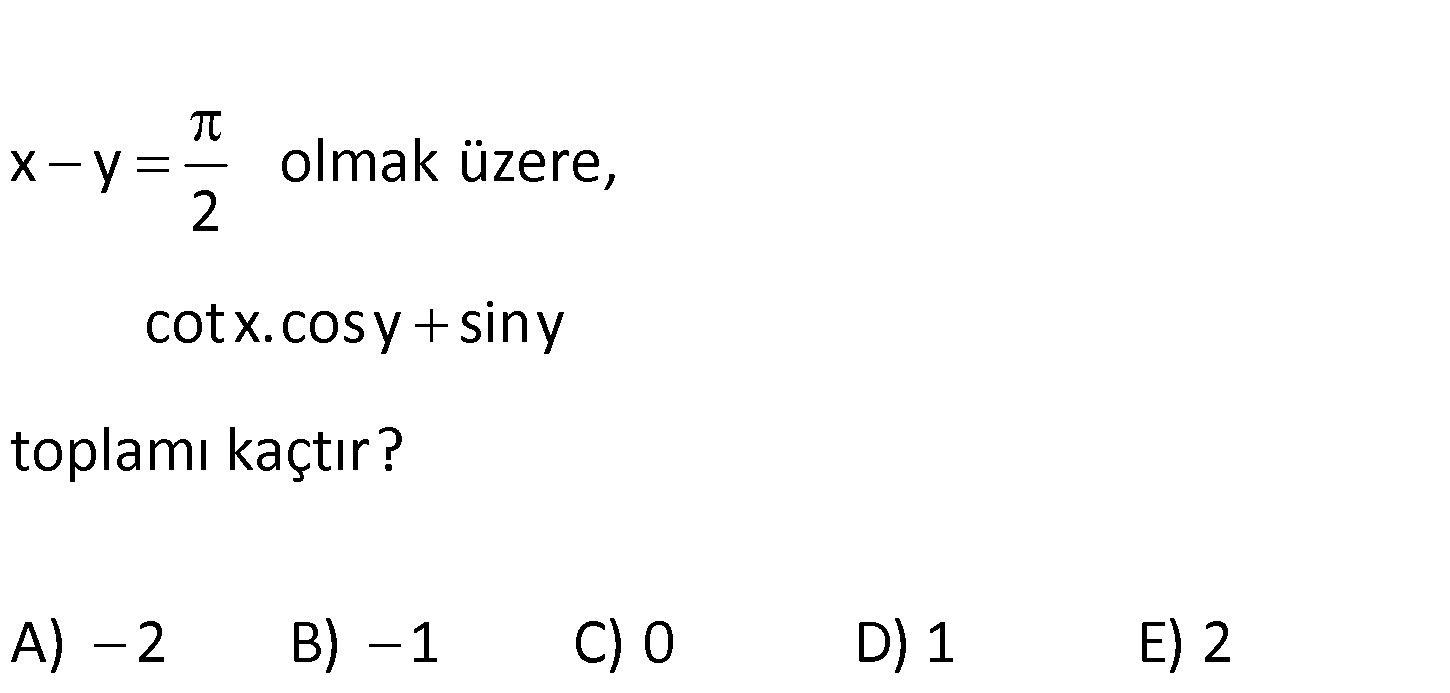
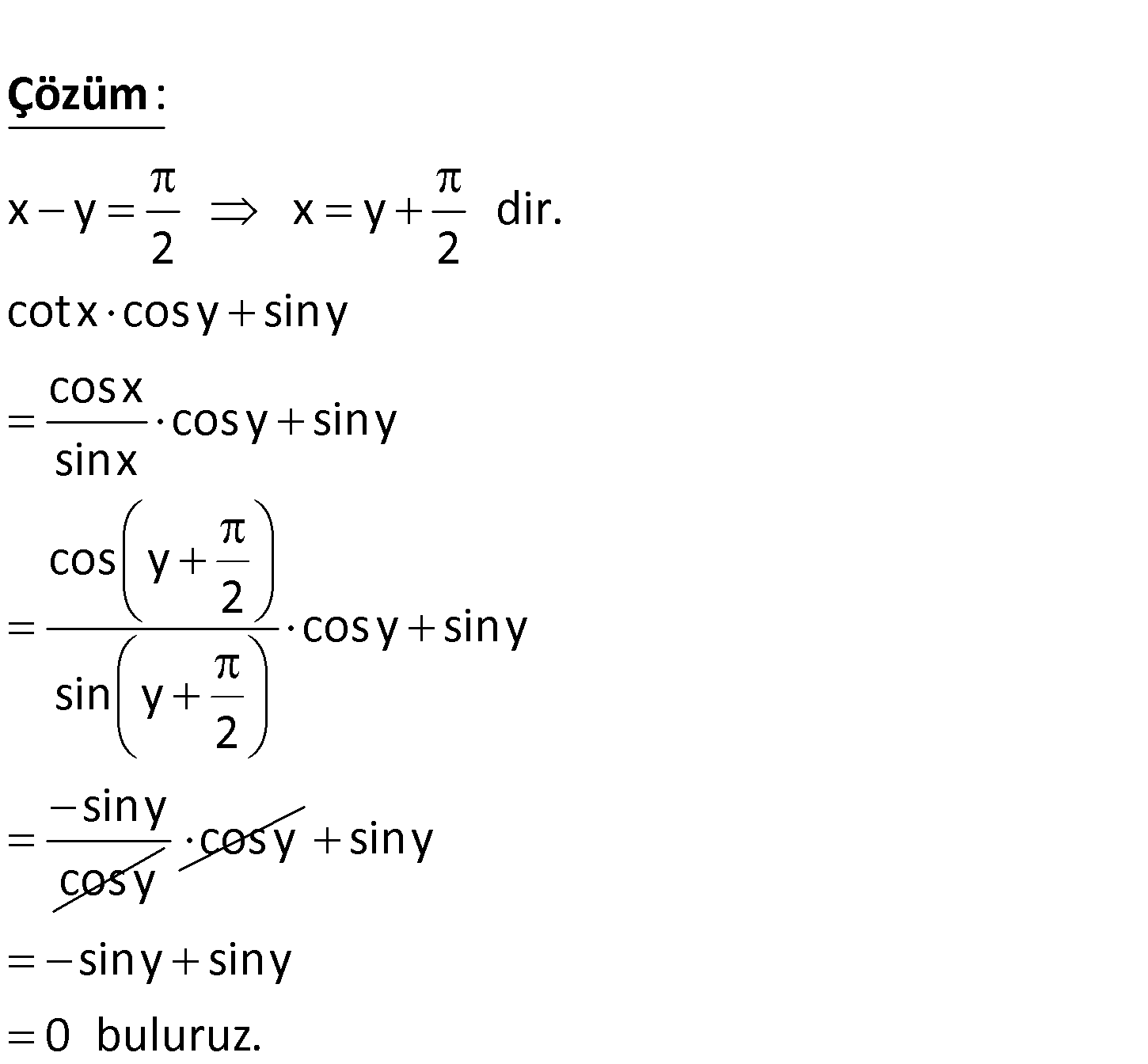
4.SORU

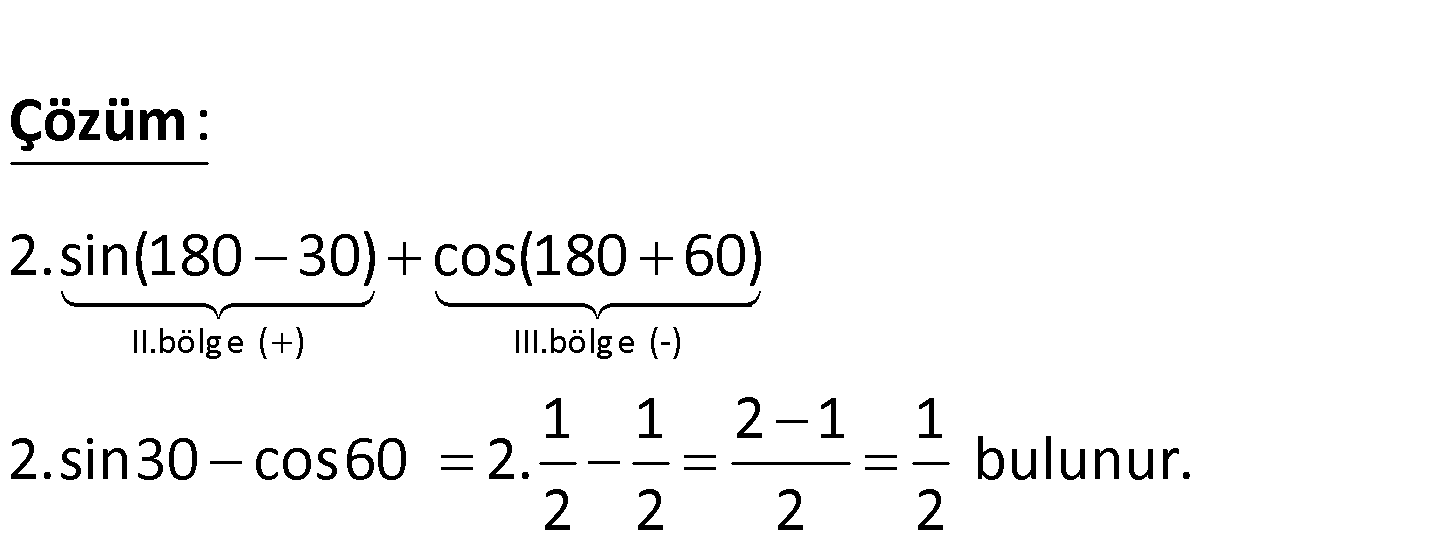
5.SORU

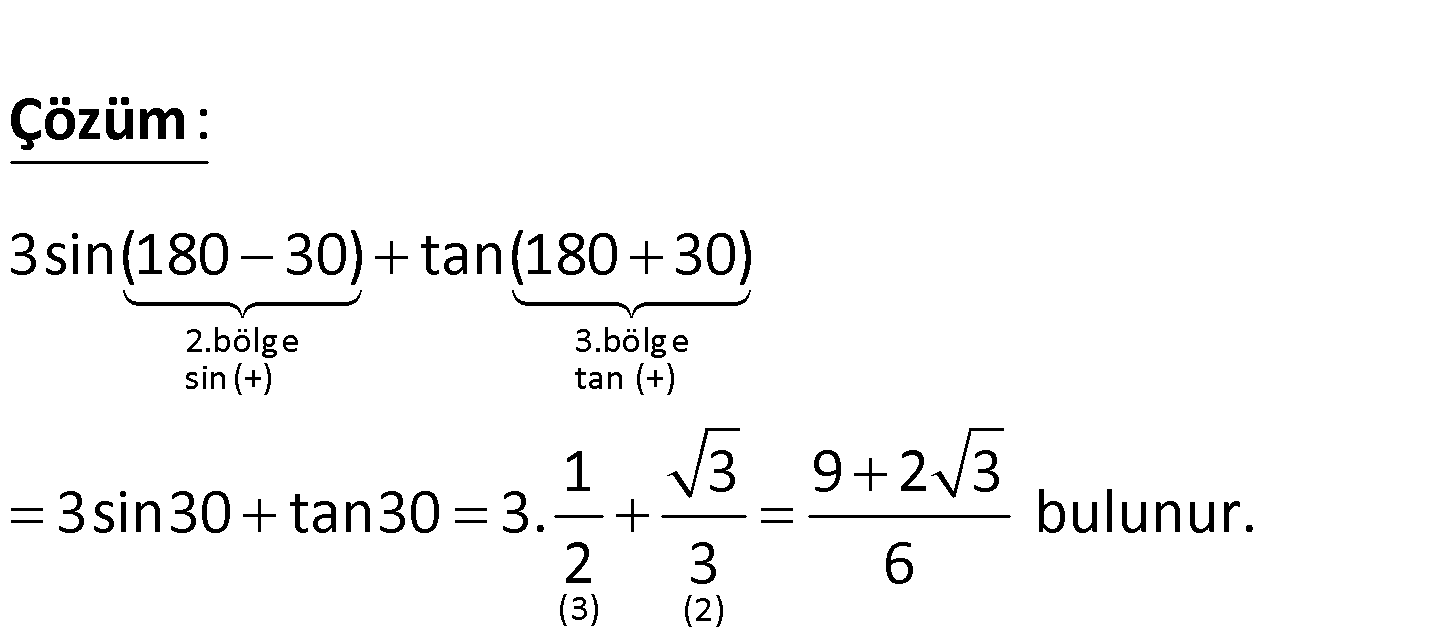
6.SORU

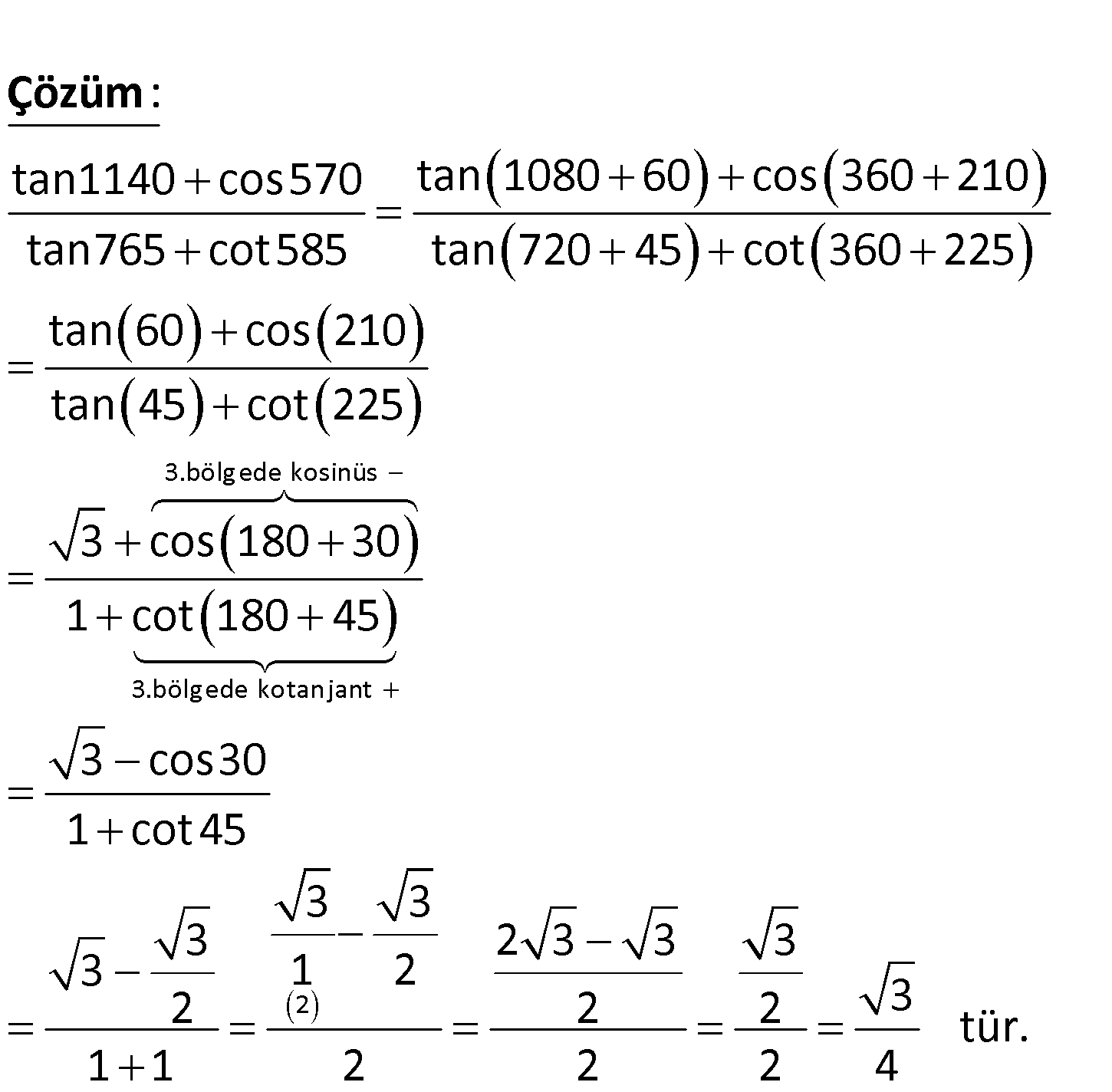
7.SORU
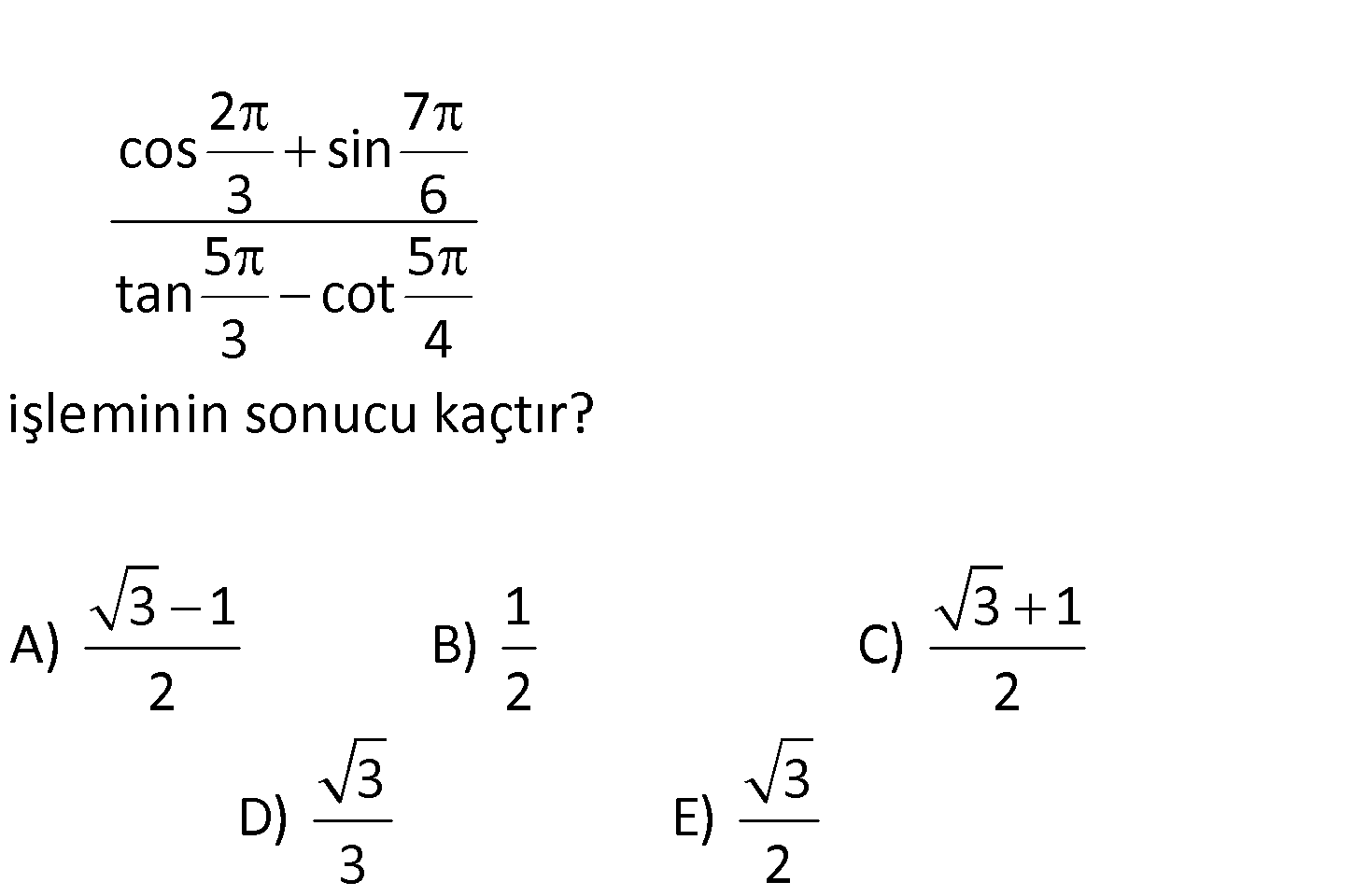
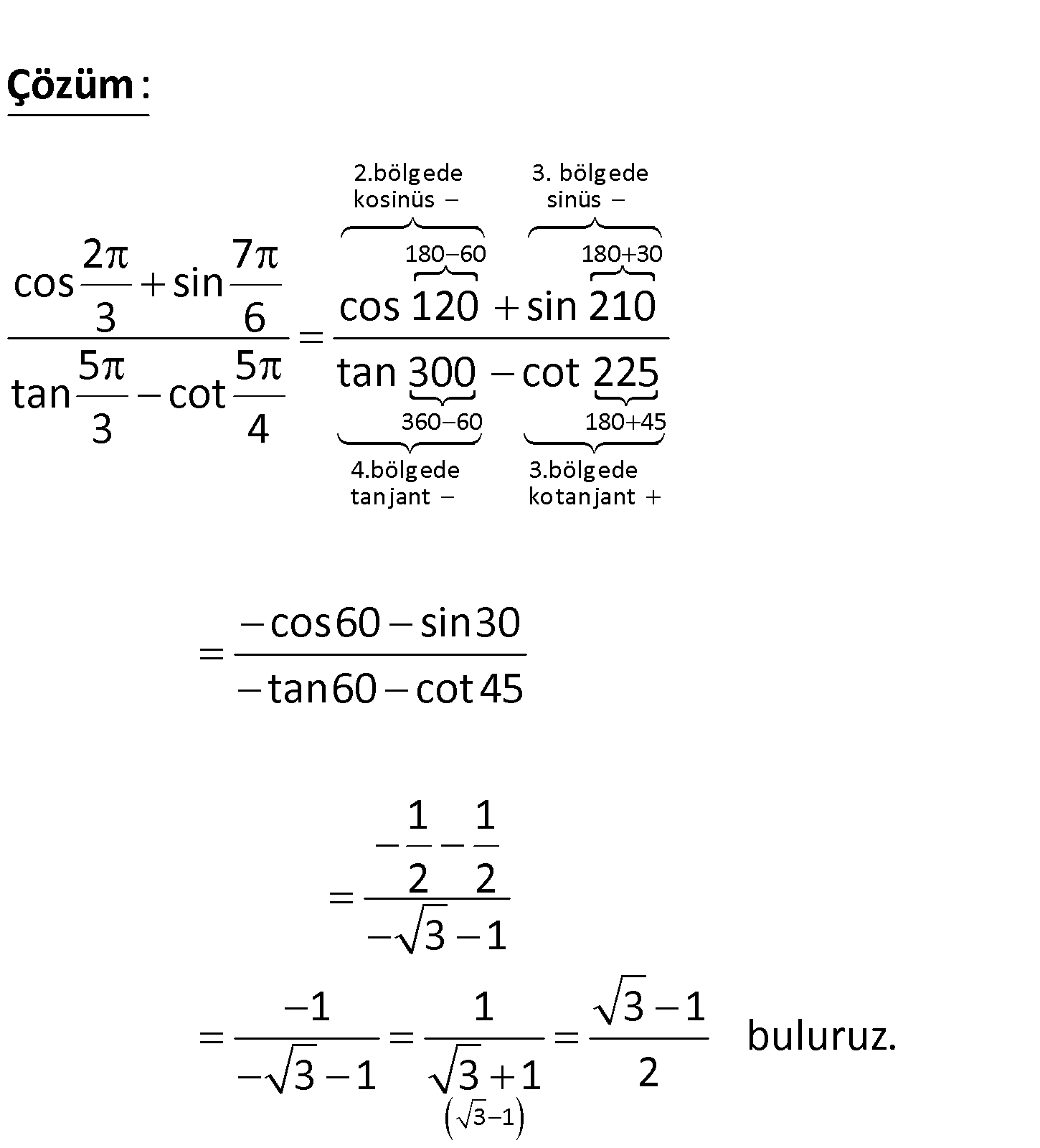
8.SORU

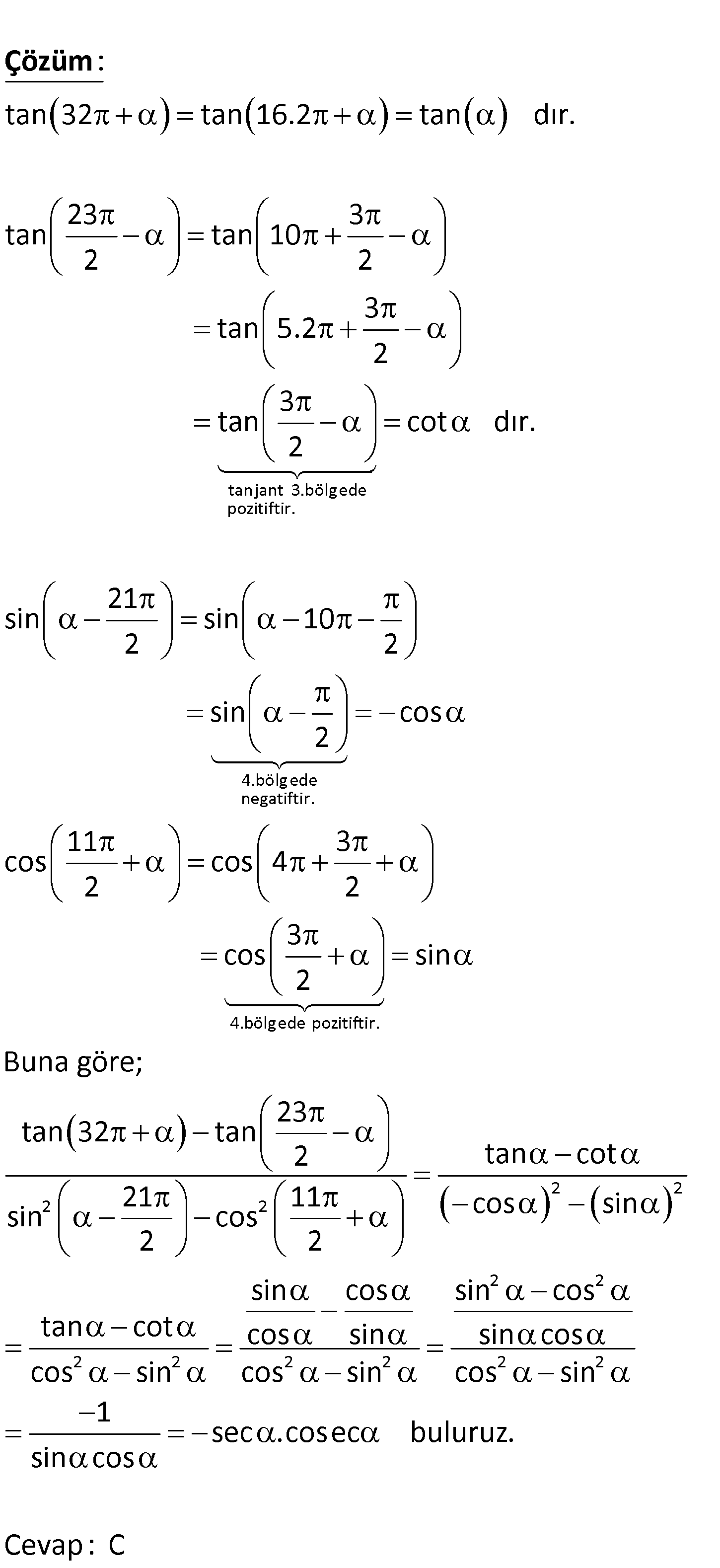
9.SORU

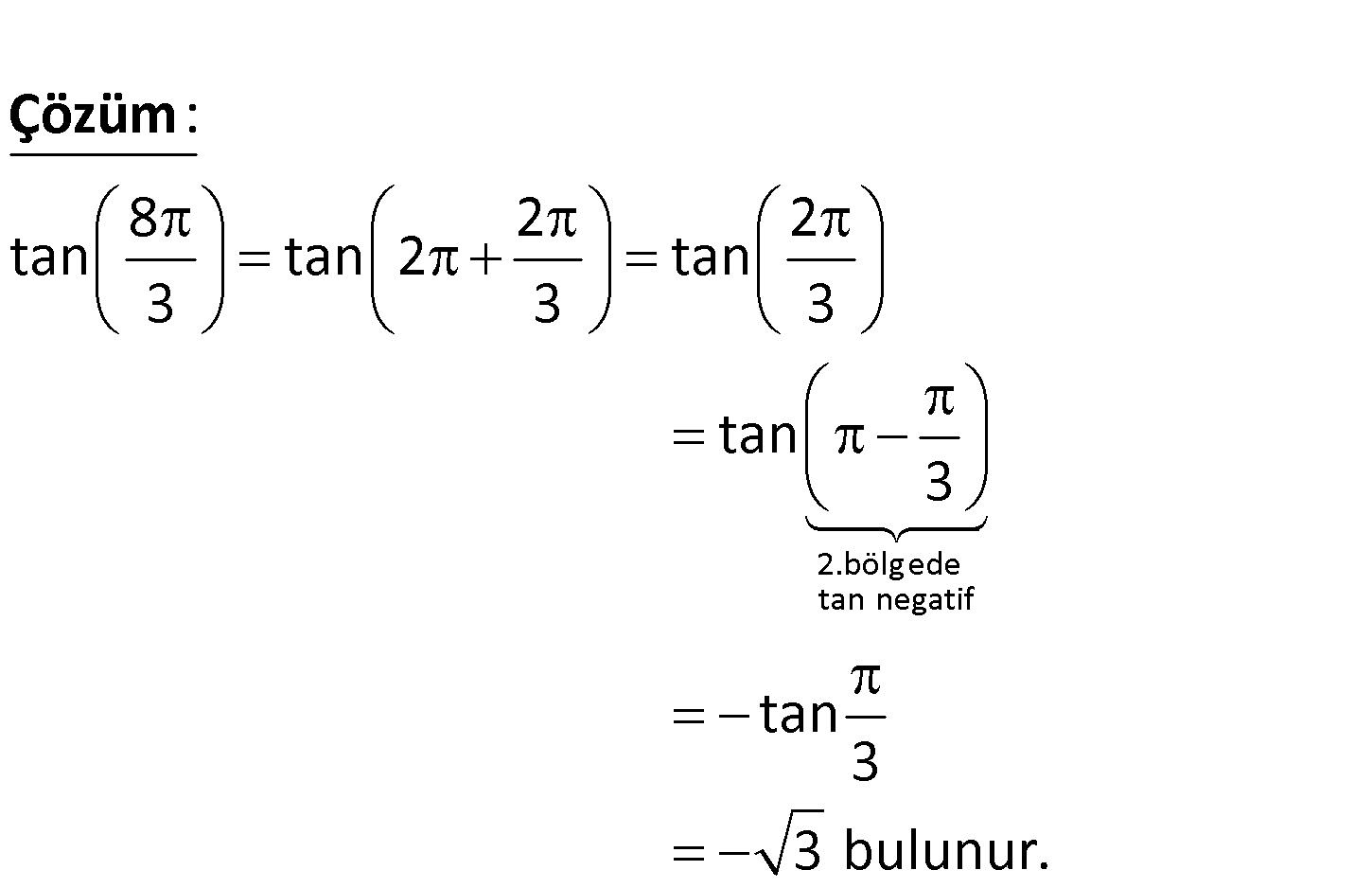
10.SORU
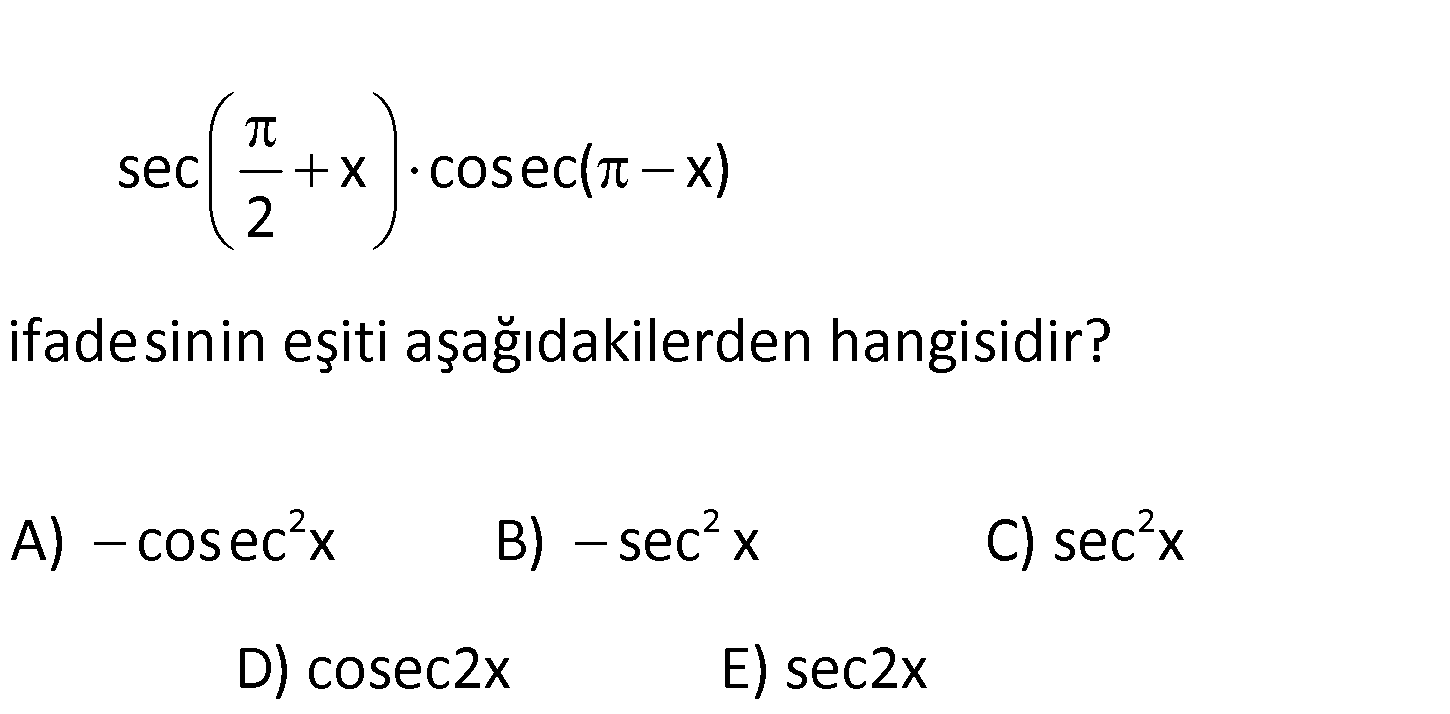
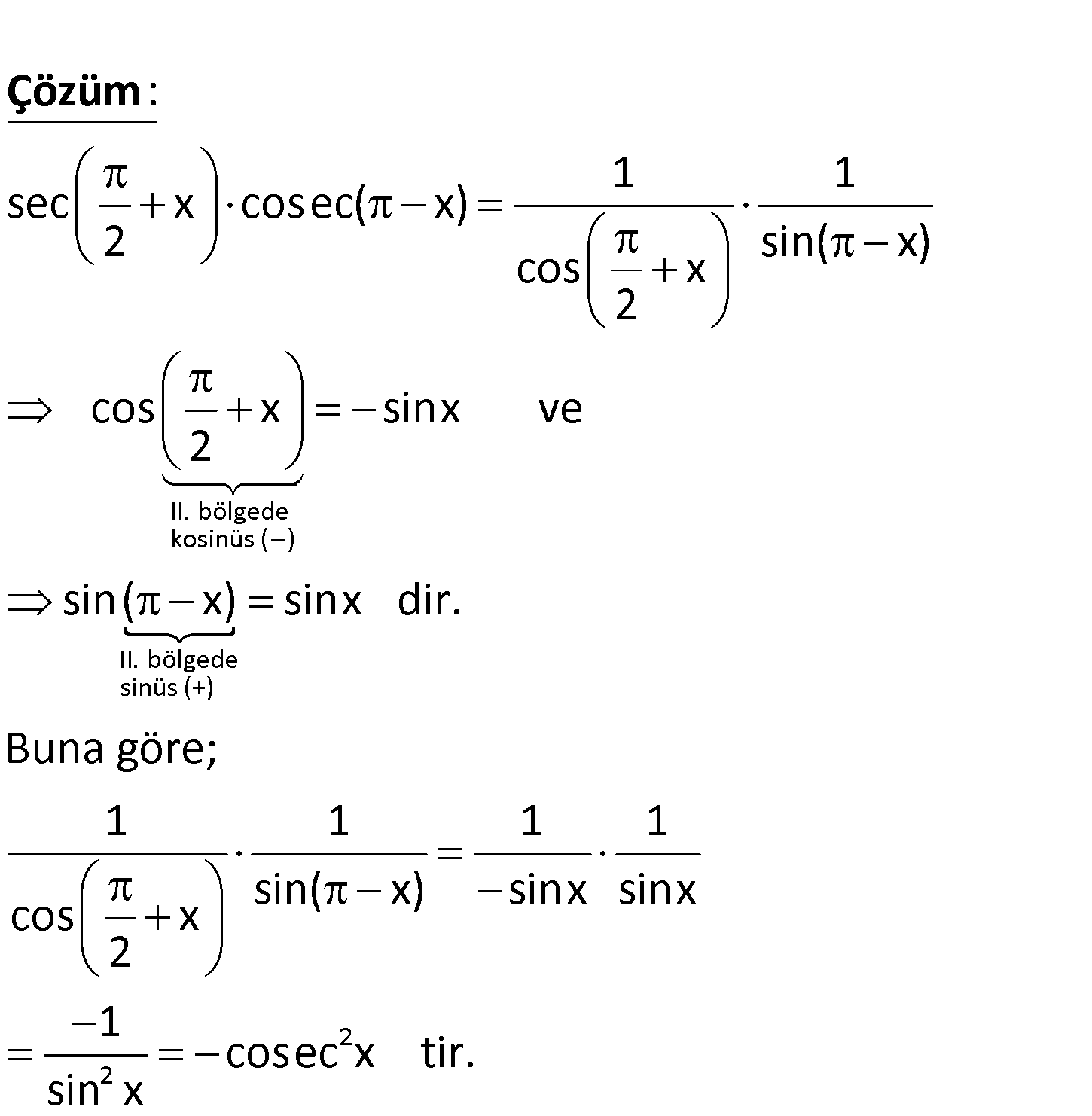
11.SORU
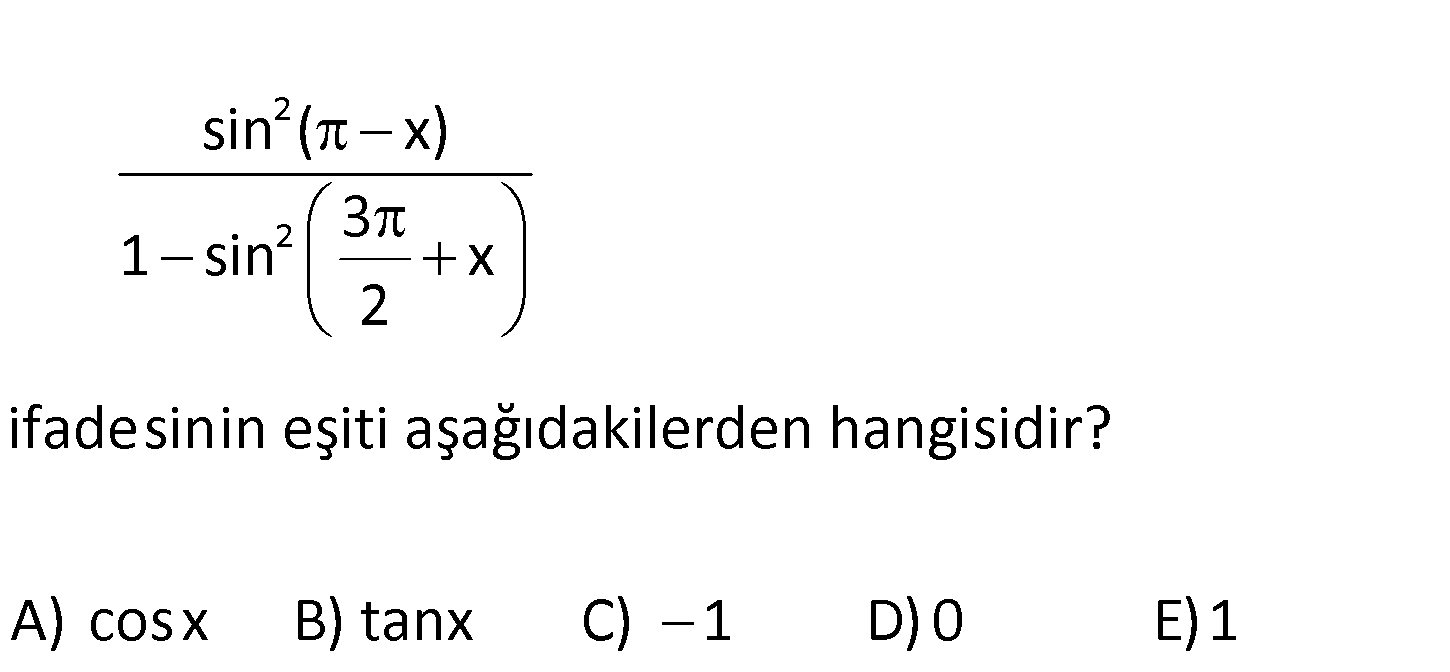
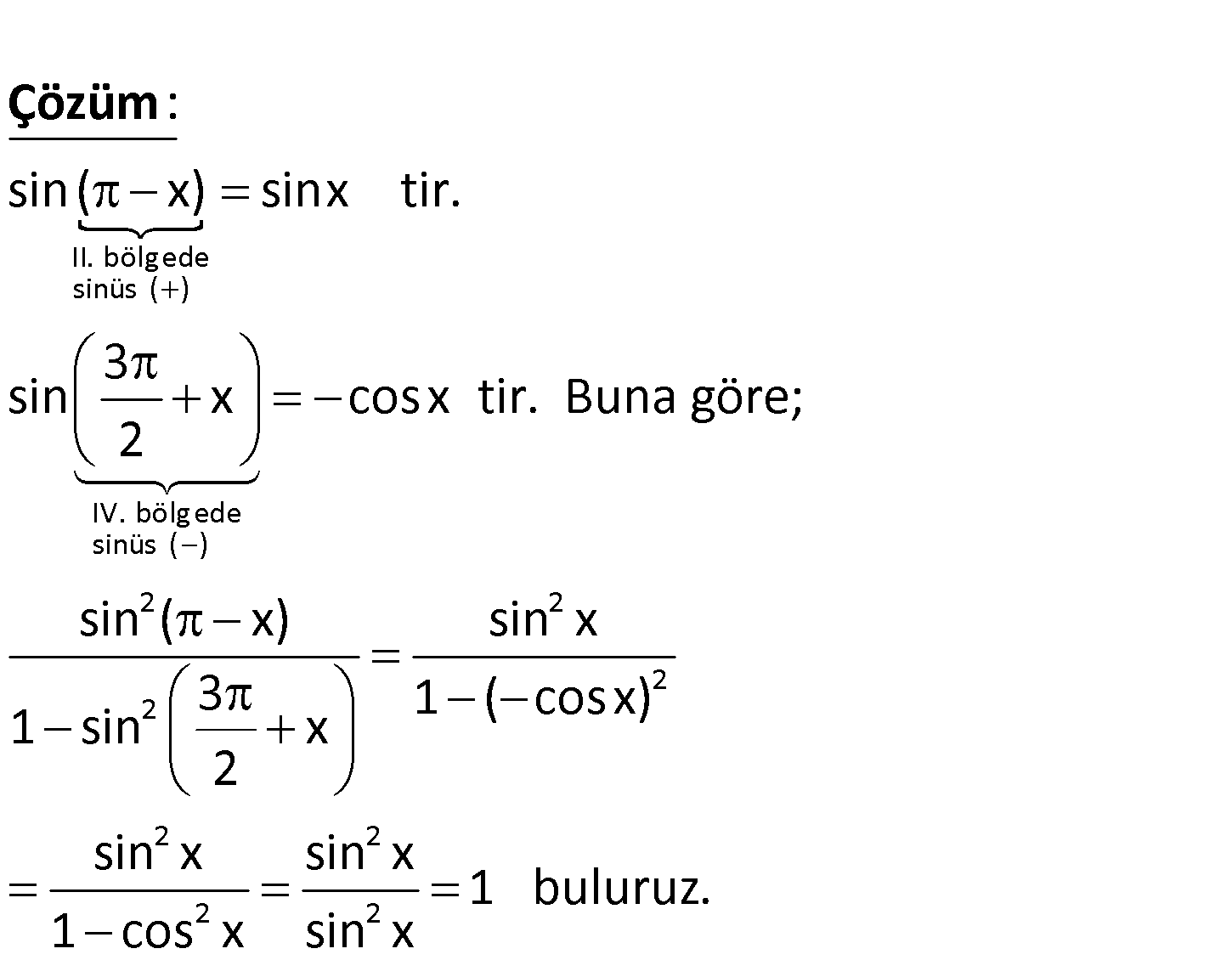
12.SORU
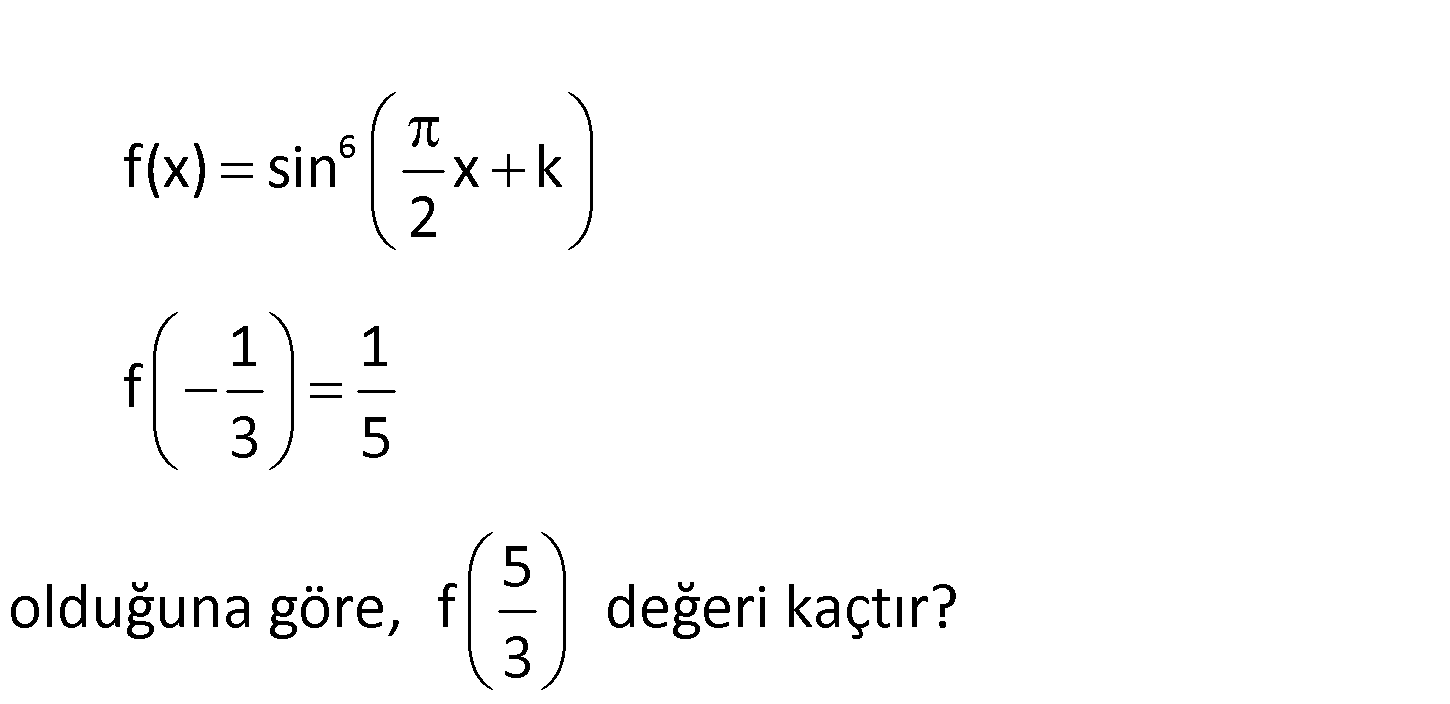
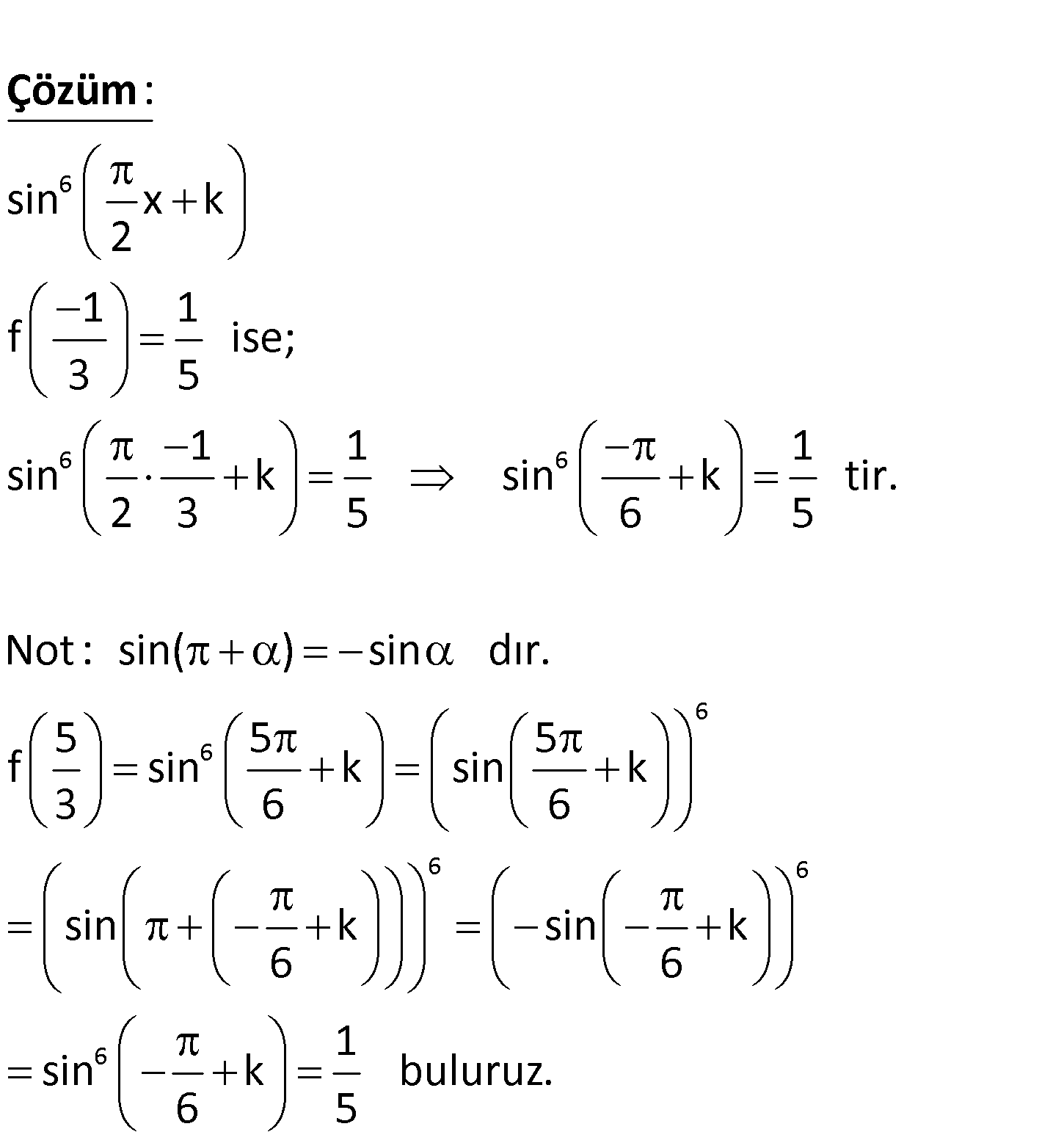
13.SORU


14.SORU
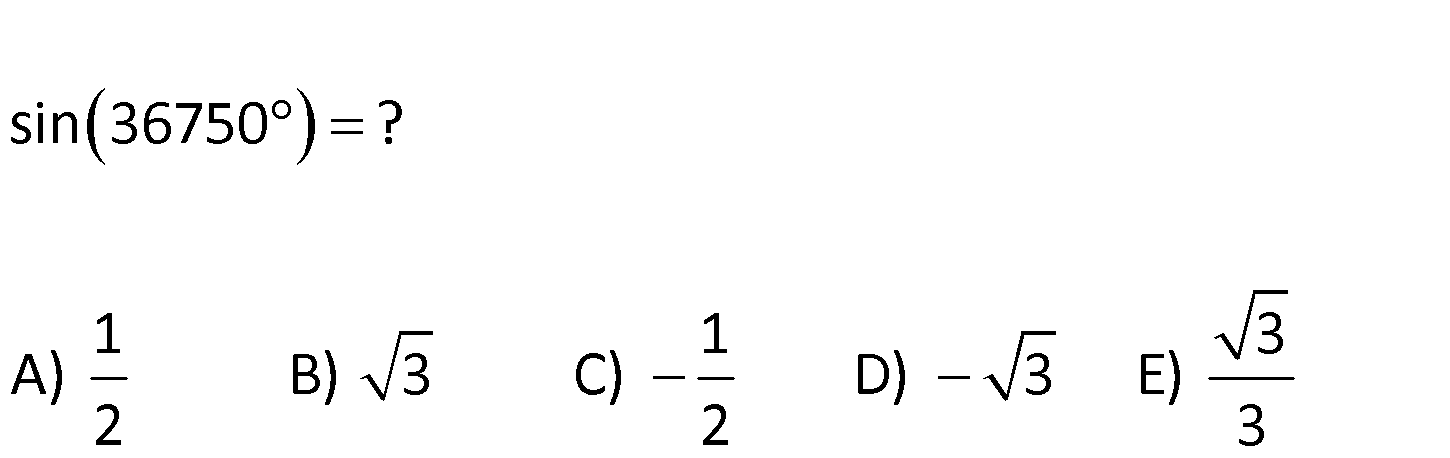
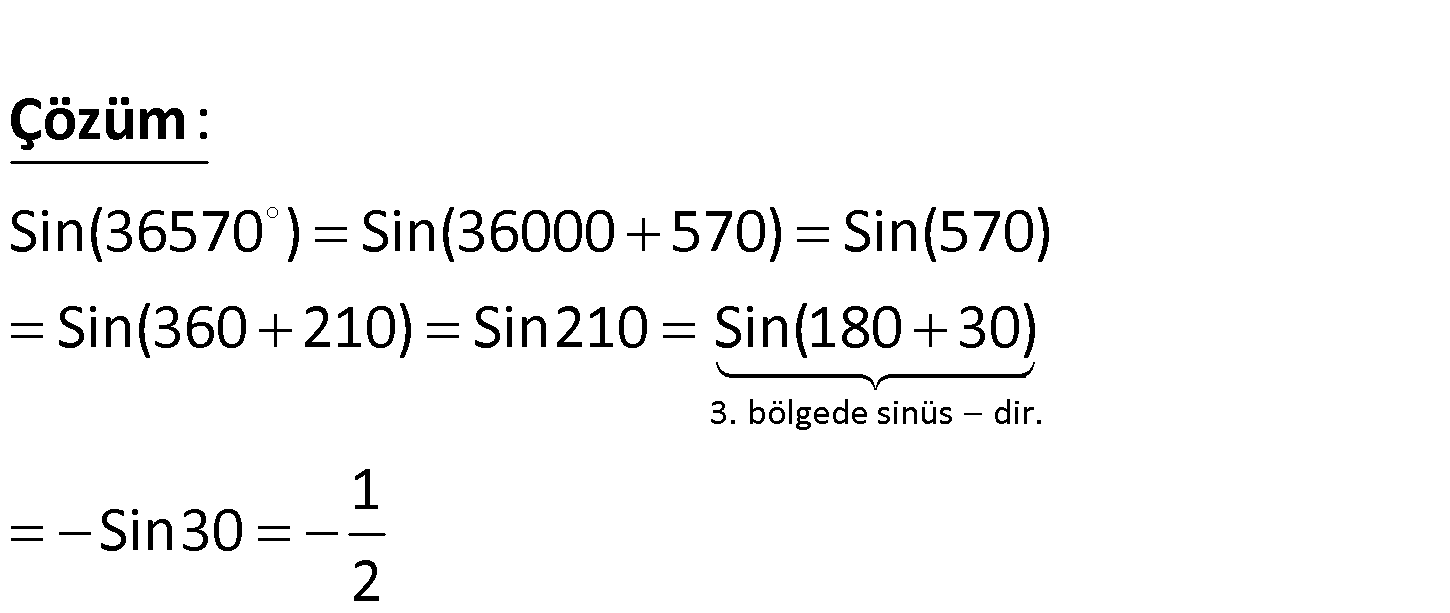
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
tan130cot220cos300 ? II. bölgede III. bölgede tanjant ( ) kota tan130 cot220 cos300 ? tan(180 50) cot(180 : 40 Çözüm IV. bölgede njant ( ) kosinüs ( ) tan50 1 2 ) cos(360 60) tan50 cot40 cos60 1 1 tan50 tan50 buluruz. 2 2 16
x y olmak üzere, 6 1 sin 3x 2y 3 olduğuna göre, cos y değeri kaçtır? 1 3 1 1 A) B) C) D) E) 2 3 3 2 3 1 6 www.matematikkolay.net y 2 x y ise her tarafı 3 ile çarpalım. 6 3x 3y olur. 2 Buna göre; 1 sin(3x 2y) : 3 Çözüm 1 sin y 2 3 1 cos y buluruz. 3 3
x y olmak üzere, 2 cotx.cos y siny toplamı kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 www.matematikkolay.net x y x y dir. 2 2 cotx cos y siny cosx cos y siny sinx cos y 2 cos y siny sin y 2 : Çözüm siny cos y cos y siny siny siny 0 buluruz. 5
2sin1 50 ? cos240 II.bölge ( ) III.bölge (-) : 2.sin(180 30) cos(180 60) 1 1 2 1 2.si n30 cos60 2. 2 2 2 Çözüm 1 bulunur. 2 22
3 sin150 tan 2 10 ? 2.bölge 3.bölge sin (+) tan (+) (3) (2) : 3sin(180 30) tan(180 30) 1 3 9 3sin30 tan30 3. 2 3 Çözüm 2 3 bulunur. 6 25
www.matematikkolay.net tan1140 cos570 ifadesinin değerini bulunuz. tan765 cot585 tan1140 cos570 tan 1080 60 cos 360 210 tan765 cot585 tan 720 45 cot 360 225 tan 60 cos 210 tan 45 cot : 2 Çözüm 3.bölgede kosinüs 3.bölgede kotanjant 2 25 3 cos 180 30 1 cot 180 45 3 cos30 1 cot45 3 3 3 2 3 3 3 3 1 2 2 2 2 3 tür. 1 1 2 2 2 4 45
2 7 cos sin 3 6 5 5 tan cot 3 4 işleminin sonucu kaçtır? 3 1 1 3 1 A) B) C) 2 2 2 3 3 D) E) 3 2 www.matematikkolay.net 2.bölgede 3. bölgede kosinüs sin 180 60 180 30 2 7 cos sin 3 6 cos 120 sin 210 5 5 tan cot 3 4 : Çözüm üs 360 60 180 45 4.bölgede 3.bölgede tanjant kotanjant 3 tan 300 cot 225 cos60 sin30 tan60 cot45 1 1 2 2 3 1 1 1 3 1 3 1 13 1 buluruz. 2 47
2 2 23 tan 32 tan 2 21 11 sin cos 2 2 ifadesinin eşiti aşağıdakilerden hangisidir? A) sec .cos B) cosec .sec C) sec .cosec D) tan E) sin .cosec www.matematikkolay.net tan 32 tan 16.2 tan dır. 23 3 tan tan 10 2 2 : Çözüm tanjant 3.bölgede pozitiftir. 4.bölgede negatiftir. 3 tan 5.2 2 3 tan cot dır. 2 21 sin sin 10 2 2 sin 2 4.bölgede pozitiftir. 2 2 cos 11 3 cos cos 4 2 2 3 cos sin 2 Buna göre; 23 tan 32 tan 2 tan cot 21 11 cos sin cos 2 2 2 2 2 2 2 2 2 2 2 2 sin sin cos sin cos tan cot cos sin sin cos cos sin cos sin cos sin 1 sec .cosec buluruz. sin cos Cevap: C www.matematikkolay.net 70
www.matematikkolay.net 8 tan ? 3 8 2 2 tan tan 2 tan 3 3 3 : t Çözüm 2.bölgede tan negatif an 3 tan 3 3 bulunur. 72
www.matematikkolay.net 2 2 sec x cosec( x) 2 ifadesinin eşiti aşağıdakilerden hangisidir? A) cosec x B) sec x C) 2 sec x D) cosec2x E) sec2x II. bölgede kosinüs ( ) 1 1 sec x cosec( x) 2 sin( x) cos x 2 cos x 2 : Çözüm II. bölgede sinüs (+) 2 2 sinx ve sin( x) sinx dir. Buna göre; 1 1 1 1 sin( x) sinx sinx cos x 2 1 cosec x tir. sin x 100
www.matematikkolay.net 2 2 sin ( x) 3 1 sin x 2 ifadesinin eşiti aşağıdakilerden hangisidir? A) cosx B) tanx C) 1 D) 0 E)1 II. bölgede sinüs ( ) IV. bölgede sinüs ( ) sin( x) sinx tir. 3 sin x cosx t . : ir 2 Çözüm 2 2 2 2 2 2 2 2 Buna göre; sin ( x) sin x 3 1 ( cosx) 1 sin x 2 sin x sin x 1 buluruz. 1 cos x sin x 102
6 f(x) sin x k 2 1 1 f 3 5 5 olduğuna göre, f değeri kaçtır? 3 6 6 6 sin x k 2 1 1 f ise; 3 5 1 1 1 sin k sin k tir. 2 3 : 5 6 5 Not : s Çözüm 6 6 6 6 6 in( ) sin dır. 5 5 5 f sin k sin k 3 6 6 sin k sin k 6 6 1 sin k buluruz. 6 5 www.matematikkolay.net 136
www.matematikkolay.net tan20 m olmak üzere, tan160 cot110 tan200 cot340 ifadesinin m cinsinden eşiti aşağıd 2 2 3 2 3 2 3 akilerden hangisidir? m 1 m 2m A) B) C) 1 m m 1 m m m D) E) 1 m 1 2m 2.bölgede tanjant dir. 2.bölgede kotanjant tan 160 tan 180 20 tan20 dir. cot110 cot 90 20 : Çözüm dir. 3.bölgede tanjant dır. 4.bölgede kotanjant dir. tan20 dir. tan200 tan 180 20 tan20 dir. cot340 cot 360 20 cot20 dir. Buna göre; tan160 cot110 tan20 tan20 tan200 cot340 tan20 cot 2 2 2 2 2 20 1 Not : tan20 m ise cot20 dir. m Buna göre; m m 2m 2m 2m dir. 1 m m 1 m 1 1 m m m www.matematikkolay.net 143
sin 36750 ? 1 1 3 A) B) 3 C) D) 3 E) 2 2 3 3. bölgede sinüs dir. Sin(36570 ) Sin(36000 570) Sin(570) Sin(360 210) Sin210 : Sin(180 30) Çözüm 1 Sin30 2 2

