Soru Sor sayfası kullanılarak Polinomlar konusu altında Polinomun 2.derece bir ifadeye bölünmesi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

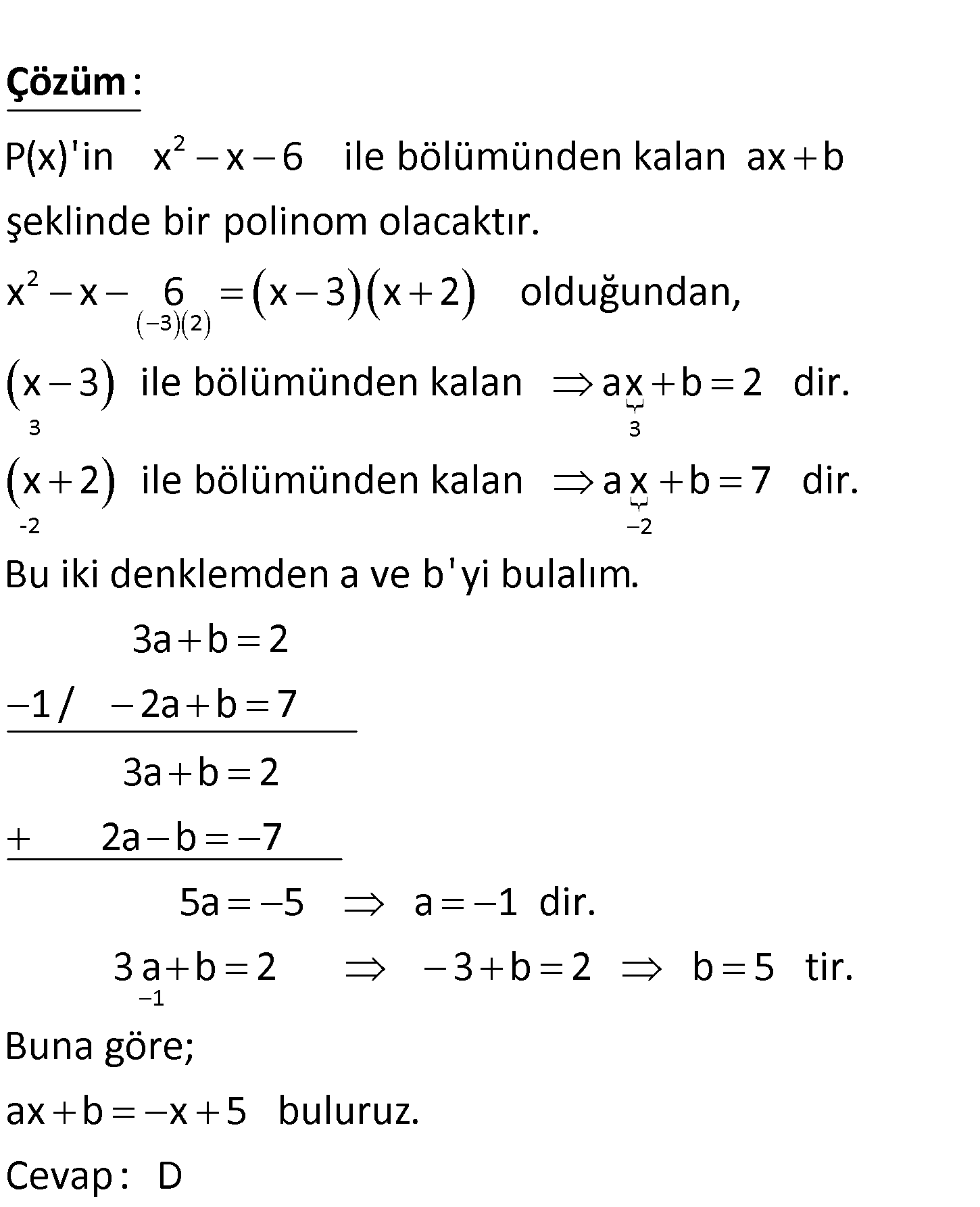
2.SORU


3.SORU


4.SORU


5.SORU


6.SORU


7.SORU

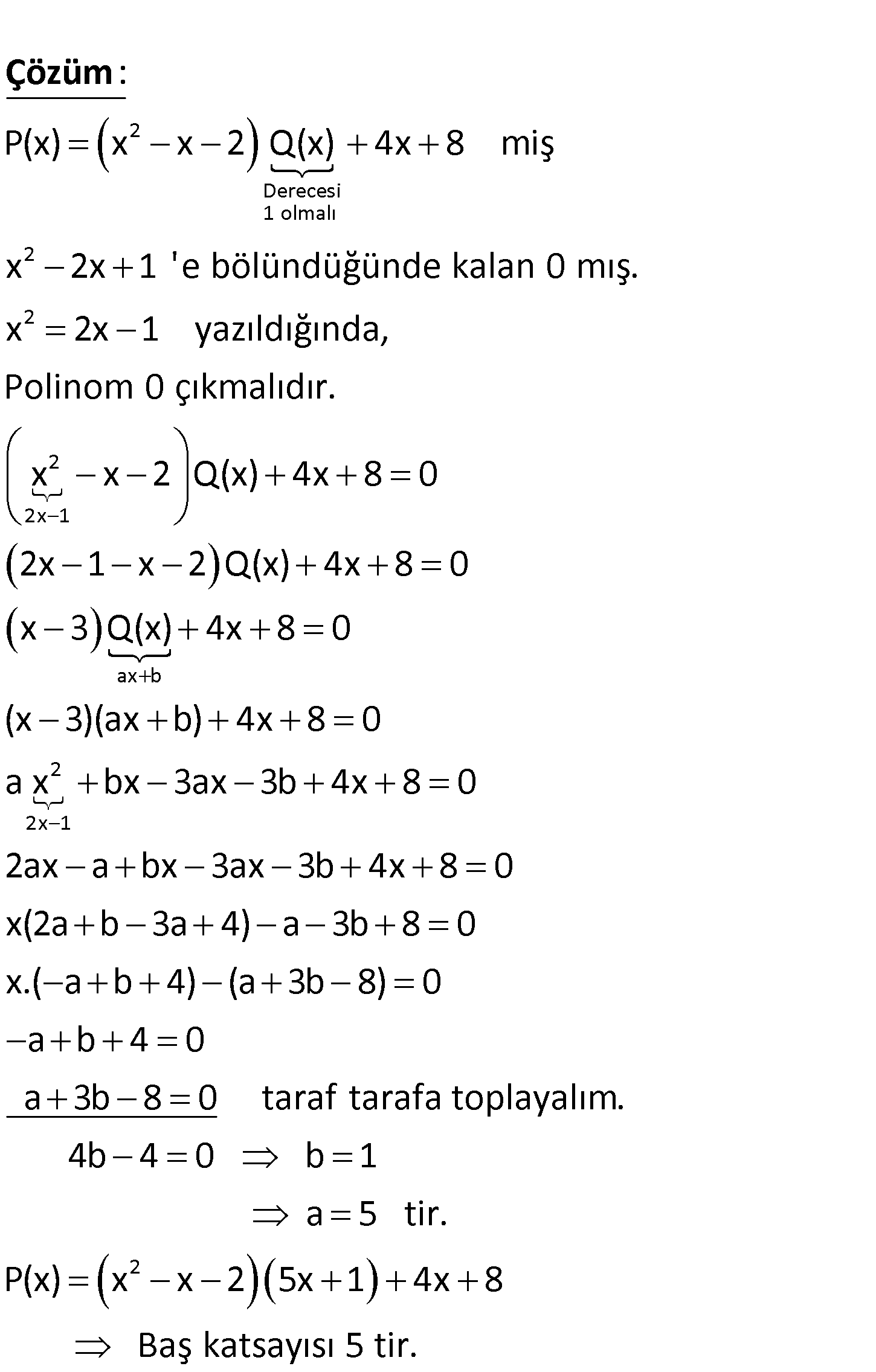
8.SORU


9.SORU


10.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
P x polinomunun x 3 ile bölünmesinden elde edilen kalan 2, x 2 ile bölünmesinden elde edi – len kalan 2 7 dir. Buna göre, P x polinomunun x x 6 ile bö – lünmesinden kalan aşağıdakilerden hangisidir? A) 2x 5 B) x 1 C) 3x 1 D) 5 x E) 2x 2 www.matematikkolay.net 2 2 3 2 P(x)’in x x 6 ile bölümünden kalan ax b şeklinde bir polinom olacaktır. x x 6 3 : x Çözüm 3 3 -2 2 x 2 olduğundan, x 3 ile bölümünden kalan ax b 2 dir. x 2 ile bölümünden kalan a x b 7 dir. Bu iki denklemden a ve b’ yi bulalım. 3a b 2 1 / 2a b 7 1 3a b 2 2a b 7 5a 5 a 1 dir. 3 a b 2 3 b 2 b 5 tir. Buna göre; ax b x 5 buluruz. Cevap: D 50
2 2 P x polinomunun x 3x 4 ile bölünmesinden kalan 2x 5, x 4x 5 ile bölünmesinden kalan 3x 4 tür. Buna 2 göre, P x polinomunun x 9x 20 ile bö – lünmesinden kalan aşağıdakilerden hangisidir? A) 3x 5 B) 7x 4 C) 6x 11 D) 6x 17 E) 8x 11 www.matematikkolay.net 2 4 2 x 3x 4 x 4 x 1 dir. x 4 ile bölümünden kalanı bulmak için x 4 yazarız. P(4) 2x 5 13 tür. x : Çözüm 5 2 2 4x 5 x 5 x 1 dir. x 5 ile bölümünden kalanı bulmak için x 5 yazarız. P(5) 3x 4 19 dur. P(x)’in x 9x 20 ile bölümünden kalan ax b şeklinde bir polinomdur. x 9x 20 x 4 x 5 olduğundan; x 4 ile bölümü 4 5 nden kalan ax b 13 4a b 13 x 5 ile bölümünden kalan ax b 19 5a b 19 Bu iki denklemi çözelim. 4a b 6 13 5a b 19 taraf tarafa çıkaralım. a 6 a 6 dır. 4a b 13 24 b 13 b 11 dir. Buna göre; ax b 6x 11 buluruz. 53
2 P x polinomunun katsayılar toplamı 6, sabit terimi 0 dır. Buna göre, P x polinomunun x x ile bölünme – sinden kalan aşağıdakilerden hangisidir? A) 6x B) 6x 1 C) 2x 2 D) 2x E) 2 www.matematikkolay.net 2 2 P(x)’in x x ile bölümünden kalan ax b şeklinde bir polinom olacaktır. x x x x 1 l : o Çözüm 0 1 duğundan, Sabit terim: x 0 yazılarak bulunur. ax b 0 ise b 0 dır. Katsayılar toplamı: x 1 yazılarak bulunur. ax 0 6 ise a 6 dır. Buna göre; ax b 6x 0 6x buluruz. Cevap: A 51
www.matematikkolay.net 2 Bir P x polinomunun x 2 ile bölünmesinden elde edilen kalan a, x x 2 ile bölünmesinden elde edilen kalan ax 9 olduğuna göre, a kaçtır? A) 5 B) 4 C) 3 D) 1 E) 5 2 2 P 2 a dır. x x 2 x 2 x 1 dir. x x 2 ile bölümünden kalan ax 9 ise, x 2 için P 2 a x : Çözüm 2 9 eşit olmalıdır. a 2a 9 3a 9 a 3 buluruz. 56
www.matematikkolay.net 3 2 3 2 Bir P x polinomu x 1 ile bölündüğünde 2x x 1 kalanını, x 1 ile bölündüğünde x 3 kalanını veriyor 2 . Buna göre, P x polinomu x 1 ile bölündüğün – de kalan aşağıdakilerden hangisidir? A) 2x 1 B) 3x 1 C) x 2 D) 2x 3 E) 3x 2 www.matematikkolay.net 3 2 3 2 x 1 ile bölündüğünde 2x x 1 kalıyorsa P(x) x 1 A(x) 2x x 1 şeklinde yazılabilir. x 1 ç : i Çözüm 3 2 0 3 2 3 2 3 2 0 2 in; P(1) x 1 A(x) 2x x 1 2 1 1 4 tür. x 1 ile bölündüğünde x 3 kalıyorsa P(x) x 1 B(x) x 3 şeklinde yazılabilir. x 1 için; P( 1) x 1 B(x) x 3 1 3 2 dir. P(x)’in x 1 ile bölümünd 2 2 0 2 0 en kalan ax b şeklindedir. P(x) x 1 C x ax b şeklinde yazılabilir. x 1 için; P(1) x 1 C x ax b 4 a b dir. x 1 için; P( 1) x 1 C x ax b 2 a b dir. 1 toplayınca 2 2b b 1 dir. 4 a b a 3 tür. O halde kalan ax b 3x 1 dir. 68
www.matematikkolay.net P x polinomu x 3 ile bölündüğünde bölüm Q x , kalan 1 dir. Q x polinomu x 1 ile bölündüğün – de kalan 2 2 dir. Buna göre, P x polinomunun x 2x 3 ile bölümünden kalan aşağıdakilerden hangisidir? A) 2x 2 B) 2x 4 C) 2x 7 D) 2x 9 E) x 1 P x x 3 .Q x 1 yazılabilir. Q x x 1 R x 2 bu polinomu yukarıya yazalım. P x x 3 . x 1 R x 2 1 olur : . P x x Çözüm 2 2 Burası tam bölünür 3 x 1 R x 2 x 3 1 x 2x 3 R x 2x 6 1 x 2x 3 R x 2x 7 Kalan 2x 7 buluruz. www.matematikkolay.net 34
2 2 Üçüncü dereceden bir P x polinomu x 2x 1 ile tam bölünebiliyor. P x polinomunun x x 2 ile bölümünden kalan 4x 8 olduğuna göre P x polinomunun baş katsayısı kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 www.matematikkolay.net 2 Derecesi 1 olmalı 2 2 P(x) x x 2 Q(x) 4x 8 miş x 2x 1 ‘e bölündüğünde kalan 0 mış. x 2x 1 ya : Çözüm 2 2x 1 ax b 2 2x 1 zıldığında, Polinom 0 çıkmalıdır. x x 2 Q(x) 4x 8 0 2x 1 x 2 Q(x) 4x 8 0 x 3 Q(x) 4x 8 0 (x 3)(ax b) 4x 8 0 a x bx 3ax 3b 4x 8 0 2ax a bx 3ax 3b 4x 8 0 x(2a b 3a 4) a 3b 8 0 x.( a b 4) (a 3b 8) 2 0 a b 4 0 a 3b 8 0 taraf tarafa toplayalım. 4b 4 0 b 1 a 5 tir. P(x) x x 2 5x 1 4x 8 Baş katsayısı 5 tir. 22
2 3 2 P x polinomunun x 3x 4 ile bölümünden kalan x 1 olduğuna göre, P x polinomunun x 3x 4 ile bölümünd en kalan aşağıdakilerden hangisidir? A) 17x 15 B) 17x 21 C) 17x 23 D) 15x 17 E) 15x 21 2 3 2 P x polinomunun x 3x 4 ile bölümünden kalan x 1 ise P x ‘ün x 3x 4 ile bölümünden : kalanı bulm Çözüm 3 3 2 2 2 2 2 3x 4 3x 4 ak için kalanın kübünü alıp, bu ifadenin kalanına bakmak yeterlidir. x 1 x 3x 3x 1 dir. kalanı polinom bölmesiyle bulabileceğimiz gibi x 3x 4 0 x 3x 4 yazarak da bulabiliriz. x. x 3. x 3x 1 2 2 3x 4 3x 4x 9x 12 3x 1 3 x 8x 11 9x 12 8x 11 17x 23 bulunur. 77
2 Katsayılar toplamı 3 ve sabit terimi 2 olan bir P x polinomunun, x x ile bölümünden kalan aşağıdaki lerden hangi – sidir? A) 5x 2 B) 5x 2 C) 3x 2 D) 3x 2 E) 4x 2 www.matematikkolay.net 2 Katsayılar toplamı 3 ise P(1) 3 tür. Sabit terim 2 ise P(0) 2 dir. P x in x x ile : Çözüm 2 2 bölümünden kalan ax b şeklinde bir polinom olacaktır. Yani; P x Q x x x ax b olarak yazabiliriz. hem x 0 için hem de x 1 için x x ifadesi 0 olduğundan bunları kullandığımızda sadece ax b kalacaktır. O ha 2 0 2 biliyoruz 0 2 2 bulduk 3 biliyoruz 0 lde; P 0 Q 0 0 0 a.0 b 2 b dir. P 1 Q 1 1 1 a.1 b 3 a 2 a 5 tir. Buna göre; ax b 5x 2 buluruz. 79
www.matematikkolay.net P x polinomunun, x 1 ile bölümünden kalan 6, x 1 ile bölümünden kalan 2, x 2 ile bölümünden kalan 3 t 2 2 2 2 2 2 ür. P x polinomunun x 1 . x 2 ile bölümünden kalan nedir? A) 4x 2 B) x x 4 C) x 2x 3 D) x 2x E) x 3x 5 2 Kalan polinom Ax Bx C olsun. P(1) 6 A B C 6 P( 1) 2 A B C 2 P( 2) 3 4 : A Çözüm 2 4 2B C 3 Bu üç denklemi çözelim. A B C 6 A B C 2 2A 2C 8 A C 4 tür. A B C 6 B 2 dir. 4A 2B C 3 4A 4 C 3 3A A C 7 1 2 2 3A 3 A 1 dir. A C 4 C 3 tür. O halde; Ax Bx C x 2x 3 buluruz. www.matematikkolay.net 24

