Soru Sor sayfası kullanılarak Polinomlar konusu altında Polinomda Kalan Bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU
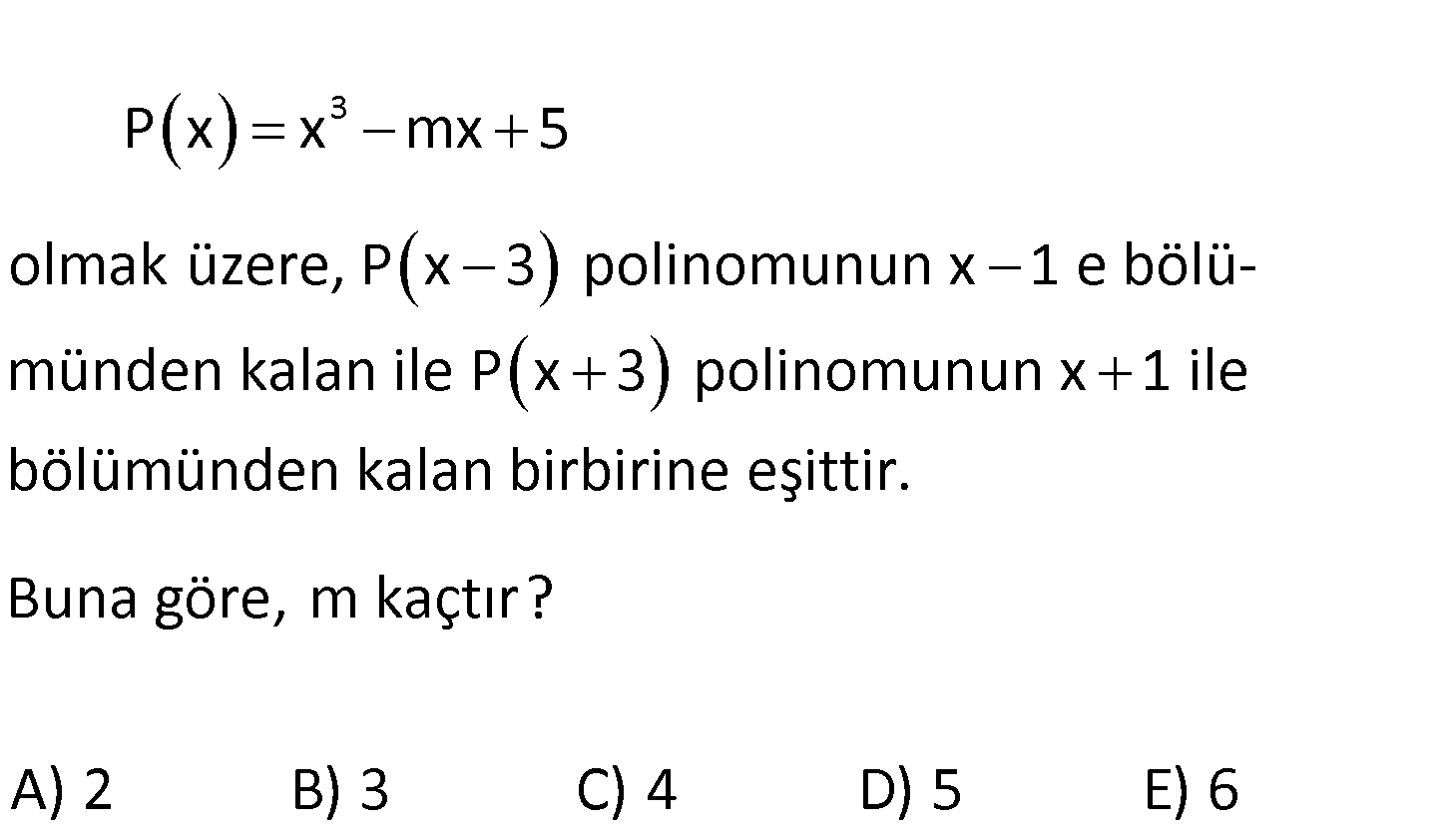

4.SORU


5.SORU


6.SORU
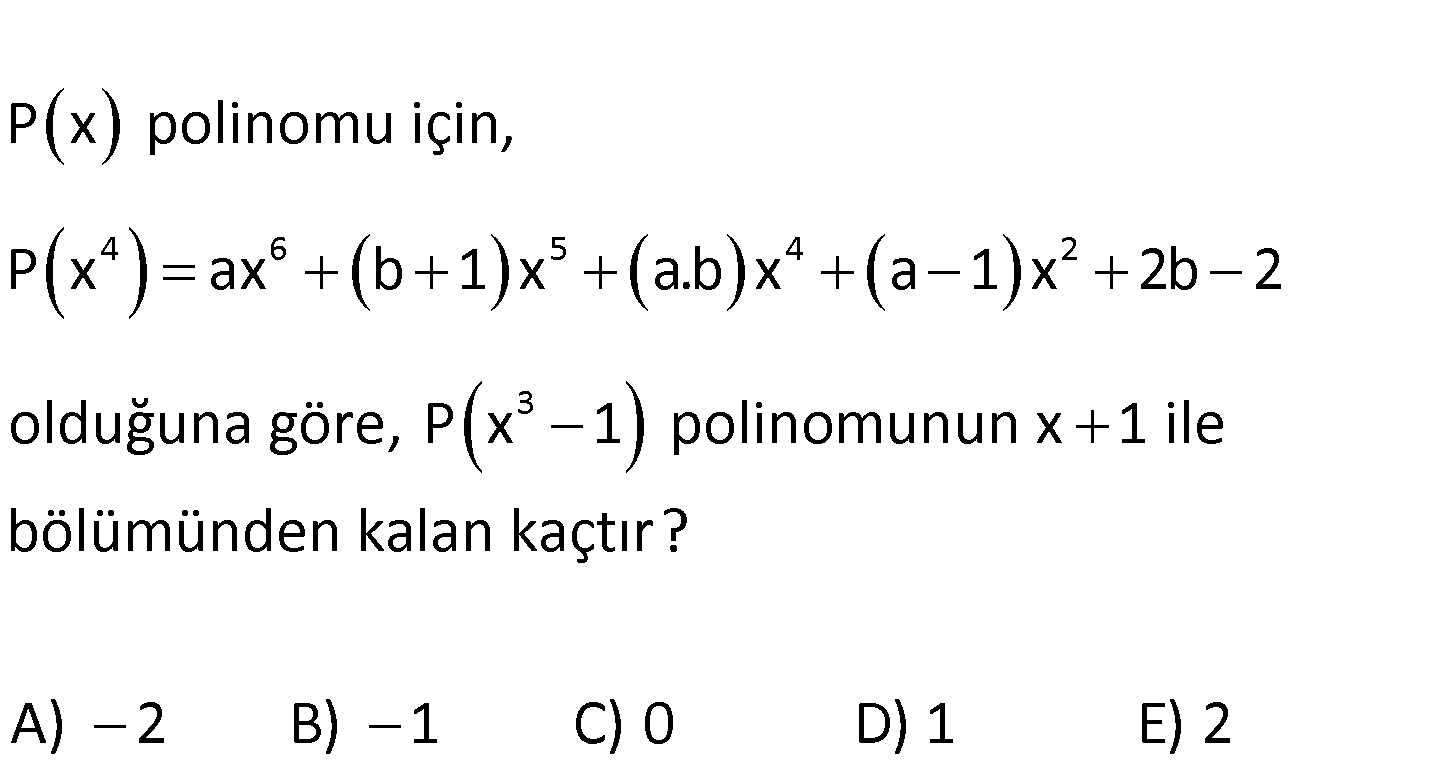

7.SORU


8.SORU
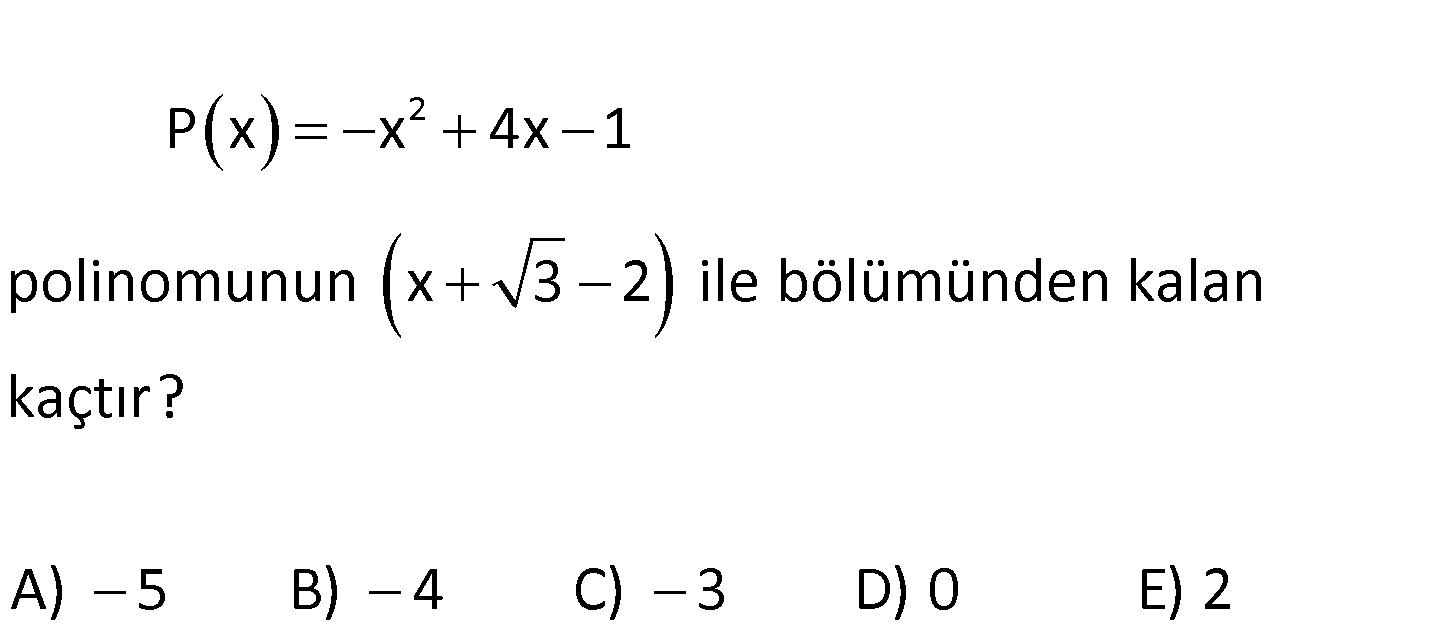

9.SORU
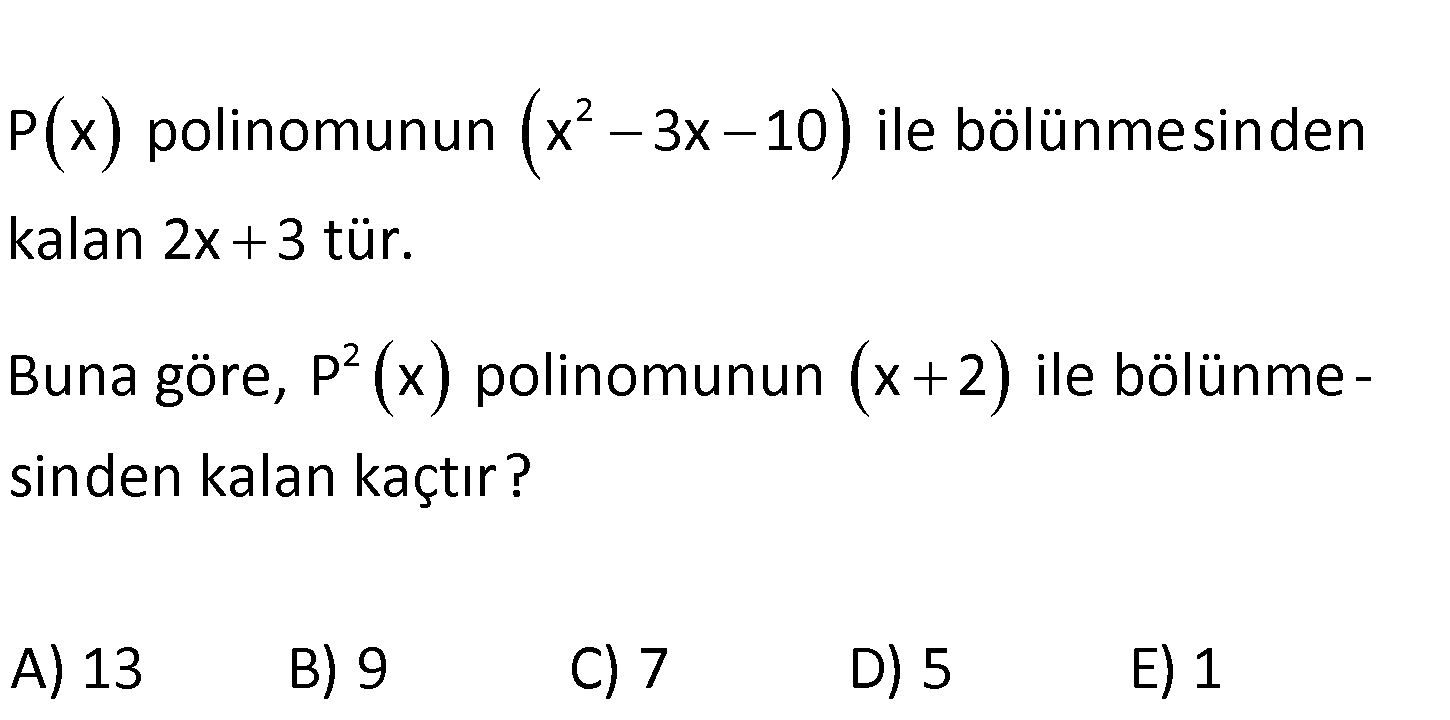

10.SORU


11.SORU


12.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 2 P x 25x 10x.P x bağıntısı veriliyor. Buna göre, P x 2 polinomunun x 2 ile bölünmesinden kala n kaçtır? A) 5 B) 10 C) 15 D) 20 E) 25 www.matematikkolay.net 2 2 P(x 2) nin x 2 ile bölümünden kalan için x 2 yazılır. Biz, P x 2 P(4) ‘ü b l : u Çözüm 2 2 2 2 2 malıyız. P x 25x 10x.P(x) denkleminde x 4 yazarsak; P 4 400 40.P(4) P 4 40.P(4) 400 0 P 4 20 0 P(4) 20 buluruz. Cevap: D 52
www.matematikkolay.net 3 Üçüncü dereceden bir P x polinomu x 4x ile kalansız bölünebilmektedir. P x in x 1 ile bölünmesinden k alan 12 olduğuna göre, x 3 ile bölünmesinden kalan kaçtır? A) 60 B) 40 C) 35 D) 25 E) 10 3 P x x 4x Q x şeklinde bir polinomdur. P x polinomu 3.dereceden bir polinom ise; Q x k gibi bir : Çözüm 3 3 3 3 sayısal değere eşit olmalıdır. Yoksa polinomun derecesi artar. P x k x 4x yazabiliriz. P(1) 12 ise P 1 k 1 4.1 12 3k k 4 tür. Buna göre; P x 4 x 4x tir. x 3 ile bölümünden kalan; P 3 4 3 4.3 4 27 12 415 60 buluruz. 54
3 P x x mx 5 olmak üzere, P x 3 polinomunun x 1 e bölümünden kalan ile P x 3 polinomunun x 1 i le bölümünden kalan birbirine eşittir. Buna göre, m kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 www.matematikkolay.net 1 P(x 3) ün (x 1) ile bölümünden kalanı bulurken, x 1 0 x 1 için P(x 3) P( 2) he : sapl Çözüm 1 3 3 anır. P(x 3) ün (x 1) ile bölümünden kalanı bulurken, x 1 0 x 1 için P(x 3) P(2) hesaplanır. P( 2) P(2) ise ( 2) m.( 2) 5 (2) m.(2) 5 8 2m 5 8 2m 5 2m 3 2m 13 2m 2m 13 3 4m 16 m 4 buluruz. 98
3m 5 m m P(x) 2x x k polinomunun x 2 ile bölümünden kalan 6 olduğuna göre k kaçtır? A) 18 B) 1 2 C) 14 D) 22 E) 30 3m 5 m m 5 3 m m 5 3 5 5 P(x) 2x x k P(x) 2x x k Polinom belirtmesi için m -5 olmalıdır. P(x) 2x x k : Çözüm 2 5 2 5 2x x k olur. x 2 ile bölümünden kalan 6 ise P( 2) 6 dır. O halde; P( 2) 2 2 2 k 6 8 32 k 6 24 k k 30 buluruz. 44
2 P x polinomunun x x ile bölümünden kalan x 4 olduğuna göre, P x polinomunun x 1 ile bölümünden kala n kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 2 P(x) x x Q(x) x 4 şeklinde yazabiliriz. x 1 ile bölümünden kalanı bulmak için; x : 1 0 x 1 Çözüm 0 0 yazalım. P( 1) 1 1 Q( 1) 1 4 P( 1) 1 4 3 buluruz. www.matematikkolay.net 38
4 6 5 4 2 3 P x polinomu için, P x ax b 1 x a.b x a 1 x 2b 2 olduğuna göre, P x 1 polinomunun x 1 ile bölümünden kalan kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 4 8 5 4 2 3 P(x ) ax (b 1)x (a.b)x (a 1)x 2b 2 P(x 1) polinomunun x 1 ile bölümünden kalanı bulmak ç : i Çözüm 3 4 4 4 2 4 2 2 2 in; x 1 0 x 1 dir. P(( 1) 1) P( 2) bulunmalı. x 2 yazalım. P(x ) a x (b 1)x .x (a 1).x 2b 2 a.(2) (b 1).2.x (a 1)x 2b 2 14
2 İkinci dereceden bir P x polinomunun x 3 ile bölümünden kalan x 2 dir. P x polinomunun x 1 ile bölümü nden kalan 4 olduğuna göre, x 1 ile bölümünden kalan kaç – tır? A) 3 B) 2 C) 1 D) 2 E) 3 www.matematikkolay.net 2 P(x) polinomu 2.dereceden bir polinom olduğundan P(x) a.(x 3) x 2 yazılabilir. P(x) poli o : n m Çözüm 2 2 unun (x 1) ile bölümünden kalan 4 olduğuna göre; P(1) 4 olmalı. P(1) 4 a.(1 3) 1 2 4 4a 3 4 1 a ‘ tür. 4 1 P(x) (x 3) x 2 olur. 4 P(x) polinomun x 1 ile bölümünden kalanı bulabilmek için x 1 yazılmalı. P( 2 1 1) (( 1) 3) 1 2 4 1 P( 1) 4 4 1 2 bulunur. 20
www.matematikkolay.net 2 P x x 4x 1 polinomunun x 3 2 ile bölümünden kalan kaçtır? A) 5 B) 4 C) 3 D) 0 E) 2 2 2 2 2 P(x) x 4x 1 3 çıkarıp, 3 ekleyelim P(x) x 4x 1 3 3 P(x) x 4x 4 3 P(x) x 4x 4 3 P( : Çözüm 2 x) x 2 3 tür. x 3 2 0 x 2 3 tür. x 2 3 için P(x) 2 3 2 2 3 P(x) 3 3 P(x) 0 buluruz. Cevap: 0 47
2 2 P x polinomunun x 3x 10 ile bölünmesinden kalan 2x 3 tür. Buna göre, P x polinomunun x 2 ile bölünme – sinden kalan kaçtır? A) 13 B) 9 C) 7 D) 5 E) 1 www.matematikkolay.net 2 05.Şub 2 x 3x 10 x 5 x 2 dir. Yani x 2 ; x 3x 10 ifadesinin bir çarpanıdır. Bu sebepl : e P( Çözüm 2 2 2 2 x) 2x 3 kabul edebiliriz. P (x) 2x 3 dir. x 2 ile bölümünden kalanı bulmak için x 2 yazalım. 2. 2 3 1 1 buluruz. 49
P x 3 polinomunun x 1 ile bölümünden kalan 4, Q 2x 1 polinomunun x 2 ile bölümünden kalan 2, K x x 2 2 .P 5x 6 Q x 1 . 3x 2 olduğuna göre, K 3x 5 polinomunun x 1 ile bölümünden kalan kaçtır? A) 2 B) 4 C) 8 D) 16 E) 32 www.matematikkolay.net 1 1 P(x 3) polinomunun x 1 ile bölümünden kalan 4 ise x 1 0 P(x 3) 4 P( : 4) 4 tür. Q(2x Çözüm 2 2 1 1 2 2 1) polinomunun x 2 ile bölümünden kalan 2 ise x 2 0 Q(2x 1) 2 Q(5) 2 dir. K(3x 5)’in x 1 ile bölümünden kalanı bulmak için; x 1 0 K(3 x 5) K(2)’yi bulmalıyız. K(x) x P(5x 6) Q x 1 . 3x 2 x 2 yazalım. K(2) 4.P(5.2 6) Q 4 1 . 3.2 2 K(2) 4.P(4) Q 5 . 4 K(2) 4.4 2.4 16 8 8 buluruz. 61
n 1 n 2 2 n 1 x n 2 x … 2x x polinomunun 4x 4 ile bölümünden kalan 66 olduğuna göre, 3x 3 ile bölünür se kalan kaç olur? A) 12 B) 6 C) 0 D) 6 E) 10 4x 4 0 x 1 yazılarak kalan bulunur. x 1 yazınca; n 1 n 2 … 2 1 66 ol : uyorsa n 1 n 66 2 Çözüm 11.12 11 10 2 11 10 2 1 1 1 n 1 n 132 n 12 dir. P(x) 11x 10.x … 2x x olur. 3x 3 0 x 1 yazılarak kalan bulunur. x 1 yazınca; P( 1) 11( 1) 10.( 1) … 2( 1) ( 1) 11 10 9 8 7 6 1 1 5 4 3 2 1 6 buluruz. 70
www.matematikkolay.net P x ve Q x polinomlarının x 2 ile bölümlerinden kalanlar sırasıyla 4 ve 1 dir. k.P x 4.Q x po linomunun çarpanlarından biri x 2 olduğuna göre, k kaçtır? A) 2 B) 1 C) 1 D) 2 E) 3 x 2 ile bölümünden kalanlar verilmiş. x 2 0 x 2 dir. P( 2) 4 ve Q( 2) 1 dir. kP( Q : x) 4 Çözüm 4 1 (x) polinomu x 2 ye tam bölünüyorsa; x 2 yazınca 0 çıkmalıdır. Yani; kP( 2) 4Q( 2) 0 dır. 4k 4 0 4k 4 k 1 buluruz. 46

