Soru Sor sayfası kullanılarak Parabol konusu altında Parabolün içindeki şeklin alanı ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
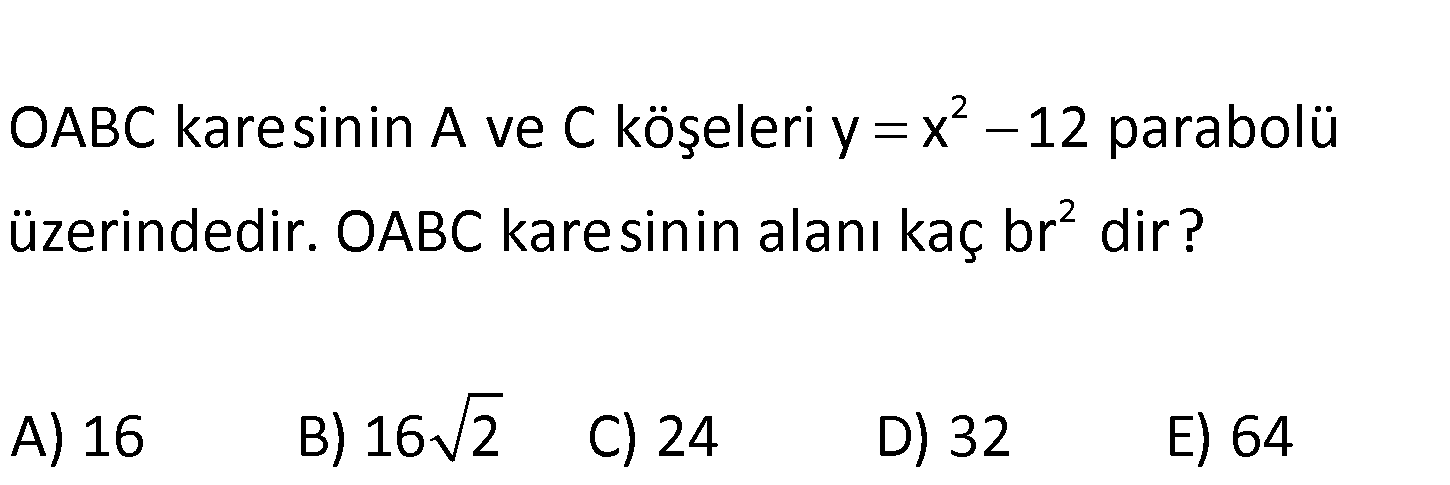

2.SORU

3.SORU

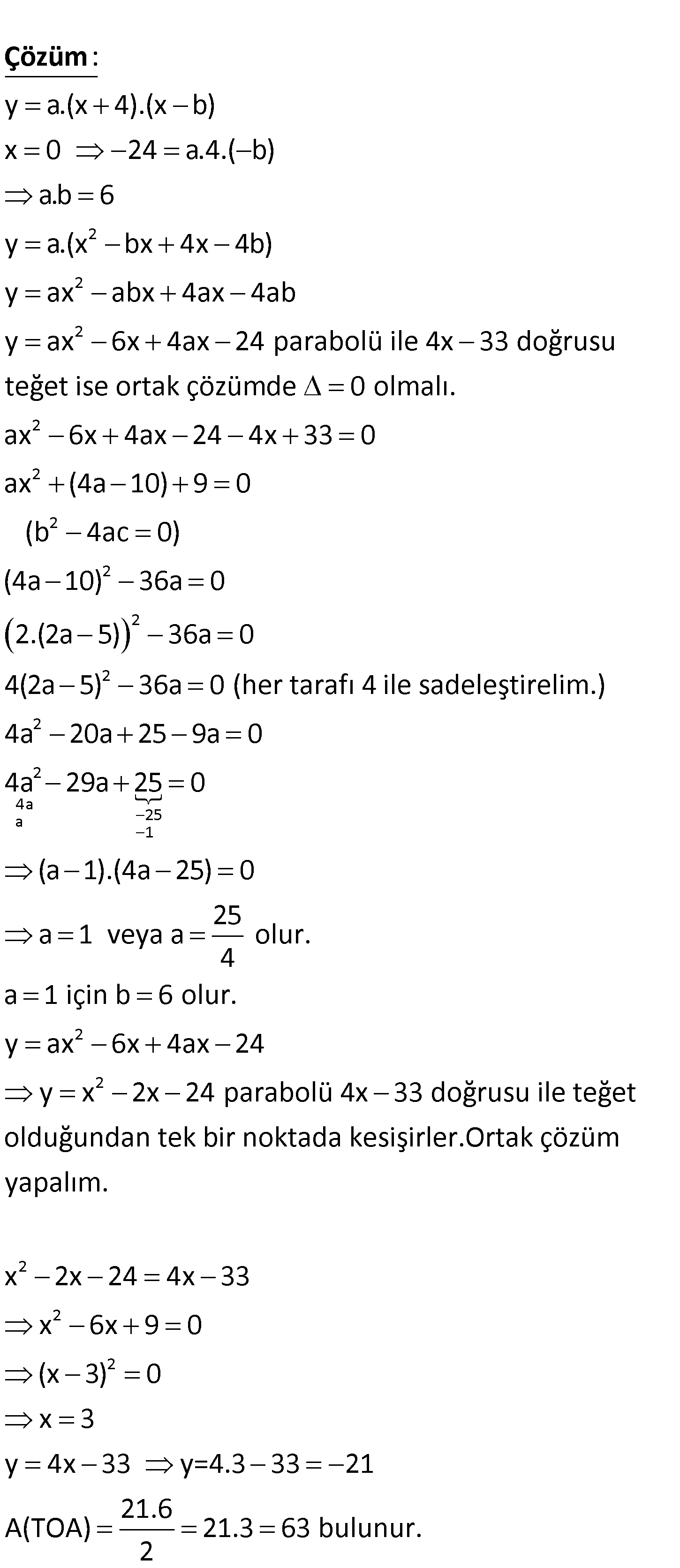
4.SORU


5.SORU


6.SORU

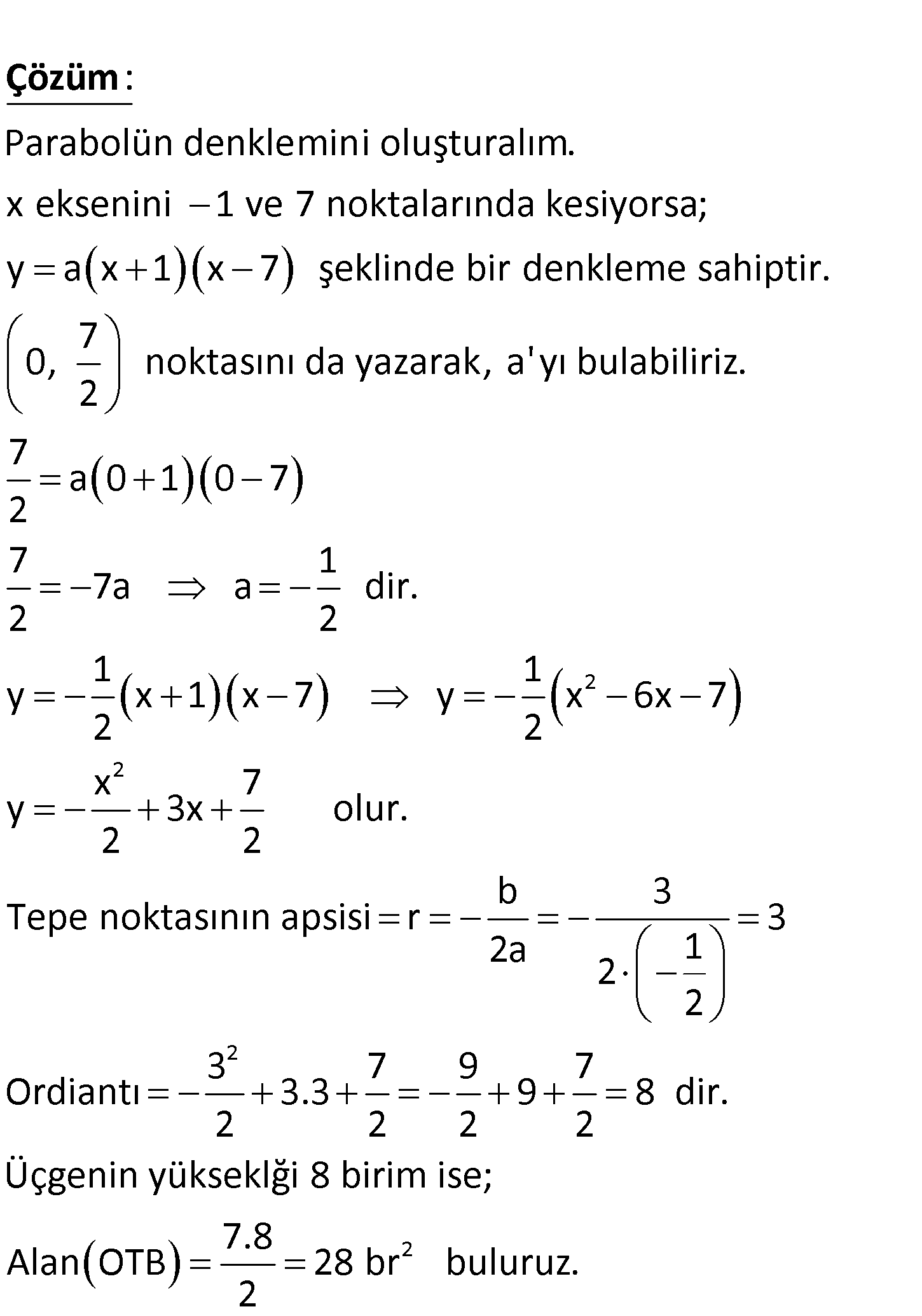
7.SORU


8.SORU


9.SORU
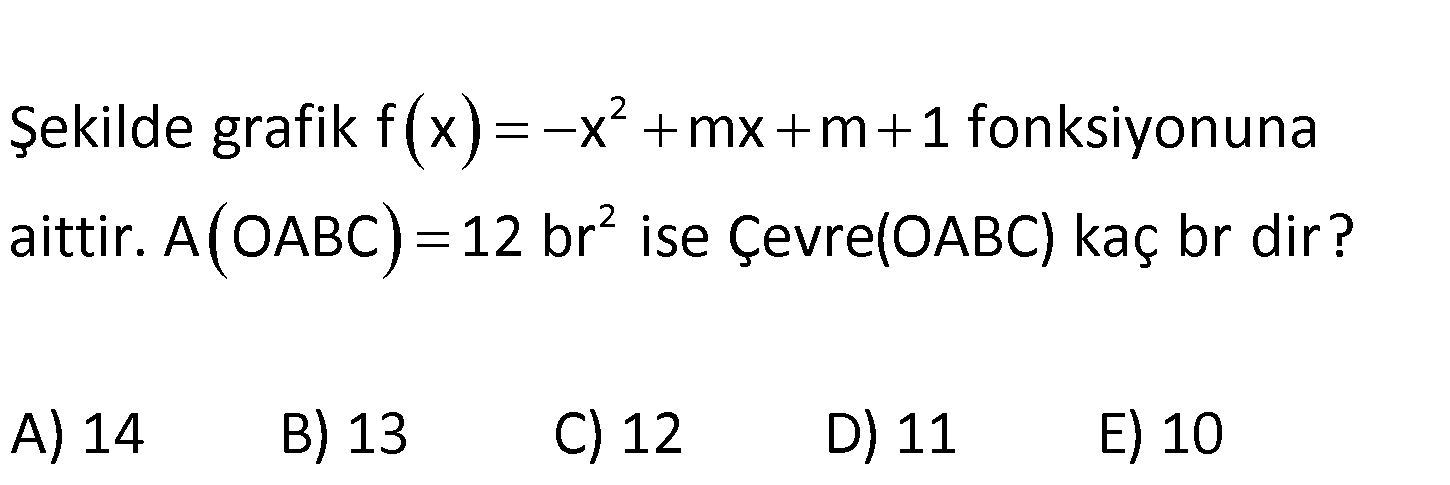
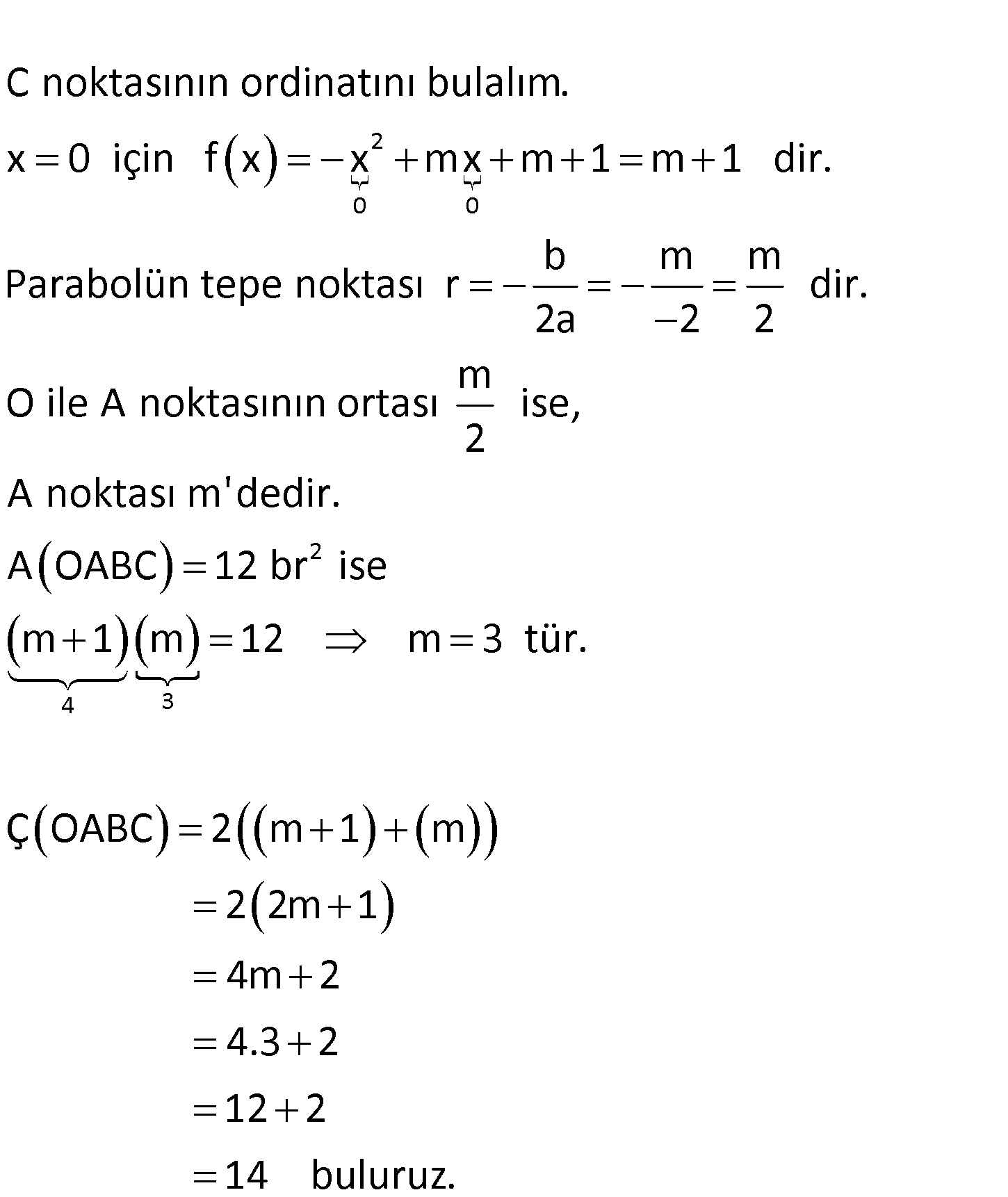
10.SORU

11.SORU


12.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
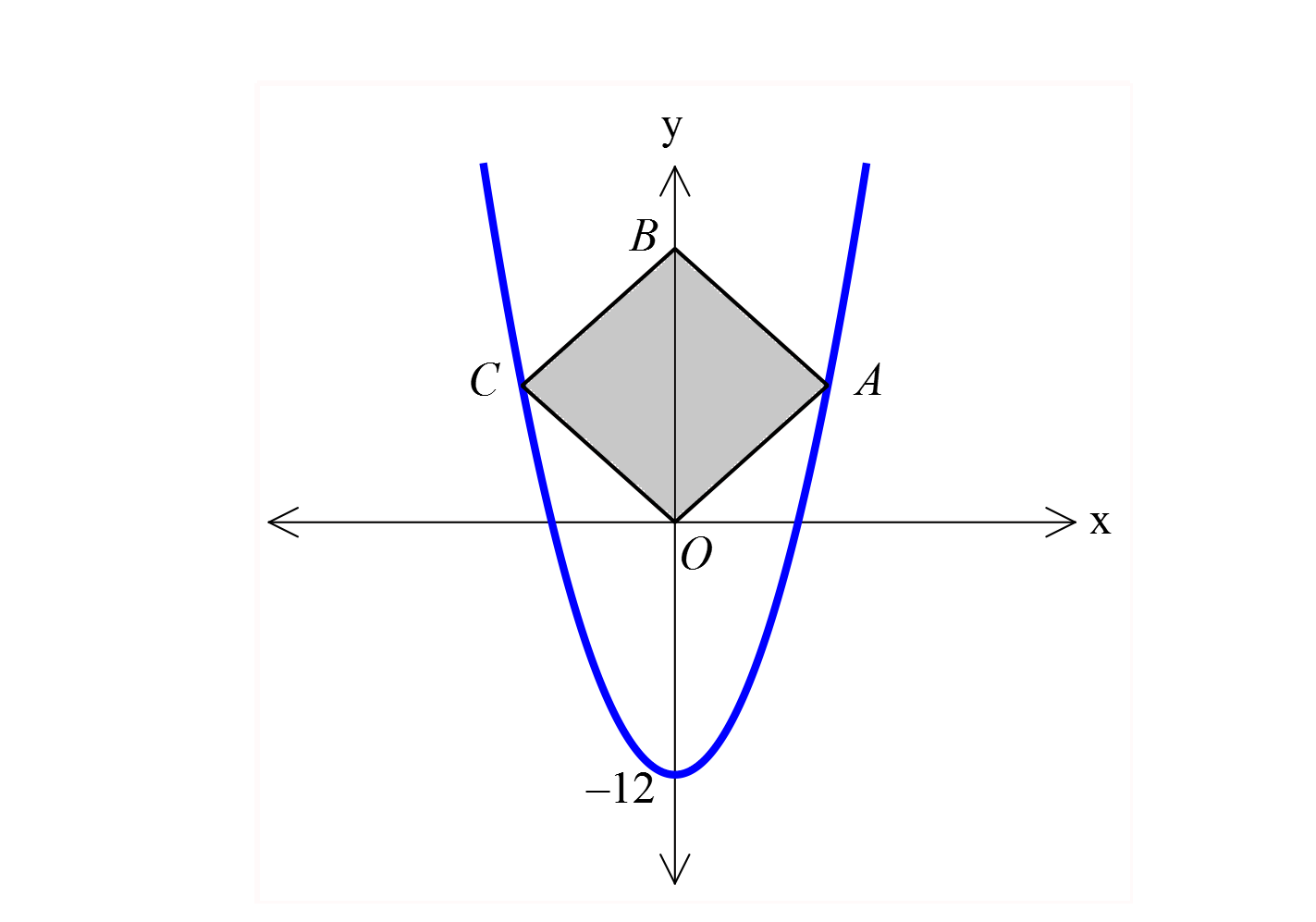
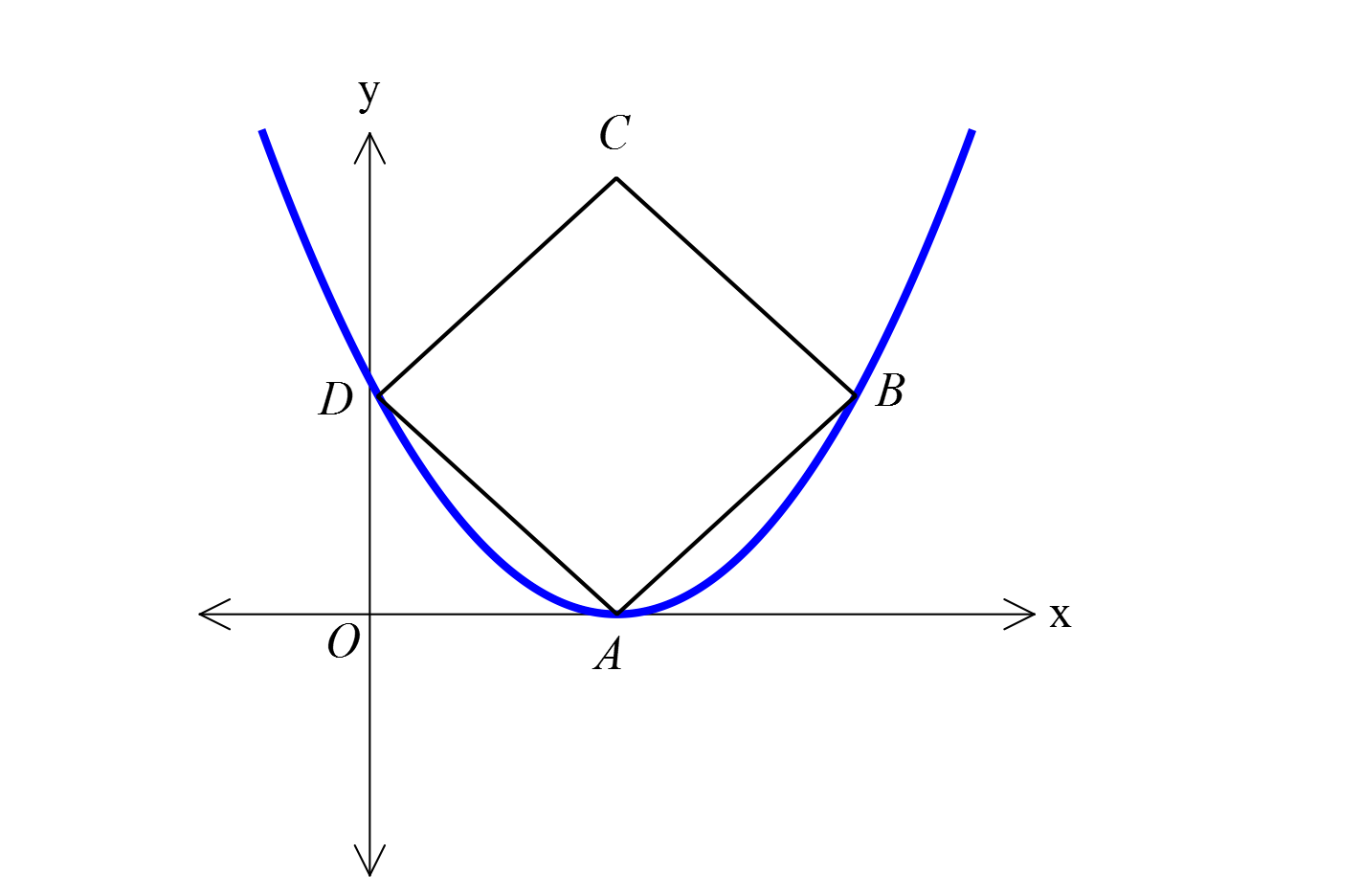
2 2 OABC karesinin A ve C köşeleri y x 12 parabolü üzerindedir. OABC karesinin alanı kaç br dir? A 16 ) B) 16 2 C) 24 D) 32 E) 64 www.matematikkolay.net 2 2 2 A noktasının apsisi x ise, ordinatı da x tir. y x 12 x x 12 0 x x 12 0 (x 4)(x 3) x 4 tür : . A Çözüm 2 noktası, (4, 4) noktası ise, karenin bir kenarı 4 2 dir. Karenin Alanı (4 2) 32 buluruz. 15
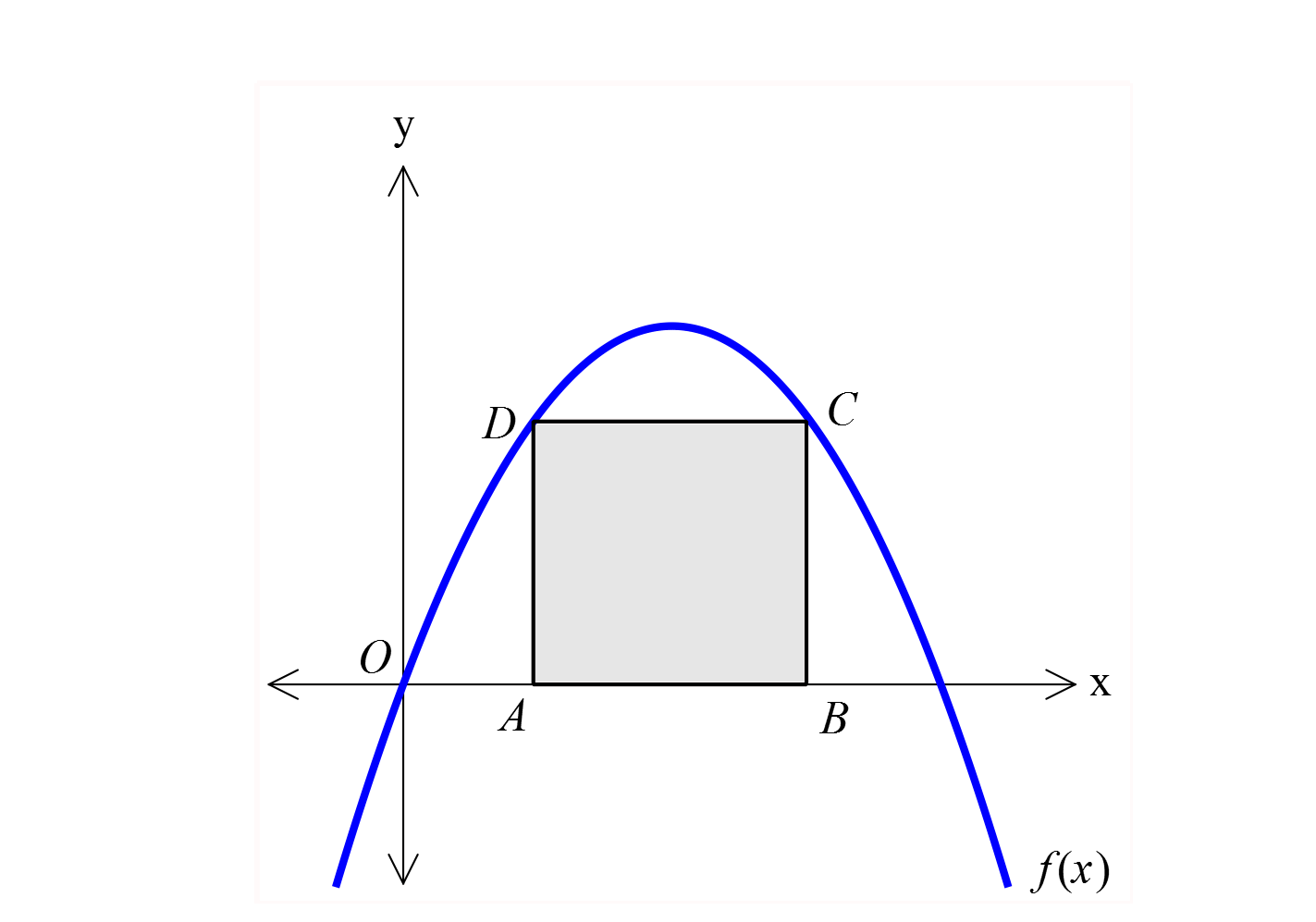
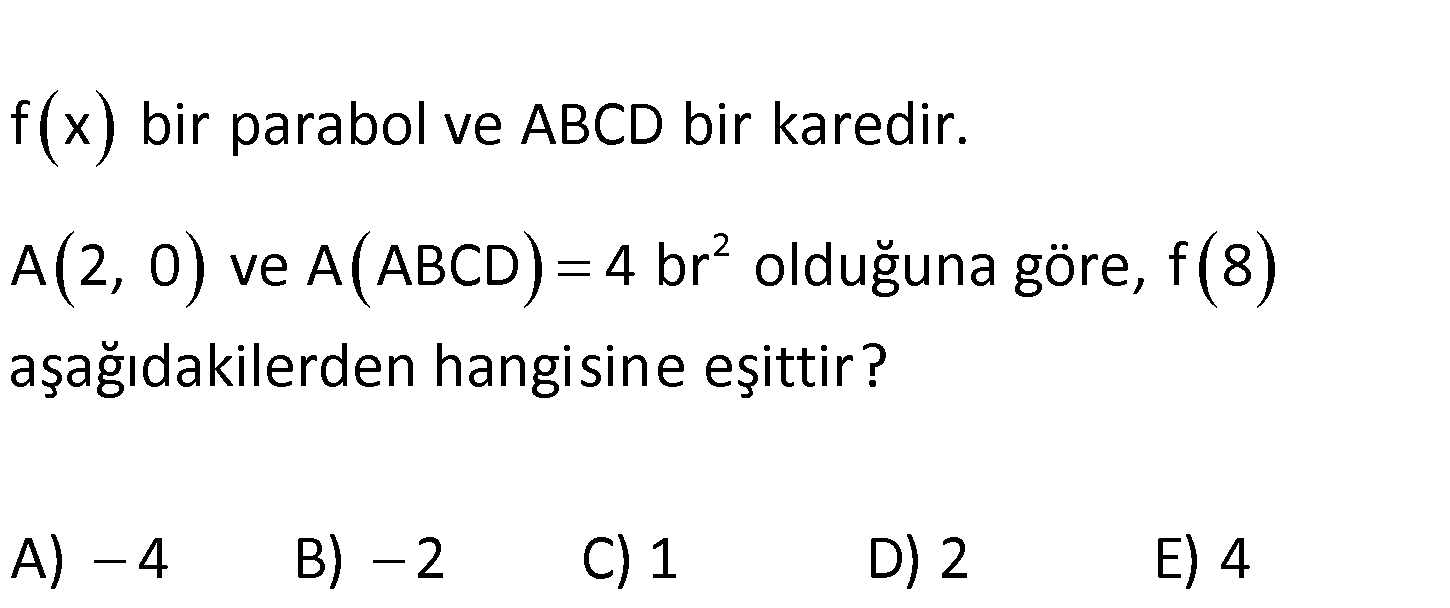
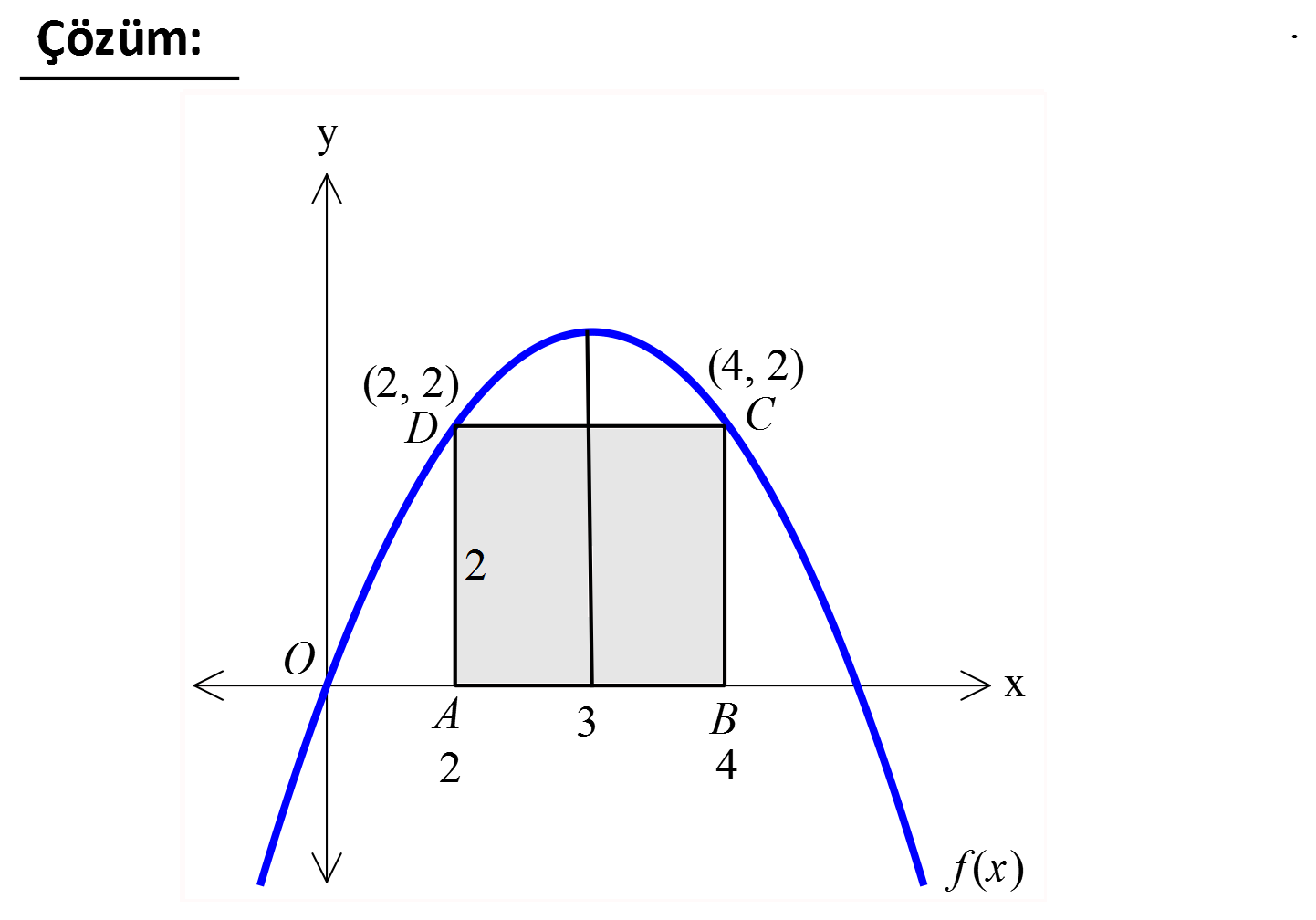
2 f x bir parabol ve ABCD bir karedir. A 2, 0 ve A ABCD 4 br olduğuna göre, f 8 aşağıdakilerden ha ngisine eşittir? A) 4 B) 2 C) 1 D) 2 E) 4 www.matematikkolay.net Karenin alanı 4 olduğundan, bir kenarı 2 birimdir. Parabolün tepe noktasındaki x değeri 2 ile 4’ün 2 2 2 2 tam ortası yani 3′ tür. Buna göre parabol denklemi; y a(x r) k y a(x 3) k dır. (0,0) noktası bu parabolü sağlamalıdır. 0 a(0 3) k 0 9a k k 9a dır. y a(x 3) 9a (2,2) noktası da bu parabolü sa 2 2 2 ğlamalıdır. 2 a(2 3) 9a 2 a 9a 1 2 8a a tür. 4 1 9 y (x 3) tür. 4 4 1 9 f(8) (8 3) 4 4 25 9 16 4 buluruz. 4 4 4 17
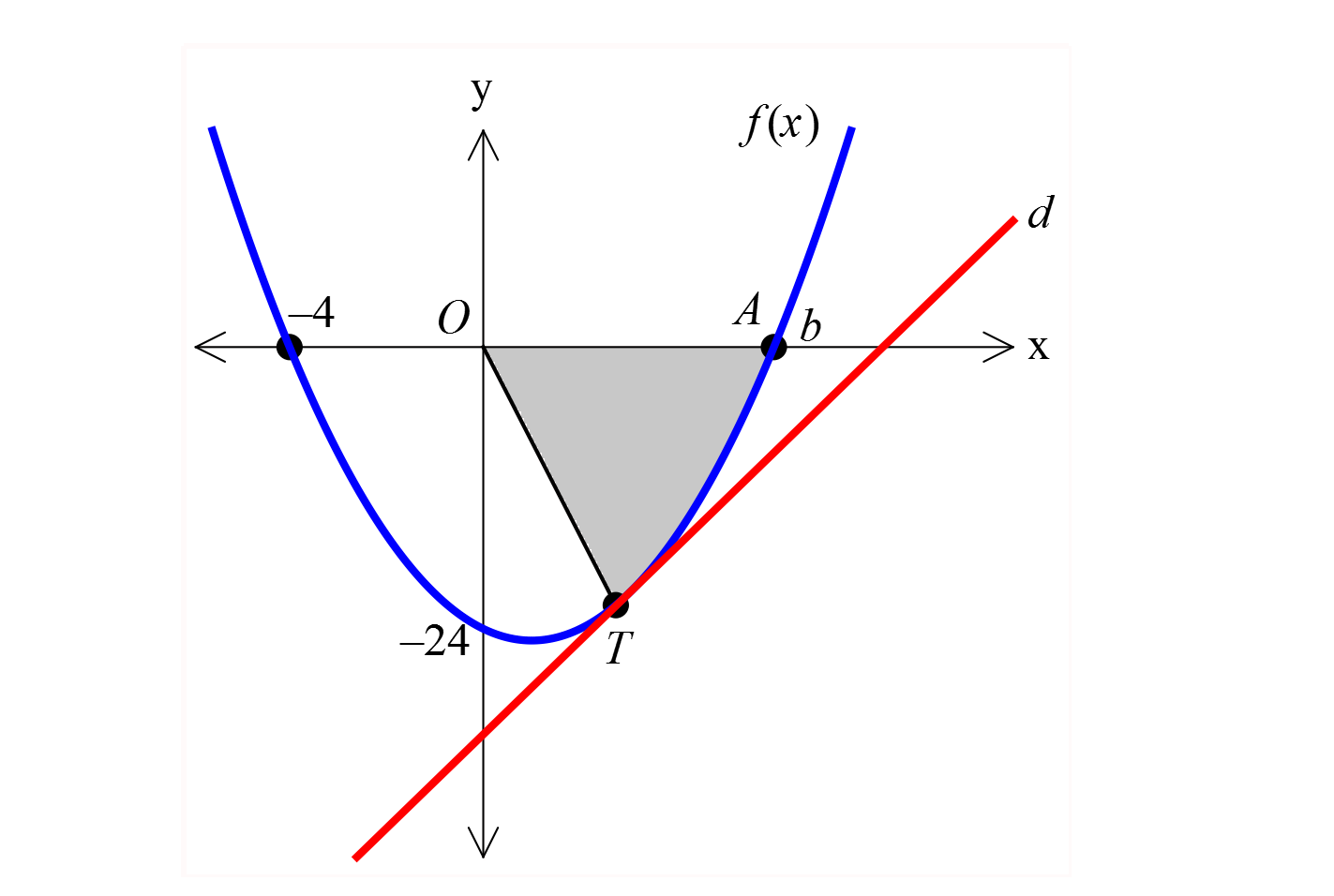
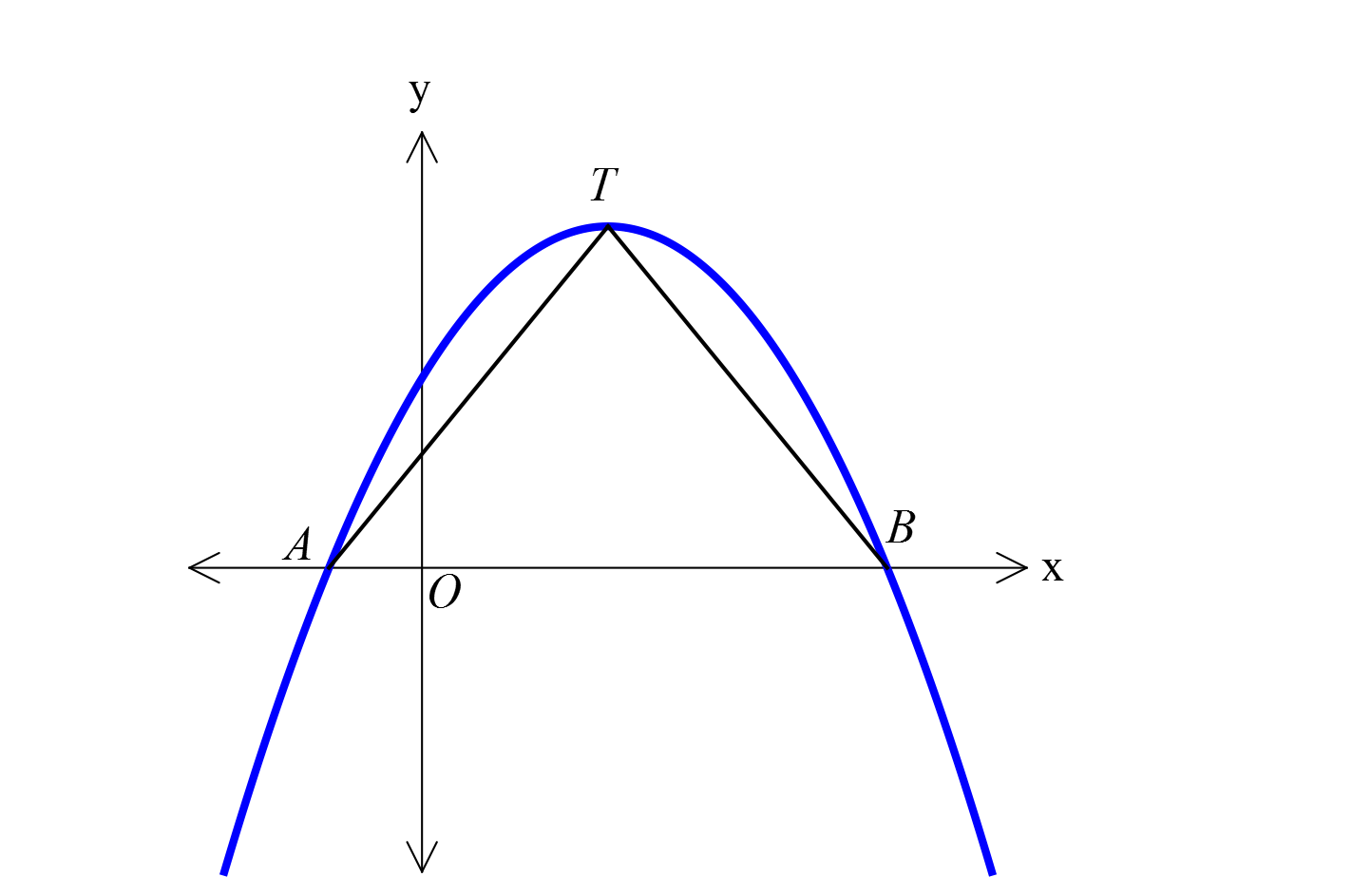
www.matematikkolay.net y f x parabolü d 4x 33 doğrusuna T noktasın – da teğettir. Buna göre, TOA üçgeninin alanı kaç birimkar A) 63 B) 64 C) 65 D) 66 E) 67 edir? www.matematikkolay.net 2 2 2 y a.(x 4).(x b) x 0 24 a.4.( b) a.b 6 y a.(x bx 4x 4b) y ax abx 4ax 4ab y ax 6x 4 : ax 24 para Çözüm 2 2 2 2 2 2 2 bolü ile 4x 33 doğrusu teğet ise ortak çözümde 0 olmalı. ax 6x 4ax 24 4x 33 0 ax (4a 10) 9 0 (b 4ac 0) (4a 10) 36a 0 2.(2a 5) 36a 0 4(2a 5) 36a 0 (her tarafı 4 ile sadeleştirelim.) 4a 20a 25 9 2 4a a 25 1 2 2 2 a 0 4a 29a 25 0 (a 1).(4a 25) 0 25 a 1 veya a olur. 4 a 1 için b 6 olur. y ax 6x 4ax 24 y x 2x 24 parabolü 4x 33 doğrusu ile teğet olduğundan tek bir noktada kesişirler.Ortak çözüm yapalım. x 2x 2 2 24 4x 33 x 6x 9 0 (x 3) 0 x 3 y 4x 33 y=4.3 33 21 21.Haz A(TOA) 21.3 63 bulunur. 2 www.matematikkolay.net 34
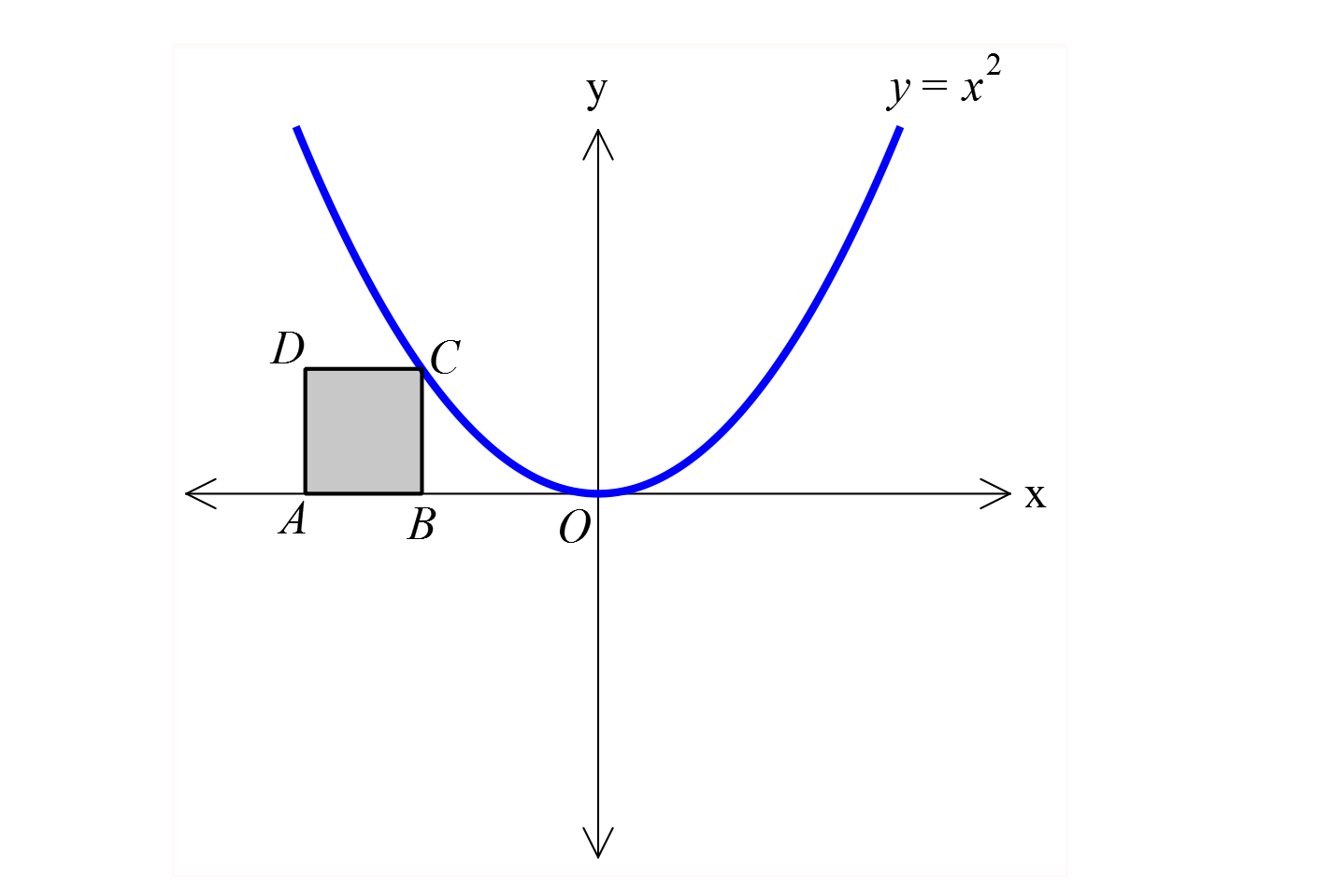
2 2 Şekildeki ABCD karesinin C köşesi y x parabolü üzerindedir. A 6, 0 olduğuna göre, A ABCD kaç br ir d ? A) 4 B) 9 C) 16 D) 25 E) 36 www.matematikkolay.net 2 2 a pozitif bir sayı olsun. C noktasının apsisine a diyelim. Ordinatı y a dir. O halde, |BC| a : Çözüm 2 2 2 2 (3.)( 2) 2 2 2 olduğundan karenin bir kenarı a birimdir. A noktasının apsisi a a dir. Bu da 6’ya eşitse a a 6 0 a a 6 a 3 a 2 a 2 dir. Karenin bir kenarı a 2 4 tür. A(ABCD) 4 16 buluruz. 41
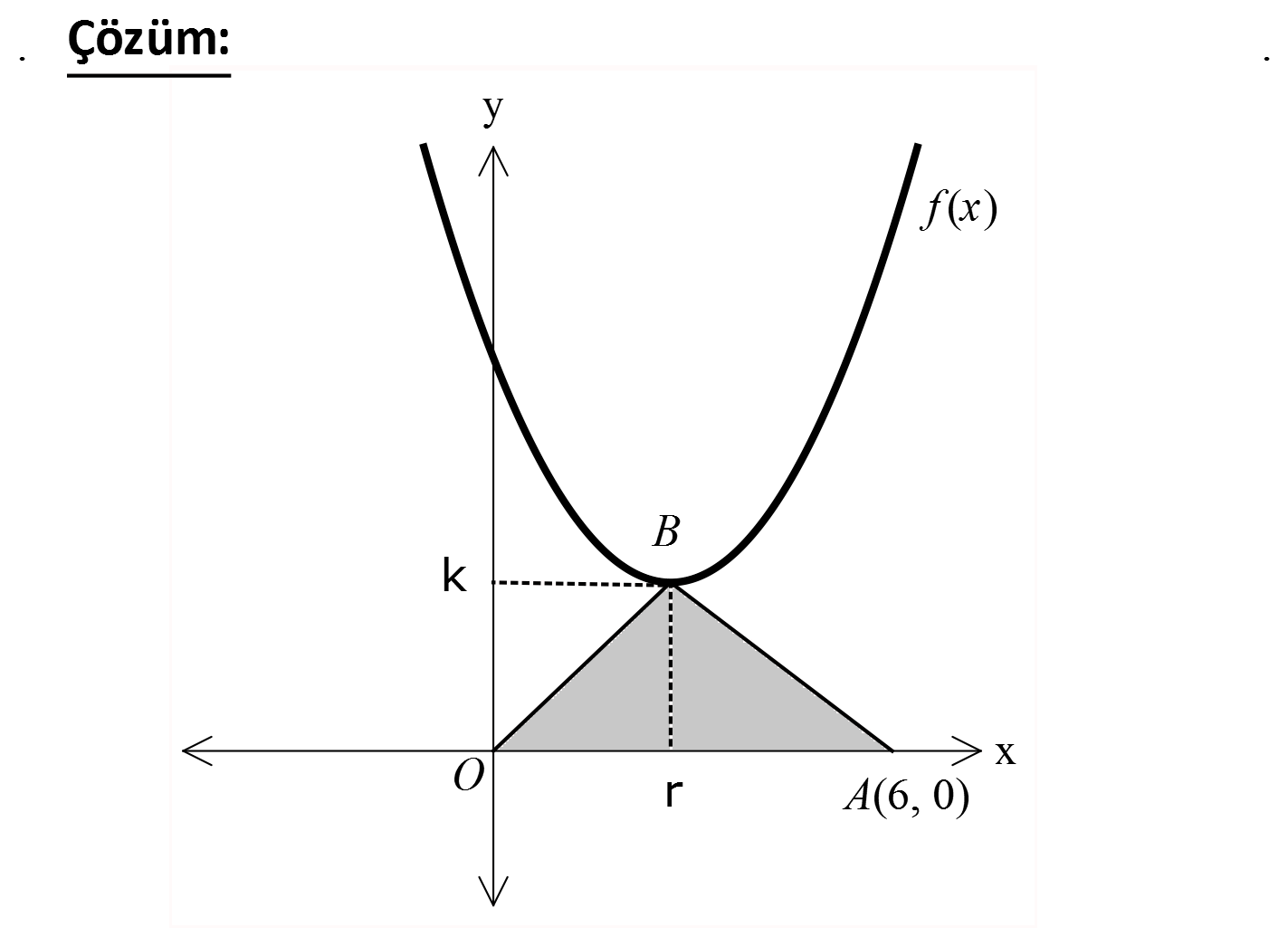
www.matematikkolay.net 2 Yukarıdaki şekilde grafiği verilen y ax bx c parabolünün tepe noktası T 2, k dır. Parabol x eksenin 2 i A ve B noktalarında kesmekte – dir. TAB eşkenar üçgeninin alanı 9 3 br olduğuna göre, a kaçtır? 3 3 3 3 A) 3 3 B) 3 C) D) E) 2 3 2 www.matematikkolay.net 2 Eşkenar üçgenin bir kenarı a birim olsun. a 3 9 3 olmalıdır. a 6 bulunur. 4 T(2,k) kt : no Çözüm asındaki k değeri, eşkenar üçgenin yükseliğidir. Eşkenar üçgenin bir kenarı 6 ise, yüksekliği 3 3 cm dir. 30 60 90 üçgeninden bulunur. O zaman T(2,3 3) noktasıdır. A ve B noktaları ise r 2 değerinden 3’er cm 6 solunda ve sağındadır. Neden 3 3 2 Buna göre A( 1,0) ve B 5,0 noktalarıdır. Parabolun denklemini; y a x 5 x 1 y a x 5 x 1 olarak yazabiliriz. T(2,3 3) noktası da bu parabolün üzerinde olduğund an; 3 3 a 2 5 2 1 eşitliğini yazabiliriz. 3 3 a 3 3 3 3 9a 3 3 3 a buluruz. 9 3 44
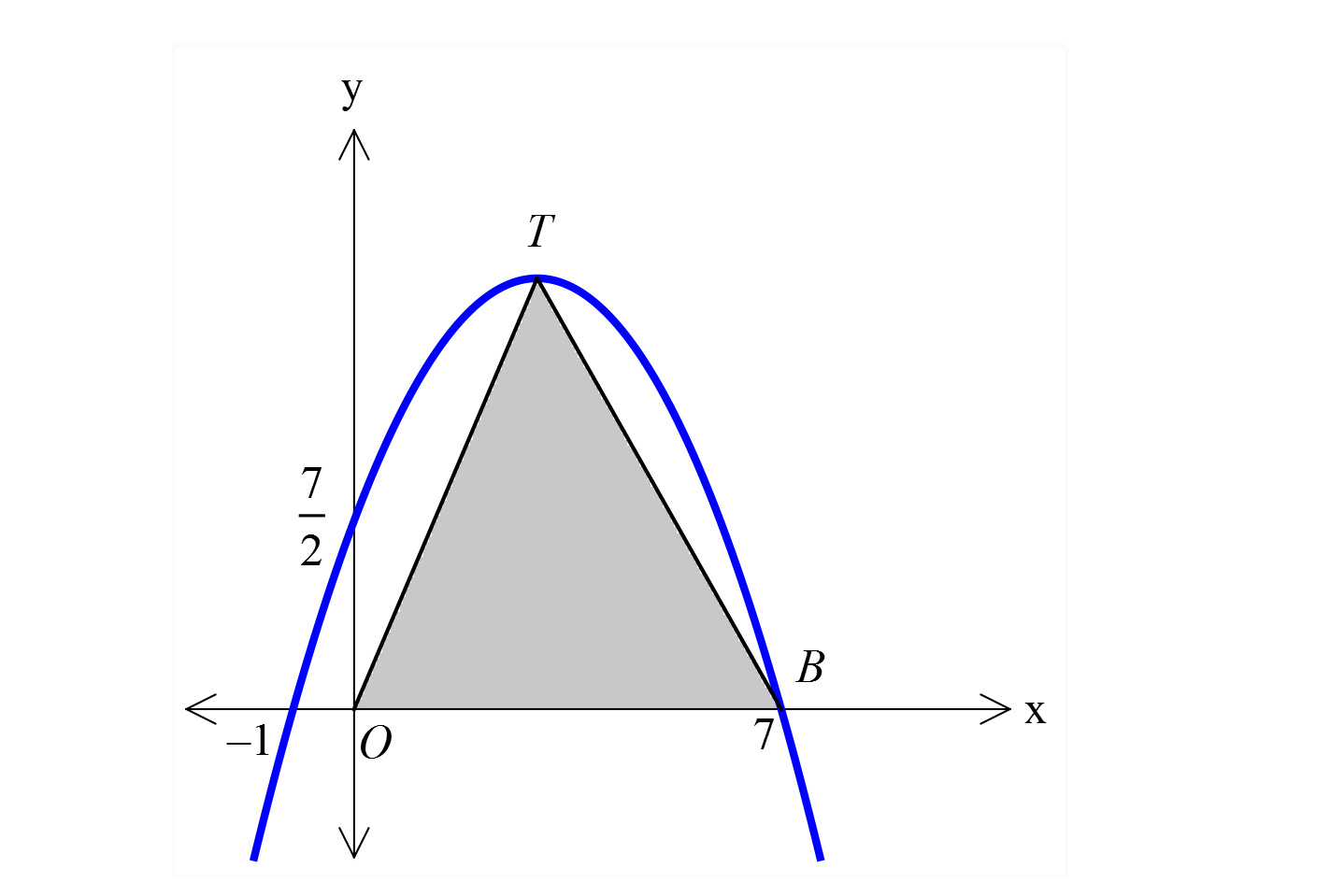
www.matematikkolay.net 2 f x ax bx c fonksiyonu x eksenini 1, 0 ve 7 7, 0 noktalarında; y eksenini 0, noktasında 2 kesm ektedir. Verilenlere göre, A AOB kaç birimkaredir? www.matematikkolay.net Parabolün denklemini oluşturalım. x eksenini 1 ve 7 noktalarında kesiyorsa; y a x 1 x 7 şekl : in Çözüm 2 2 de bir denkleme sahiptir. 7 0, noktasını da yazarak, a’ yı bulabiliriz. 2 7 a 0 1 0 7 2 7 1 7a a dir. 2 2 1 1 y x 1 x 7 y x 6x 7 2 2 x 7 y 3x olur. 2 2 b 3 Tepe noktasının apsisi r 2a 1 2 2 2 2 3 3 7 9 7 Ordiantı 3.3 9 8 dir. 2 2 2 2 Üçgenin yükseklği 8 birim ise; 07.Ağu Alan OTB 28 br buluruz. 2 52
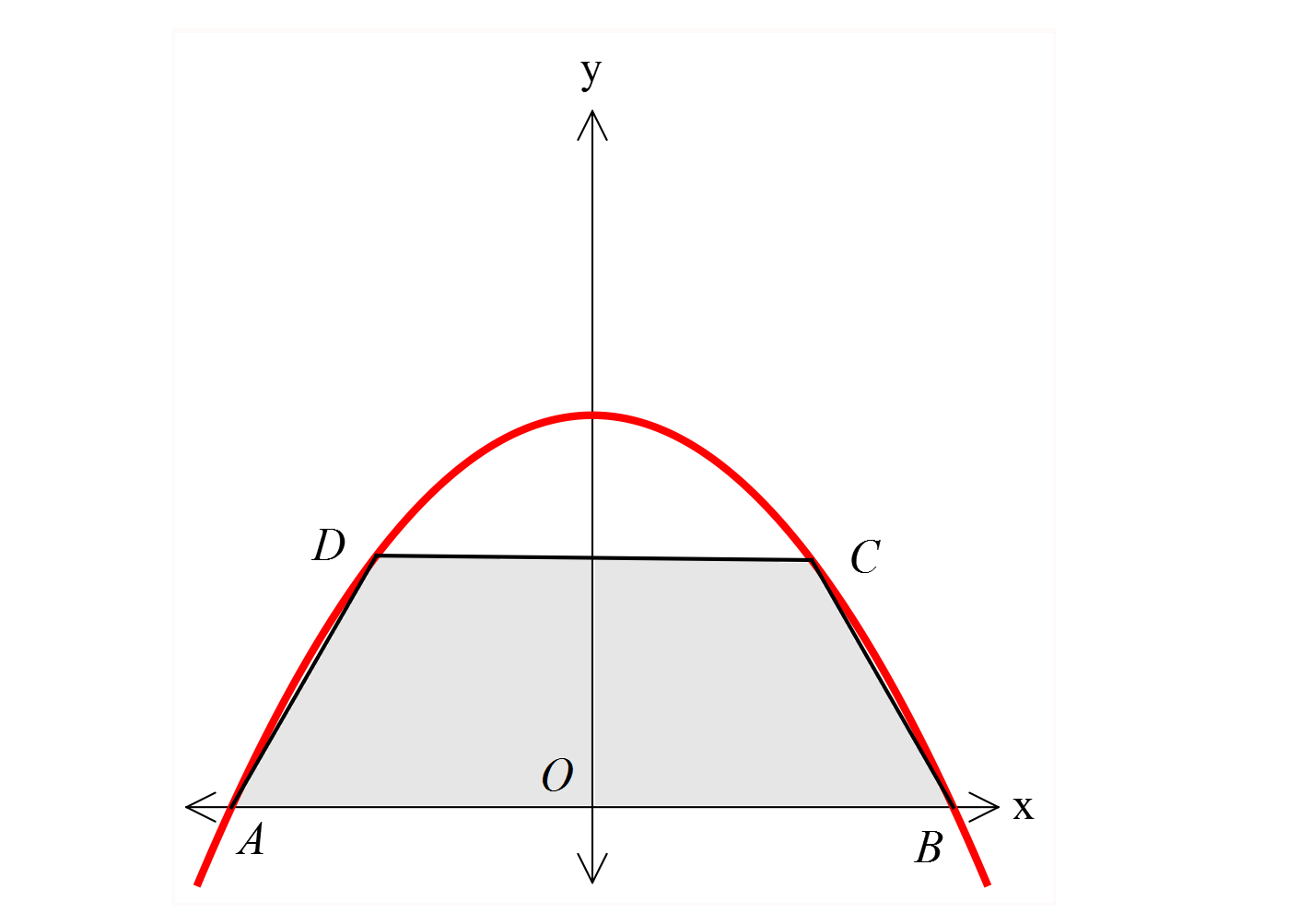
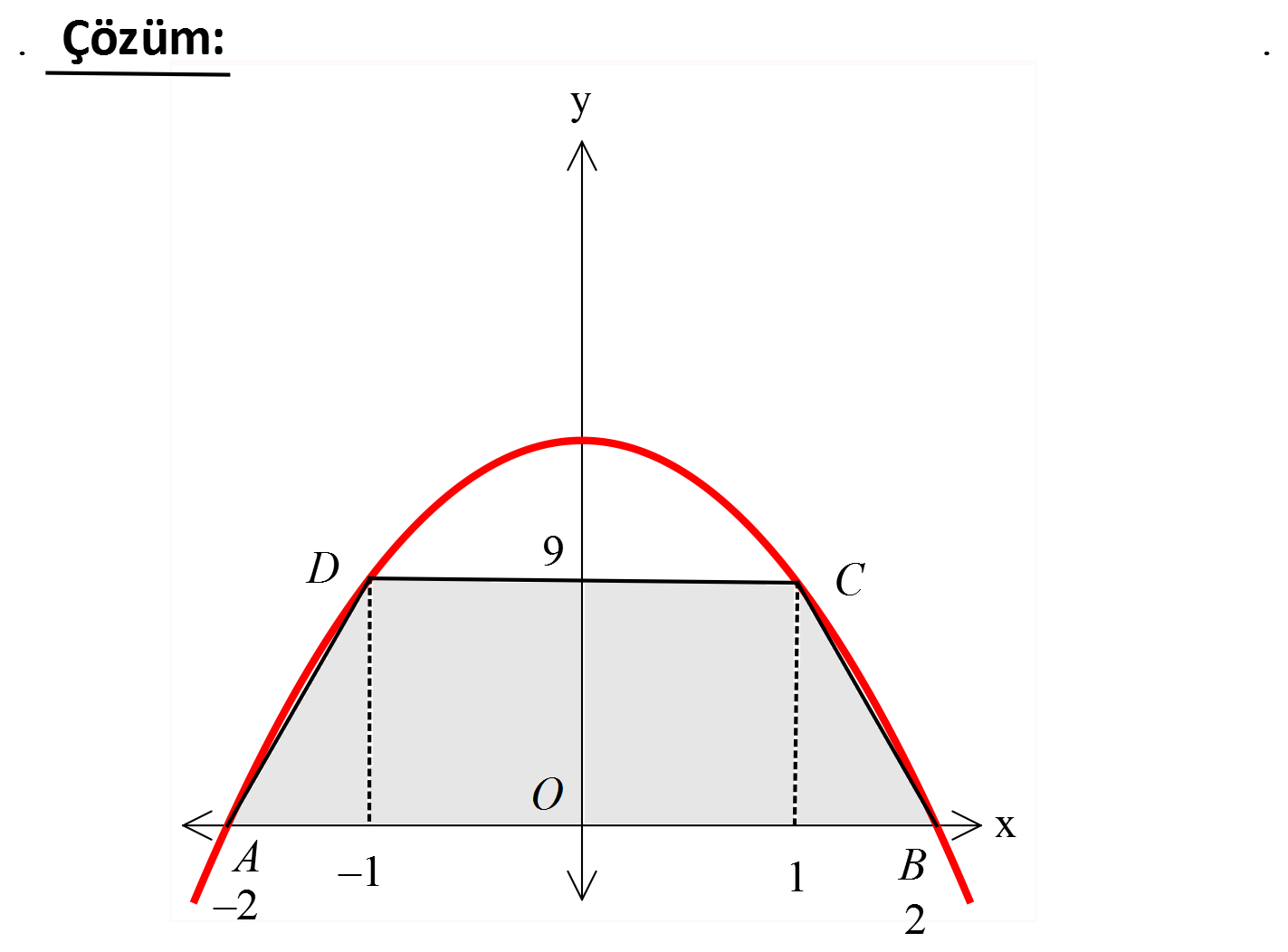
www.matematikkolay.net 2 2 Tepe noktası y ekseni üzerinde olan y ax a 9 x 12 parabolü ve yüksekliği 9 br olan ABCD yamuğuna gö 2 re, A ABCD kaç br dir? A) 21 B) 24 C) 27 D) 30 E) 33 www.matematikkolay.net 2 2 0 2 2 Tepe noktası y ekseni üzerinde ise b 0 dır. y ax a 9 x 12 a 9 0 a 9 a 3 tür. Parabo 2 2 2 2 lün kolları aşağı yönlü olduğundan a negatif olmalıdır. a 3 tür. y 3x 12 parabolünü elde ettik. x eksenini nerde keser bulalım. 0 3x 12 12 3x 4 x 2 2 x 2 dir. AB 2 2 4 birimdir. D ile C noktalarının apsislerini bulalım. y 9 olan noktalar; 9 3x 12 3 3x x 1 dir. DC 1 1 2 birimdir. 4 2 Yamuğun Alanı 9 27 2 2 br buluruz. 76
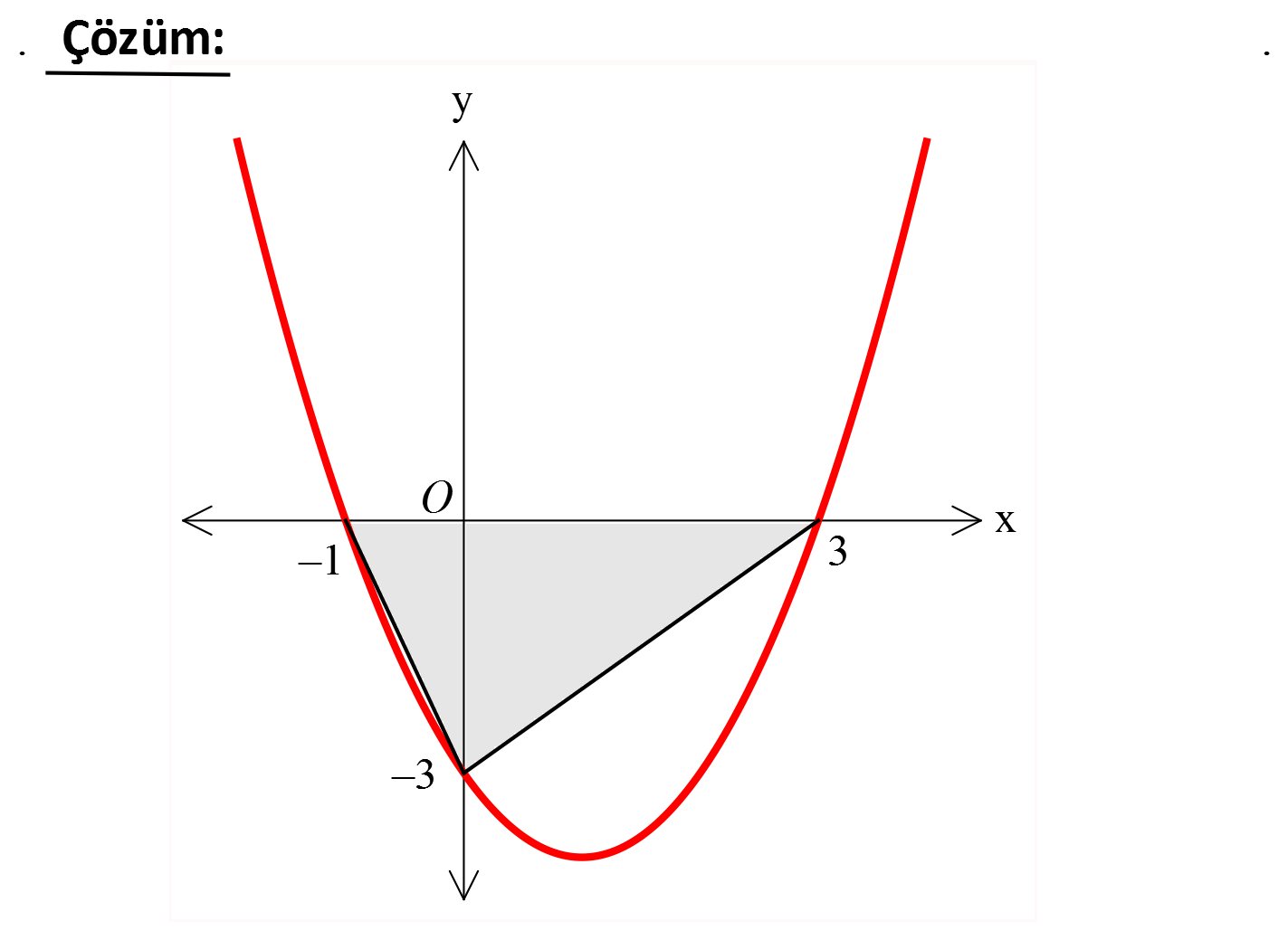
2 f x x 2x 3 fonksiyonunun eksenleri kestiği noktaları köşe kabul eden üçgenin alanı kaç birim karedir? A) 4 B) 5 C) 6 D) 7 E) 8 www.matematikkolay.net 2 0 0 2 Eksenleri kesen noktaları bulalım. x 0 için y x 2x 3 3 tür. 0, 3 noktası y 0 için 0 x 2x 3 0 x 3 x 1 x 3 ve x 1 dir. 3, 0 ve 1,0 noktaları Bu üç nokta ile çizilen üçgenin tabanı; 3 1 4 birimdir. Yüksekliği 3 birimdir. 4. Üçgenin Alanı 2 3 6 br buluruz. 2 77
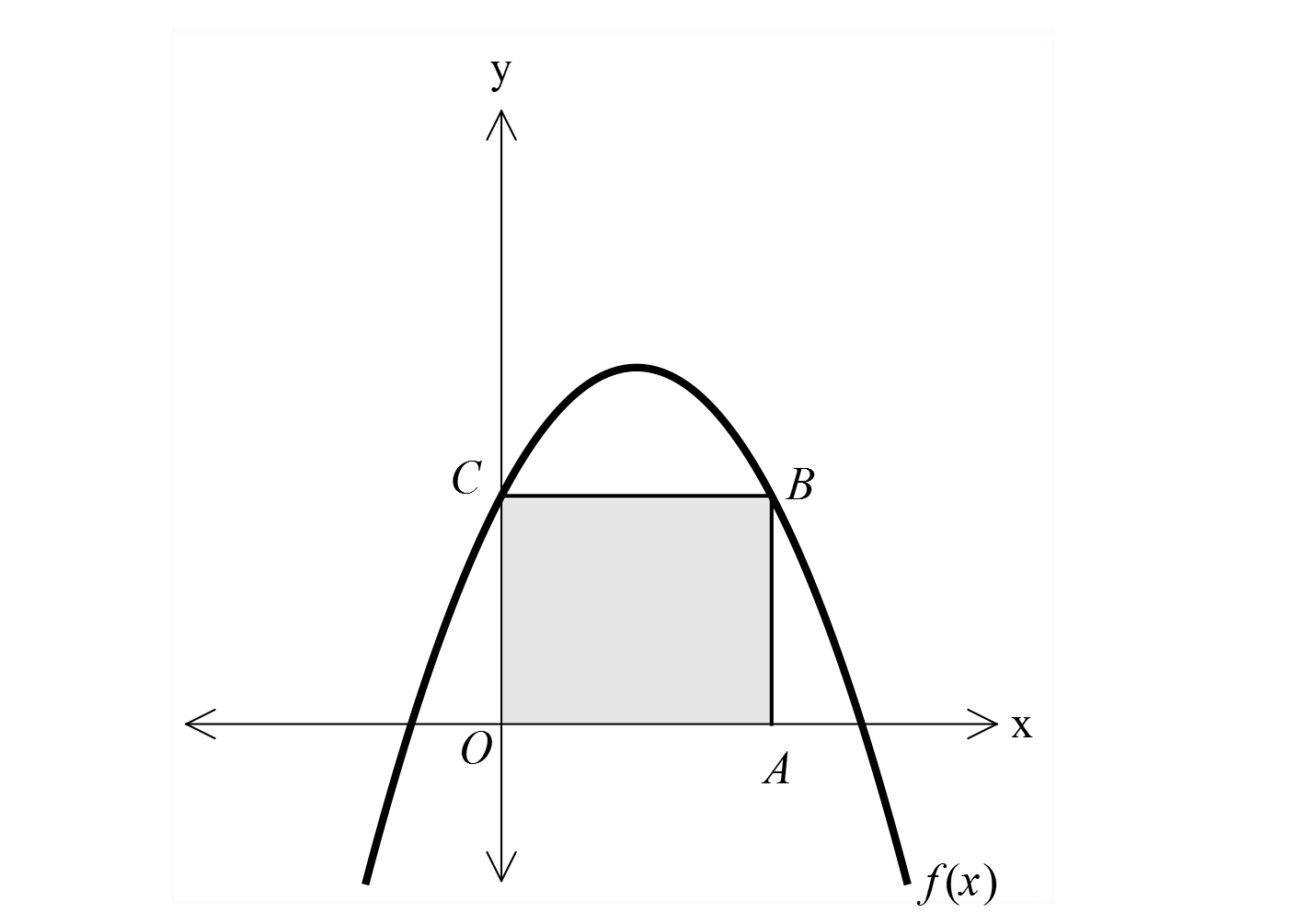
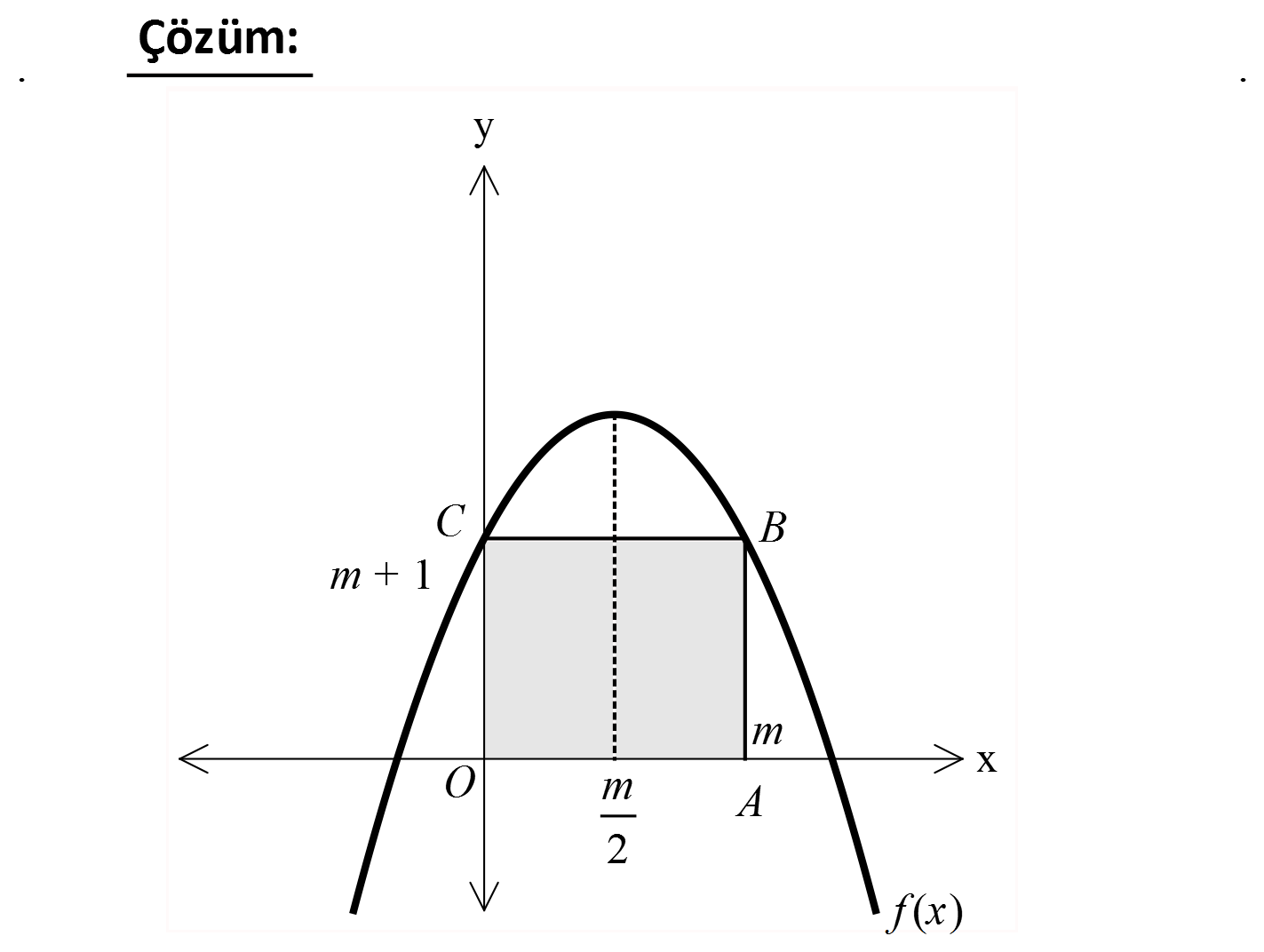
www.matematikkolay.net 2 2 Şekilde grafik f x x mx m 1 fonksiyonuna aittir. A OABC 12 br ise Çevre(OABC) kaç br dir? A) 14 B) 1 3 C) 12 D) 11 E) 10 www.matematikkolay.net 2 0 0 C noktasının ordinatını bulalım. x 0 için f x x mx m 1 m 1 dir. b Parabolün tepe noktası r 2 4 3 m m dir. 2a 2 2 m O ile A noktasının ortası ise, 2 A noktası m’dedir. A OABC 12 br ise m 1 m 12 m 3 tür. Ç OABC 2 m 1 m 2 2m 1 4m 2 4.3 2 12 2 14 buluruz. 82
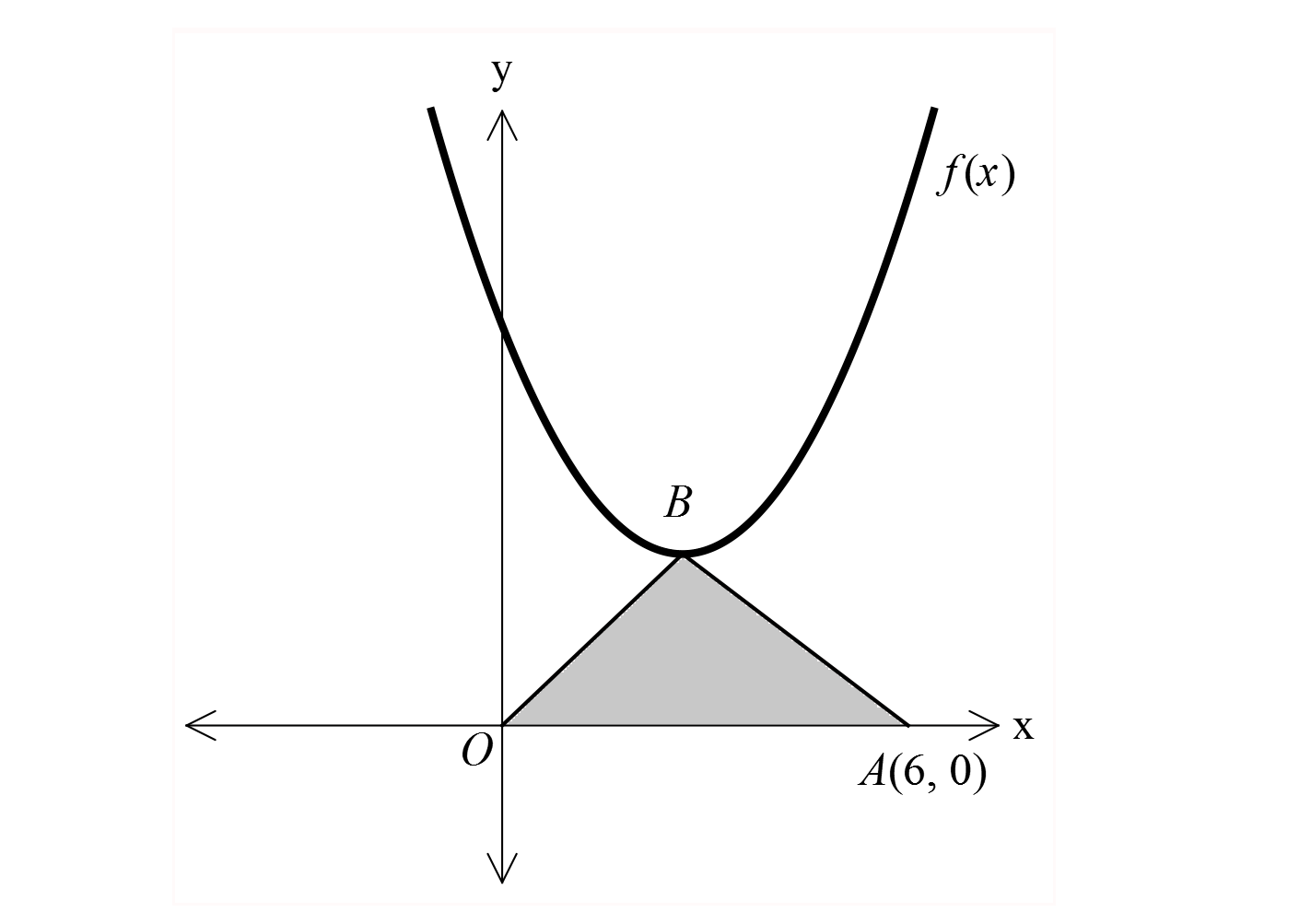
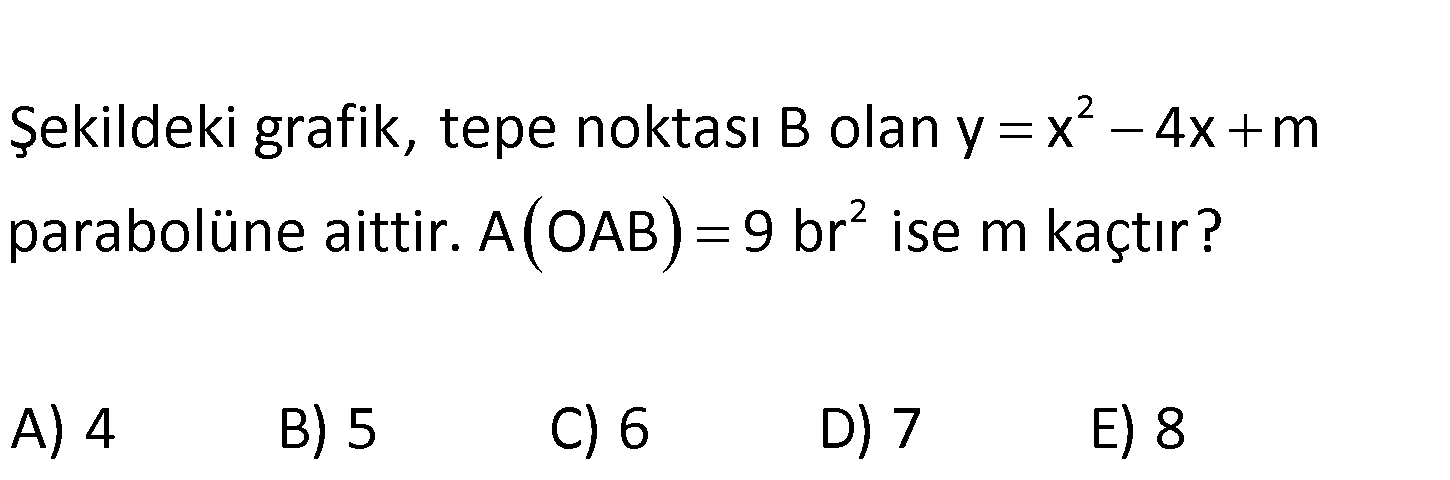
www.matematikkolay.net 2 2 Şekildeki grafik, tepe noktası B olan y x 4x m parabolüne aittir. A OAB 9 br ise m kaçtır? A) 4 B) 5 C) 6 D) 7 E) 8 www.matematikkolay.net 2 2 3 2 2 b 4 Parabolün tepe noktası r 2 dir. 2a 2 A OAB 9 br ise 6.k 9 6k 18 k 3 tür. 2 Tepe noktası r,k 2,3 noktası parabolün denklemini sağlamalıdır. y x 4x m 3 4 8 m 3 4 m 7 m dir. Cevap: 7 83
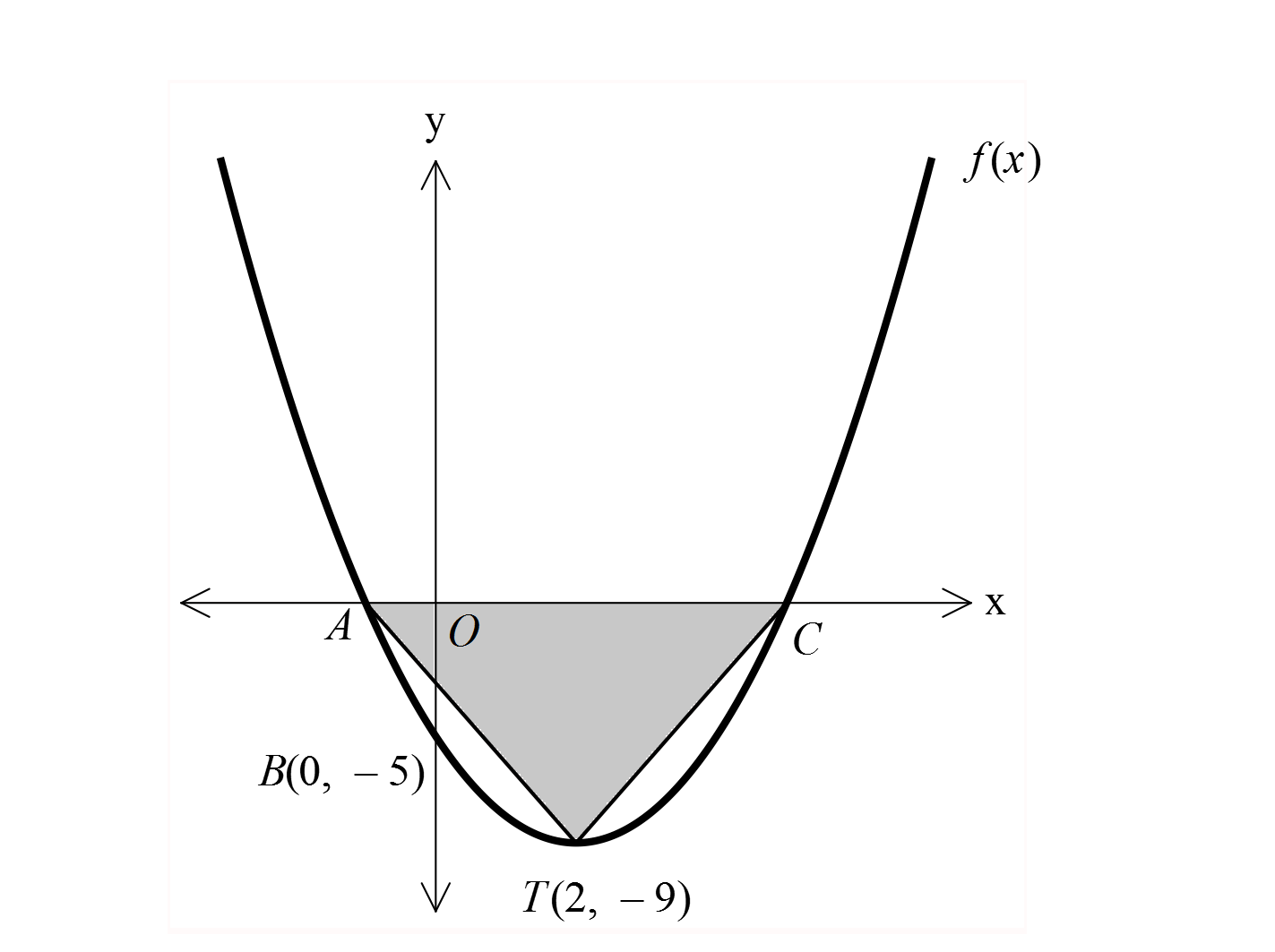
www.matematikkolay.net 2 Şekilde y f x parabolünün grafiği verilmiştir. Buna göre, ATC üçgeninin alanı kaç br dir? A) 23 B) 24 C) 25 D) 26 E) 27 2 2 Tepe noktası T r,k olan parabolün denklemi y a x r k şeklindedir. Buna göre; y a x 2 9 ya : zab Çözüm 2 2 2 2 2 3 veya 3 iliriz. 0, 5 noktası da parabolün bir noktası ise, 5 a 0 2 9 4 a 2 4 4a a 1 dir. Buna göre; y x 2 9 parabolün denklemidir. x eksenini kesen noktaları bulalım. 0 x 2 9 9 x 2 2 x 5 veya x 1 dir. AC 5 1 6 dır. 06.Eyl A ATC 27 br buluruz. 2 84
www.matematikkolay.net 2 Şekilde y x 4 parabolünün grafiği verilmiştir. ABCD eşkenar dörtgen olduğuna göre, C noktasını n koo rdinatları toplamı kaçtır? A) 24 B) 28 C) 32 D) 36 E) 40 2 y (x 4) x 4 için A noktasını bulabiliriz. A(4,0) x 0 için D noktasını bulabiliriz. : D(0, Çözüm 16) B noktasının da ordinatı, D ile aynıdır 16 B’nin apsisi ile D’nin apsisinin toplamının yarısı tepe noktasının apsisine eşit olduğundan ; x 0 4 x 8 dir. B(8,16) 2 C köşesininin apsisi; karşılıklı no ktaların apsisleri toplamı birbirine eşit olmalıdır. x 4 0 8 x 4 tür. Ordinatlar da aynı şekilde; y 0 16 16 y 32 dir. Buna göre; x y 4 32 36 buluruz. 30

