Soru Sor sayfası kullanılarak Parabol konusu altında Parabolün eksenleri kestiği noktalar ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU


5.SORU
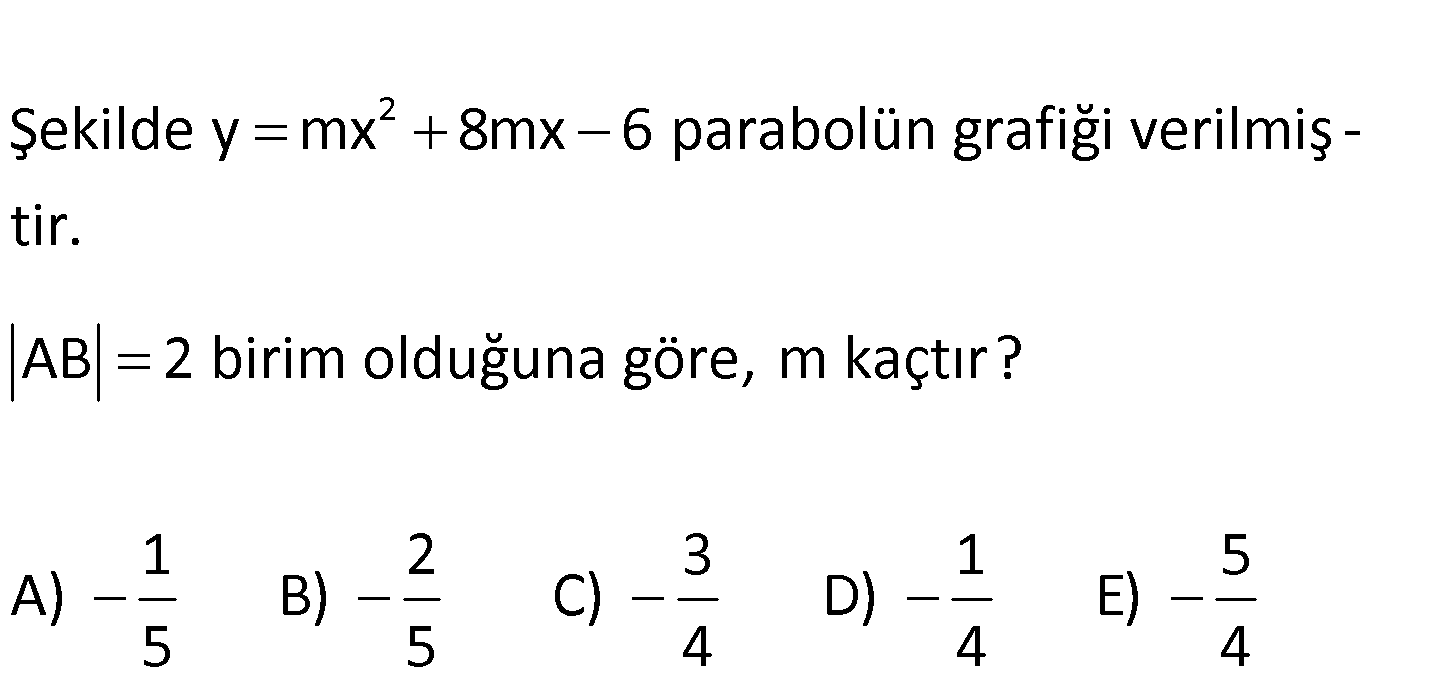

6.SORU


7.SORU

8.SORU


9.SORU

10.SORU


11.SORU
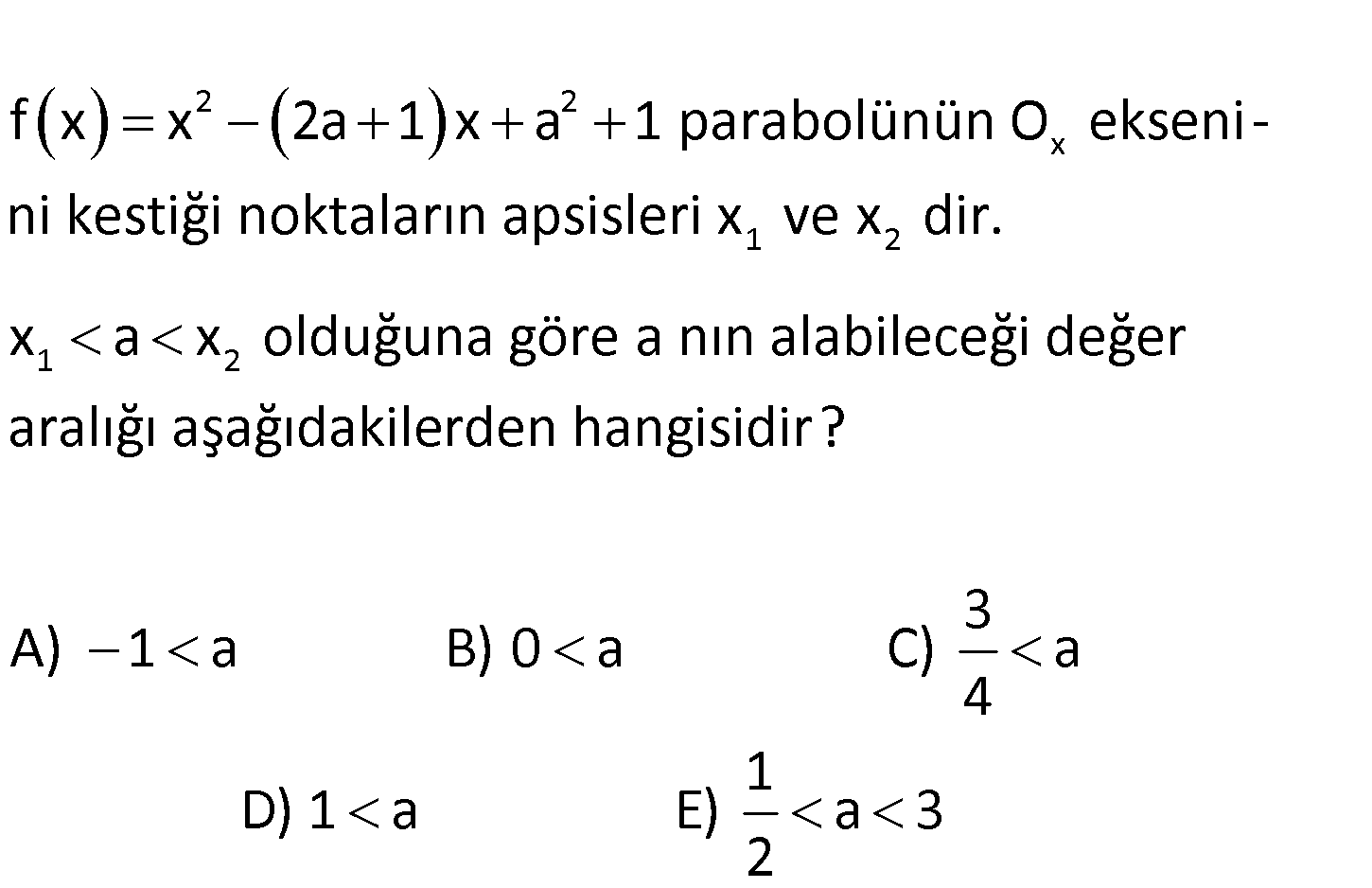
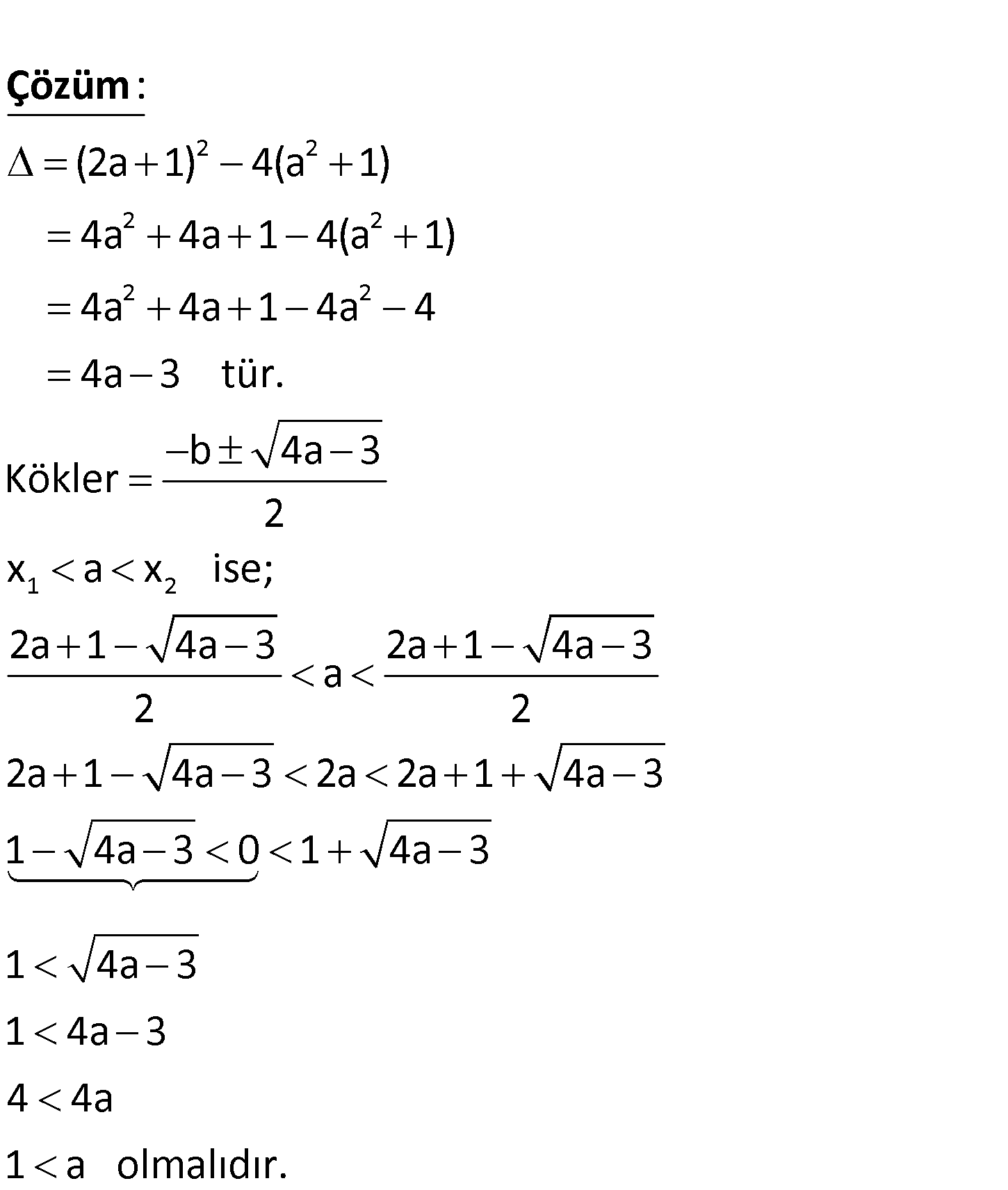
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 f x x mx m 1 parabolü x eksenini A ve B noktalarında kesmektedir. AB 3 br olduğuna göre, m say ı ıs nı n alabileceği değerler çarpımı kaçtır? A) 17 B) 13 C)10 D) 10 E) 13 2 1 2 2 2 2 1 2 2 1 1 2 x x 3 kare alalım. x x 9 (a b) (a b) 4ab x x 4x x 9 : m Çözüm 2 2 2 4(m 1) 9 m 4m 4 9 m 4m 13 0 13 Kökler çarpımı 13 buluruz. 1 www.matematikkolay.net 28
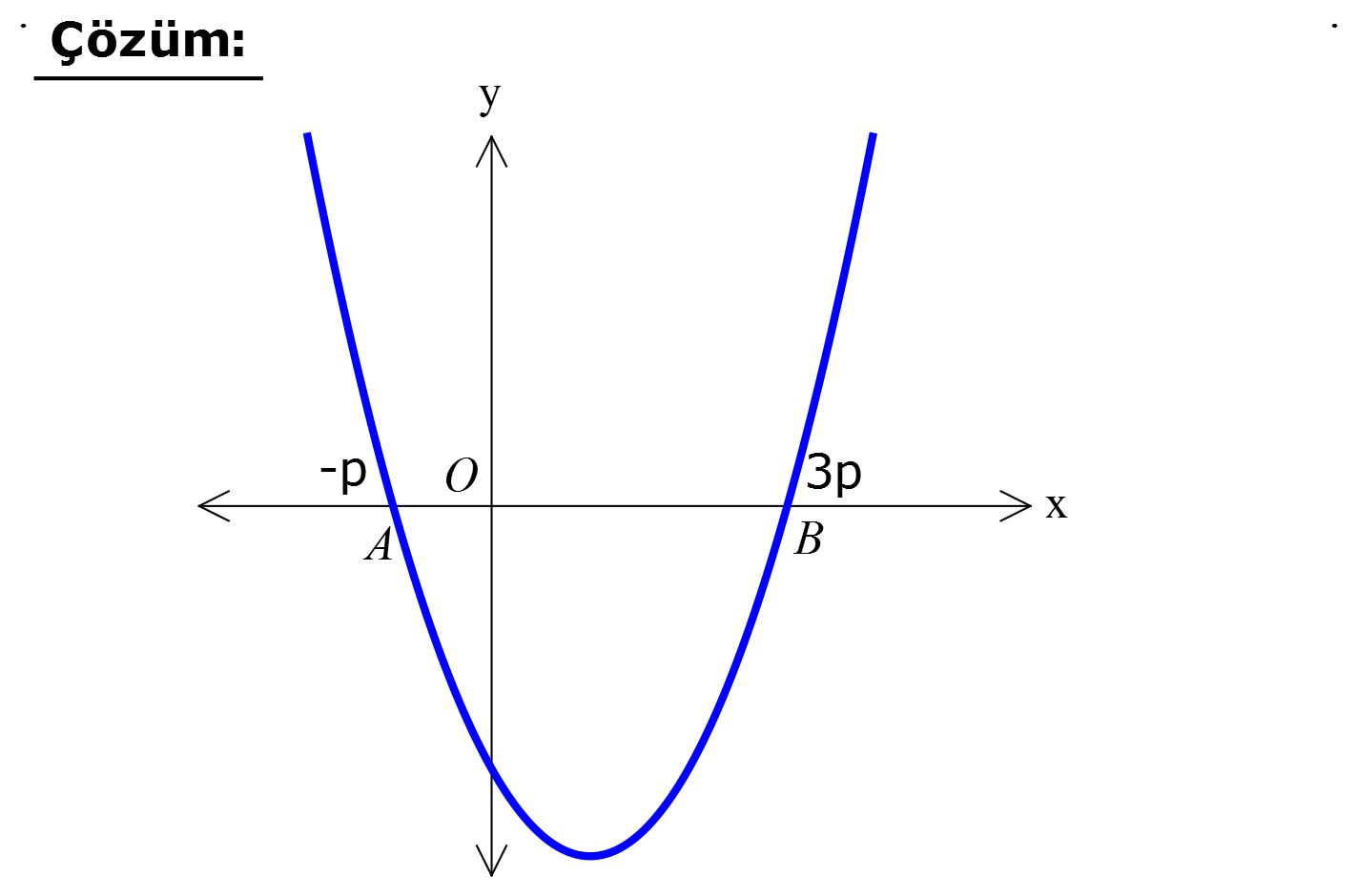
www.matematikkolay.net 2 Yukardaki şekilde, y x 4x k fonksiyonunun grafiği verilmiştir. OB 3 OA olduğuna göre, k kaçtır? A ) 4 B) 6 C) 8 D) 10 E) 12 www.matematikkolay.net A noktasına – p, B noktasına da 3p diyebiliriz. Bu ikisinin ortası r değerine eşittir. 4 r 2 di 2 r. p 3p 2 p 2 dir. 2 Buna göre; A noktası 2, B noktası da 6 dır. Kökler çarpımı ( 2).6 12 ise; k 12 k 12 dir. 1 31
2 m bir tamsayı olmak üzere, y x mx m parabolü x eksenini A ve B noktalarında kestiğine göre, AB uzunluğu en az kaç birim olabil A) 4 3 B) 3 5 C)2 2 D) 5 E) 3 ir? 2 y x mx m eksenleri kestiği noktalar A ve B ise b m A B m dir. a 1 c m A.B m dir. a 1 AB A B dır. A : Çözüm 2 2 2 2 2 2 2 B 4A.B A B dir. A B A B 4.A.B A B ( m) 4.m A B m 4m ifadesinini minimum değeri için kökün içi minimum ve pozitif olmalı. A B m 4m 4 4 4 ekle 4 çıkar A B m 2 4 m bir tam sayı olduğuna gör e, m 5 ya da 1 olmalı ki içerisi en küçük bir pozitif sayı olsun. A B 9 4 5 bulunur. 33
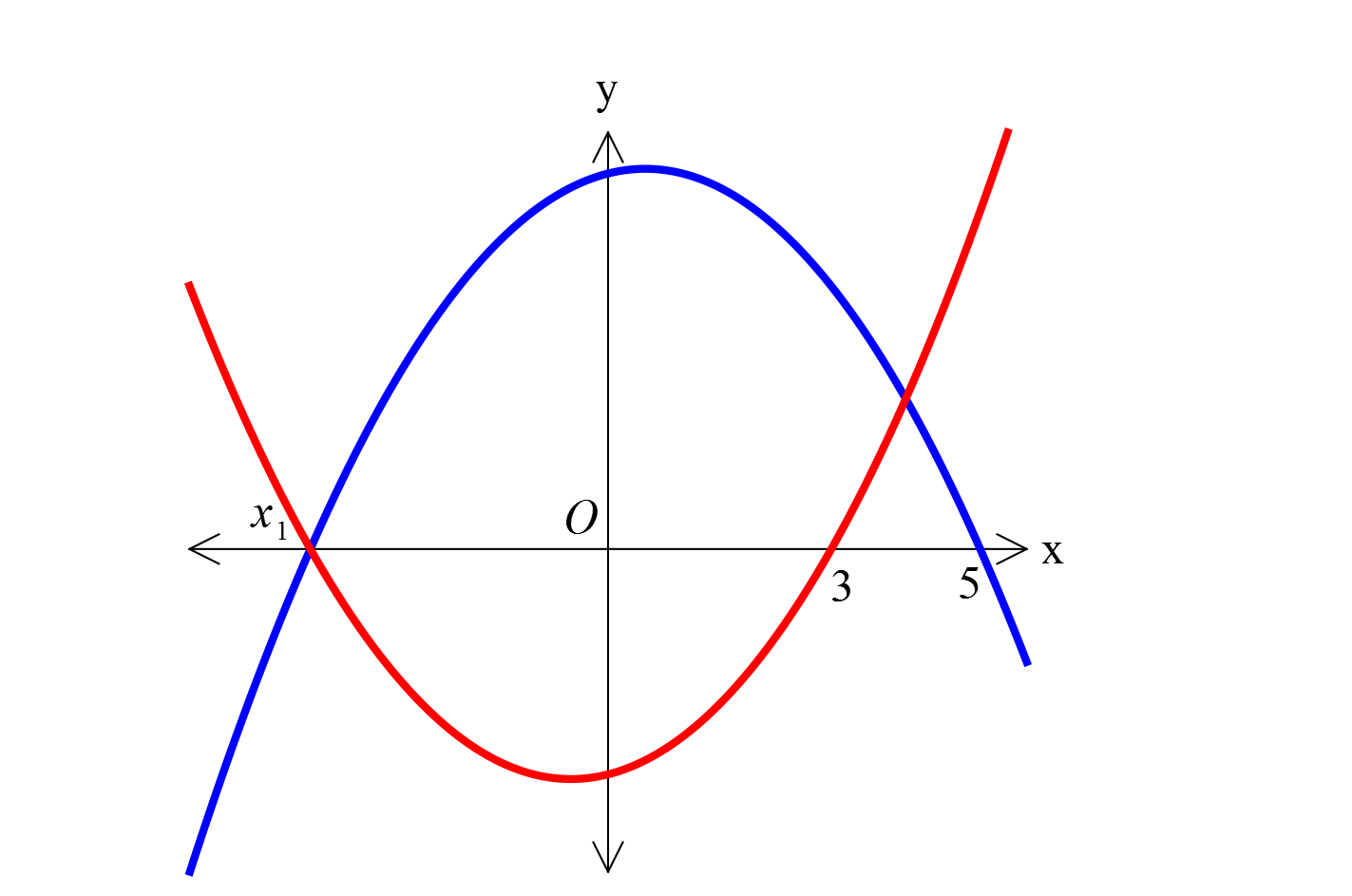
www.matematikkolay.net 2 1 2 Denklemi y x ax b olan parabol x , 0 ve 3, 0 noktalarından geç – mektedir. Denklemi y x 1 x c olan parabol x , 0 ve 5, 0 noktalarından geçtiğine göre, a 2b c top – lamı kaçtır? A) 3 B) 3 C) 1 D) 1 E) 8 2 2 2 (5, 0) noktası y x x c parabolünü sağlar. 0 5 5 c 0 20 c c 20 dir. y x x : 20 is Çözüm 1 1 2 1 e kökler toplamı 1 dir. 1 x 5 1 x 4 tür. y x ax b parabolünün kökleri 4 ve 3 ise; Kökler toplamı a 4 3 a 1 a 1 Kökler çarpımı b 12 dir. a 2b c 1 2( 12) 20 1 24 20 3 tür. 42
2 Şekilde y mx 8mx 6 parabolün grafiği verilmiş – tir. AB 2 birim olduğuna göre, m kaçtır? 1 2 A) B) 5 5 3 1 5 C) D) E) 4 4 4 www.matematikkolay.net 1 2 1 2 2 1 2 x ve x parabolün kökleri olsun. AB x x 2 y mx 8mx 6 b 8m x x 8 dir. a m İki denklemi alt : Çözüm 1 2 1 2 1 1 2 alta toplayalım. x x 8 x x 2 2x 6 x 3 tür. Bu değeri denklemde yazıp 0’a eşitlersek m değerini buluruz. m. 3 8m 3 6 0 9m 24m 6 15m 6 6 2 m bulunur. 15 5 46
2 2 Tepe noktası y ekseni üzerinde olan f x mx m 4 x 3m 2 parabolünün x eksenini kestiği noktalar 1 2 1 2 ın apsisleri x ve x olduğuna göre, x x kaç olabilir? 4 3 A) 5 B) C) 4 D) 1 E) 3 4 www.matematikkolay.net 2 2 Tepe noktasının apisisi 0 dır. b m 4 r 0 olmalıdır. a m m 4 0 m 2 : Çözüm 2 2 2 2 2 veya 2 dir. m 2 ise y 2x 4 olur. 2x 4 0 x 2 ve 2 dir. Farkları 2 2 olur. m 2 ise y 2x 8 olur. 2x 8 0 x 4 x 2 veya 2 dir. Farkları 2 2 4 buluruz. Cevap: 4 55
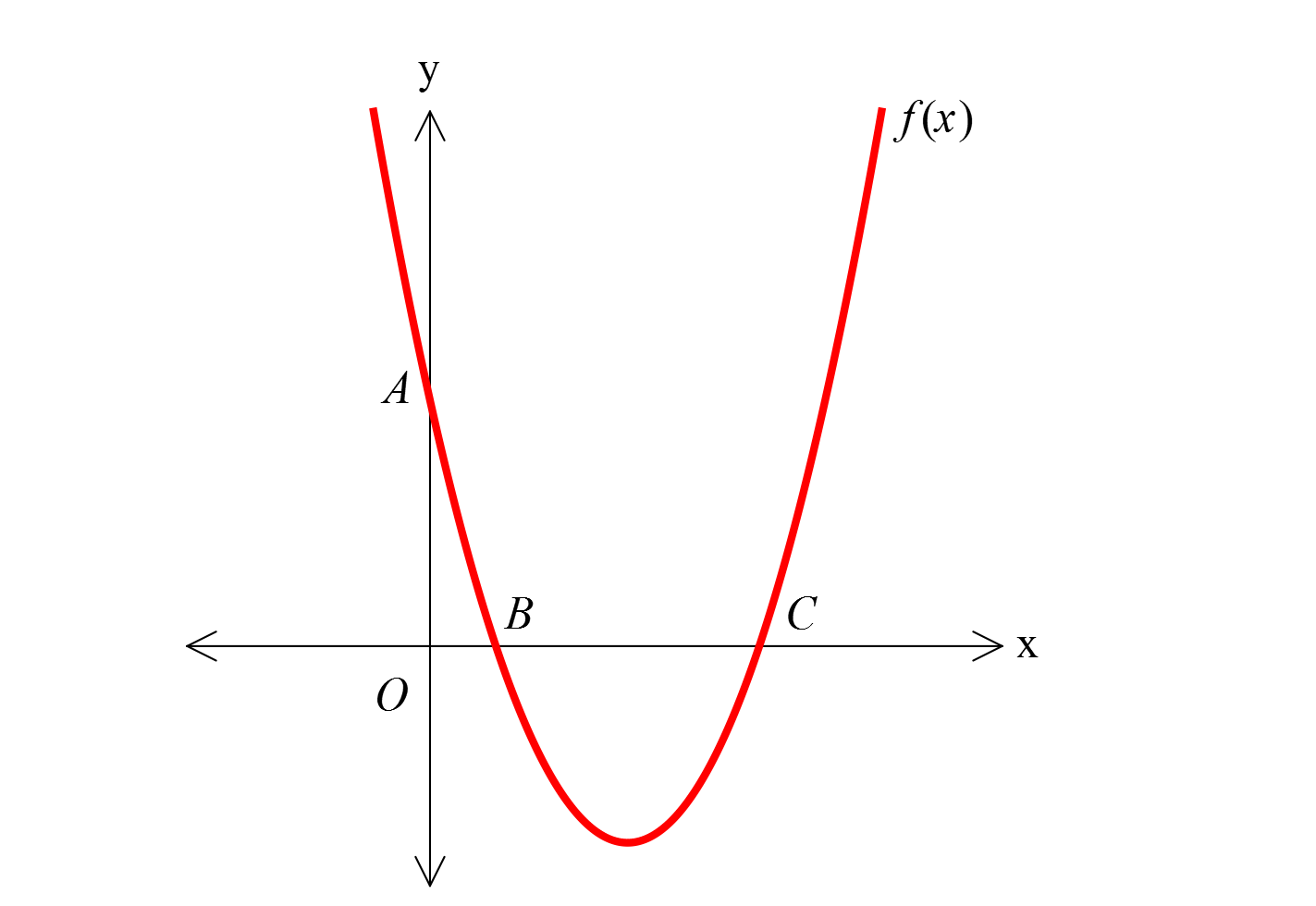
www.matematikkolay.net 2 Yukarıda f x x 6x k parabolünde OA OC olduğuna göre, f x in alabileceği en küçük değer kaçtır? A ) 1 B) 2 C) 3 D) 4 E) 6 www.matematikkolay.net x 0 için f(x) k dır. Yani A noktası 0, k noktasıdır. OA k ise OC k dır. Buna göre, : Çözüm 2 2 2 C noktası k, 0 noktasıdır. Bu nokta, denklemin bir köküdür. Yerine yazalım. k 6k k 0 k 5k 0 k k 5 0 k 5 tir. O halde parabolün denklemi f(x) x 6x 5 tir. Parabolün tepe noktasını bulalım. r 2 6 3 2 r 3 için f(3) 3 6.3 5 9 18 5 4 tür. Cevap: 4 65
2 f x x 4x 3 parabolünün e ksenleri kestiği nokt al ar ? 2 ( 1).( 3) Denklemi 0 yapan kökler, ekseni kesen noktalardır. x 4x 3 0 ( 1 : x Çözüm )(x 3) 0 x 1 veya x 3 tür. Ekseni kestiği noktalar (1,0) ve (3,0) dır. 23
2 2 2 y 2x 5x a b parabolünün Ox eksenini kestiği noktalar a ve b olduğuna göre, Oy eksenini kestiği n ok tanın ordi – natı kaçtır? 25 25 25 5 5 A) B) C) D) E) 8 4 2 4 2 www.matematikkolay.net 5 5 Kökler toplamı dir. 2 2 5 Demek ki a b dir. 2 Kökler çarpımı a.b dir. Denkleme : göre kökle Çözüm 2 2 2 2 2 2 2 2 2 2 2 2 a b r çarpımı dir. 2 Bu ikisini eşitleyelim. a b ab 2 2ab a b 0 a b 2ab 0 a b a b dir. O halde; 5 5 5 5 a b 2a a tür. b tür. 2 2 4 4 25 25 50 25 a b dir. 16 16 16 8 2 O halde; y 2x 5x 5 dir. 8 25 x 0 için y buluruz. 8 66
www.matematikkolay.net 2 2 f x ax bx c parabolü için f 5 0 f 3 0 olduğu bilinmektedir. Buna göre, I. b 4ac II. f 1 0 III. parabol x eksenini, apsisi 3, 5 aralığında olan en az bir noktada keser. yargılarından hangisi ya da hangileri ke sinlikle doğrudur? A) Yalnız I B) Yalnız II C) I ve II D) I ve III E) I, II ve III www.matematikkolay.net Bir parabolde 0 ise hiç kökü yoktur. x eksenini kesemez. 0 ise x eksenine teğettir. 0 : Çözüm ise 2 farklı kökü var dır. x eksenini 2 kere keser. Parabolün hem pozitif hem de negatif değerler aldığı yerler var dır. Bu parabolün de hem pozitif değerleri hem de negatif değerleri o 2 2 lduğu için 0 dır. b 4ac 0 b 4ac dir. I.öncül doğru f( 1)’in değeri pozitif mi negatif mi bilemeyiz. Ekseni kesen noktaları bilmemiz gerekir. Bu parabol x 3 için pozitif iken, x 5 iç in negatif ise x eksenini en az bir kere kesmiş olmalı ki negatif bölgeye geçiş yapsın III. öncül doğru Cevap: D 68
www.matematikkolay.net 2 2 x 1 2 1 2 f x x 2a 1 x a 1 parabolünün O ekseni – ni kestiği noktaların apsisleri x ve x dir. x a x olduğu na göre a nın alabileceği değer aralığı aşağıdakilerden hangisidir? 3 A) 1 a B) 0 a C) a 4 1 D) 1 a E) a 3 2 2 2 2 2 2 2 1 (2a 1) 4(a 1) 4a 4a 1 4(a 1) 4a 4a 1 4a 4 4a 3 tür. b 4a 3 Kökler 2 x a x : Çözüm 2 ise; 2a 1 4a 3 2a 1 4a 3 a 2 2 2a 1 4a 3 2a 2a 1 4a 3 1 4a 3 0 1 4a 3 1 4a 3 1 4a 3 4 4a 1 a olmalıdır. 21

