Soru Sor sayfası kullanılarak Parabol konusu altında Parabol ile kesişen noktalar ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
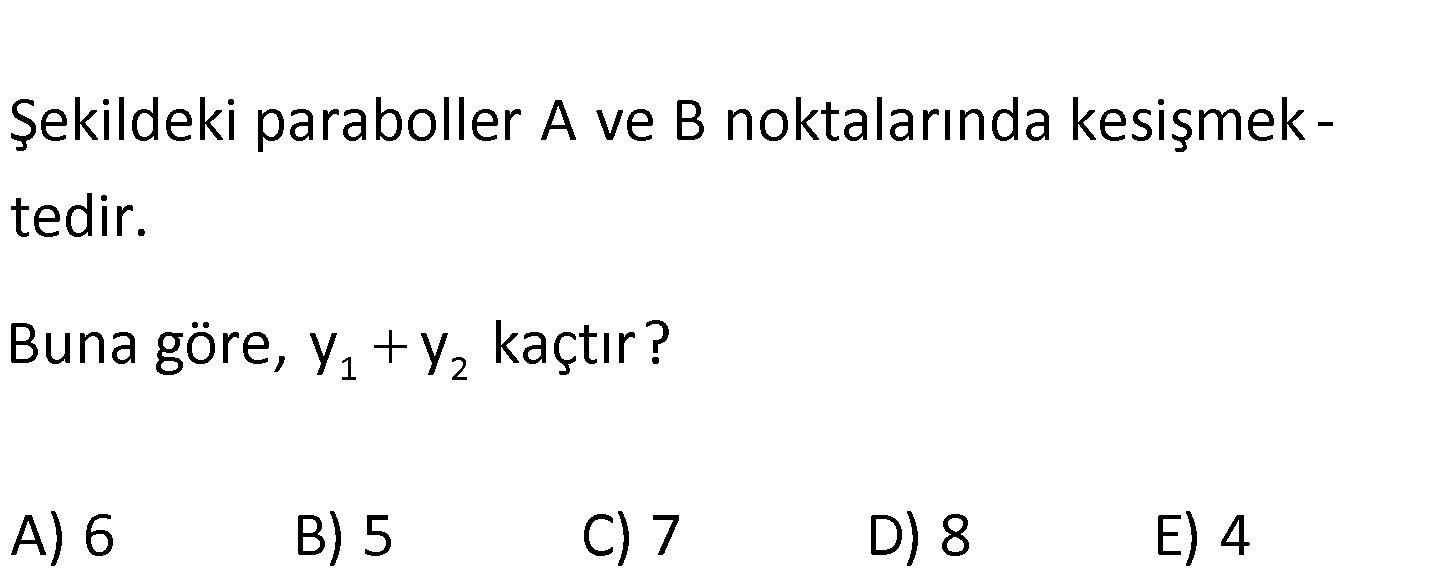
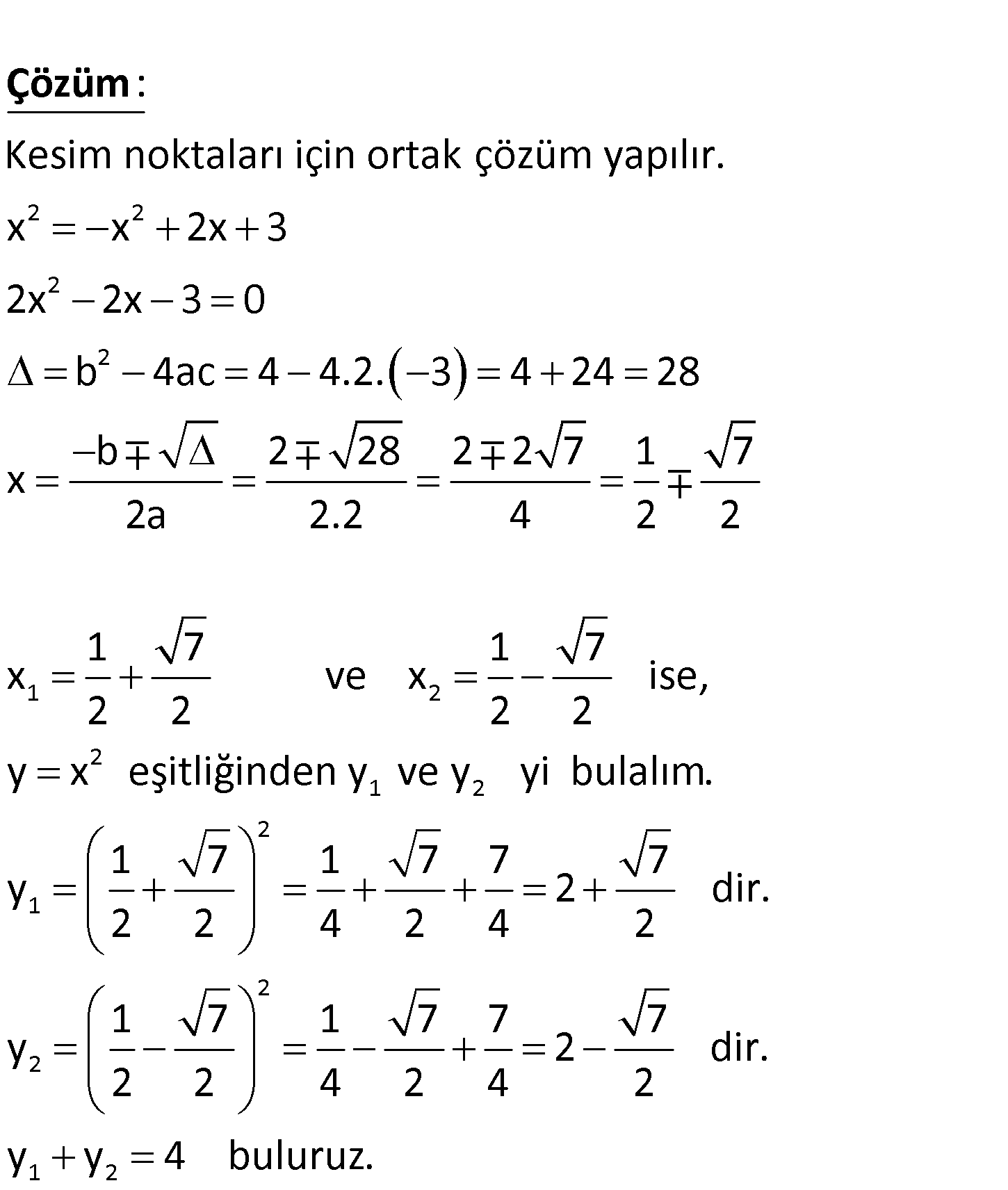
2.SORU


3.SORU


4.SORU


5.SORU


6.SORU
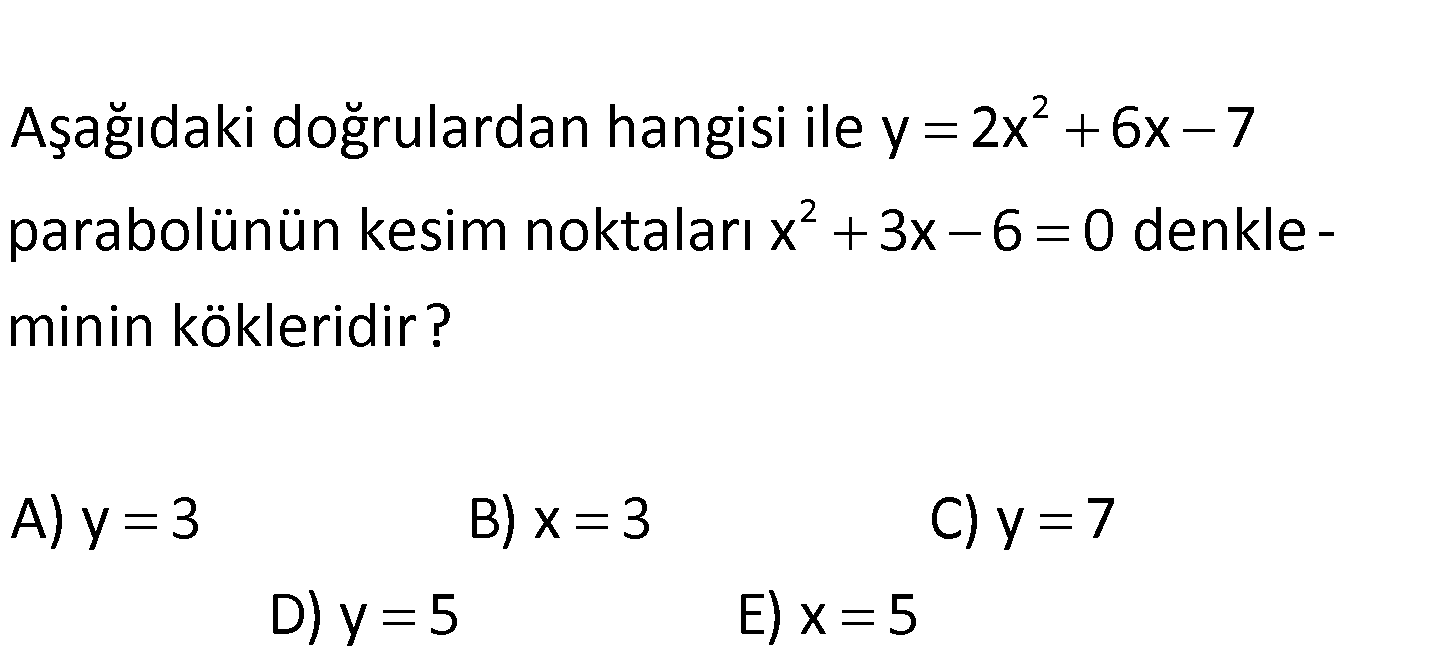

7.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
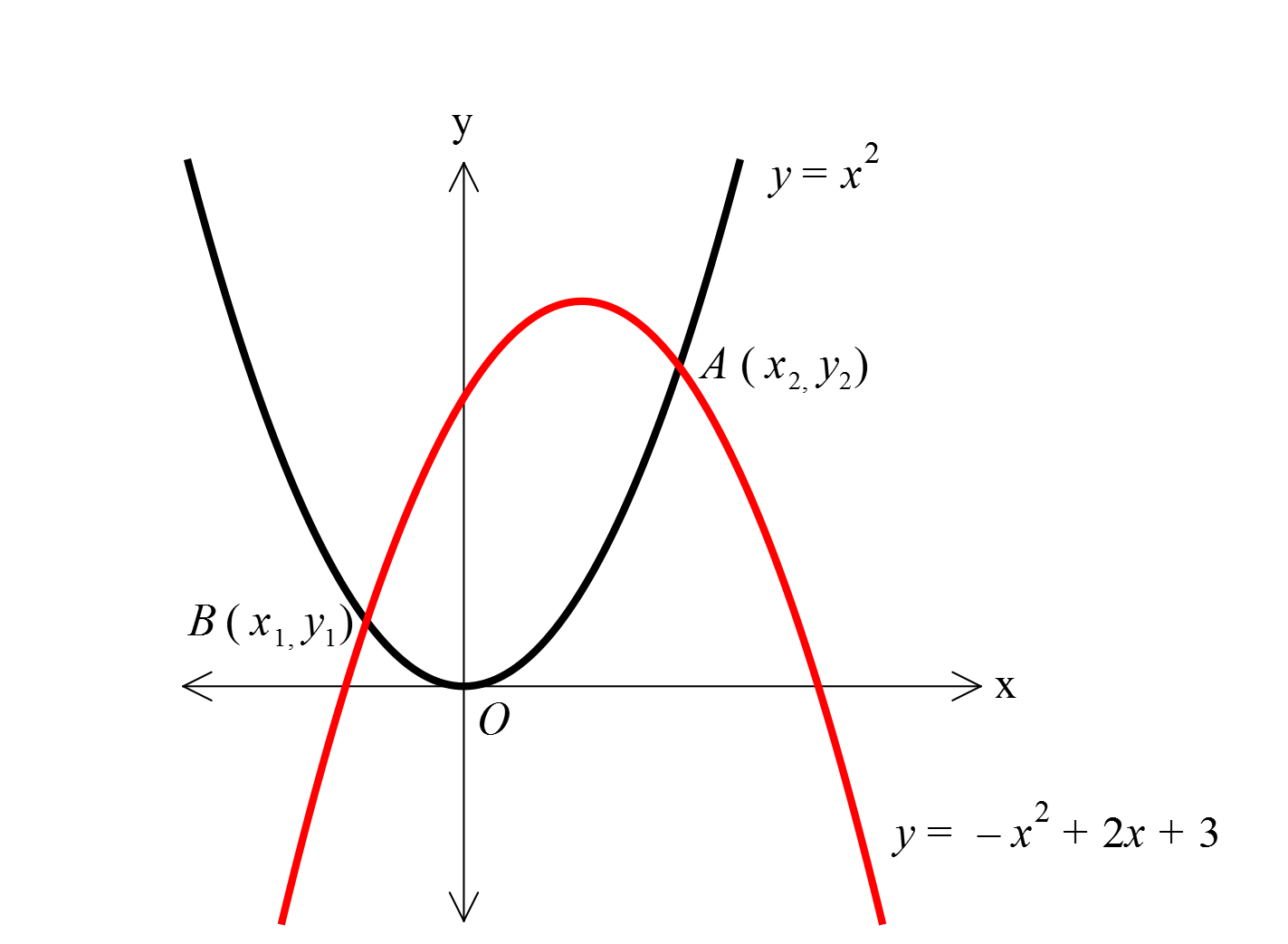
www.matematikkolay.net 1 2 Şekildeki paraboller A ve B noktalarında kesişmek – tedir. Buna göre, y y kaçtır? A) 6 B) 5 C) 7 D) 8 E) 4 www.matematikkolay.net 2 2 2 2 Kesim noktaları için ortak çözüm yapılır. x x 2x 3 2x 2x 3 0 b 4ac 4 4.2. 3 4 2 : 4 28 b x Çözüm 1 2 2 1 2 2 1 2 2 1 2 2 28 2 2 7 1 7 2a 2.2 4 2 2 1 7 1 7 x ve x ise, 2 2 2 2 y x eşitliğinden y ve y yi bulalım. 1 7 1 7 7 7 y 2 dir. 2 2 4 2 4 2 1 7 1 7 7 7 y 2 dir. 2 2 4 2 4 2 y y 4 buluruz. 86
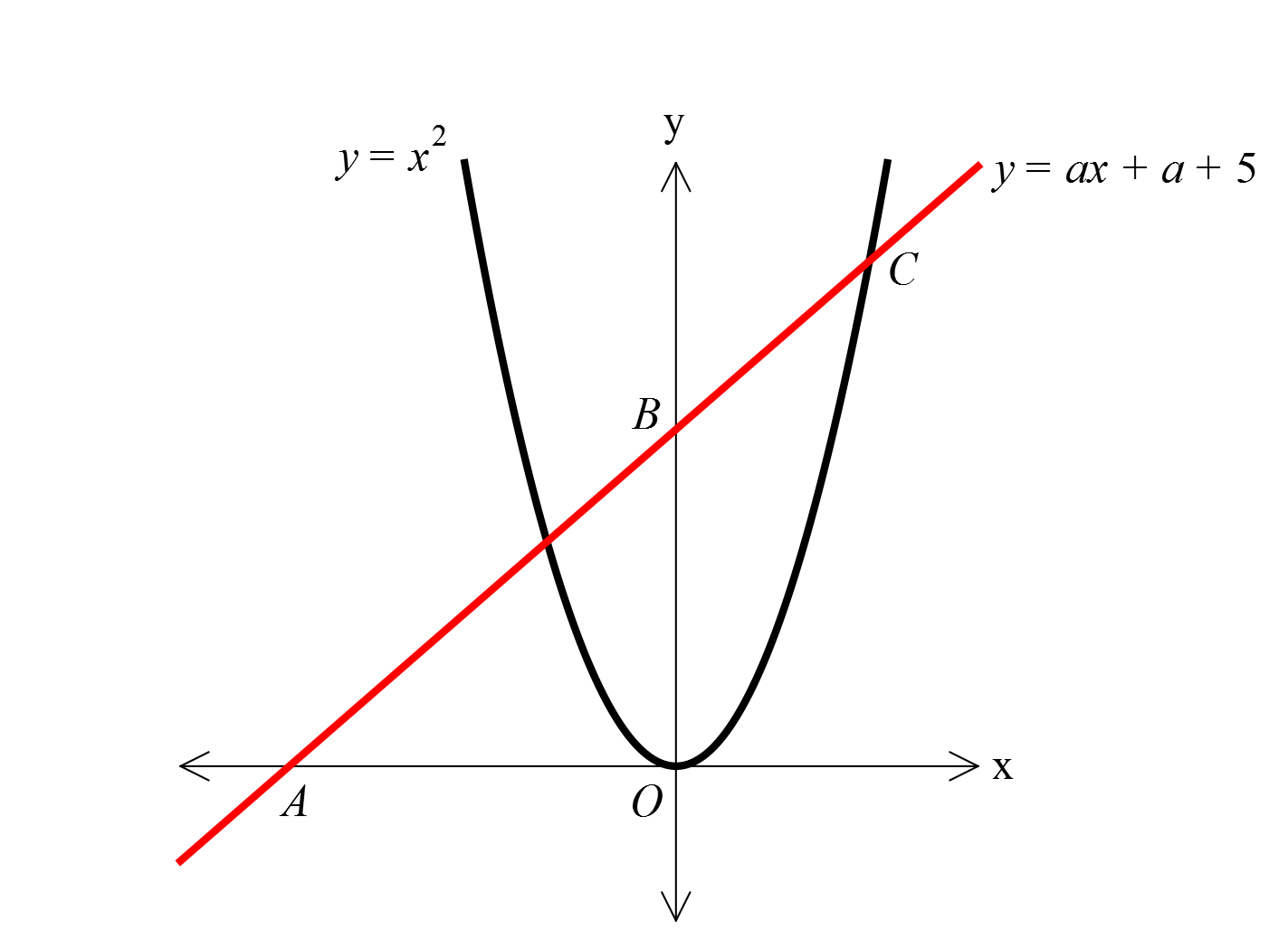
www.matematikkolay.net Şekildeki grafikte AO OB olduğuna göre, C noktasının ordinatı kaçtır? A) 4 B) 9 C) 16 D) 25 E) 36 y ax a 5 x 0 için y a 5 tir. B noktası 0,a 5 tir. AO OB ise A noktası a 5,0 : olmal Çözüm ıdır. x 5 a için y 0 ise, y ax a 5 y a a 5 a 5 a 5 a a 5 2 2 2 03.Şub 2 2 a 1 dir. y x 1 5 y x 6 doğrusu ile y x nerde kesişir bulalım. x 6 x 0 x x 6 x 3 x 2 x 3 te C noktası y x idi. y 3 9 buluruz.
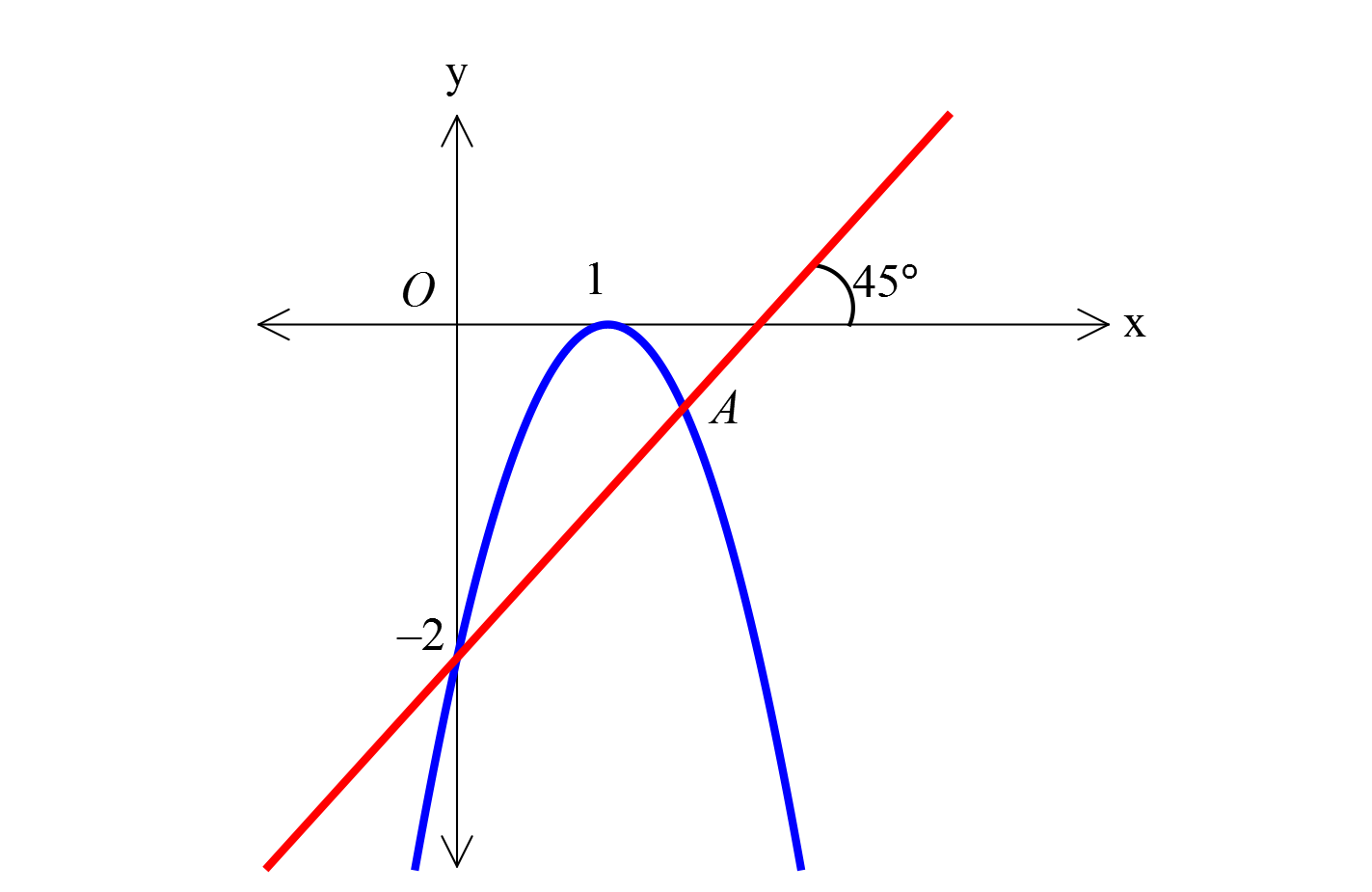
www.matematikkolay.net Şekilde parabol x eksenine x 1 noktasında teğet ve y eksenini y 2 noktasında kesmektedir. Verilenle re göre, A noktasının ordinatı kaçtır? 1 1 4 5 A) B) C) D) 2 E) 4 2 3 2 www.matematikkolay.net 2 Parabolün denklemi: y a x 1 şeklindedir. 0, 2 noktasını kullanarak a’ yı bula ı a : l m. 2 Çözüm 2 2 0 1 2 a a 2 dir. y 2 x 1 olur. Doğrunun eğimi: tan45 1 dir. 0, 2 noktasından geçen ve eğimi 1 olan doğru; y 2 1 x 0 y 2 x y x 2 dir. Kesiştikleri noktaları bulmak için iki denklem 2 2 2 i birbirine eşitleyelim. 2 x 1 x 2 2 x 2x 1 x 2 2x 4x 2 x 2 2 2x 3x 0 3 x 2x 3 0 x 0 veya x dir. 2 3 3 1 x için y x 2 2 buluruz. 2 2 2 53
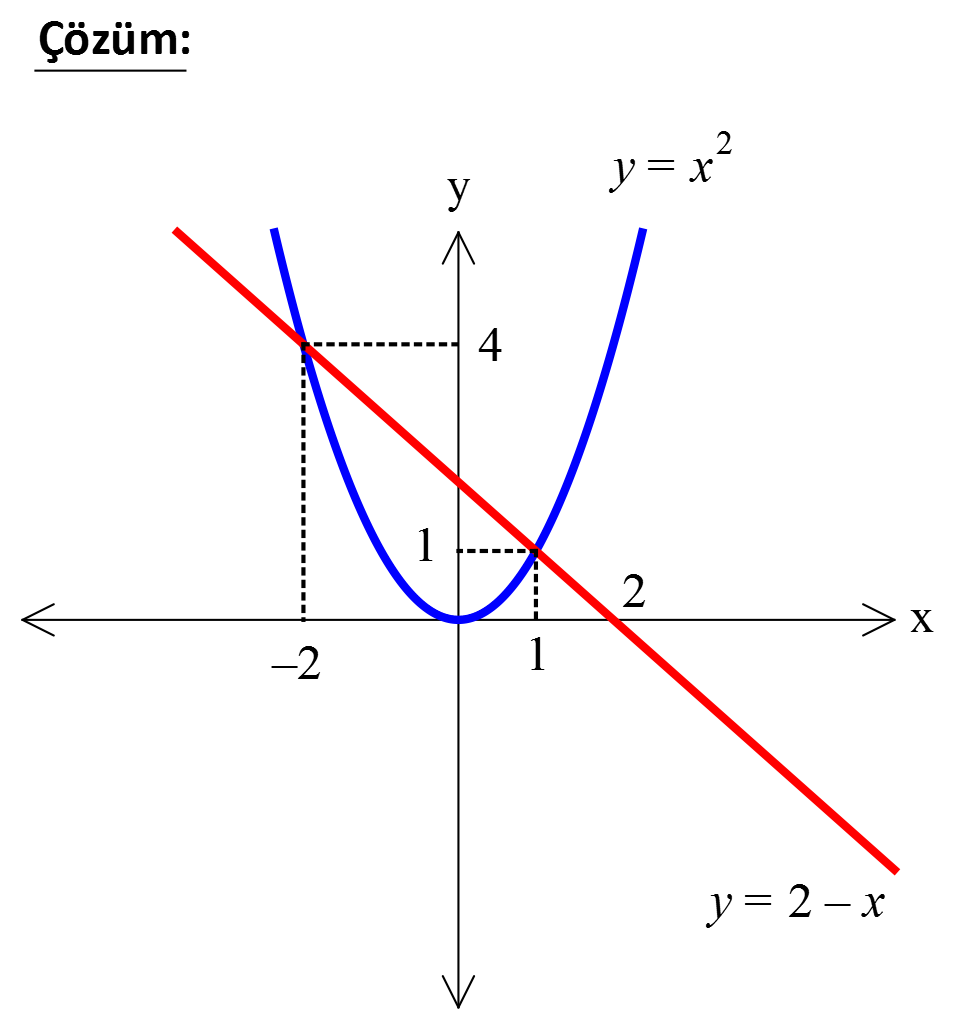
2 y x parabolü ile y 2 x doğrusu arasında kalan sınırlı bölg enin sınırları üzerindeki x, y noktaları 2 2 için x y ifadesinin alabileceği en büyük değer kaçtır? A) 25 B) 20 C) 17 D) 13 E) 10 2011 LYS 1 www.matematikkolay.net 2 2 2 y x ile y 2 x in kesiştiği noktalarını bulalım. Bu noktalardan biri x y için en büyük değeri 2 2 2 2 verir. x 2 x x x 2 0 (x 2)(x 1) 0 x 1 ve x 2 Buna göre Kesişim noktaları (1,1) ve ( 2,4) ( 2,4) noktasında x y 4 16 20 en büyük değeri alır. Doğru Cevap : B şıkkı 2
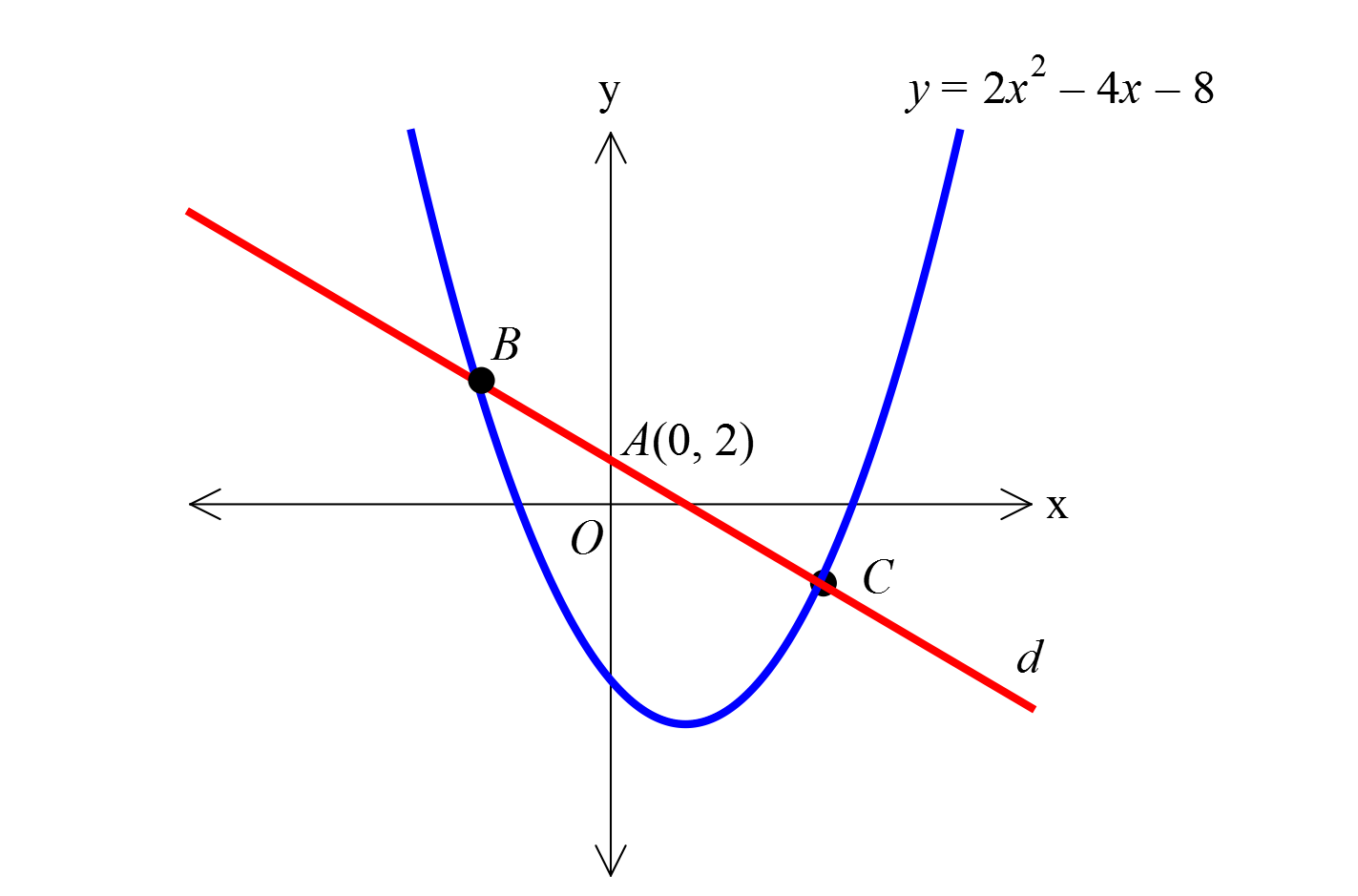
www.matematikkolay.net 2 Şekilde y 2x 4x 8 fonksiyonunun grafiği veril – miştir. A 0, 2 ve AB AC olduğuna göre, B ve C noktal arının apsislerinin çarpımı kaçtı A) 12 B) 10 C) 8 D) 5 E) 4 r? 2 2 B ve C noktalarının apsisleri b ve c olsun. B(b, 2b 4b 8) C(c, 2c 4c 8) olur. A noktası, : Çözüm 2 2 2 2 0 2 2 2 2 2 0 bu iki nok tanın orta noktası olduğundan b c 0 dır. 2b 4b 8 2c 4c 8 4 tür. Bu denklemi çözelim. 2(b c ) 4(b c) 16 4 2(b c ) 20 b c 10 (b c) 2bc 10 2bc 10 bc 5 buluruz. 35
2 2 Aşağıdaki doğrulardan hangisi ile y 2x 6x 7 parabolünün kesim noktaları x 3x 6 0 denkle – minin kök leridir? A) y 3 B) x 3 C) y 7 D) y 5 E) x 5 www.matematikkolay.net 2 y 2x 6x 7 doğrusu ile y a şeklinde bir doğrunun iki noktada kesişmesi lazımdır. Bu eşitl : Çözüm 2 2 2 2 ikten çıkacak kökler, aynı zamanda x 3x 6 denkleminin kökleri olabilsin. y a şeklinde bir doğruyu, parabole eşitlersek; 2x 6x 7 a 2x 6x 7 a 0 olur. Her tarafı 2′ ye bölelim. a 7 x 3x 0 o 2 2 lur. Bu denklem ile x 3x 6 0 denklemi aynı olmalıdır. a 7 6 olur. a 7 12 2 a 5 buluruz. y 5 doğrusu olmalıdır. 57
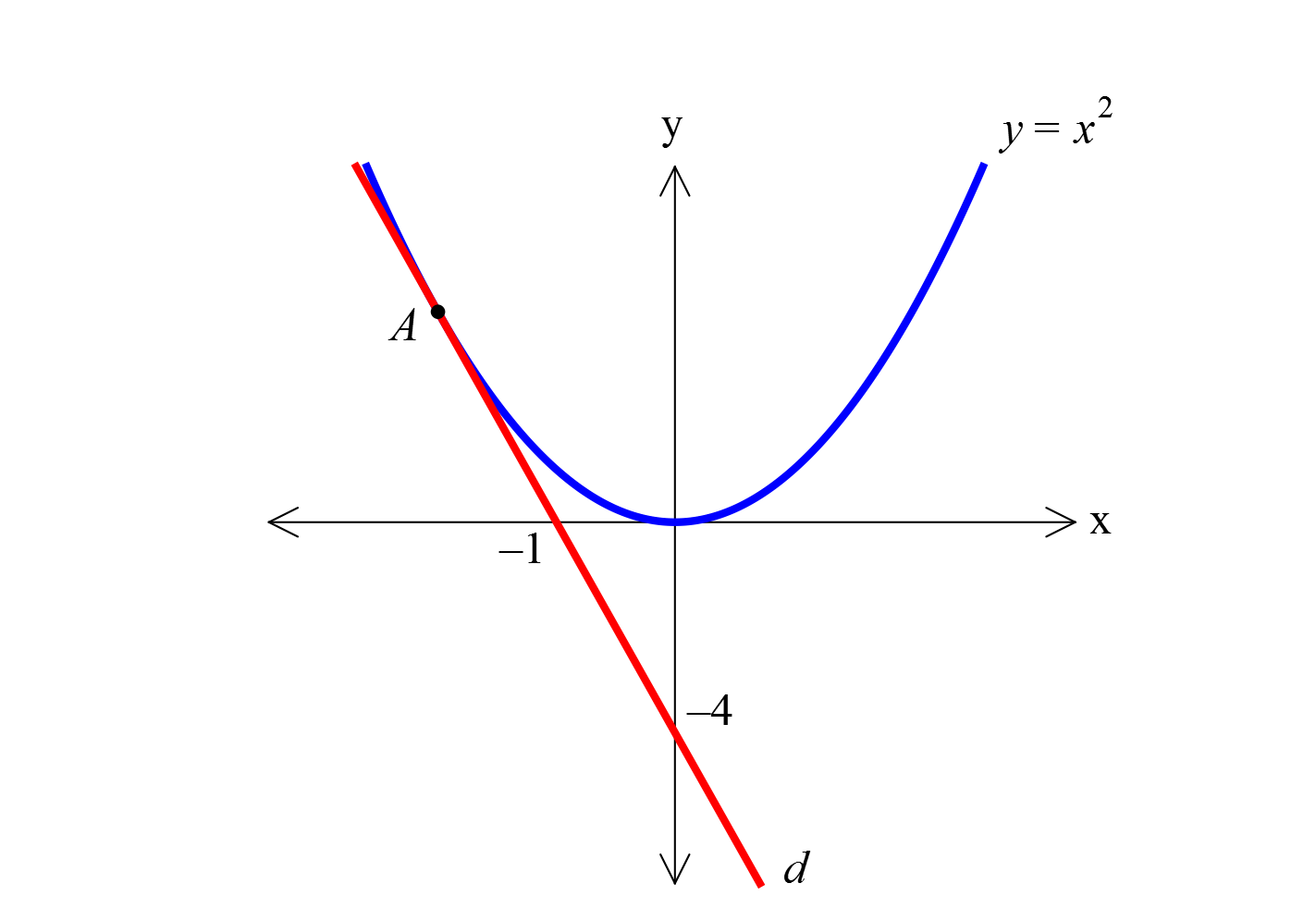
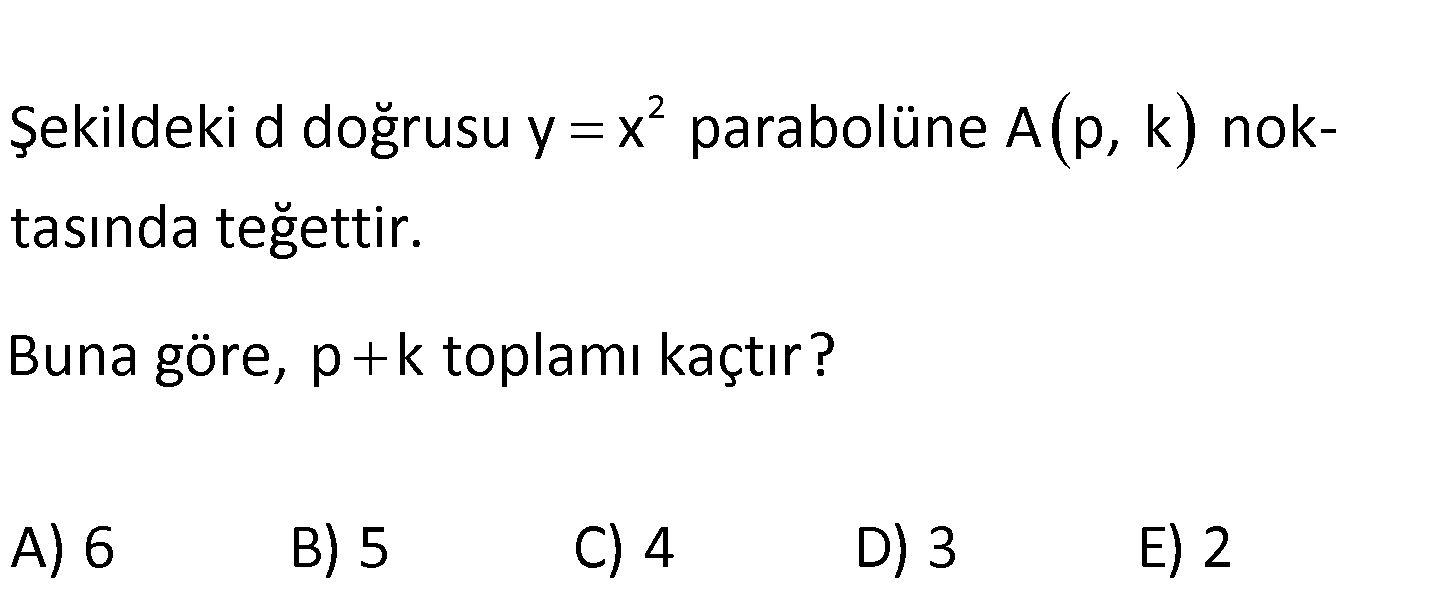
2 Şekildeki d doğrusu y x parabolüne A p, k noktasında teğettir. Buna göre, p k toplamı kaçtır? A B ) 6 ) 5 C) 4 D) 3 E) 2 www.matematikkolay.net 2 d doğrusunun denklemi: y x 1 y 4x 4 4 1 y 4x 4 tür y x : . Çözüm 2 2 2 2 parabolu ile kesişim noktasını bulalım. x 4x 4 x 4x 4 0 (x 2) 0 x 2 noktasıdır. x 2 için y x 4 tür. A(p,k) ( 2,4) p k 2 buluruz. 16

