Soru Sor sayfası kullanılarak Özel Üçgenler konusu altında 30-60-90 Üçgeni ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

3.SORU
4.SORU

5.SORU

6.SORU

7.SORU
8.SORU
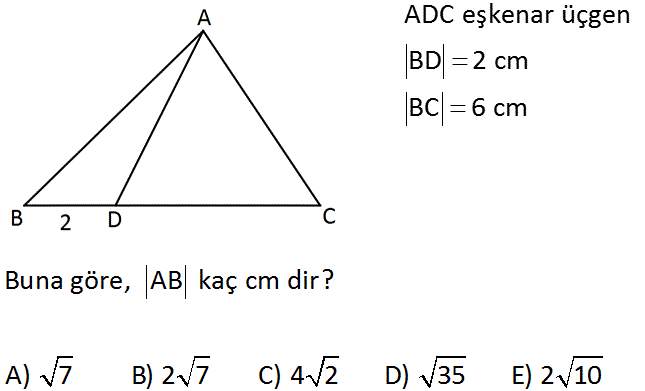

9.SORU


10.SORU
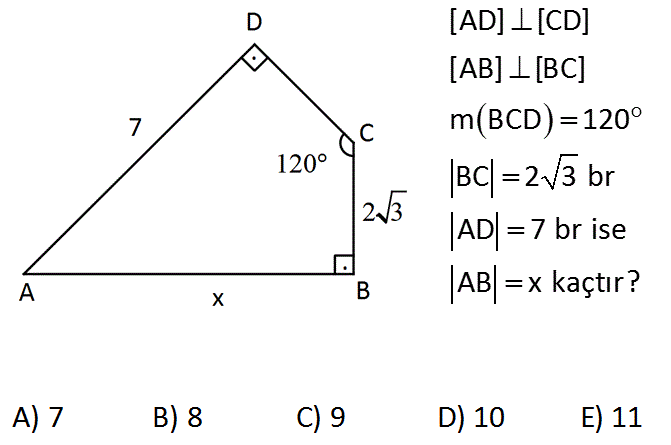

11.SORU

12.SORU
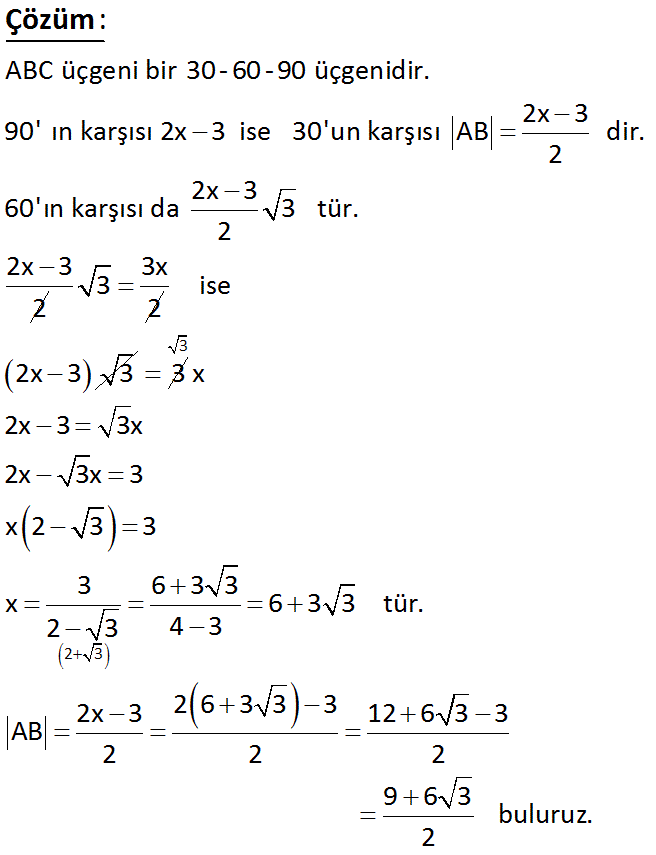
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
ABC bir dik üçgen AB BC m BCA 30 AC 8 cm Yukarıdaki verilere göre, BC x kaç cm dir? A) 3 B) 4 C) 4 2 D) 4 3 E) 7 Çözüm: www.matematikkolay.net ABC üçgeni 30 60 90 üçgenidir. Bu üçgende 30 nin karşısı hipotenüsün yarısıdır. Bu sebeple; 8 AB 4 cm dir. 2 60 nin karşısı, 30 nin karşısının 3 katıdır. x 4 3 cm buluruz. 55
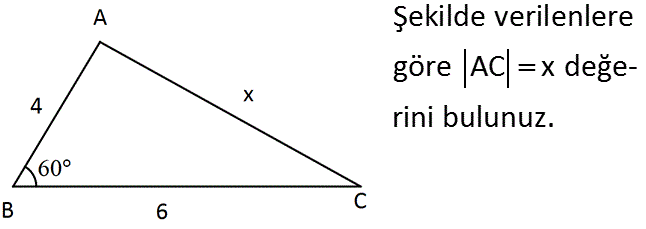
Şekilde verilenlere göre AC x değerini bulunuz. Çözüm: 2 A kenarından bir dikme indirirsek, sol tarafta bir 30 -60 -90 üçgeni oluşur. 90’ın karşısındaki kenar 4 ise; 30’un karşısındaki kenar 2 ; 60’ın karşısındaki kenar 2 3 tür. ADC üçgeninde pisagordan; x (2 32 2 2 2 ) 4 x 12 16 x 28 x 2 7 buluruz. 3
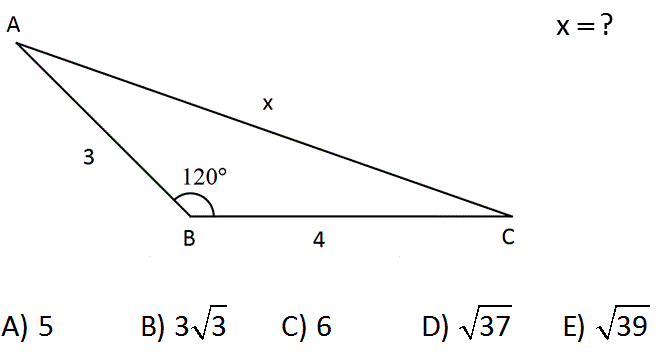
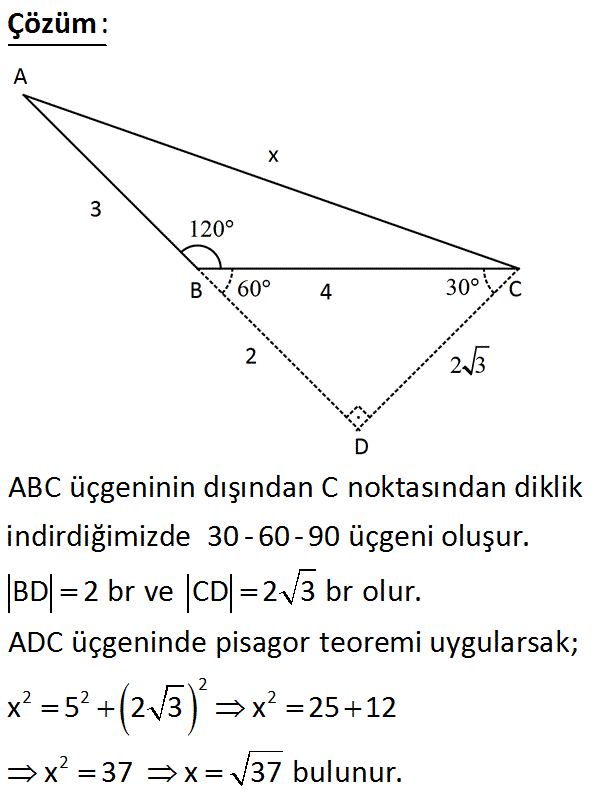
x ? A) 5 B) 3 3 C) 6 D) 37 E) 39 www.matematikkolay.net : Çözüm 2 2 2 2 2 ABC üçgeninin dışından C noktasından diklik indirdiğimizde 30 – 60 – 90 üçgeni oluşur. BD 2 br ve CD 2 3 br olur. ADC üçgeninde pisagor teoremi uygularsak; x 5 2 3 x 25 12 x 37 x 37 bulunur. 5
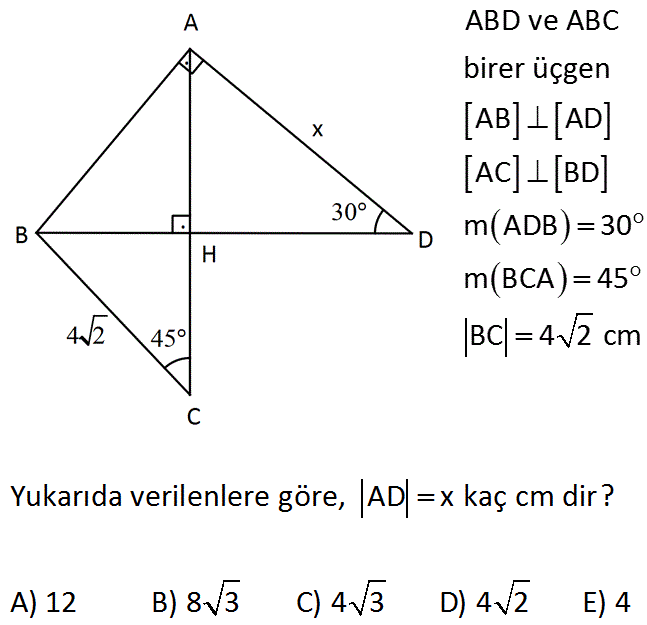
www.matematikkolay.net ABD ve ABC birer üçgen AB AD AC BD m ADB 30 m BCA 45 BC 4 2 cm Yukarıda verilenlere göre, AD x kaç cm dir? A) 12 B) 8 3 C) 4 3 D) 4 2 E) 4 : Çözüm www.matematikkolay.net BHC üçgeni 45 45 90 üçgeni olduğundan BH 4 cm dir. ABH üçgeni 30 60 90 üçgeni olduğundan; 30 nin karşısında 4 var sa 60 nin karşısında 4 3 cm vardır. AHD üçgeninde 30 nin karşısında 4 3 cm varsa 90 nin k arşısında 8 3 cm bulunur. 22
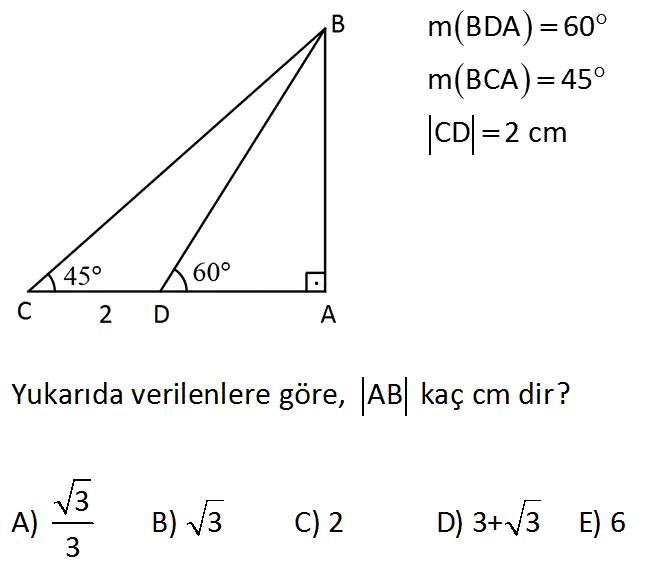
www.matematikkolay.net m BDA 60 m BCA 45 CD 2 cm Yukarıda verilenlere göre, AB kaç cm dir? 3 A) B) 3 C) 2 D) 3+ 3 E) 6 3 Çözüm: www.matematikkolay.net 2 2 2 2 2 2 2 x 2 x 3 kare alalım x 4x 4 3x 2x 4x 4 0 x 2x 2 0 İkinci derecede denklemde kök hesabı: b ax bx c 0 , b 4ac , x 2a 2 4.1. 2 4 8 12 2 12 2 2 3 x 1 3 2 2 Uzunluk pozitif olmal ı 1 3 alınır. AB x 3 1 3 . 3 3 3 bulunur. 28
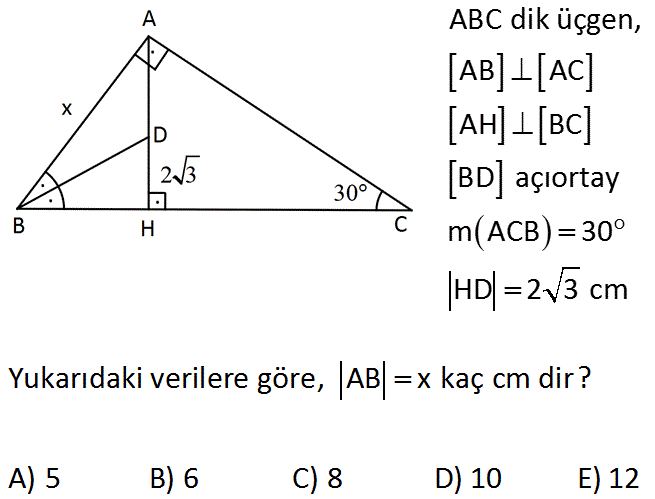
www.matematikkolay.net ABC dik üçgen, AB AC AH BC BD açıortay m ACB 30 HD 2 3 cm Yukarıdaki verilere göre, AB x kaç cm dir? A) 5 B) 6 C) 8 D) 10 E) 12 : Çözüm m(ACB) 30 ise m(ABH) 180 90 30 60 dir. Açıortaydan dolayı m(DBH) 60 / 2 30 dir. BDH üçgeni bir 30 -60 -90 üçgenidir. 30’un karşısı 2 3 ise, 60’ın karşısı 2 3. 3 6 cm ABH üçgeni de 30 -60 -90 üçgenidir. 30′ un karşısı 6 ise, 90’ın karşısı 12’dir. Cevap: 12 34
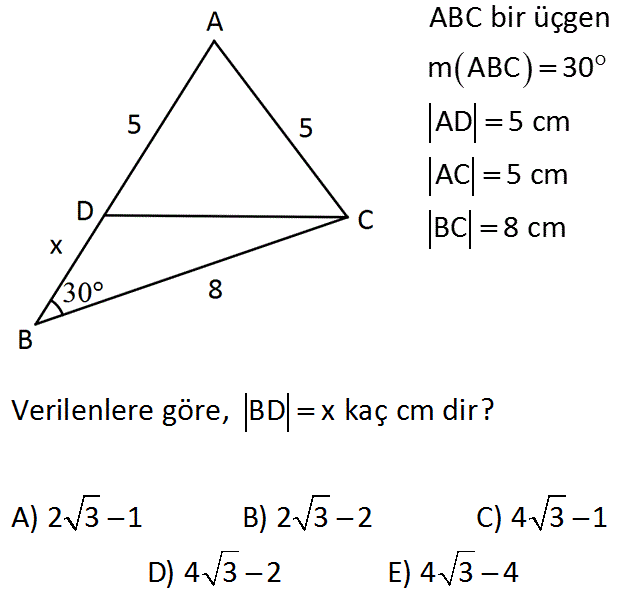
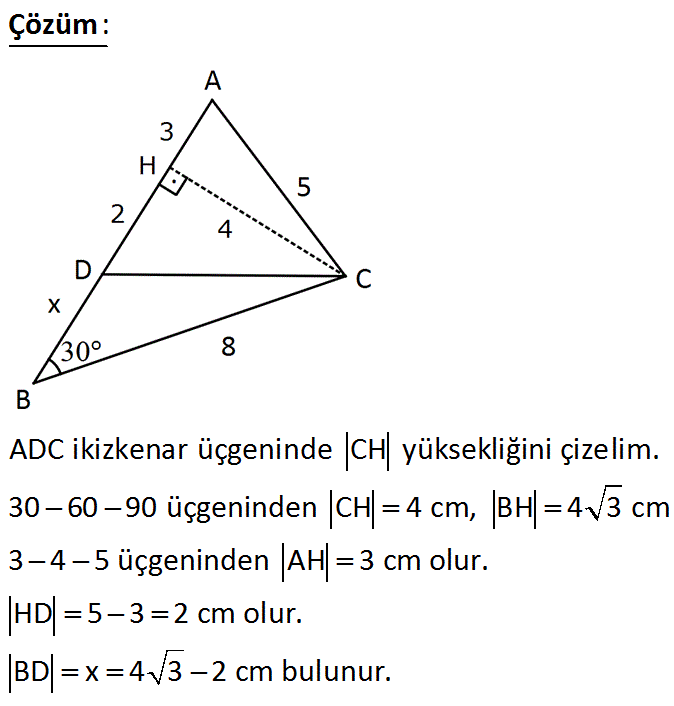
www.matematikkolay.net ABC bir üçgen m ABC 30 AD 5 cm AC 5 cm BC 8 cm Verilenlere göre, BD x kaç cm dir? A) 2 3 1 B) 2 3 2 C) 4 3 1 D) 4 3 2 E) 4 3 4 : Çözüm ADC ikizkenar üçgeninde CH yüksekliğini çizelim. 30 60 90 üçgeninden CH 4 cm, BH 4 3 cm 3 4 5 üçgeninden AH 3 cm olur. HD 5 3 2 cm olur. BD x 4 3 2 cm bulunur. www.matematikkolay.net 39
ADC eşkenar üçgen BD 2 cm BC 6 cm Buna göre, AB kaç cm dir? A) 7 B) 2 7 C) 4 2 D) 35 E) 2 10 Çözüm: www.matematikkolay.net DC 6 2 4 cm dir. ADC eşkenar üçgeninde AH yüksekliği indirilirse taban iki eş parçaya bölünür. DH HC 2 cm 60 nin karşısında 30 nin karşısındaki kenarın 3 katı bulunur. AH 2. 3 2 3 bulunur. ABH üçgeninde pis 2 2 2 2 2 2 2 2 agor uygulayalım; AB AH BH AB 2 3 4 AB 4.3 16 AB 28 AB 28 4.7 2 7 cm bulunur 43
[AB] [AC] BC 12 xm 30 m C 60 Verilenlere göre, AC nin alabileceği tam sayı değerlerinin toplamı kaç cm dir? A) 31 B) 32 C) 33 D) 34 E) 35 www.matematikkolay.net C açısı 30 olsaydı, B açısı 60 olurdu. 12 30 -60 -90 üçgenine göre 30’un karşısı 6 ; 2 60’ın karşısı 6 3 tür. |AC| 6 3 olur. C açısı 60 olsaydı, B açısı 30 olurdu. 30 -60 -90 üçgenin : e göre 30’un Çözüm 12 karşısı 6 ; 2 |AC| 6 olur. Buna göre; 6 |AC| 6 3 olmalıdır. 6 3 36.3 108 ‘den küçük en büyük tam sayı 10 olduğundan; |AC| 7,8,9 ve 10 olabilir. Toplamları 34 buluruz. 9
[AD] [CD] [AB] [BC] m BCD 120 BC 2 3 br AD 7 br ise AB x kaçtır ? A) 7 B) 8 C) 9 D) 10 E) 11 Çözüm: AEB üçgeni 30 -60 -90 üçgenidir. Buna göre; 2 (x 3 2 3) (2x 7) 3 (x 3 2 3) 3 (2x 7) 2 3x 6 4x 14 x 8 buluruz. www.matematikkolay.net 2
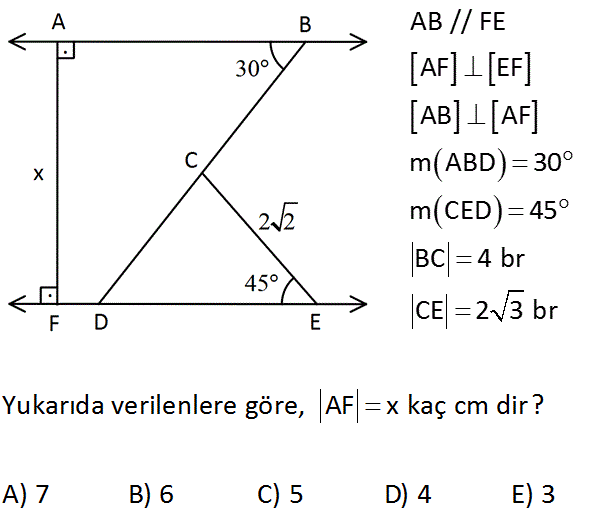
www.matematikkolay.net AB // FE AF EF AB AF m ABD 30 m CED 45 BC 4 br CE 2 3 br Yukarıda verilenlere göre, AF x kaç cm dir? A) 7 B) 6 C) 5 D) 4 E) 3 : Çözüm Şekildeki gibi AF ye paralel olarak GH doğrusunu çizelim. Burada BCG ve CHE dik üçgenlerini oluşur. BCG bir 30 -60 -90 üçgenidir. Hipotenüs 4 birim ise 30 nin karşısı bunun yarısıdır. 4 GC 2 birimdir. 2 CHE bir 45- 45-90 üçgenidir. Hipotenüs 2 2 birim ise dik kenarlar 2 birim olur. CH 2 birimdir. x AF GC CH 2 2 4 birim buluruz. www.matematikkolay.net 45
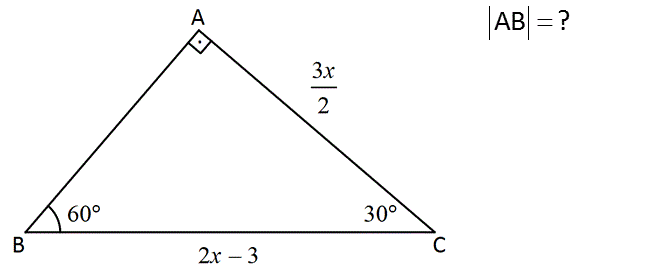
AB ? www.matematikkolay.net : Çözüm ABC üçgeni bir 30 -60 -90 üçgenidir. 2x 3 90’ ın karşısı 2x 3 ise 30’un karşısı AB dir. 2 2x 3 60’ın karşısı da 3 tür. 2 2x 3 2 3x 3 2 ise 2x 3 3 3 3 2 3 x 2x 3 3x 2x 3x 3 x 2 3 3 3 6 3 3 x 6 3 3 tür. 2 3 4 3 2x 3 2 6 3 3 3 12 6 3 3 AB 2 2 2 9 6 3 buluruz. 2 60

