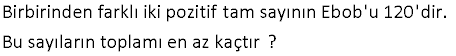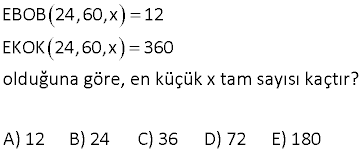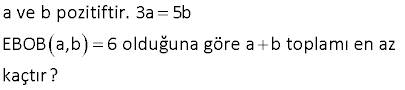Soru Sor sayfası kullanılarak EBOB EKOK konusu altında EBOB ve EKOK’tan sayıyı bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU


5.SORU


6.SORU


7.SORU


8.SORU


9.SORU


10.SORU
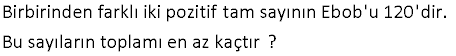

11.SORU


12.SORU
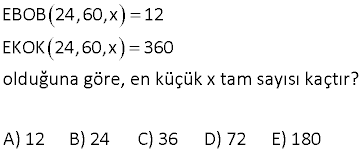

13.SORU


14.SORU
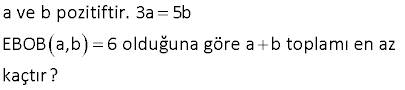

Diğer Soru Tipleri için Tıklayınız.
Soru Sormak için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çözümlü Test İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
a pozitif tam sayı olmak üzere, EKOK 6,a EBOB 24,a olduğuna göre, a’nın alabileceği değerlerin toplamı kaçtır? A) 24 B) 36 C) 42 D) 50 E) 57 Çözüm: EKOK(6, a) EBOB(24, a) 6, 12 veya 24 olabilir. 6 olursa a 6 dır. 12 olursa a 12 24 olursa a 24 olur. Değerler toplamı: 6 12 24 42 buluruz. 4 a ve b, 6’dan büyük birer doğal sayı olmak üzere, OBEB a,b 6 OKEK a,b 72 şeklinde veriliyor.Buna göre a b kaçtır? Çözüm: a 6x , b 6y olsun. 6.x.y 72 dir. x.y 12 x 3 ve y 4 tür. (veya tam tersi) Buna göre; a 6x 6.3 18 b 6y 6.4 24 a b 18 24 42 buluruz. 12 En küçük ortak katı 40 olan farklı iki doğal sayının toplamı en çok kaçtır? Çözüm: 40, bu iki sayının katıdır. 40’ı 1’e bölersek, olabilecek en büyük sayıyı buluruz. 40 40 1 40 Diğer en büyük sayı da 20 dir. 2 Toplamları 20 40 60 buluruz. 13 A,B,x,y pozitif tam sayılar, 18 27 A x x y y B 12 60 olduğuna göre A B toplamı en az kaçtır? A) 17 B) 14 C) 11 D) 9 E) 6 Çözüm: A’yı en küçük yapmak için, hem 18’i hem de 27’yi bölecek en büyük sayıyı bulalım. Bu sayı da 9 dur. Buna göre; 18 27 18 27 A 2.3 6 dır. x x 9 9 B’ yi en küçük yapmak için, hem 12’nin hem de 60’ın en küçük ortak katını bulalım. Bu sayı da 60 tır. Buna göre; 60 60 B 5.1 5 tir. 12 60 Toplam 6 5 11 buluruz. 14 a ile b birbirinden farklı pozitif tam sayılardır. EKOK a,b 30 olduğuna göre, a+b toplamının alabi ceği en büyük değer ile en küçük değerin farkı kaçtır? A) 24 B) 28 C) 30 D) 32 E) 34 Çözüm: EKOK(a,b) 30 a ve b’nin alacağı maksimum değer 30’dur. a b’nin en büyük değeri; a 30 olsun.b, a’dan farklı olacağı için en fazla 15 olur. a b 30 15 45 dir. a b’nin en küçük değeri; a ve b yi aralar ında asal seçersek, yani ebob(a,b) 1 olursa; a.b 30 olur. En küçük değer için sayıları birbirine yakın seçmeliyiz.Buna göre; a 6 ve b 5 olur. a b 6 5 11 dir. En büyük değer En küçük değer; 4511 34 bulunur. 24 3 a ve b pozitif tam sayı olmak üzere, EKOK a,b 3.2 eşitliğini sağlayan kaç farklı a,b sıralı ikilisi vardır? A) 24 B) 21 C) 18 D) 15 E) 12 3 3 3 Çözüm: EKOK(a, b) 3.2 a 3.2 olursa b Pozitif Bölen Sayısı kadar (1 1)(3 1) 2.4 8 dir. b 3.2 olursa a Pozitif Bölen Sayısı kadar 3 3 (1 1)(3 1) 2.4 8 dir. a ve b’nin ikisinin de 3.2 olduğu durumu 2 defa say dık; çıkarınca toplam 8 8 1 15 durum var dır. Şimdi ikisinden birinin 3.2 olmadığı durum 3 3 2 3 3 2 ları tes – pit edelim; a 3 olursa b 2 olmalı a 2.3 olursa b 2 olmalı 6 durum a 2.3 olursa b 2 olmalı a 2 olursa b 3 , 3.2 , 3.2 Toplam 6 15 21 durum vardır. 32 36, 45 ve A sayılarının EBOB’u 9 ve EKOK’u 360 olduğuna göre, bu koşula uyan en küçük A doğal sayısı kaçtır? A) 18 B) 27 C) 36 D) 54 E) 72 2 2 3 2 2 2 2 3 … 2 2 2 3 2 3 2 .. 2 2 Çözüm: 36,45,A sayılarının ebobu 9 ekok u 360 ise; ebob 36,45,A 2 .3 ,3 .5, A 3 ekok(36,45,A) 2 .3 ,3 .5, A 2 .3 .5 A sayısının içerisinde 3 olmak zorunda çünkü ebobları 3 , A sayısının içeri 3 3 3 2 sinde, 2 olmak zorunda çünkü ekoktaki 2 çarpanı diğer iki sayıdan gelemez. A’ nın en küçük değerini sorduğu için başka çarpan yazmamıza gerek yok. A 2 .3 72 bulunur. 33 a,12’nin ve a,15’in OBEB’leri toplamı 3 ise iki basamaklı en büyük ve en küçük a doğal sayılarının toplamı kaçtır? A) 100 B) 108 C) 110 D) 112 E) 113 Çözüm: OBEB’leri toplamı 3 olabilmesi için bunların 1 ve 2 olması lazım. (a, 15)’in OBEB’i 2 olamayacağı için; OBEB(a, 12) 2 dir. OBEB(a, 15) 1 dir. Yani a sayısı 2’nin bir katıdır ve 15 ile araların da asaldır. Bu şarta uygun iki basamaklı en küçük sayı 14′ tür. En büyük sayı da 98’dir. Toplamları 14 98 112 buluruz. 38 a ile b birbirinden farklı pozitif tam sayılardır. EKOK a,b 30 olduğuna göre, a b toplamının alabileceğine en büyük değer ile en küçük değerin farklı kaçtır? Çözüm: Ekok(a,b) 30 a.b Ekok(a,b).Ebob(a,b) a b nin en küçük değeri için a.b yi olabildiğince küçük tutmalıyız.Eğer sayılar aralarında asal olsa yani Ebob(a,b) 1 olsa; a.b Ekok(a,b) 30 olur. Sayılar araları nda asal olduğundan; a 6 ve b 5 alabiliriz. a b 6 5 11 olur. a b nin en büyük değeri için ise a ve b yi olabildiğince büyük almalıyız.Sayılar ekoklarından büyük olamaz. Bu yüzden a’yı en fazla 30 alabilir iz. b’yi de a’dan farklı olacak şekilde en fazla 15 alabiliriz. a b 30 15 45 olur. 45 11 34 bulunur. 40 Birbirinden farklı iki pozitif tam sayının Ebob’u 120’dir. Bu sayıların toplamı en az kaçtır ? Çözüm: İki sayının ebob’u 120 ise ikisi de 120’nin tam katı olmalıdır.Toplamlarının en az olması için sayılardan biri 120 olmalı.Diğer bundan farklı 120’nin katı olan en küçük sayı seçilmeli.O da 120.2 240 olur. 120 240 360 bulunur. a ve b pozitiftir. 3a 5b EBOB a,b 6 olduğuna göre a b toplamı en az kaçtır? Çözüm: 3a 5b a 5k, b 3k Ebob a,b 6 k 6 dır. a 5.6 30 b 3.6 18 30 18 48 bulunur.