Soru Sor sayfası kullanılarak Logaritma konusu altında Logaritmik Problemler ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
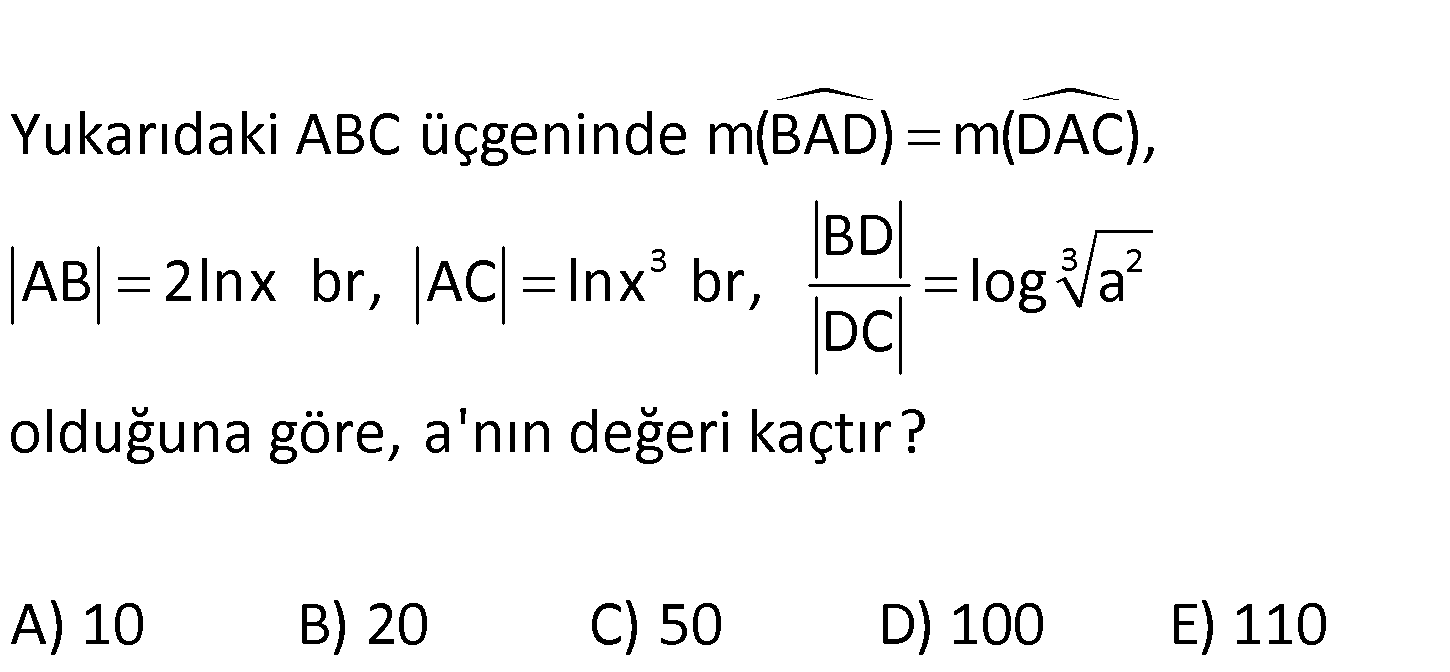
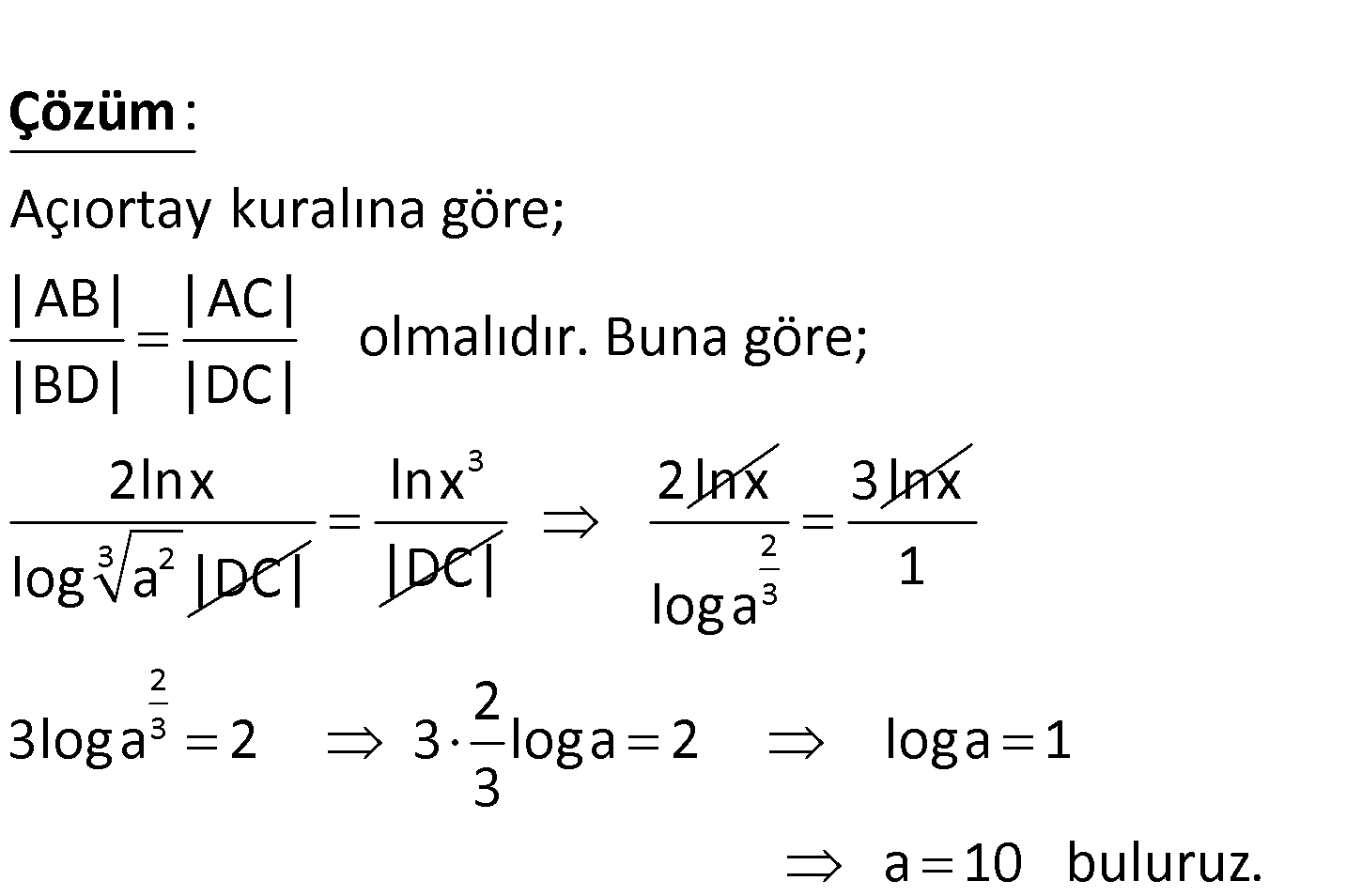
3.SORU
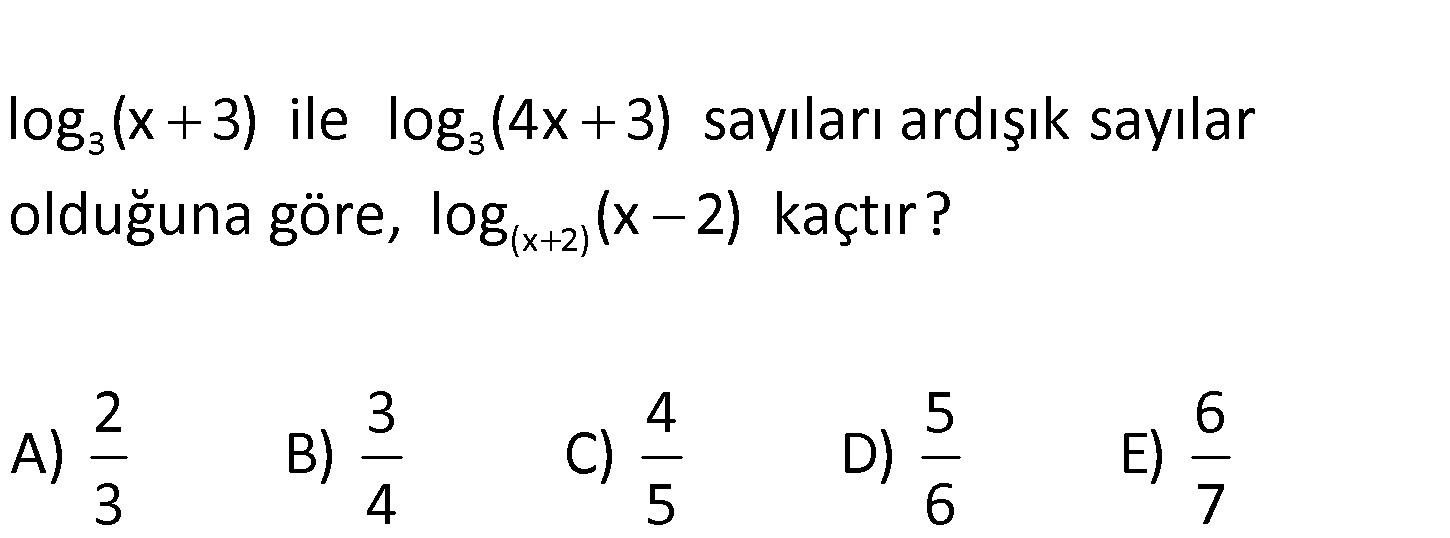

4.SORU

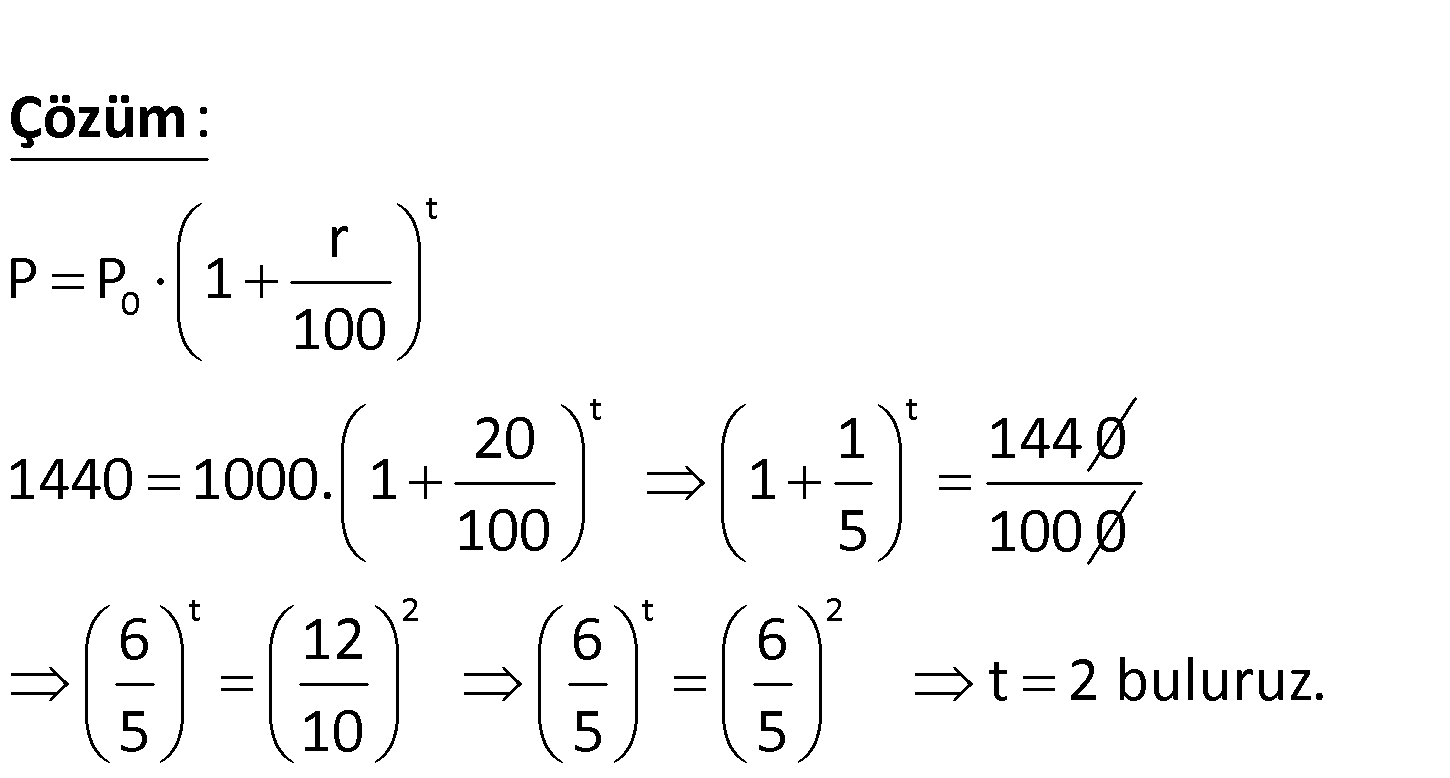
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
200 TL parası olan bir kimse her ay,bir önceki aydaki parasının %2 sini, biriktirdiği paraya ilav e ediyor. Buna göre, kaç ay sonra toplam parası 300 TL olur? log 1,02 0,008 log 1,25 0,096 log(1,5) 0,176 log 2 0,3 www.matematikkolay.net Her ay %2’sini biriktiriyorsa; 102 1 ay sonunda parası 200 olur. 100 1 2 ay sonunda parası 2 : 0 Çözüm 2 x x 2 olur. 100 102 x ay sonunda parası 200 olur. 100 102 300 200 olması isteniyor. 100 3 00 2 00 x x x x . 1,02 3 1,02 2 1,5 1,02 İki tarafında log’unu alalım. log 1,5 log 1,02 log 1,5 xlog 1,02 log 1,5 0,176 176 x x 22 buluruz. log 1,02 0,008 8 133
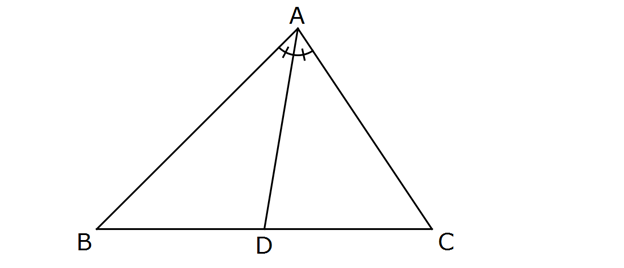
3 3 2 Yukarıdaki ABC üçgeninde m(BAD) m(DAC), BD AB 2lnx br, AC lnx br, log a DC olduğuna göre, a’nın d eğeri kaçtır? A) 10 B) 20 C) 50 D) 100 E) 110 3 2 Açıortay kuralına göre; |AB| |AC| olmalıdır. Buna göre; |BD| |DC| 2lnx log a | C| : D Çözüm 3 lnx |DC| 2lnx 2 3 3lnx loga 2 3 1 2 3loga 2 3 loga 2 loga 1 3 a 10 buluruz. www.matematikkolay.net 93
3 3 (x 2) log (x 3) ile log (4x 3) sayıları ardışık sayılar olduğuna göre, log (x 2) kaçtır? 2 3 A) B) 3 4 5 6 C) D) E) 4 5 6 7 www.matematikkolay.net 3 3 3 3 3 3 3 Ardışık sayılar ise; log 4x 3 log x 3 1 olmalıdır. log 4x 3 1 log x 3 log 4x 3 log 3 log x : 3 lo Çözüm 3 3 3 2 x 2 8 2 g 4x 3 log 3 x 3 4x 3 3 x 3 4x 3 3x 9 x 6 dır. Buna göre; 2 log x 2 log 4 log 2 buluruz. 3 150
0 P Ana para r Yıllık faiz oranı t Süre(yıl) P Faiz Ana Para olmak üzere, ban t 0 kaya yatırılan bir miktar paranın bileşik faiz formülü, r P P 1 şeklindedir. 100 1000 TL, yıllık %20 faiz oranıyla kaç yıllığına banka – ya yatırılırsa, bu sürenin sonunda bankadan 1440 TL o larak çekilir. A) 6 B) 5 C) 3 D) 2 E) 1 www.matematikkolay.net t 0 t t r P P 1 100 20 1 144 0 1440 1000. 1 1 10 5 : 0 Çözüm 100 0 t 2 t 2 6 12 6 6 t 2 buluruz. 5 10 5 5 53

