Soru Sor sayfası kullanılarak Logaritma konusu altında Logaritmik Eşitsizlikler, Logaritma Aralık Bulma, Logaritma Sıralama ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU

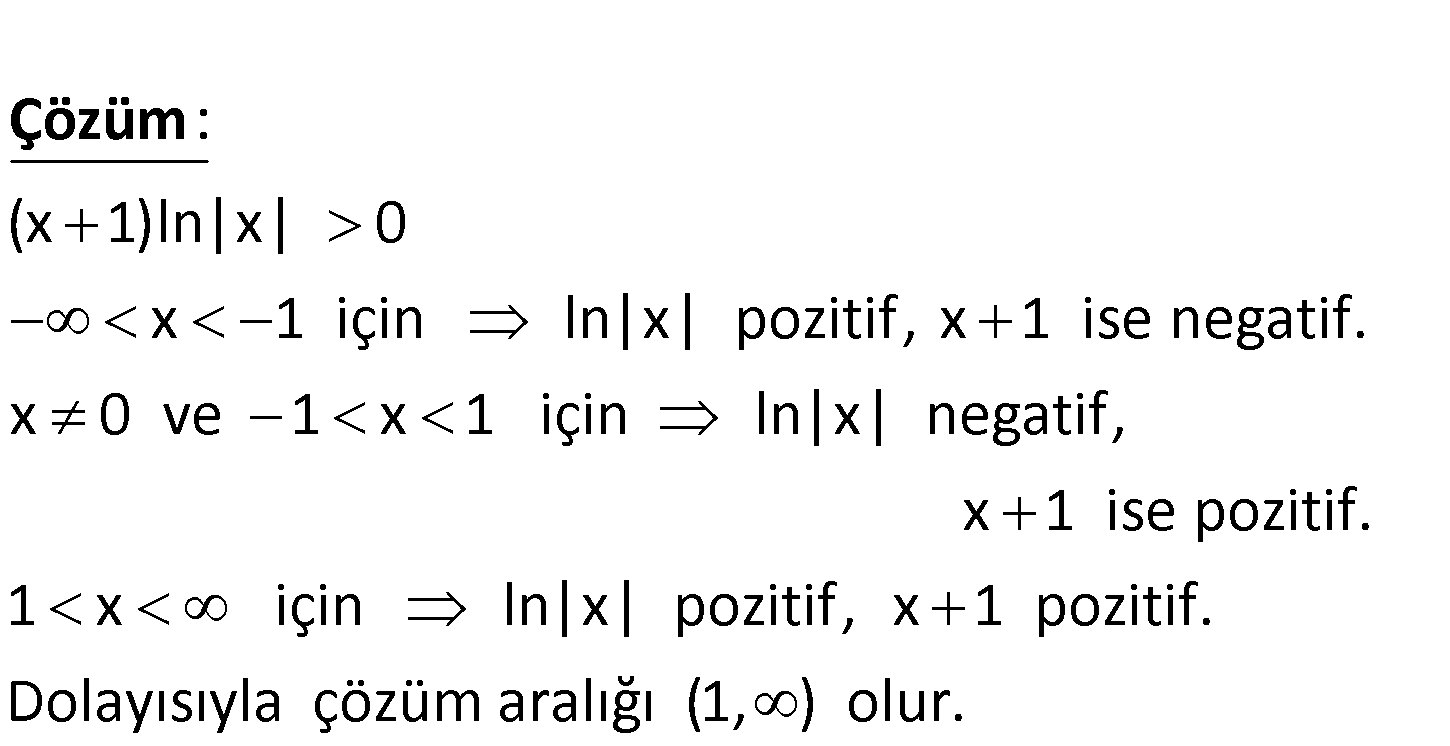
4.SORU


5.SORU


6.SORU


7.SORU
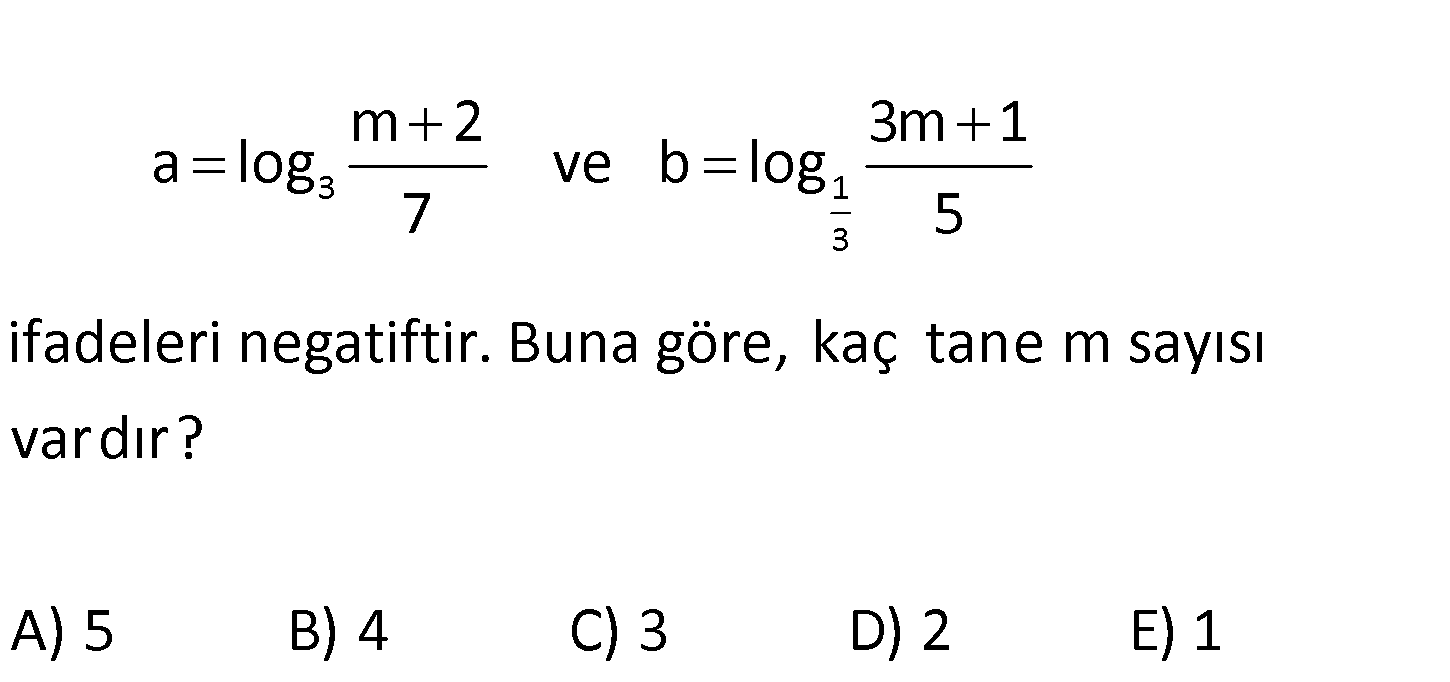
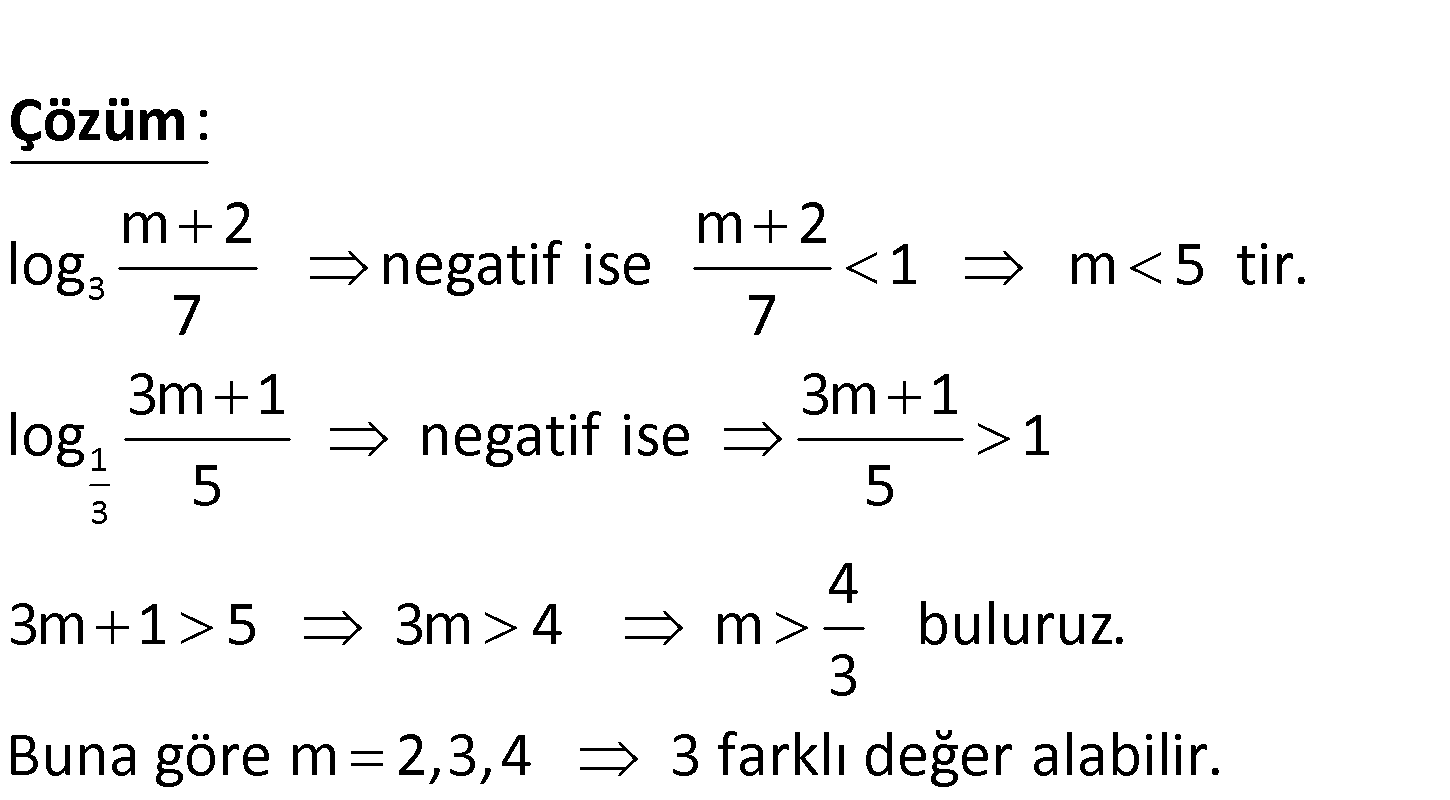
8.SORU


9.SORU


10.SORU


11.SORU
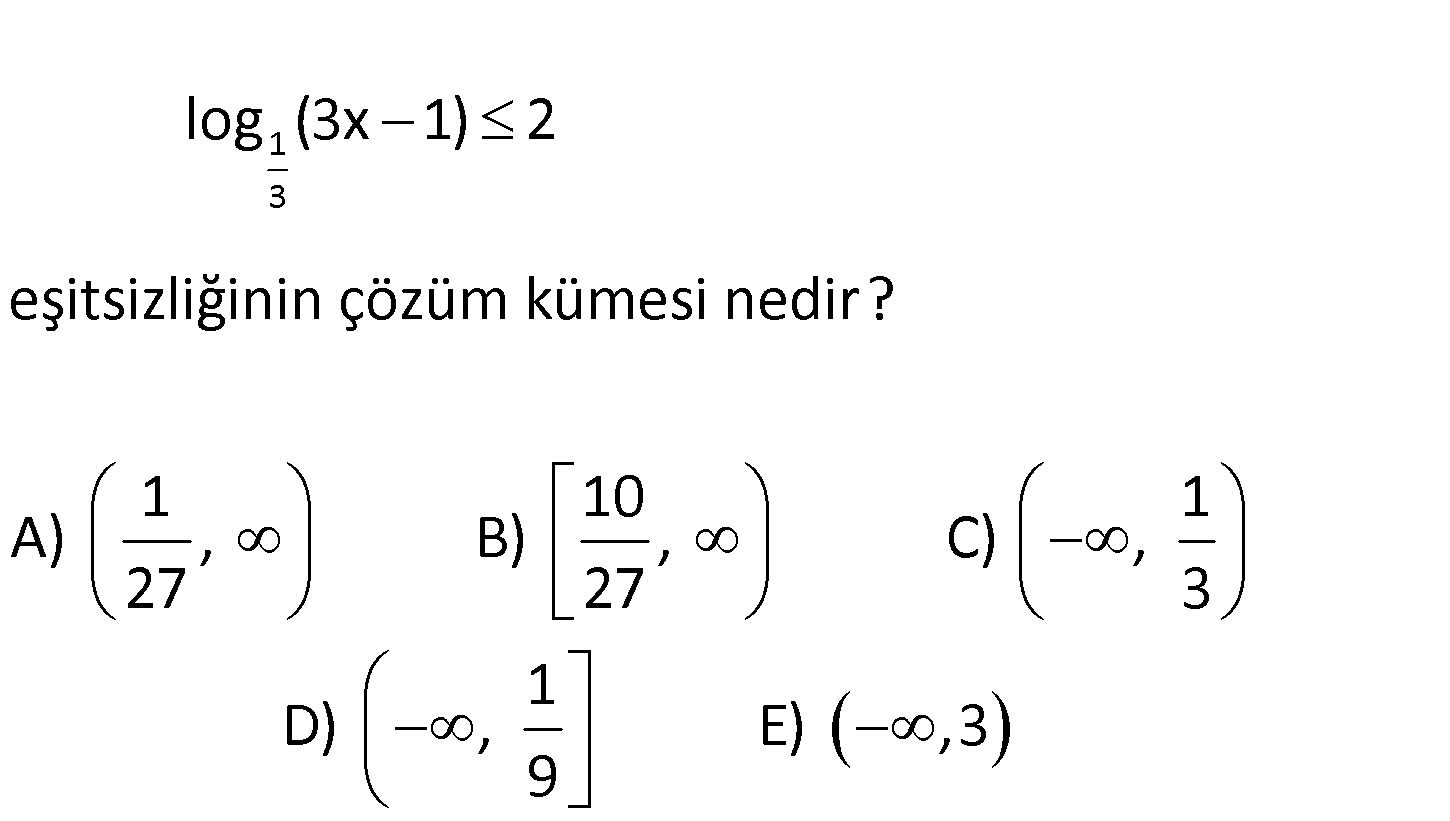
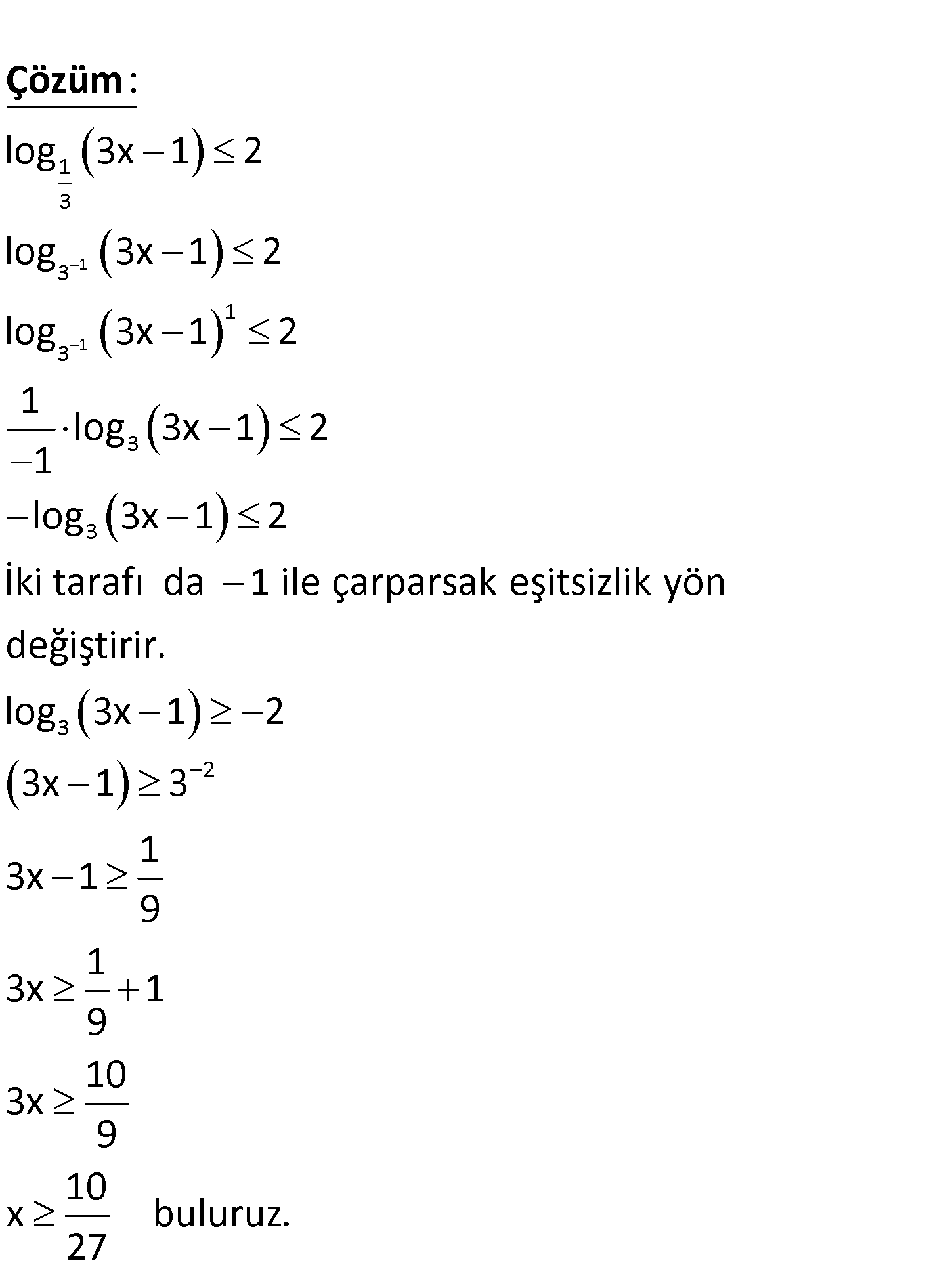
12.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
8 3 2 log 1 log (x 2) log 16 koşulunu gerçekleyen en çok kaç tane tamsayı vardır? A) 65 B) 71 C) 79 D ) 81 E) 86 8 3 2 0 4 3 0 4 log 1 log (x 2) log 16 0 log (x 2) 4 3 x 2 3 1 x 2 81 1 x 79 Bu aralıktaki tamsayılar 7 : Çözüm 9 ( 1) 1 81 tanedir. Cevap: 81 www.matematikkolay.net 4
1 5 log (x 2) 2 eşitsizliğinin çözüm aralığını bulunuz. www.matematikkolay.net 1 5 log (x 2) 2 log(x 2) 2 1 log 5 log(x 2) 2 log5 log(x 2) 2log5 ( Negatif bir değer ile : Çözüm 2 çarpıldığı için eşitsizlik yön değiştirir.) log(x 2) log5 1 49 x 2 x buluruz. 25 25 Ayrıca, tanım gereği log aritmanın içi pozitif olmalıdır. x 2 0 x 2 dir. 49 Buna göre çözüm aralığı: 2, 25 buluruz. 46
(x 1)ln x 0 eşitsizliğinin çözüm kümesi aşağıdakilerden hangi – sidir? A) ( , e) (e, ) B) (1, ) C) R D) ( , e) ( 1, ) E) R [ 1, 1] www.matematikkolay.net (x 1)ln|x| 0 x 1 için ln|x| pozitif, x 1 ise negatif. x 0 ve 1 x 1 için l : n|x| Çözüm negatif, x 1 ise pozitif. 1 x için ln|x| pozitif, x 1 pozitif. Dolayısıyla çözüm aralığı (1, ) olur. 66
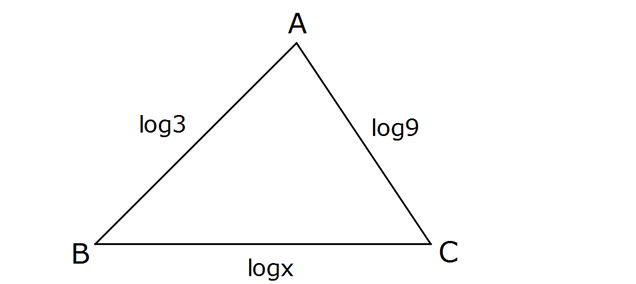
Yukarıdaki ABC üçgeninde verilenlere göre, x’in ala – bileceği en büyük tam sayı değeri kaçtır? A) 27 B) 26 C) 21 D) 15 E) 8 Üçgende açı kenar bağıntısına göre; Bir kenar,diğer iki kenarın toplamından küçük, farkla : rında Çözüm n da büyüktür. Buna göre; log9 log3 logx log3 log9 9 log logx log 3.9 3 log3 logx log27 3 x 27 x en fazla 26 olabilir. www.matematikkolay.net 92
a b log 5 log 5 0 olduğuna göre, aşağıdakilerden hangisi kesinlikle doğrudur? A) 1 a b B) 0 b 1 a C) 0 a 1 b D) 0 b a 1 E) 0 a b 1 a b log 5 log 5 0 İki log aritmanın da değeri negatif ise; a ve b değerleri 1 den küçük olma : lıdır. Ö Çözüm 01.May 1/5 1/25 rneğin; log 5 1 dir. Logaritmanın tanımı gereği tabanlardan 0’dan büyük olmak zorundadır. 0 a ve b 1 Ayrıca, 1 log 5 1 iken log 5 dir. 2 Yani, taban değeri küçüldükçe, log aritmanın d eğeri artıyor. b a olmalıdır. Buna göre; 0 b a 1 olmalıdır. 94
x y z 0 x y 1 z ve a log 3, b log 3 ve c log 3 olduğuna göre, aşağıdakilerden ha ngisi doğrudur? A) c a b B) a c b C) a b c D) b c a E) b a c www.matematikkolay.net x 1 9 Kolay işlem yapabileceğimiz değerler verelim. 1 1 x , y , z 3 olsun. 9 3 a log 3 log 3 log : Çözüm 2 1 1 3 1 y 1 3 3 z 3 1 1 3 dir. 2 2 1 b log 3 log 3 log 3 1 dir. 1 c log 3 log 3 1 dir. Buna göre; sıralama b a c olur. 95
3 1 3 m 2 3m 1 a log ve b log 7 5 ifadeleri negatiftir. Buna göre, kaç tane m sayısı vardır? A) 5 B) 4 C) 3 D) 2 E) 1 3 1 3 m 2 m 2 log negatif ise 1 m 5 tir. 7 7 3m 1 3m 1 log negatif ise 1 5 5 3m 1 5 3m : Çözüm 4 4 m buluruz. 3 Buna göre m 2,3,4 3 farklı değer alabilir. 100
2 2 log (x 9) 4 eşitsizliğini sağlayan kaç farklı x tam sayısı var dır? A) 10 B) 7 C) 6 D) 5 E) 4 2 2 2 4 2 2 log (x 9) 4 x 9 2 x 9 16 x 25 5 x 5 aralığındadır. Ancak logaritmanın içi pozi : tif Çözüm 2 2 olmalıdır. x 9 0 x 9 x 3 veya x 3 olmalıdır. Bu şartlara uyan tam sayılar; 5, 4,4,5 4 tane buluruz. 106
www.matematikkolay.net x 1 2 1 f(x) 4 ve g(x) log x fonksiyonları veriliyor. (gof )(x) 1 eşitsizliğini sağlayan kaç f arklı x tam sayısı var dır? A) 59 B) 58 C) 57 D) 56 E) 55 x 1 x 1 4 4 f(x) fonksiyonunun tersini bulalım. f(x) 4 y 4 log y x 1 log y 1 : Çözüm 1 4 1 4 2 4 4 4 2 4 x f (x) log x 1 tir. (gof )(x) 1 ise; g(log x 1) 1 log (log x 1) 1 şeklinde yazabiliriz. log x 1 2 log x 3 x 64 olmalıdır. Ayrıca; logaritmanın içi negatif olamayacağı için log ( log 4 0’dan büyük olmalı 4 x 1 ) 1 log x 1 0 log x 1 x 4 tür. x’in alabileceği değerler 5,6,..,63 63 5 1 59 tane 113
2 log (x 4) 4 eşitsizliğini sağlayan x ‘in alabileceği tamsayı değer – leri toplamı kaçtır? A) 1 66 B) 170 C) 172 D) 180 E) 182 www.matematikkolay.net 2 4 log (x 4) 4 x 4 2 x 4 16 x 20 dir. Logaritmanın tanımı gereği, log aritmanın içi p : ozitif olmald Çözüm ır. x 4 0 x 4 tür. x’in değerleri; 5,6,…,19 Toplamı Terim sayısı.Ortalama 19 5 (19 5 1).( ) 15.12 180 buluruz. 2 116
www.matematikkolay.net 1 3 log (3x 1) 2 eşitsizliğinin çözüm kümesi nedir? 1 10 1 A) , B) , C) , 27 27 3 1 D) , E) ,3 9 1 1 1 3 3 1 3 3 3 log 3x 1 2 log 3x 1 2 log 3x 1 2 1 log 3x 1 2 1 log 3x 1 2 İki tarafı da 1 ile ça a : rp rs Çözüm 3 2 ak eşitsizlik yön değiştirir. log 3x 1 2 3x 1 3 1 3x 1 9 1 3x 1 9 10 3x 9 10 x buluruz. 27 www.matematikkolay.net 135
Aşağıdaki ifadelerden hangisi tanımlı olduğu ara – lıkta azalan ve sadece (2,3) aralığında pozitif d 1 3 4 1 1 3 5 5 eğer – lidir? A) log (x 2) B) log (x 2) C) log (x 2) D) log (x 2) E) log (x 2) www.matematikkolay.net Logaritmanın azalan olması için, tabandaki sayının üssü negatif bir sayı olmalıdır : . Yani 0 Çözüm 1 1 4 ile 1 ara- 1 sında bir sayı olacaktır. Örneğin: 4 4 2 ile 3 arasında pozitif olması için de , logaritmanın içinin de 0 ile 1 arasında bir değer alması gerekir. log (x 2) bu şartlara uymaktadır. DOĞRU Cevap: A şıkkı 41

