Soru Sor sayfası kullanılarak Logaritma konusu altında Logaritma grafiği ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

3.SORU

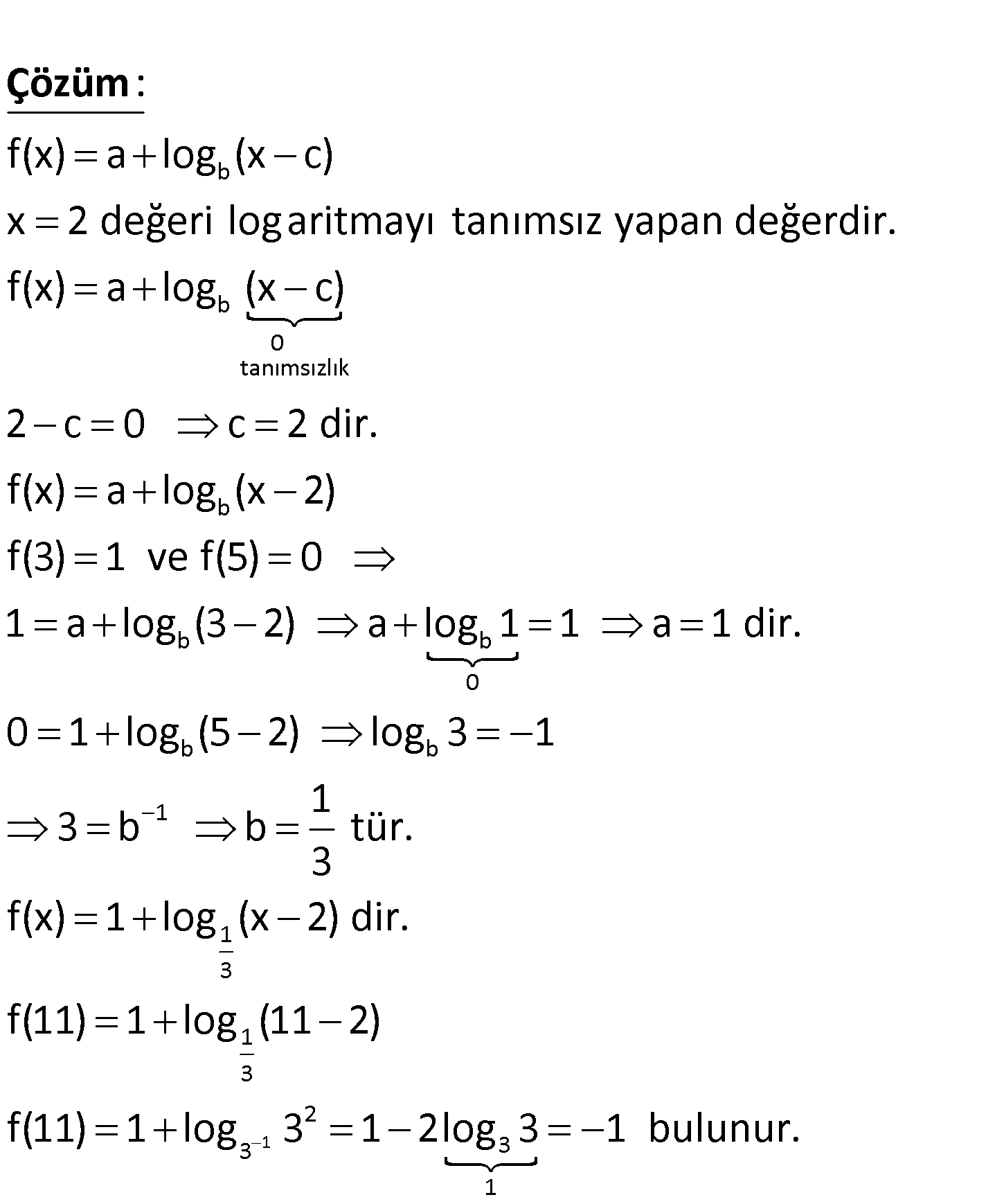
4.SORU

5.SORU


6.SORU
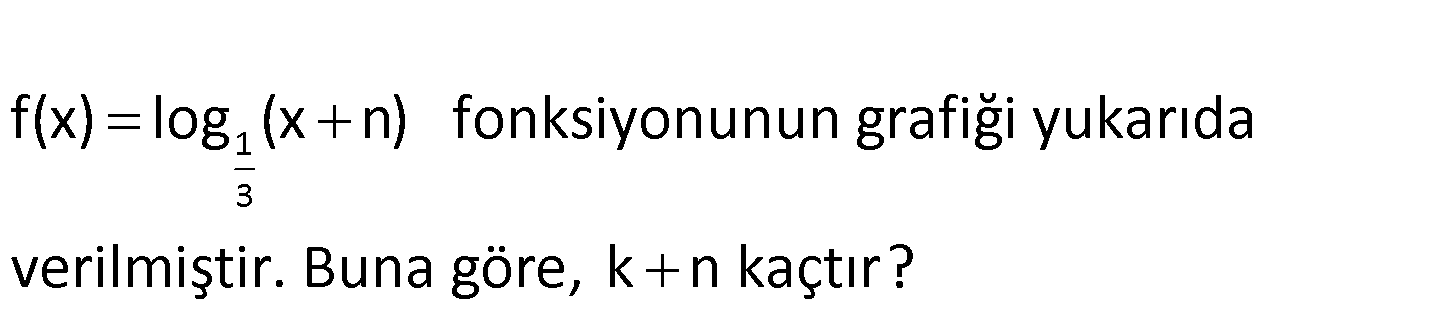

7.SORU
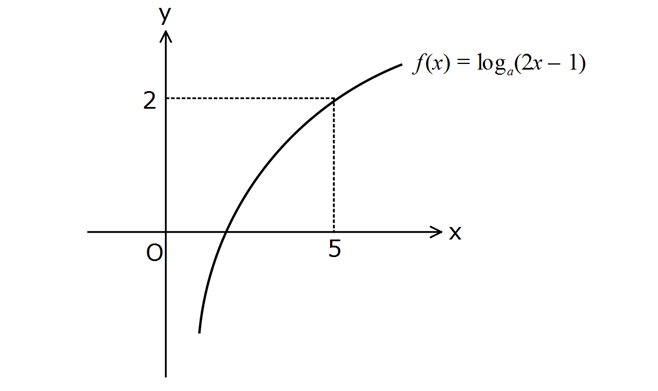
Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
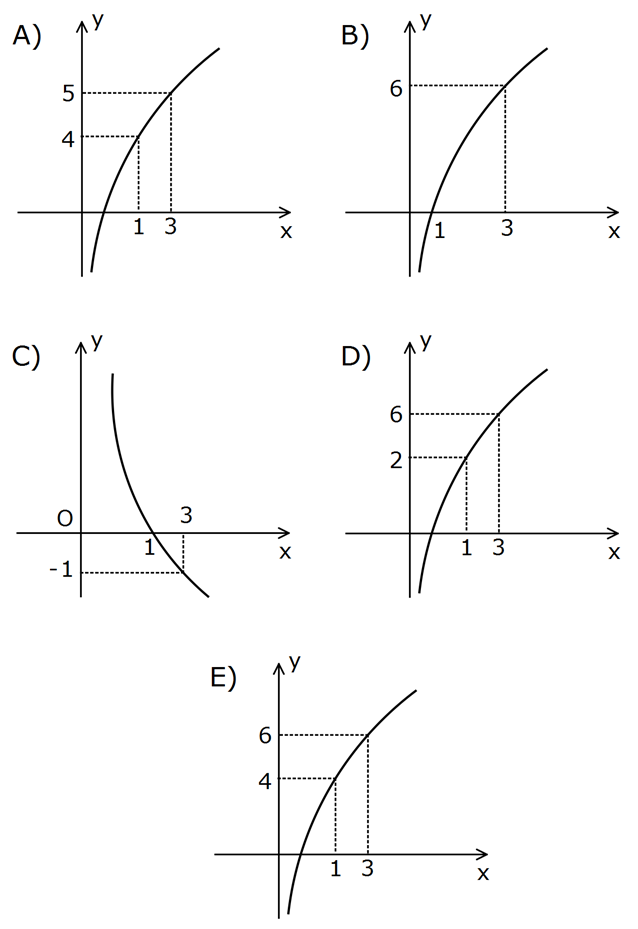
3 f(x) 2.log x 4 fonksiyonunun grafiği aşağıdakilerden hangisi olabilir? www.matematikkolay.net 3 3 f(x) 2log x 4 x 1 için f(1) 2log 1 4 4 tür. Bu duruma sadece A ve E şıkkı uy : uyor. x 3 içi Çözüm 3 n bakalım. f(3) 2log 3 4 2 4 6 dır. Buna göre cevap: E şıkkı 12
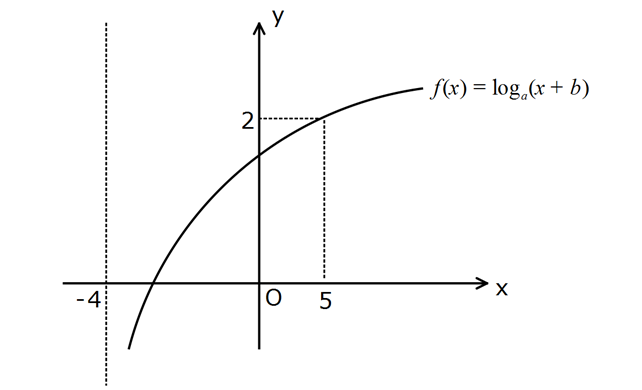
a Yukarıdaki grafik f(x) log (x b) fonksiyonuna aittir. Buna göre, f(77) kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 x 4 değeri log aritmayı ‘ a götürüyorsa logaritmanın içini 0 yapan değer 4 tür. x b 0 : Çözüm a a 2 a 3 3 3 3 4 b 0 b 4 tür. (5,2) noktası da fonkisyonu sağılıyor.Buna göre; 2 log (5 4) 2 log 9 log 3 2 ise a 3 tür. f(x) log (x 4) tür. f(77) log (77 4) log (81) log (34 ) 4 buluruz. 20
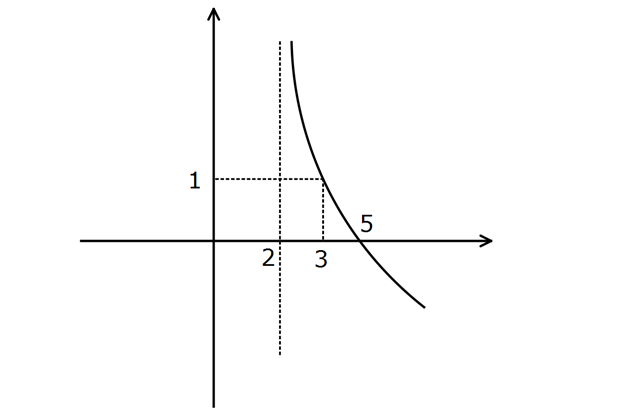
b a, c R ve b R olmak üzere f : (2, ) R f(x) a log (x c) fonksiyonunun grafiği yukarıda ver ilmiştir. Buna göre, f(11) kaçtır? A) 3 B) 1 C) 1 D) 2 E) 3 www.matematikkolay.net b b 0 tanımsı f(x) a log (x c) x 2 değeri log aritmayı tanımsız yapan değerdir. f(x) a log (x c) : Çözüm 1 zlık b b b 0 b b 1 1 3 1 3 2 3 3 2 c 0 c 2 dir. f(x) a log (x 2) f(3) 1 ve f(5) 0 1 a log (3 2) a log 1 1 a 1 dir. 0 1 log (5 2) log 3 1 1 3 b b tür. 3 f(x) 1 log (x 2) dir. f(11) 1 log (11 2) f(11) 1 log 3 1 2log 3 1 1 bulunur. 85
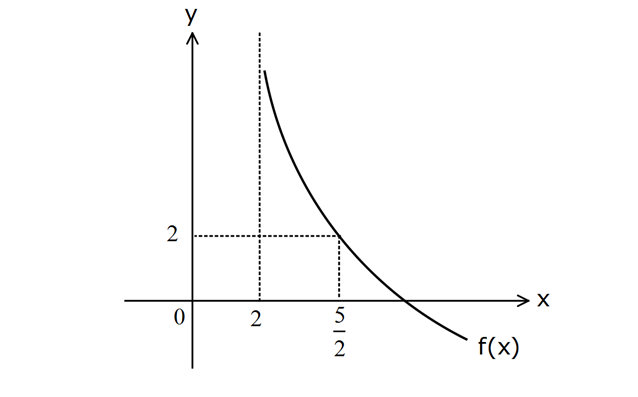
a a Şekilde, f(x) log (x b) fonksiyonunun grafiği veril – miştir. Buna göre, log (2b 6) değeri kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 logaritmanın içi 0 olursa, fonksiyon tanımsız olur. Demek ki x 2 değeri log aritmanın içi : ni 0 Çözüm 1 2 a 2 a a a 1 2 2 1 2 a 2 yapmış. log (x b) 2 b 0 b 2 dir. 5 log (x 2) fonksiyonu , 2 noktasından geçi – 2 5 1 yorsa 2 log 2 2 log 2 2 1 a a 2 a 2 dir. Buna göre; 2 log (2b 6) log 1 2 2 (2.( 2) 6) 1 log (2) 2 buluruz. 1 2 www.matematikkolay.net 103
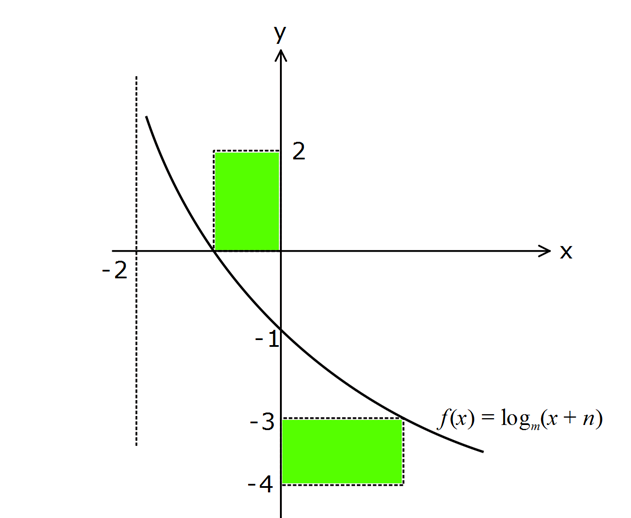
www.matematikkolay.net m Yukarıda f(x) log (x n) fonksiyonunun grafiği verilmiştir. Buna göre, taralı bölg elerin alanları t 2 oplamı kaç br dir? A) 6 B) 8 C) 9 D) 11 E) 12 www.matematikkolay.net m log (x n) x 2 için logaritma tanımsız oluyorsa n 2 dir. x 0 değeri için, log aritmanın değer : Çözüm 1 1 1 m 2 2 i 1 ise; log (0 2) 1 m 2 olmalıdır. Buna göre; log (x 2) ‘nin grafiği çizilmiştir. Üstteki dikdörtgen için, logaritmanın x eksenini kestiği yere ihtiyacımız var. log (x 2) 0 x 2 1 x 1 3 2 1 dir. Bu dikdörtgenin alanı 2.1 2 buluruz. Alttaki dikdörtgen için logaritmayı 3 yapan x değerine ihtiyacımız var. log (x 2) 3 x 2 2 x 6 dır. Bu dikdörtgenin alanı 1.6 6 dır. İki di kdörtgenin alanları toplamı 2 6 8 buluruz. 114
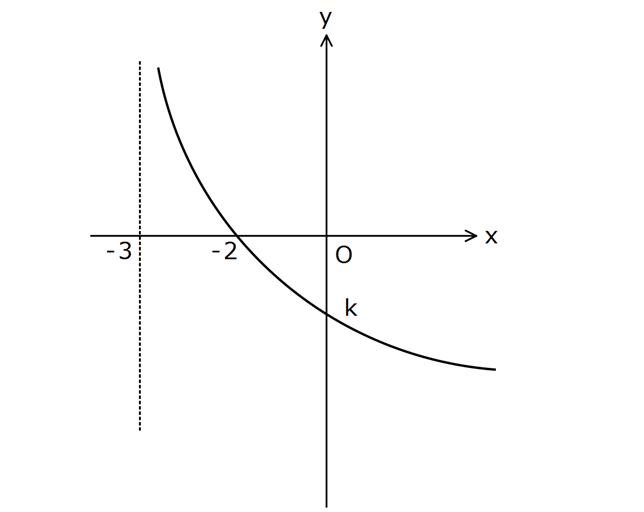
1 3 f(x) log (x n) fonksiyonunun grafiği yukarıda verilmiştir. Buna göre, k n kaçtır? www.matematikkolay.net 1 3 f(x) log (x n) Grafiği incelediğimizde x 3 noktasında tanımsızlık görünüyor.O halde, x 3 : i Çözüm 1 1 3 1 3 1 3 3 3 çin x n 0 dır. 3 n 0 n 3 tür. f(x) log (x 3) tür. x 0 için f(0) k log (0 3) k dır. log 3 k log 3 log 3 1 k 1 dir. k n 1 3 2 bulunur. 129
www.matematikkolay.net 1 Grafikte verilenlere göre, f(14) f (5) toplamı kaçtır? A) 25 B) 49 C) 121 D) 125 E) 225 a a 2 a Grafiğe göre, x 5 için f(x) 2 dir. Buna göre; log 2.5 1 2 log 10 1 2 log 9 2 a 9 : Çözüm 3 3 3 3 3 1 3 5 ise a 3 tür. f x log 2x 1 olur. f 14 log 28 1 log 27 log 3 3 tür. f 5 x ise f x 5 tir. log 2x 1 5 2x 1 3 1 2x 1 243 2x 244 x 122 dir. O halde; f 14 f 5 3 122 125 buluruz. 137

