Soru Sor sayfası kullanılarak Logaritma konusu altında Çarpanlara ayırarak logaritmik denklem çözme ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

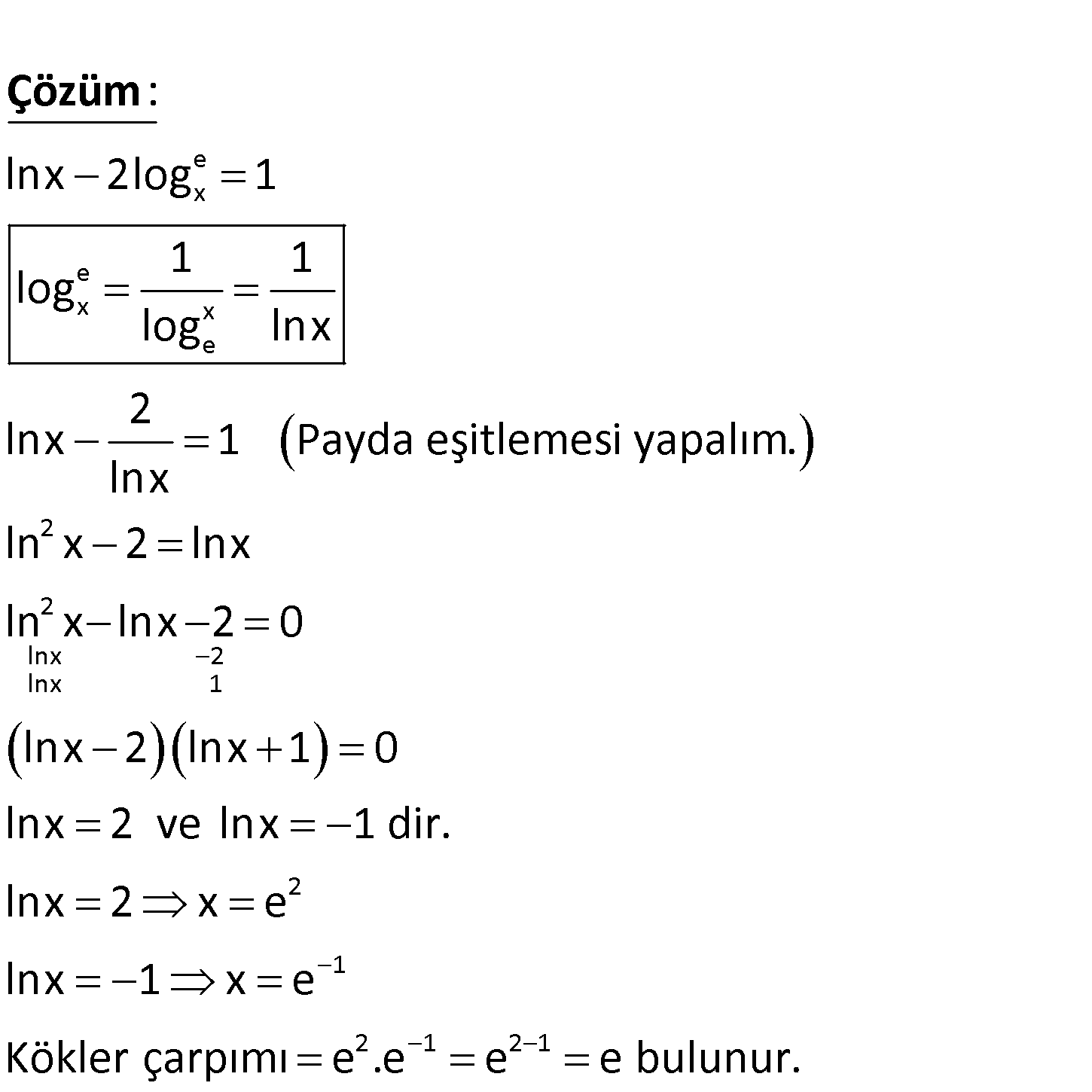
2.SORU
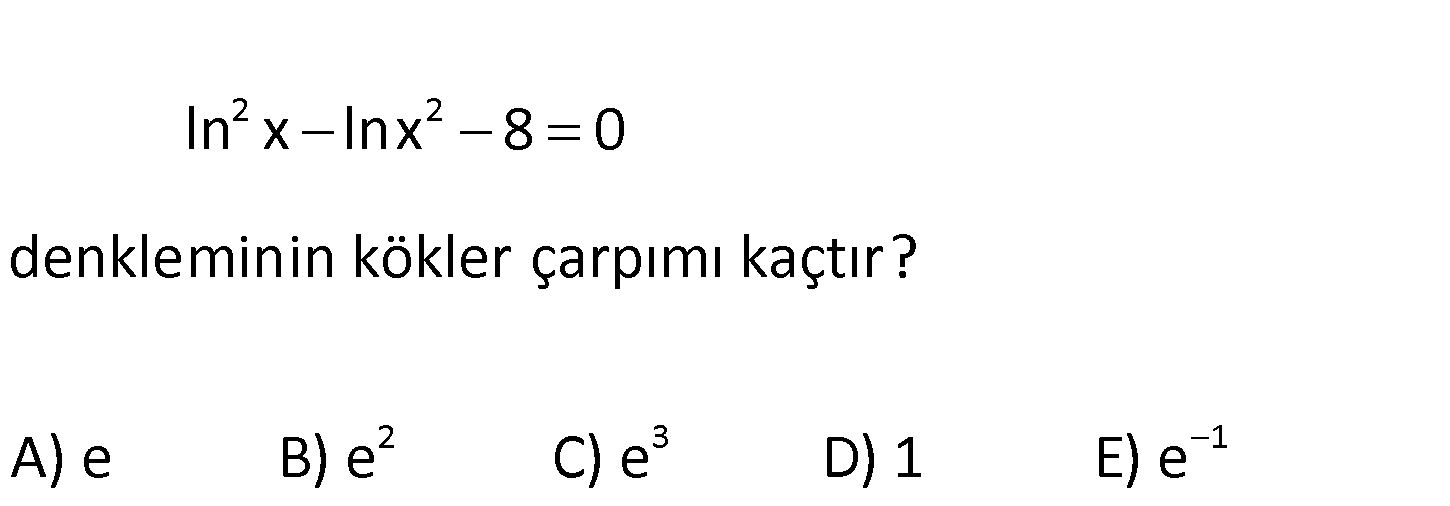

3.SORU
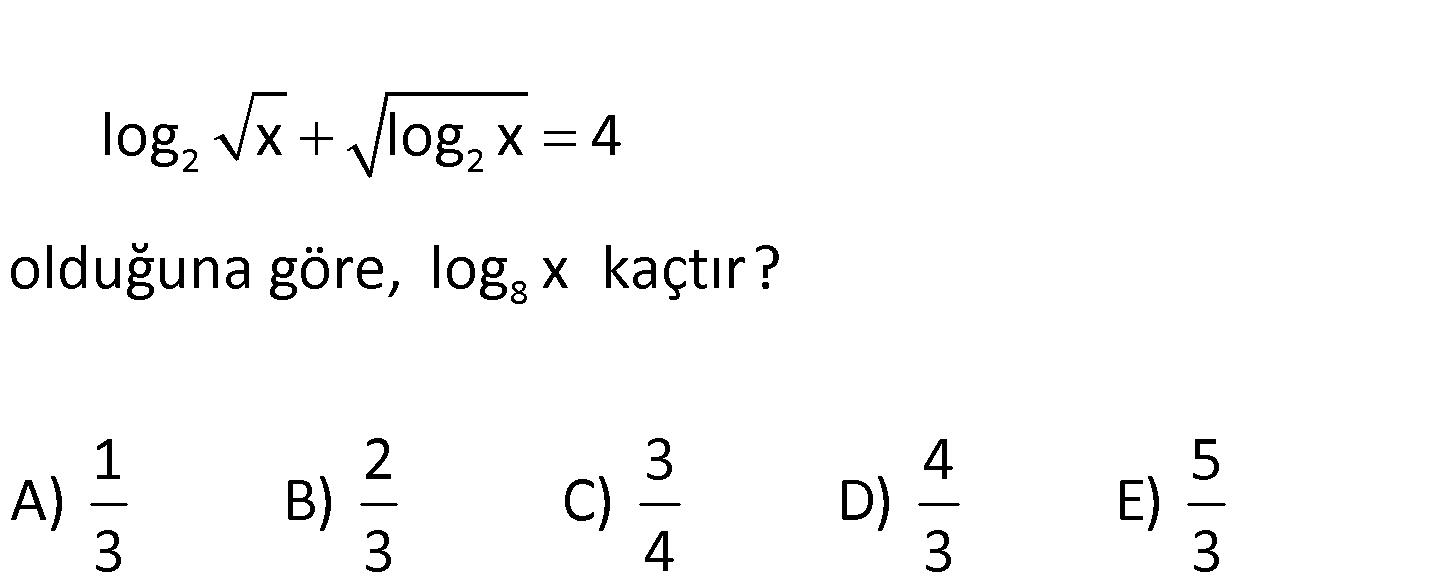

4.SORU
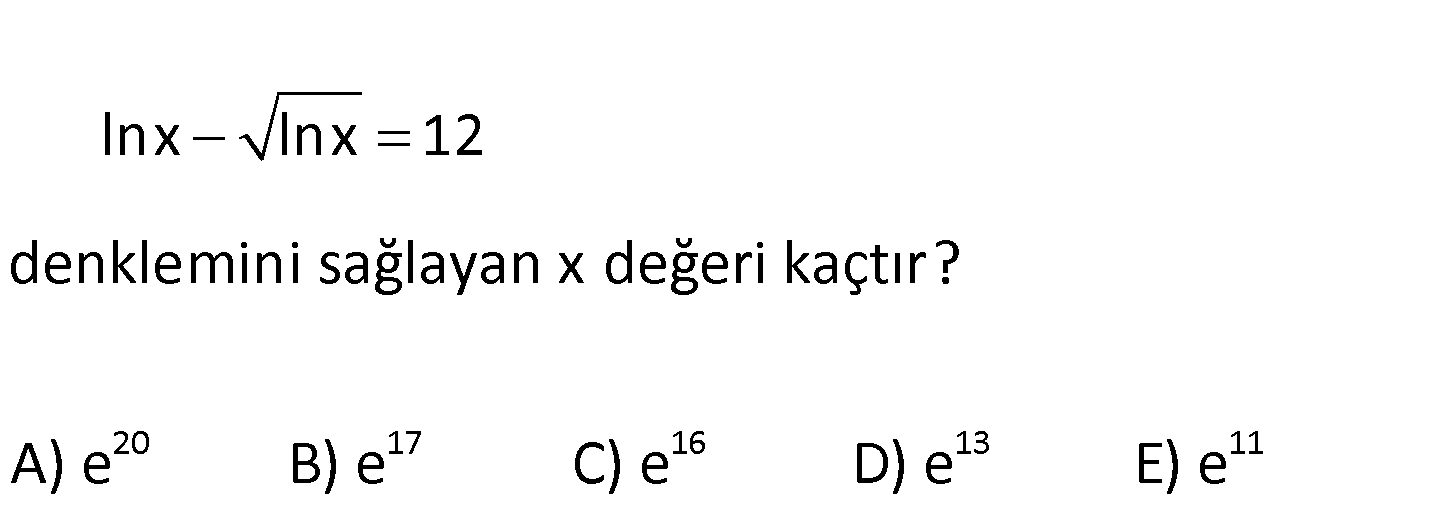
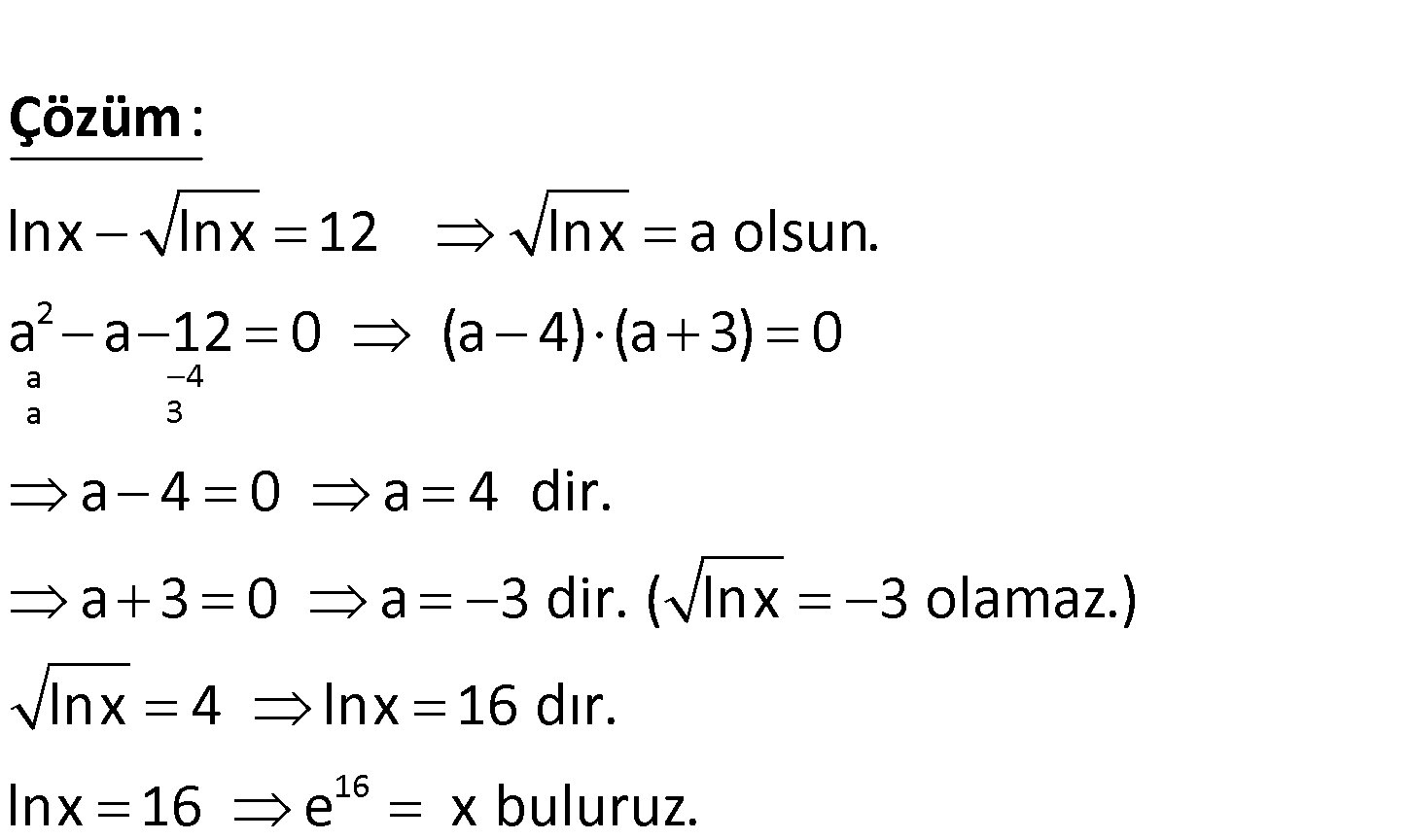
5.SORU
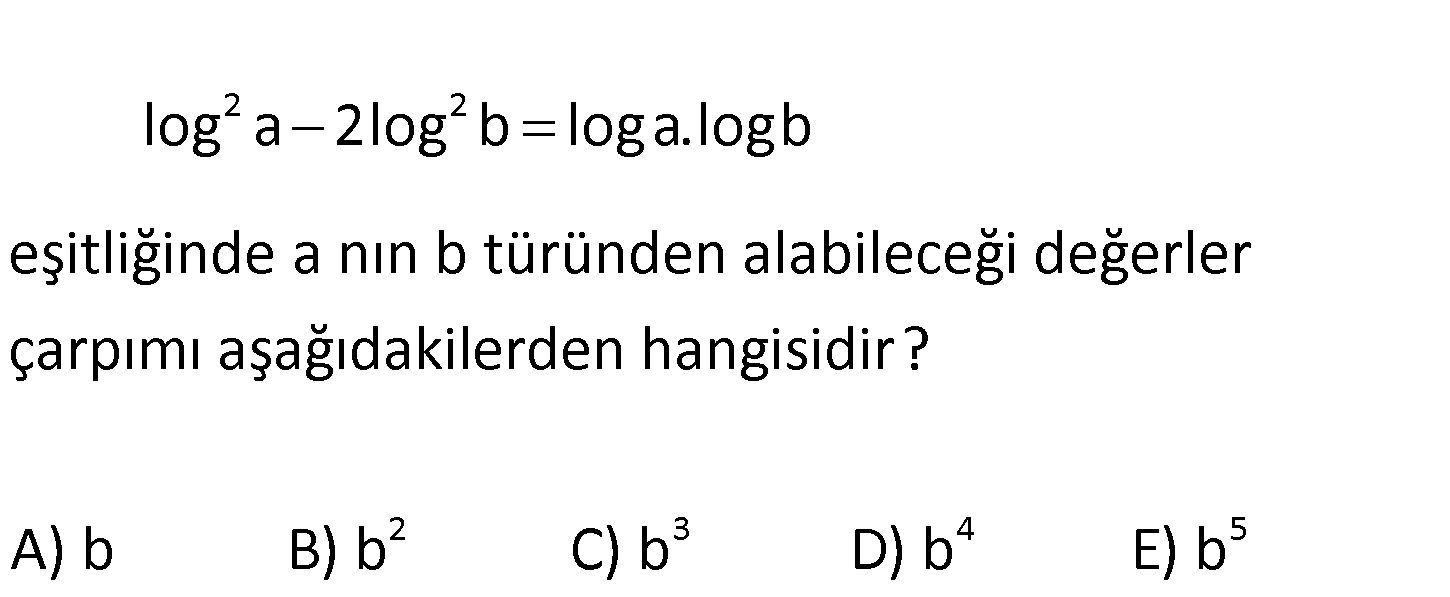

Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
x 3 2 1 2 lnx 2log e 1 denkleminin köklerinin çarpımı kaçtır? A) e B) e C) e D) e E) e www.matematikkolay.net e x e x x e 2 2 lnx lnx lnx 2log 1 1 1 log log lnx 2 lnx 1 Payda eşitlemesi yapalım. lnx ln x 2 lnx ln : x lnx Çözüm 2 1 2 1 2 1 2 1 2 0 lnx 2 lnx 1 0 lnx 2 ve lnx 1 dir. lnx 2 x e lnx 1 x e Kökler çarpımı e .e e e bulunur. 130
2 2 2 3 1 ln x lnx 8 0 denkleminin kökler çarpımı kaçtır? A) e B) e C) e D) 1 E) e www.matematikkolay.net 2 2 2 2 4 2 ln x lnx 8 0 ln x 2lnx 8 0 lnx a olsun. a 2a 8 0 a 4 a 2 0 a 4 ve a 2 dir. lnx 4 ol uğ : d Çözüm 4 2 4 2 2 unda x e olur. lnx 2 olduğunda x e olur. Kökler çarpımı e .e e buluruz. 138
2 2 8 log x log x 4 olduğuna göre, log x kaçtır? 1 2 3 4 5 A) B) C) D) E) 3 3 4 3 3 2 2 1 2 2 2 2 2 2 2 log x log x 4 log x log x 4 1 log x log x 4 her tarafı 2 ile çarpalım. : 2 log x 2 log Çözüm 3 2 2 2 2 0 2 2 2 4 4 4 8 8 2 x 8 log x 2 log x 8 0 çarpanlarına ayıralım. ( log x 4)( log x 2) 0 log x 2 0 log x 2 log x 4 x 2 tür. 4 log x log 2 log 2 buluruz. 3 15
20 17 16 13 11 lnx lnx 12 denklemini sağlayan x değeri kaçtır? A) e B) e C) e D) e E) e 2 a 4 a 3 lnx lnx 12 lnx a olsun. a a 12 0 (a 4) (a 3) 0 a 4 0 a 4 dir. a 3 0 a 3 dir. ( : Çözüm 16 lnx 3 olamaz.) lnx 4 lnx 16 dır. lnx 16 e x buluruz. 51
2 2 log a 2log b loga.logb eşitliğinde a nın b türünden alabileceği değerler çarpımı aşağıdakil 2 3 4 5 erden hangisidir? A) b B) b C) b D) b E) b www.matematikkolay.net 2 2 2 2 loga 2logb loga logb log a 2log b loga.logb log a loga.logb 2log b 0 loga 2logb . lo : ga logb 0 Çözüm 2 2 2 2 2 loga 2logb 0 loga logb 0 a a log 0 1 a b dir. …(1) b b loga logb 0 loga logb 0 1 log(a.b) 0 a.b 1 a dir. … (2) b 1 a değerlerinin çarpımı b b bulunur. b 83

