Soru Sor sayfası kullanılarak Limit konusu altında Grafikten sürekliliğe karar verme ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
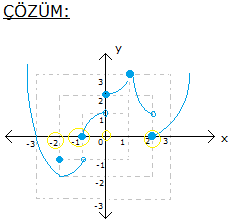
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
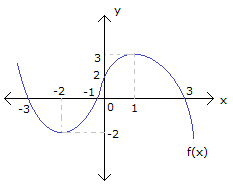
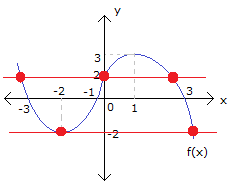
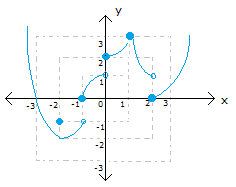
Yukarıda grafiği verilen f fonksiyonu için 5 g(x) fonksiyonu kaç noktada süreksizdir? f(x) 2 A) 6 B) 5 C) 4 D) 3 E) 2 www.matematikkolay.net Çözüm: 5 g(x) f(x) 2 0 olduğu durumlarda f(x) 2 g(x) süreksiz olur. f(x) 2 0 f(x) 2 f(x) 2 veya f(x) 2 dir. Grafiğe bakılırsa f(x) 2 olan 3, x değeri; f(x) 2 olan 2, x değeri var dır. Buna göre g(x) fonksiyonunun 5 noktada süreksiz olduğu bulunur. 14 www.matematikkolay.net Şekikde grafiği verilen y f(x) fonksiyonunun ( , ) aralığında süreksiz olduğu noktalardaki fonksiyon değerlerinin toplamı kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 www.matematikkolay.net Fonskiyonunun limitinin olmadığı veya limiti olmasına rağmen o noktadaki değerinin limitten farklı olduğu noktalarda fonksiyon süreksizdir. Grafikte kopmaların olduğu noktalarda süreksizliği çok rahat görebiliriz. x 2 noktasında fonksiyonun limiti var fakat fonksiyonun 2 noktasındaki değeri limitten farklı x 1 sağdan soldan limitler farklı, yani limit yok. x 0 sağdan soldan limitler farklı,limit yo k x 1 sağdan soldan limitler farklı,limit yok x 2 sağdan soldan limitler farklı,limit yok Bu noktalardaki fonksiyon değerlerini bulalım. x 2 f( 2) 1 x 1 f( 1) 0 x 0 f(0) 2 x 1 f(1) 3 x 2 f(2) 0 1 0 2 3 0 4 bulunur. 72

