Soru Sor sayfası kullanılarak Limit konusu altında Grafikten limit okuma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
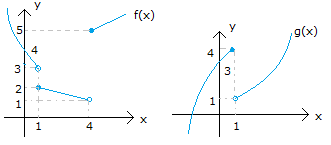


2.SORU
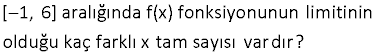

3.SORU


4.SORU
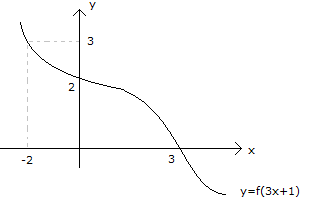
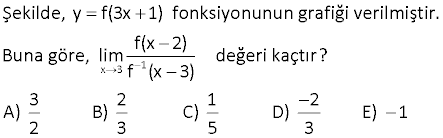

5.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
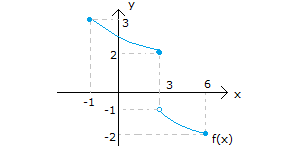
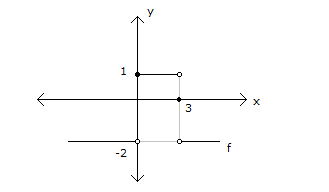
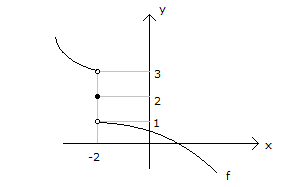
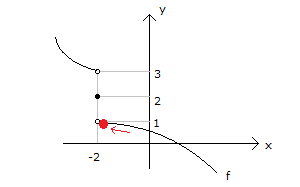
x 0 x 4 x 1 Yukarıdaki şekilde, f(x) ve g(x) fonksiyonlarının gra – fikleri verilmiştir. I. lim (fof)(x) 5 II. lim (gof)(x) 4 III. lim (gog)(x) 1 ifadelerinden hangileri doğrudur? A) Yalnız I B) Yalnız II C) Yalnız III D) I ve III E) I, II ve III www.matematikkolay.net x 0 Çözüm: I.öncülü inceleyelim. lim(fof)(x) 5 f(f(0 )) f fonksiyonu,0’ın solundaki değerler için 4′ ten fazla değerler alıp, en sonunda 4’e yaklaşıyor. f(0 ) 4 dır. f(f(0 )) f(4 ) 4’ün sağındaki d x 4 eğerler için , 5′ ten büyük değerler alıp 5’e yaklaşıyor. I. öncül doğrudur. II.öncülü inceleyelim. lim(gof)(x) 4 g(f(4 )) f fonksiyonu,4’ün solundaki değerler için 1’den fazla değerler alıp, en x 4 sonunda 1’e yaklaşıyor. f(4 ) 1 dır. g(f(4 )) g(1 ) g fonksiyonu ise; 1’in sağındaki değerler için , 1’den büyük değerler alıp 1’e yaklaşıyor. lim(gof)(x) 1 II. öncül yanlıştır. III.öncülü i x 1 nceleyelim. lim(gog)(x) 1 g(g(1 )) g fonksiyonu,1’in sağındaki değerler için 1’den büyük değerler alıp, en sonunda 1’e yaklaşıyor. g(1 ) 1 dır. g(g(1 )) g(1 ) Yine,1’in sağındaki değerler için x 1 1’den büyük değerler alıp, en sonunda 1’e yaklaşıyor. lim(gog)(x) 1 III. öncül doğrudur. 47 www.matematikkolay.net [ 1, 6] aralığında f(x) fonksiyonunun limitinin olduğu kaç farklı x tam sayısı var dır? Çözüm: Bir fonksiyonun limitinin olması için; sağdan ve soldan aynı değere gelmesi gerekir. O noktadaki değeri önemli değildir. (Fonskiyonun uç noktalarında ise tek taraf tan limitinin olması yeterlidir.) x 1 için Sağdan yaklaşılınca limiti 3 olur. Uç nokta olduğu için soldan bakmaya gerek yok . (Limit var.) x 0 için Sağdan ve soldan yaklaşılınca aynı değere ulaşılacak. (Limit var.) Zaten fonksiyo n grafiğinde bir atlama zıplama yoksa, gözümüz kapalı limiti var diye – biliriz. x 1 için Atlama, zıplama yok . Limit var x 2 için Atlama, zıplama yok . Limit var x 3 için Sağdan yaklaşınca 1, soldan yaklaşınca 2 farklı değerler (Limit yok) x 4 için Atlama, zıplama yok . Limit var x 5 için Atlama, zıplama yok . Limit var x 6 için Soldan yaklaşılınca limiti 2 olur. Uç nokta olduğu için sağdan bakmaya gerek yok . (Limit var.) Limit olan noktalar 1,0,1,2,4,5,6 (3 hariç) 7 tane buluruz. 48 www.matematikkolay.net 0 0 0 0 x x f fonksiyonu yardımıyla g fonksiyonu, her x R için g(x ) f(x ) lim f(x) biçiminde tanımlanıyor. Buna göre, (gof)(3) değeri kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 0 x 0 x 0 Çözüm: gof(3) g(f(3)) tür. f(3) 0 dır. (f fonksiyonununda 3 değerinin karşılığı 0 dır.) g(f(3)) g(0) Bize verilen g fonksiyonunun tanımında yazalım. g(0) f(0) lim f(x) f(0) 1 dir. lim f(x) f fonksiy x 0 x 0 onunda 0’a soldan yaklaşmak 0’ın negatif tarafından yaklaşmaktır.Buna göre lim f(x) 2 dir. g(0) f(0) lim f(x) 1 ( 2) 1 bulunur. 50 www.matematikkolay.net x 3 1 Şekilde, y f(3x 1) fonksiyonunun grafiği verilmiştir. f(x 2) Buna göre, lim değeri kaçtır? f (x 3) 3 2 1 2 A) B) C) D) E) 1 2 3 5 3 x 3 1 1 1 1 0 1 Çözüm: f(x 2) f(3 2) f(1) lim dır. f (x 3) f (3 3) f (0) f(1) ve f (0)’a ihtiyacımız var. f(3x 1)’in grafiği var elimizde. x 0 için f(3x 1) 2 olduğundan f(1) 2 dir. f (0)’ı da bulalım; f(3x 1) 1 3 1 0 olduğunda x 3 ise; f(3x 1) 0 f(10) 0 dır. f (0) 10 dur. Buna göre; sorunun cevabını f(1) 2 1 buluruz. f (0) 10 5 52 www.matematikkolay.net x 2 Yukarıdaki şekilde, f fonksiyonun grafiği verilmiştir. g(x) x 1 f(x) olduğuna göre, lim g(x) değeri kaçtır? www.matematikkolay.net x 2 x 2 x 2 x 2 x 2 x 2 Çözüm: lim g(x) lim |x 1|.f(x) lim |x 1| lim f(x) | 2 1|. lim f(x) 1. lim f(x) f(x) fonksiyonunda; x 2’ye sağdan yaklaşınca, 1’e doğru yaklaşıyoruz. 01.Oca 1 buluruz. 53


1 sorunun 3. Onculu yanlis cozulmus
Kontrol ettik ama hata göremedik.