Soru Sor sayfası kullanılarak Kümeler konusu altında Üç kümeli problemler ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


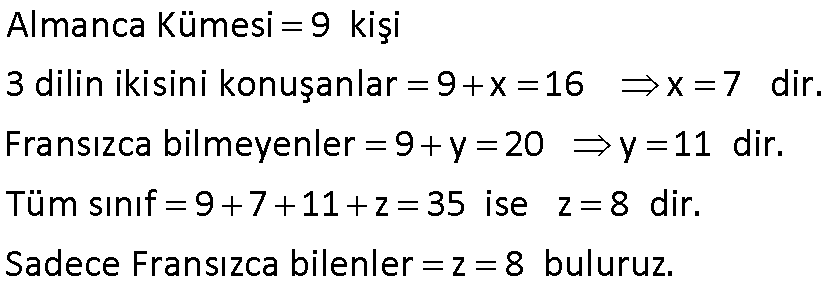
2.SORU


3.SORU


4.SORU


5.SORU



6.SORU


7.SORU



8.SORU

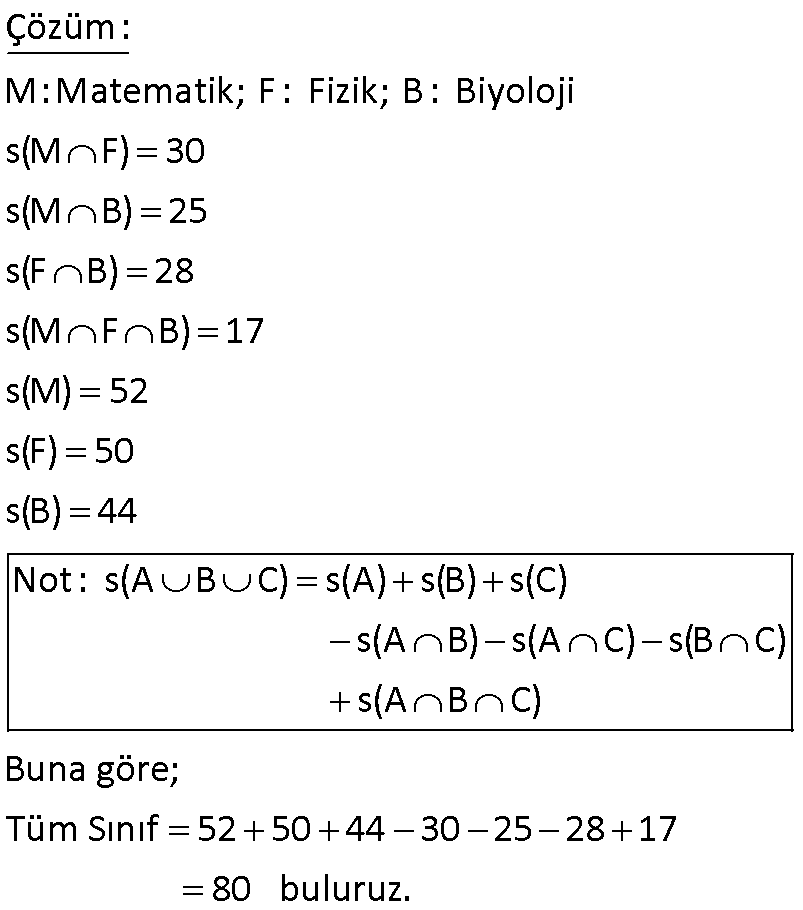
9.SORU

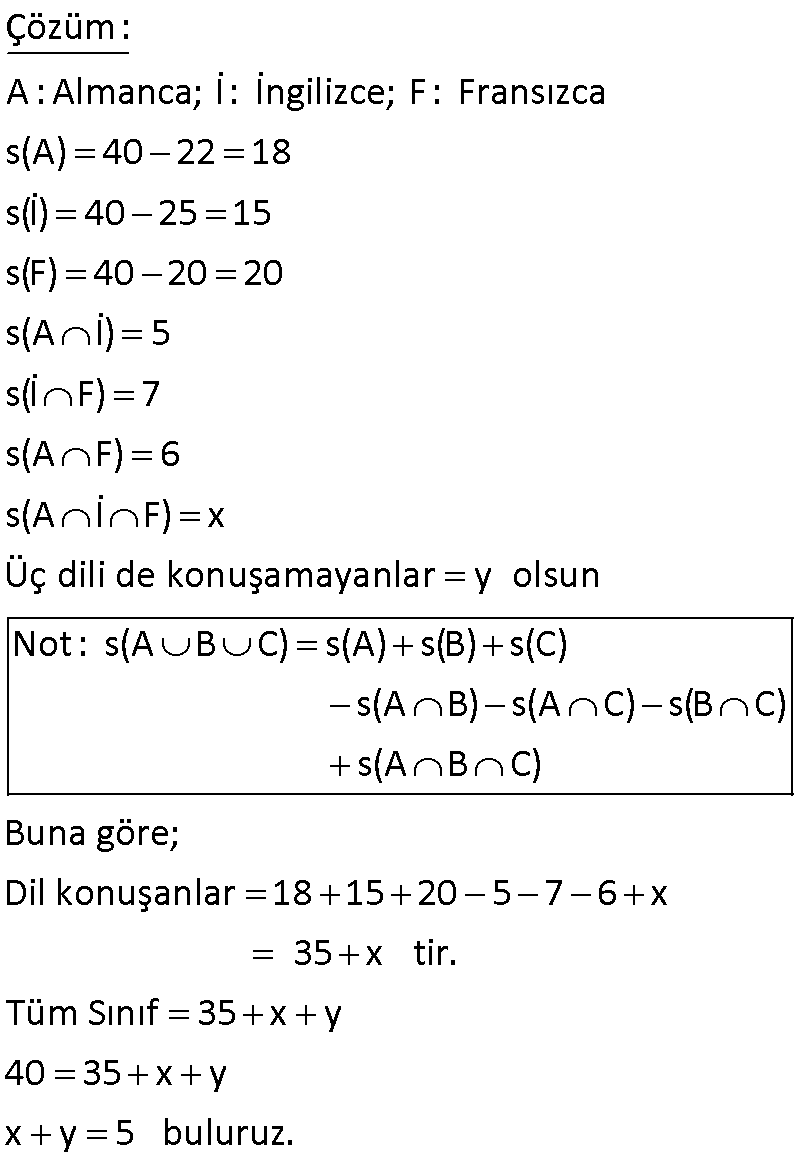
10.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
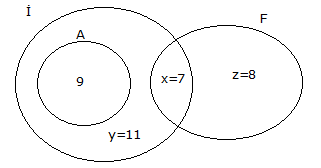
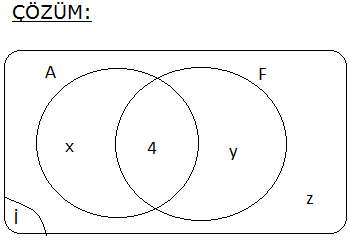
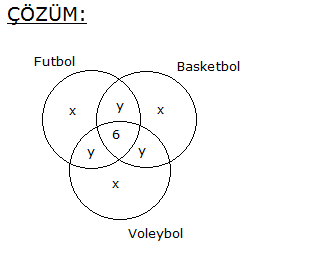
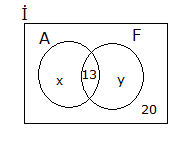
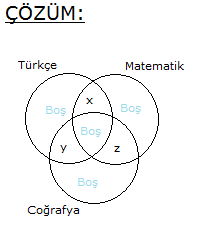
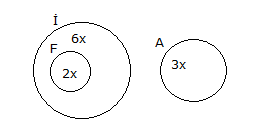
www.matematikkolay.net Almanca, İngilizce, Fransızca dillerinden en az birini bilenlerin hepsi İngilizce de bilmekte Fransızca bilme – mektedir. Bu sınıfta Almanca bilenler 9, bu üç dilin ikisini bilenler 16, Fransızca bilmeyenler 20 kişidir. Bu sınıfta sadece Fransızca bilenler kaç kişidir? A) 6 B) 7 C) 8 D) 9 E) 9 Çözüm: Almanca bilenler, aynı zamanda İngilizce biliyorsa Almanca bilenler, İngilizce bilenlerin bir alt kümesidir. Ve bunların hiç biri Fransızca bilmiyorsa, kesişim kümeleri yoktur. Buna göre kümeleri çizelim. Almanca Kümesi 9 kişi 3 dilin ikisini konuşanlar 9 x 16 x 7 dir. Fransızca bilmeyenler 9 y 20 y 11 dir. Tüm sınıf 9 7 11 z 35 ise z 8 dir. Sadece Fransızca bilenler z 8 buluruz. 11 www.matematikkolay.net 24 kişilik bir grupta herkes İngilizce bilmektedir. Bu grupta Almanca bilmeyen 16 kişi, Fransızca bilmeyen 14 kişi bulunup her üç dili de bilen 4 kişi varsa en az iki dili bilen kaç kişi var dır? A) 7 B) 8 C) 9 D) 10 E) 11 20 Herkes İngilizce bildiğine göre; x y z 4 24 x y z 20 dir. Almanca bilmeyen 16 kişi olduğuna göre; y z 16 dır. Fransızca bilmeyen 14 kişi olduğuna göre; x z 14 tür. x z y z 16 14 30 x y z z 30 z 10 dur. En az iki dil bilenler; 24 10 14 bulunur. www.matematikkolay.net 34 Ana dili Türkçe olan 42 kişilik bir toplulukta 3 dil bilenlerin sayısı 2 dil bilenlerin sayısından 2 fazla, hiç yabancı dil bilmeyenlerin sayısının 3 katından 6 eksiktir. Bu toplulukta 4 dil bilen olmadığına göre, en çok iki dil bilen kaç kişi var dır? A) 21 B) 22 C) 24 D) 25 E) 27 Çözüm: Üç dil bilenler : x iki dil bilenler : y hiç yabancı dil bilmeyenler : z en çok iki dil bilenler : y z x y z 42 x y 2 x 3z 6 y 2 3z 6 y 3z 8 Şimdi ilk denklemde hepsini z cinsinden yazalım. 3z 6 3z 8 z 42 7 z 14 42 7z 56 z 8 dir. y 3z 8 3.8 8 24 8 16 dır. y z 16 8 24 buluruz. 40 www.matematikkolay.net Futbol, basketbol ve voleybol oyunlarından en az birini oynayanlardan oluşan 48 kişilik bir grupta; her üç oyunu da oynayanların sayısı 6, sadece futbol, sadece basketbol ve sadece voleybol oynayanlardan herhangi ikisini oynayanların sayıları da birbirine eşittir. Buna göre, futbol oynayanların sayısı en az kaçtır? A) 14 B) 16 C) 18 D) 21 E) 24 www.matematikkolay.net Sadece birini oynayanlara x diyelim. İki oyun oynayanlara da y diyelim. Üç oyun oynayanlar 6 kişi denmiş. Toplamları 48 ise; 3x 3y 6 48 3x 3y 42 x y 14 tür. Küme şeklinden de a 14 nlaşılacağı üzere; Futbol oynayanlar x y y 6 20 y dir. En az olması için y 1 seçelim. 21 buluruz. 72 40 kişilik bir grupta herkes İngilizce konuşabiliyor. 13 kişi Almanca ve Fransızca biliyor. Yalnız İngilizce konuşabilen 20 kişi olduğuna göre Almanca ve Fransızcadan yalnız birini bilen kaç kişi vardır? www.matematikkolay.net Çözüm: Grupta herkes İngilizce biliyor ise Evrensel küme İngilizce bilenler olur. Almanca veya Fransızca bilen insanların oluşturduğu küme bu kümenin alt kümesi olur.Şimdi verilenleri kümeye yerleştirelim. Yalnız Almanca bilenler x kişi olsun. Yalnız Fransızca bilenler y kişi olsun. Bu dillerden yalnız birini bilenler x y olur. Şimdi kümelerin içindeki tüm sayıları toplayıp, 40’a eşitleyelim. x 13 y 20 40 x y 40 20 13 x y 7 bulunur. 75 www.matematikkolay.net Türkçe, Matematik ve Coğrafya derslerinden herhangi ikisinin seçildiği bir toplulukta Türkçe dersini 24, Matematik dersini 21, Coğrafya dersini ise 19 kişi seçmiştir. Türkçe dersini seçmeyen kaç kişi vardır? A) 8 B) 10 C) 11 D) 12 E) 13 24 Türkçe x y 24 Matematik x z 21 Coğrafya y z 19 taraf tarafa toplarsak 2x 2y 2z 64 2 x y z 64 x y z 32 di r. z 8 buluruz. (Türkçe dersini seçmeyenler) www.matematikkolay.net 79 www.matematikkolay.net Futbol, basketbol veya voleybol oyunlarından en az birini oynayanlardan oluşan 40 kişilik bir spor – cu kafilesinde futbol oynayanlar başka oyun oynamamaktadır. Bu kafilede yalnız basketbol oynayanların sayısı yalnız voleybol oynayanların sayısına eşit ve futbol oynayanların sayısının yarısıdır. Bu kafilede bu oyunlardan ikisini oynayan 8 kişi olduğuna göre, basketbol veya voleybol oynayan kaç kişi vardır? A) 36 B) 35 C) 32 D) 24 E) 16 Soruda verilenlere yukarıdaki gibi kümeleri doldurabiliriz. Hepsinin toplamı 40 ise; 4a 8 40 4a 32 a 8 dir. Basketbol veya Voleybol 2a 8 16 8 24 buluruz. www.matematikkolay.net 82 www.matematikkolay.net Bir okulda 30 öğrenci, Matematik ve Fizik, 25 öğren – ci Matematik ve Biyoloji, 28 öğrenci Fizik ve Biyo – lojiden, 17 öğrencide her üç dersten sınava girmek – tedir. Matematik sınavına 52, Fizik sınavına 50, Biyoloji sınavına 44 öğrenci girdiğine göre, tüm sınavlara katılan kaç öğrenci var dır? A) 70 B) 80 C) 82 D) 88 E) 90 Çözüm: M:Matematik; F: Fizik; B: Biyoloji s(M F) 30 s(M B) 25 s(F B) 28 s(M F B) 17 s(M) 52 s(F) 50 s(B) 44 Not : s(A B C) s(A) s(B) s(C) s(A B) s(A C) s(B C) s(A B C) Buna göre; Tüm Sınıf 52 50 44 30 25 28 17 80 buluruz. 84 www.matematikkolay.net 40 kişilik bir sınıfta, Almanca konuşmayanlar 22, İngilizce konuşamayanlar 25, Fransızca konuşama – yanlar 20 kişidir. Almanca ve İngilizce konuşabilenler 5, İngilizce ve Fransızca konuşabilenler 7, Almanca ve Fransızca konuşabilenler 6 kişi olduğuna göre, bu sınıfta üç dili konuşabilenler ile bu üç dili konuşamayanların sayısının toplamı kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 www.matematikkolay.net Çözüm: A: Almanca; İ: İngilizce; F : Fransızca s(A) 40 22 18 s(İ) 40 25 15 s(F) 40 20 20 s(A İ) 5 s(İ F) 7 s(A F) 6 s(A İ F) x Üç dili de konuşamayanlar y olsun Not : s(A B C) s(A) s(B) s(C) s(A B) s(A C) s(B C) s(A B C) Buna göre; Dil konuşanlar 18 15 20 5 7 6 x 35 x tir. Tüm Sınıf 35 x y 40 35 x y x y 5 buluruz. 85 İngilizce, Fransızca veya Almanca dillerinden en az birini bilenlerin oluşturduğu bir toplulukta; Fransızca bilenlerin hepsi İngilizce bilmekte, Almanca bilme – mektedir. Yalnız İngilizce bilenlerin sayısı; Almanca bilenlerin sayısının 2 katına, Fransızca bilenlerin sayısının 3 katına eşittir. A) 8 B) 9 C) 10 D) 11 E) 12 Çözüm: Fransızca bilenlerin hepsi İngilizce biliyorsa, F kümesi İ kümesinin alt kümesidir. Fransızca bilenler Almanca bilmiyorsa, F A 0 dır. Yalnız İngilizce bilenlere 6x dersek, Almanca bilenler 3x, Frans ızca bilenler 2x olur. Bunların toplamı, topluluktaki kişi sayısını verir. 2x 3x 6x 11x tir. En az olması için x 1 olsun. 11 buluruz. www.matematikkolay.net 87

