Soru Sor sayfası kullanılarak Kümeler konusu altında Eşitlikler verilen üç kümeli sorular ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

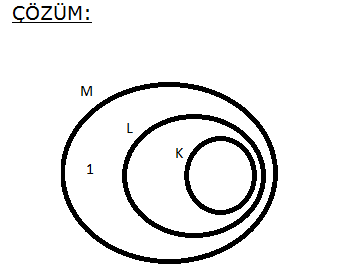

3.SORU

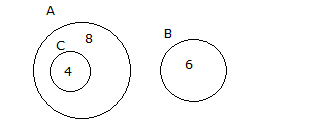

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net A, B ve C aynı evrensel kümenin alt kümeleridir. s(A) s(C’) 10 , s(A’) s(C) 12 ise s(B) s(B’) toplamı kaçtır? A) 9 B) 10 C) 11 D) 12 E) 13 s(E) s(E) Çözüm: Not : Bir küme ile tümleyeninin toplamı evrensel kümeye eşittir. s(A) s(C’) 10 s(A’) s(C) 12 s(A) s(A’) s(C) s(C’) 22 2s(E) 22 s(E) 11 dir. s(B) s(B’) s(E) 11 b uluruz. 27 K, L ve M kümeleri için aşağıdaki bilgiler veriliyor. I. K L ve L M dir. II. L M III. s(K) s(L) s(M) 17 Buna göre boş kümeden farklı K, L ve M kümeleri için, L kümesinin 3 elemanlı alt küme sayısı e n çok kaçtır? A) 20 B) 35 C) 56 D) 64 E) 84 www.matematikkolay.net L M ise s(M L) 1 olmalıdır. (en az) K L M 17 K L L 1 17 K 2L 16 2L 16 K K L 8 2 L en fazla 7 olabilir. 7 7.6.5 3 elemanlı alt küme sayısı 35 tir. 3 3.2.1 50 www.matematikkolay.net A, B ve C kümeleri aynı evrensel kümenin birer alt kümesidir. s(A B) s(A) s(B) s(B C) s(B) s(A C) 4 s(A’) s(A’ C’) s(A) 2s(B) 3s(C ) olduğuna göre, s[A (B C)] kaçtır? A) 6 B) 8 C) 10 D) 12 E) 15 Çözüm: s(A’) s(A’ C’) iki tarafın da değilini alalım. s(A) s(A C) olur. Demek ki C kümesi, A’nın alt kümesidir. s(A C) 4 ise, s(C) 4 tür. s(B C) s(B) ise B ve C kümelerinin kesişimleri boş kümedir. 4 s(A B) s(A) s(B) ise A ve B kümelerinin kesi – şimi de boş kümedir. s(A) 2s(B) 3s(C) s(A) 12 ve s(B) 6 dır. O halde; s[A (B C)] A ile B’nin ortak bir elemenı olmadığı için s(A C)’ yi bulmamız ye terlidir. s(A C) 8 buluruz. www.matematikkolay.net 86

