Soru Sor sayfası kullanılarak Kümeler konusu altında Eşitlikler verilen iki kümeli sorular ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
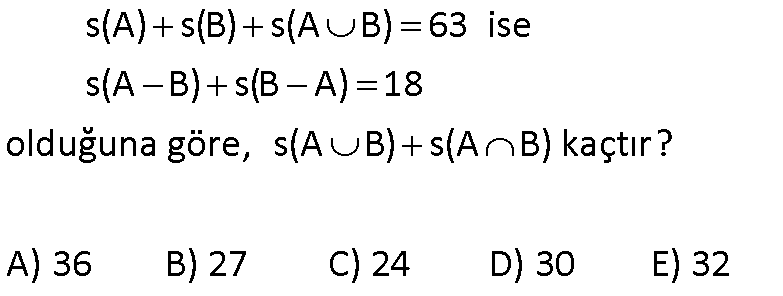
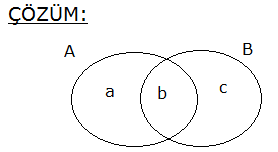

2.SORU


3.SORU

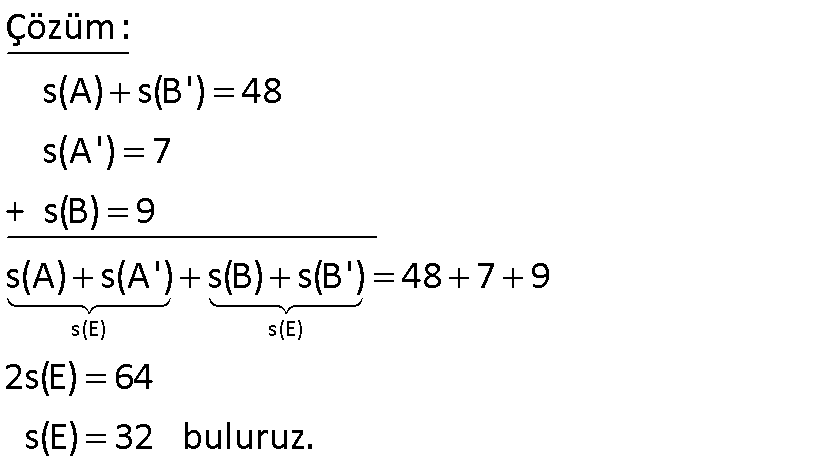
4.SORU

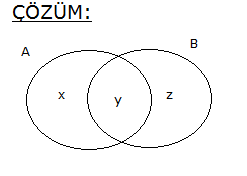

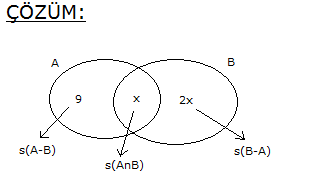
5.SORU
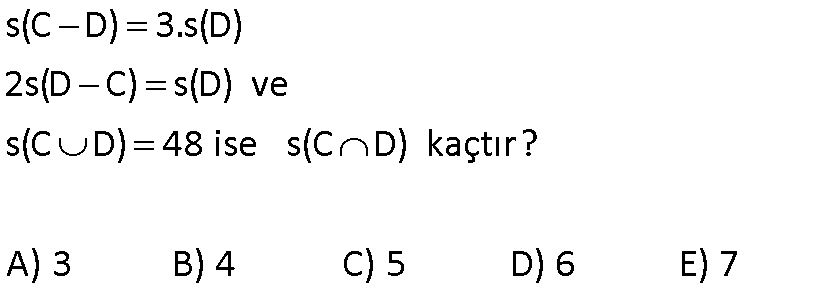
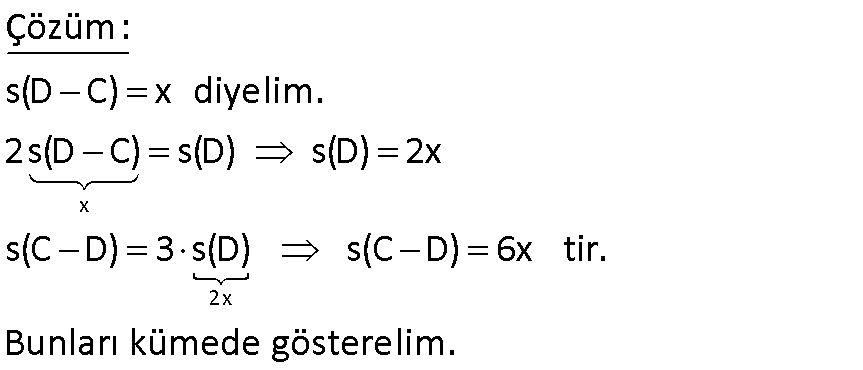
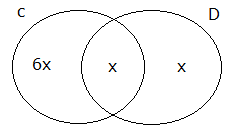

6.SORU

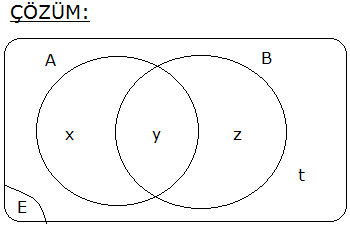
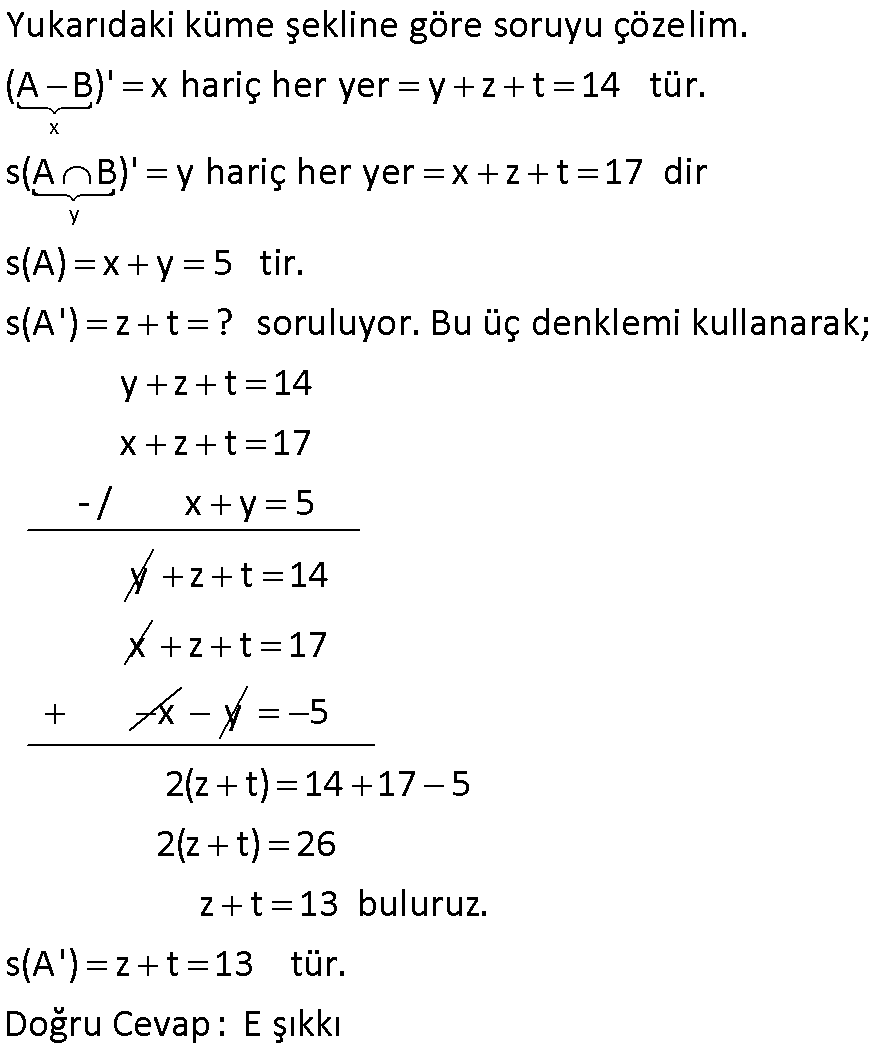
7.SORU
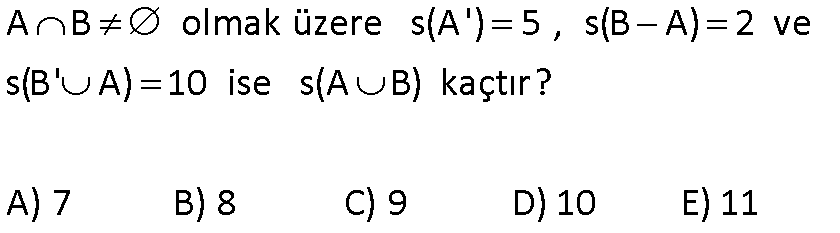
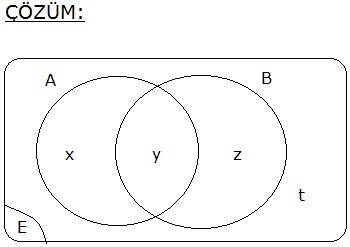

8.SORU
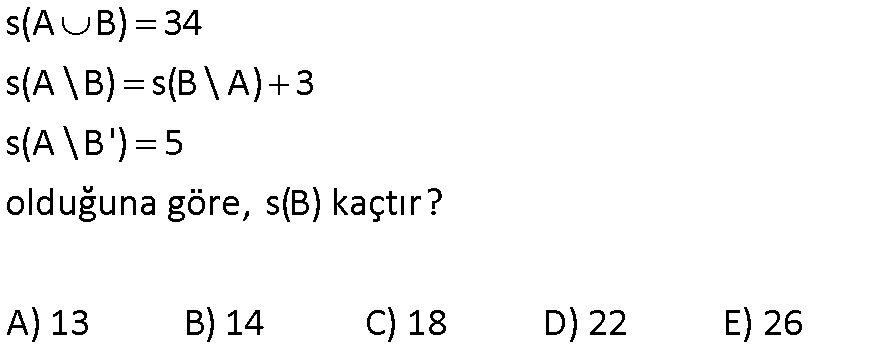

9.SORU

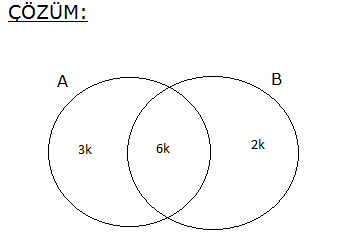
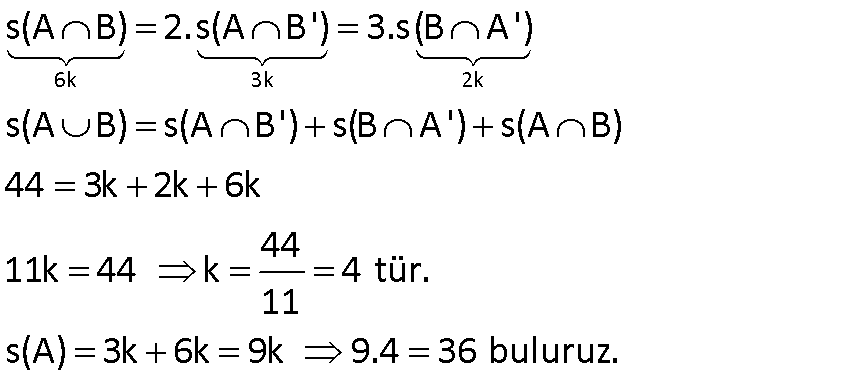
10.SORU


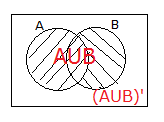
11.SORU
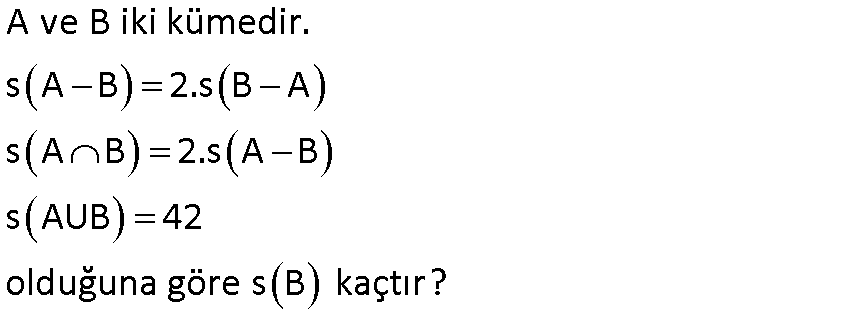
12.SORU


13.SORU
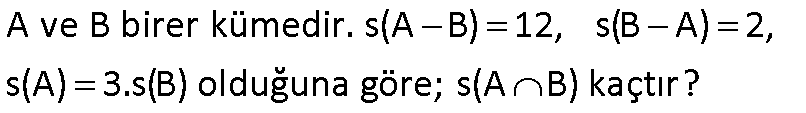

14.SORU

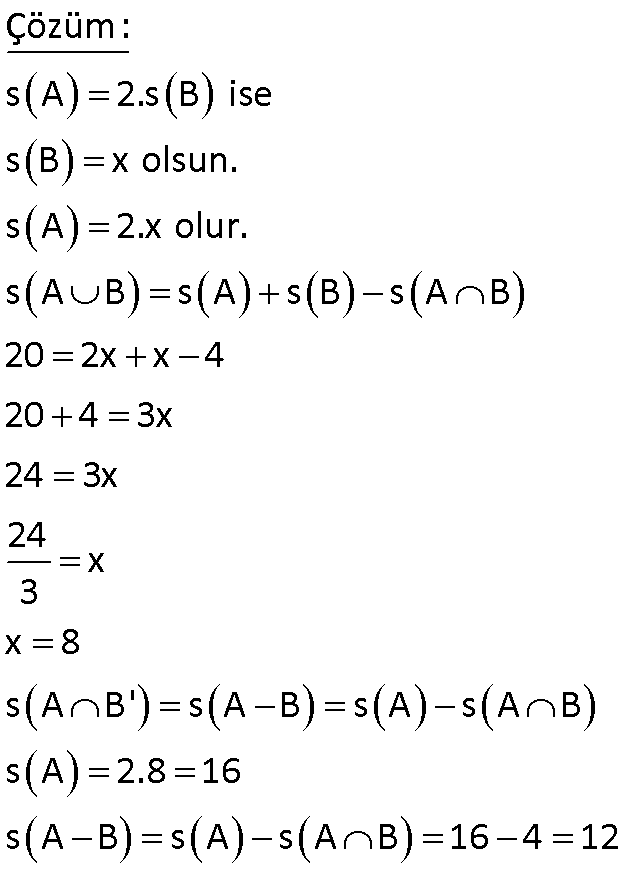
15.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
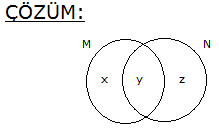
s(A) s(B) s(A B) 63 ise s(A B) s(B A) 18 olduğuna göre, s(A B) s(A B) kaçtır? A) 36 B) 27 C) 24 D) 30 E) 32 36 s(A) s(B) s(A B) 63 ise a b b c a b c 63 2a 3b 2c 63 tür. (I) s(A B) s(B A) 18 a c 18 (II) I. eşitliğe tekrar bakalım, 2a 3b 2c 63 2a 2c 3b 63 3b=63 36 3b 27 b 9 dur. s(A 18 18 B) s(A B) ? a b c b ? a 2b c ? a c 2b 36 buluruz. www.matematikkolay.net 2 \M) 5. \N) o Kesişimleri lduğuna gör boş küme olmayan M ve e, N kümesi en az kaç N kümeleri için; s(N) 4.s(M) s(N s(M A) 12 B) 16 C) 18 D) 20 E) 24 elemanlıdır ? (ÖSS 2003) 5x s(N) 4.s(M) (z y) 4(x y) dir. s(N s(M z 5x Bunu ilk eşitlikte z’nin yerine yazalım. (z y) 4(x y) 5x y 4x 4y x 3y buluruz. x y tür. y’nin tam sayı \ o M) 5. \N) labilmesi için x en az 3 3 olmalıdır. x 3 s(N) y z 5x 5.3 1 15 16 buluruz. 3 3 www.matematikkolay.net 3 A ve B, E evrensel kümesinin alt kümeleri olmak üzere s(A) s(B’) 48 , s(A’) 7 , s(B) 9 ise evrensel kümenin eleman sayısı kaçtır? A) 22 B) 28 C) 32 D) 56 E) 64 s(E) s(E) Çözüm: s(A) s(B’) 48 s(A’) 7 + s(B) 9 s(A) s(A’) s(B) s(B’) 48 7 9 2s(E) 64 s(E) 32 buluruz. 5 A ve B boş olmayan iki kümedir. s(A B) 3.s(B A) s(B) 2.s(A) 13 olduğuna göre s(A B) kaçtır ? A) 6 B) 7 C) 8 D) 9 E) 10 www.matematikkolay.net s(A B) 3.s(B A) ise x 3z dir. s(B) 2.s(A) 13 ise y z 2.(x y) 13 y z 2x 2y 13 z 2x 3y 13 z 6z 3y 13 7z 3y 13 y ve z tam sayı olması gerektiği için z 1 ve y 2 olduğunda eşitlik sağlanır. Bu durumda da x 3z 3 tür. s(A B) x y z 3 2 1 6 buluruz. 9 s(C D) 3.s(D) 2s(D C) s(D) ve s(C D) 48 ise s(C D) kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 www.matematikkolay.net x 2x Çözüm: s(D C) x diyelim. 2s(D C) s(D) s(D) 2x s(C D) 3 s(D) s(C D) 6x tir. Bunları kümede gösterelim. s(C D) 48 ise 6x x x 48 8x 48 x 6 dır. Buna göre; s(C D) x 6 buluruz. Doğru Cevap : D şıkkı 18 A ve B aynı evrensel kümenin alt kümeleridir. s(A B)’ 14 s(A B)’ 17 s(A) 5 olduğuna göre, s(A ‘) kaçtır ? A) 4 B) 5 C) 6 D) 8 E) 13 www.matematikkolay.net x y Yukarıdaki küme şekline göre soruyu çözelim. (A B)’ x hariç her yer y z t 14 tür. s(A B)’ y hariç her yer x z t 17 dir s(A) x y 5 tir. s(A’) z t ? soruluyor. Bu üç denklemi kullanarak; y z t 14 x z t 17 – / x y 5 y z t 14 x z t 17 x y 5 2(z t) 14 17 5 2(z t) 26 z t 13 buluruz. s(A’) z t 13 tür. Doğru Cevap : E şıkkı www.matematikkolay.net 20 A B olmak üzere s(A’) 5 , s(B A) 2 ve s(B’ A) 10 ise s(A B) kaçtır? A) 7 B) 8 C) 9 D) 10 E) 11 www.matematikkolay.net x t x y s(A’) z t 5 tir. s(B A) z 2 s(B’ A ) x y t 10 s(A B) x y z ? z t 5 2 t 5 t 3 tür. x y t 10 x y 3 10 x y 7 dir. x y z 7 2 9 buluruz. 31 s(A B) 34 s(A ) s(B ) 3 s(A ) 5 olduğuna göre, s(B) kaçtır? A) 13 B) 14 C) 18 D) 22 E \B \ ) 26 A B’ \ www.matematikkolay.net x 3 x Çözüm: s(A B’) s(A (B’)’) s(A B) 5 tir. s(A B) s(A B) s(B ) (A B) 34 x 3 x 5 34 2x 8 26 2x x 13 tür. s(B) s(B ) s(A B) s(B) 13 5 s(B) 18 bu \ \ \ A \ A luruz. 42 A E ve B E olmak üzere, s(A B) 2.s(A B’) 3.s(B A’) s(A B) 44 olduğuna göre, s(A) kaçtır? A) 24 B) 28 C) 32 D) 34 E) 36 www.matematikkolay.net 6k 3k 2k s(A B) 2.s(A B’) 3.s(B A’) s(A B) s(A B’) s(B A’) s(A B) 44 3k 2k 6k 44 11k 44 k 4 tür. 11 s(A) 3k 6k 9k 9.4 36 buluruz. 43 A ve B evrensel kümenin alt kümeleridir. s(E) 30 ve s(A’ B’) 12 ise A B kümesinin eleman sayısı kaçtır? www.matematikkolay.net ı ı ı ı ı ı ı ı ı ı Çözüm: Demorgan Kuralı A B A B A B A B Demorgan kuralına göre; s A B s A B 12 dir. s E s A B s A B dir. 30 s A B 12 30 12 s A B 18 s A B bulunur. 76 A ve B iki kümedir. s A B 2.s B A s A B 2.s A B s AUB 42 olduğuna göre s B kaçtır? s B A s A B 2.s B A s A B 2.s A B A B s A B 42 Ç özüm: x olsun. s(A B) 2x olur. s 4x olur. 42 2x 4x x 42 7x 42 x 6 dır. ise; s A B s A B s B 4x x 5x 05.Haz A s B s A B s B A 30 buluruz. 80 A ve B, E evrensel kümesinin iki alt kümesidir. s A’ B’ 6 s A’ B’ 32 s(A) s(B) 46 olduğuna göre, s(E) kaçtır? Çözüm: A’ B’ A B ‘ 6 A birleşim B dışında kalan eleman sayısı 6 imiş. A’ B’ A B ‘ 32 A kesişim B dışında kalan eleman sayısı 32 imiş. Bundan 6 çıkarırsak 26 buluruz. Sadece A ve Sadece B kümesine ait e lemanların sayısı 26 dır. s(A) s(B) 46 toplamında iki ker e kesişim kümeleri toplanır. Bundan 26’ yı çıkarırsak 20 buluruz. Kesişim kümesinin iki katı 20 ise s(A B) 10 dur. O halde; s(E) A B ‘ s(A B) 32 10 4 2 buluruz. 91 A ve B birer kümedir. s(A B) 12, s(B A) 2, s(A) 3.s(B) olduğuna göre; s(A B) kaçtır? www.matematikkolay.net Çözüm: s A B 12 Yalnız A ‘ ya ait s B A 2 Yalnız B’ ye ait S A B x olsun. s A 12 x s B 2 x olur. s A 3s B ise A’nın eleman sayısı B’nin eleman sayısının 3 katına eşit olur. B’nin 3 katı 3. 2 x 6 3x 12 x 6 3x 12 6 3x x 6 2x 6 x 3 bulunur. 2 92 s(A) 2.s(B), s(A B) 4, s(AB) 20 ise s(AB’) ? www.matematikkolay.net Çözüm: s A 2.s B ise s B x olsun. s A 2.x olur. s A B s A s B s A B 20 2x x 4 20 4 3x 24 3x 24 x 3 x 8 s A B’ s A B s A s A B s A 2.8 16 s A B s A s A B 16 4 12 93 A ve B kümeleri için s(B) 3 s(A B), s(A B) 9 ve s(A B) 45 tir. Buna göre s(B A) kaçtır? A) 26 B) 24 C) 16 D) 12 E) 8 www.matematikkolay.net x s(A B) 9 ve s(A B) x olacak şekilde küme şeklini yukarıda çizdik. s(B) 3 s(A B) soruda verilmiş s(B) 3x tir. B’nin tamamı 3x , A ile B’nin kesişimi x ise, B’nin A’dan farkı olan yer 2x olmalıd ır. s(B A) 2x tir. A birleşim B kümesinin toplamı 45 ise; 9 x 2x 45 9 3x 45 3x 36 x 12 dir. s(B A) 2x 2.12 24 buluruz. 95

