Soru Sor sayfası kullanılarak Kümeler konusu altında Alt küme soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU


5.SORU


6.SORU


7.SORU


8.SORU


9.SORU


10.SORU


11.SORU


12.SORU

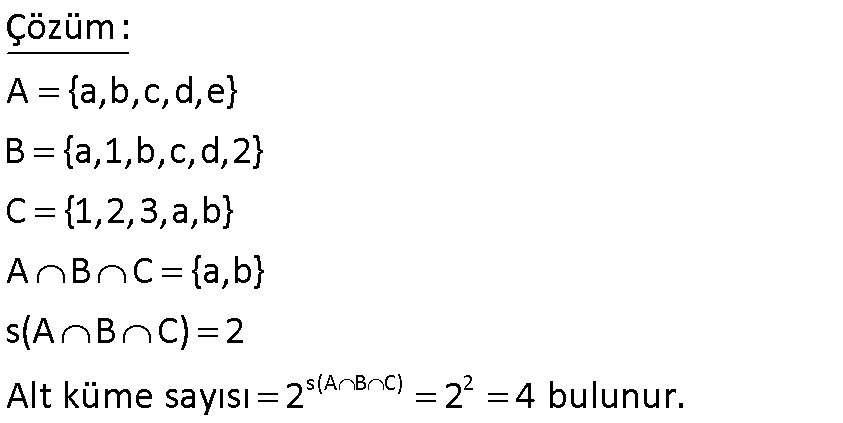
13.SORU


14.SORU

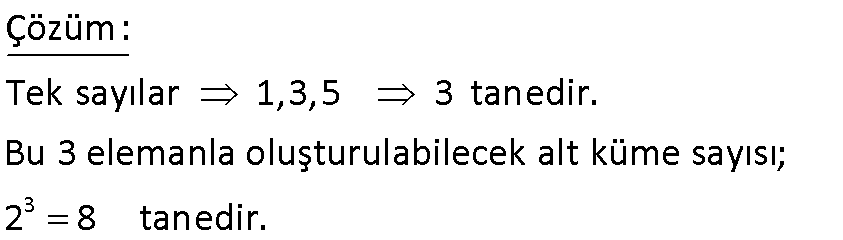
15.SORU


16.SORU


17.SORU


18.SORU
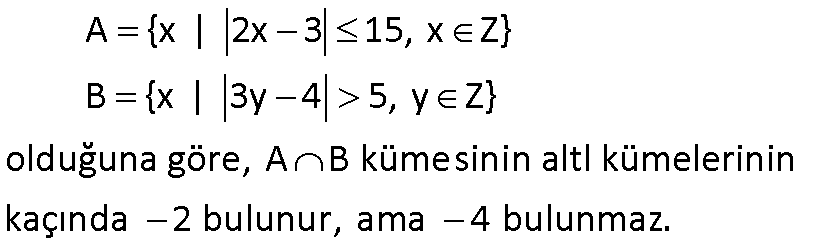

19.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
n Z olmak üzere, bir A kümesinin özalt küme sayısı 2n 1 dir. Bu kümeden 3 eleman çıkarılınca alt küme sayısı aşağıdakilerden hangisi olur? n n n n n A) B) C) D) E) 2 3 4 5 6 www.matematikkolay.net n n n n n 1 n 3 n 1 2 2 2 n Çözüm: Not :Özalt küme sayısı: 2 1 formülü ile bulunur. 2 1 2n 1 ise 2 2n 2 n 2 2 n dir. Kümeden 3 eleman çıkınca alt küme sayısı : n n 2 2 .2 n.2 buluruz. 2 4 8 A {1, 2, 3, 4, 5, 6} kümesinin, içinde 3 veya 4 ele – manlarından en çok birinin bulunacağı alt kümele – rinin sayısı kaçtır? A) 16 B) 20 C) 24 D) 32 E) 48 n 6 Çözüm: Alt kümelerinde ya 3 olacak, ya 4 olacak ya da ikisi de olmayacak. Yani biz, hem 3 hem de 4’ün bulunduğu alt kümeleri bulup, tümden çıkartırsak aynı sonucu buluruz. Tüm alt kümeler: 2 2 64 Hem 3,he n 2 4 m de 4’ün bulunduğu: 2 2 16 64 16 48 buluruz. 10 www.matematikkolay.net Bir kümenin eleman sayısı 2 arttırıldığında, alt küme sayısı 24 artmaktadır. Buna göre, ilk durumdaki kümenin eleman sayısı kaçtır ? A) 2 B) 3 C) 4 D) 5 E) 6 n n 2 n 2 n 2 n n n n n n n 3 Çözüm: n elemanlı bir kümenin alt küme sayısı 2 dir. Eleman sayısı 2 artınca alt küme sayısı 2 olacaktır. Buna göre; 2 2 24 eşitliğini kurabiliriz. 2 .2 2 24 4.2 2 24 3.2 24 2 8 2 2 n 3 buluruz. 14 A {a, b, c, d, e, f} kümesinin alt kümelerinin kaç tanesinde a ve b ele – manları birlikte bulunmaz? A) 8 B) 16 C) 32 D) 48 E) 64 www.matematikkolay.net 6 4 Çözüm: Tüm alt kümelerinden; a ve b’nin beraber bulunduğu alt kümeleri çıkartırsak sonucu buluruz. Tüm alt küme sayısı 2 64 a ve b’nin beraber bulunduğu alt küme sayısı: 2 16 Buna göre sorunun cevabını 64 16 48 buluruz. Doğru Cevap : D şıkkı 15 A {1, 2, 3, a, b, c} kümesinin alt kümelerinin kaç tanesinde a veya c den yalnız biri bulunur? A) 8 B) 16 C) 32 D) 64 E) 128 Çözüm: a’nın bulunup, c’nin bulunmadığı alt kümeler : A {1,2,3, a ,b, c 4 } 2 16 dır. c’nin bulunup, a’nın bulunmadığı alt kümeler : A {1,2,3, a 4 ,b, c } 2 16 dır. Soru bizden bu ikisinin toplamını istemektedir. 16 16 32 dir. www.matematikkolay.net 24 A 1,2,3,4,5,6,7,8,9,10 Yukarıda verilen A kümesinin en az iki elemanlı alt kümelerinden kaç tanesinin bütün elemanları ardışık tam sayılardan oluşur? www.matematikkolay.net Çözüm: 2 elemanlı ardışık alt kümelerine bakalım. 1,2 , 2,3 , 3,4 ,…, 9,10 9 tane 3 elemanlı ardışık alt kümelerine bakalım. 1,2,3 , 2,3,4 , 3,4,5 ,…, 8,9,10 8 tane 4 elemanlı ardışık alt kümelerine bakalım. 1,2,3, 4 , 2,3,4,5 ,…, 7,8,9,10 7 tane … 10 elemanlı ardışık alt kümelerine bakalım. 1,2,3,4,5,6,7,8,9,10 1 tane Yani bu şartlara uyan 09.Eki 1 2 3 … 9 45 alt küme vardır. 2 30 A C B olmak üzere s(A) 2 ve s(B) 6 ise bu koşullara uyan kaç tane C kümesi var dır? A) 7 B) 8 C) 12 D) 16 E) 24 www.matematikkolay.net 4 Çözüm: C kümesi, B kümesinin alt kümesidir ve elemanla rından 2 tanesi A kümesinin elemanlarıyla aynıdır. Buna göre; Diğer 4 eleman ile 2 16 alt küme yazılabilir. Cevap: 16 37 {1, 2, 3} A {1, 2, 3, 4, 5, 6, 7, 8} olduğuna göre, eleman olarak; 4’ün bulunduğu 5’in bulunmadığı kaç farklı A kümesi yazılabilir? A) 2 B) 4 C) 8 D) 16 E) 32 www.matematikkolay.net 3 Çözüm: A kümesinde 1,2,3 ve 4 elemanları bulunmak zorundadır. 5 elemanı da bulunmayacak. Geriye 6,7 ve 8 elemanları kaldı. Bu üç elemanla 2 8 alt küme yazılabildiğinden; 8 farklı A kümesi yazılabilir. 48 www.matematikkolay.net A 1,2,3,4,5,6 kümesinin, en az 2 elemanı ile yeni kümeler oluşturuluyor. Bu kümelerin tamamının elemanlarının toplamı kaçtır? A) 603 B) 612 C) 640 D) 651 E) 672 5 Çözüm: Örnek olarak “3” elemanının kaç ker e kullanıldığını bulalım. 3 elemanının bulunduğu alt küme sayısı 2 32 Sadece 3’ün bulunduğu {3} kümesini çıkarırsak; A kümesinin en az 2 elemanlı alt kümelerin de 31 kere 3 kullanıldığını buluruz. Bunun gibi diğer elemanlar da 31 ker e kullanılmış – tır. O halde toplamları; 31.(12 3 4 5 6) 31.21 651 buluruz. 54 A 1,2,3,4,5 kümesinin alt kümelerinin kaç tanesinde 1 elemanı bulunur? A) 4 B) 8 C) 12 D) 16 E) 24 4 Çözüm: Alt kümelerde “1” sürekli bulunacaksa, diğer 4 eleman ile farklı alt küme oluşturabiliriz. 4 eleman ile yapılabilecek alt küme sayısı 2 16 dır. 59 A {1,a,b,c,d} ve B {a,1,b,2,c,3} kümeleri veriliyor. Aşağıdakilerden hangisi A B kümesinin bir alt kümesi değildir? A) b,c B) 1,a,b C) a,b,c D) 1,a,c E) 1,d Çözüm: A {1,a,b,c,d} B {a,1,b,2,c,3} A B {a,b,c,1} dir. A B kümesinde d eleman olarak bulunmadığından {1,d} A B bulunur. 61 www.matematikkolay.net A {a,b,c,d,e} B {a,1,b,c,d,2} C {1,2,3,a,b} kümeleri veriliyor. A B C kümesinin alt küme sayısı kaçtır? A) 15 B) 8 C) 7 D) 4 E) 2 s(A B C) 2 Çözüm: A {a,b,c,d,e} B {a,1,b,c,d,2} C {1,2,3,a,b} A B C {a,b} s(A B C) 2 Alt küme sayısı 2 2 4 bulunur. 62 A 1,2,3,4,5,6,7 kümesinin alt kümelerinden kaç tanesinin elemanları çarpımı çifttir? A) 16 B) 24 C) 30 D) 60 E) 112 7 4 Çözüm: A kümesinin alt küme sayısı 2 128 dir. A kümesinin tek elemanları 1,3,5,7 4 tanedir. Sadece tek sayılardan oluşan alt küme sayısı; 2 16 dır. Bunun dışındakilerde mutlaka bir çift sayı buluna – cağından, çarpımları çifttir. O halde cevabı; 128 16 112 buluruz. www.matematikkolay.net 63 A 1,2,3,4,5 kümesinin alt kümelerinin kaçında çift sayılar bulunmaz? A)4 B)6 C)8 D)16 E)32 3 Çözüm: Tek sayılar 1,3,5 3 tanedir. Bu 3 elemanla oluşturulabilecek alt küme sayısı; 2 8 tanedir. 64 A ve B kümelerinin alt küme sayıları toplamı 320 dir. Kümelerin eleman sayıları yarıya indirilirse, oluşan yeni kümelerin alt küme sayılarının toplamı kaç olur? A) 16 B) 20 C) 24 D)28 E) 32 www.matematikkolay.net m n m n 256 64 64 256 m m 8 n n 6 A’nın eleman sayısı m olsun. B’nin eleman sayısı n olsun. A ve B’ nin alt kümeler toplamı Çözü 2 2 320 2 2 320 2 256 2 2 m 8 dir. 2 64 2 2 n 6 dır. A kümesinin eleman sayısını ya m n : r 4 3 8 ısı 4 2 6 B kümesinin eleman sayısının yarısı 3 2 2 2 16 8 24 bulunur. 65 a 12345 kümesinin alt kümelerinin kaç tanesinde 2 ve 4 bulunmaz 5 bulunur? Çözüm: A 1,2,3,4,5 kümesinin alt kümelerinde 2,4 bulunmasın dendiği için bu iki eleman kümede yok gibi davranmalıyız. 5 elemanı alt kümelerde bulunsun dendiği için bu elemanı tüm alt kümelere yerleştiriri z.Kalan elemanlarla alt küme hesabı yaparız. A 1, 2 ,3, 4 2 , 5 Alt küme sayısı 2 4 bulunur. 68 Sekiz elemanlı bir kümenin en az bir elemanlı kaç tane öz alt kümesi vardır? 8 Çözüm: 8 elemalı bir kümenin alt küme sayısı 2 256 dır. En az 1 elemanlı alt kümelerinin sayısı sorulmuş. Yani boş küme olmaması isteniyor. Boş küme 1 tanedir. Geriye kalanlar da bize cevabı verir : 256 1 25 5 buluruz. www.matematikkolay.net 89 A {x | 2x 3 15, x Z} B {x | 3y 4 5, y Z} olduğuna göre, A B kümesinin altl kümelerinin kaçında 2 bulunur, ama 4 bulunmaz. Çözüm: A kümesinin elemanlarını bulalım. 2x 3 15 15 2x 3 15 12 2x 18 6 x 9 dur. A { 6, 5, 4,…,8,9} B kümesinin elemanlarını bulalım. 3y 4 5 3y 4 5 3y 9 y 3 4,5,6,…. veya 3y 4 5 3y 4 Bulunmasın Bulunsun 5 3y 1 1 y …., 3, 2, 1 dir. 3 Bu iki kümenin kesişimi ise; A B { 6, 5, 4 , 3, 2 , 1,4,5,6,7,8,9} dur. Alt küme çeşitliliğini diğer elemanlar sağlar. 4 ve 2 dışında 10 elem 10 10 an vardır. O halde; 2 farklı alt küme yazılabilir. Cevap : 2 www.matematikkolay.net 90 www.matematikkolay.net A ve B boş olmayan iki küme ve A B E olmak üzere, s(B A’) s(A B) s(A’ B’) 3 2 5 eşitliği veriliyor. s(E) 30 olduğuna göre, A kümesinin alt küme sayısı kaçtır? A) 8 B) 16 C) 32 D) 64 E) 128 Çözüm: s(B A’) s(A B) s(A’ B’) k dersek 3 2 5 s(B A’) 3k s(B A) 3k s(A B) 2k s(A’ B’) 5k s(A B) 5k Soruda, A kümesinin B’nin alt kümesi olduğu verilmiş. Bu nedenle s(A B) 0 dır. Şimdi Evrensel kümeyi yaza 6 lım. s(E) s(A B) s(A B) s(B A) s(A B) 30 0 2k 3k 5k 30 10k k 3 tür. s(A) s(A B) s(A B) 0 2k 2.3 6 dır. A’nın alt küme sayısı 2 64 buluruz. 26

